高等数学几个知识点的教学经验体会

吴先兵

长江师范学院数学与统计学院 重庆 408100

1 无穷小量阶的应用新技巧

1.1 无穷小量阶的概念

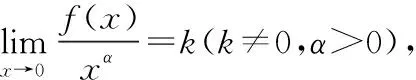
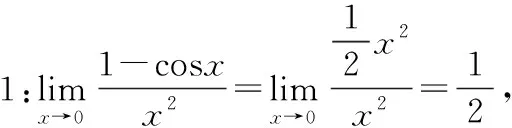
注：(1)显然xα(x→0)是α阶无穷小量。

(2)显然若f(x)-xα(α>0)，则f(x)是α阶无穷小量。

(3)f(x)是无穷小量，若f′(x)是α阶无穷小量，则f(x)是α+1阶无穷小量。

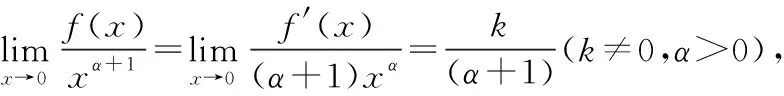
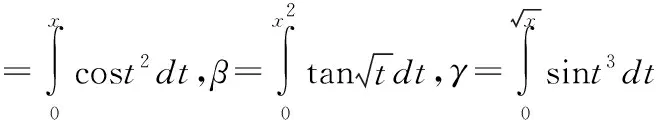
(A)α，β，γ(B)α，γ，β(C)β，α，γ(D)β，γ，α

分析：α′=cosx2=1(x→0+)，则α′是0阶无穷小量，因此α是一阶1无穷小量。

β′=2xtanx-2x2，则β′是2阶无穷小量，因此β是一阶3无穷小量。

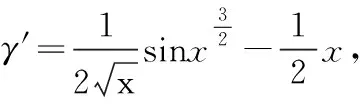
因此答案为(D)。

1.2 无穷小量的阶在极限计算的新技巧

大家都知道等价无穷小量替换计算极限适用于乘除形式，不适用于加减形式。

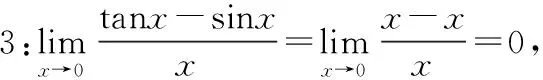
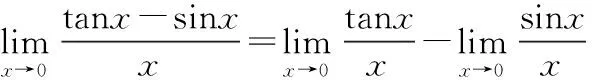
=1-1

=0

二者答案是一样的，但一个解题过程是错误的，一个解题过程是正确的。

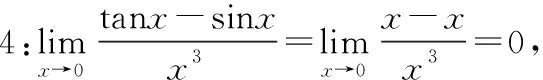
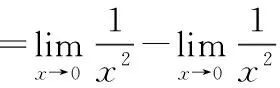
显然这个解法是错误的，因为不满足极限四则运算的前提条件“极限存在”。

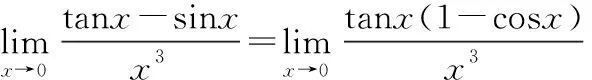
问题思考：以上两例在解法中，例3通过拆开的方法，转换成乘除形式利用等价无穷小量替换的解法是正确的；而例4通过拆开的方法，转换成乘除形式利用等价无穷小量替换的解法是错误的。原因何在？通过观察可以发现例3通过拆开的方法没有违背极限四则运算的前提条件“极限存在”，而例4通过拆开的方法违背了极限四则运算的前提条件“极限存在”。因此，只要拆开的方法没有违背极限四则运算的前提条件“极限存在”，就可以考虑拆开方法。事实上可以发现经验：只要拆开后，分子无穷小量的阶不小于分母分子无穷小量的阶就可以拆开。

下面提出新的技巧解题方法——配阶拆分法。

分析例4，分母是3阶无穷小量，故配3阶无穷小量。

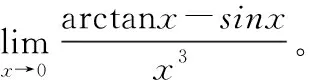
解题分析：因为分母是3阶无穷小量，故分子只要配出不低于3阶的无穷小量就可以拆分。

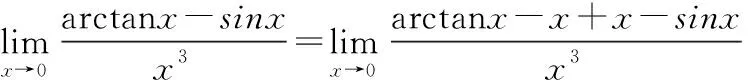
例6:(2009考研数二)求极限：

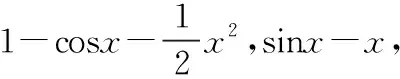
解：

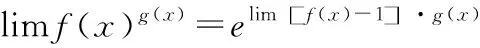
此时分母为4阶无穷小量，可通过洛必达法求导将分母为4阶无穷小量降为3阶无穷小量，再配阶分拆计算。

解：

例8：(2013考研数二)当x→0，时1-cosx·cos2x·cos3x与axn为等价无穷小，求n与a的值。

解题分析：axn为n阶无穷小量，故只要1-cosx·cos2x·cos3x知道是几阶无穷小量即可。

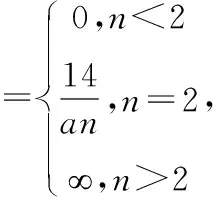
2 多元抽象复合函数求偏导经验

多元抽象函数求偏导是学生学习的一个难点，尤其求二阶偏导更难。在这里总结求多元抽象复合函数偏导规律的如下，便于学生们参考学习。

经验：(1)函数对第一位置的变量偏导乘以第一位置的变量(偏)导+函数对第二位置的变量偏导乘以第二位置的变量(偏)导+函数对第三位置的变量偏导乘以第三位置的变量(偏)导……

(2)抽象函数的偏导函数与原函数有相同变量构造，再次求偏导应重复(1)。

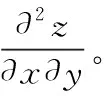
解题分析：该题主要考查多元抽象复合函数求导和全微分不变性，可用上面规律。

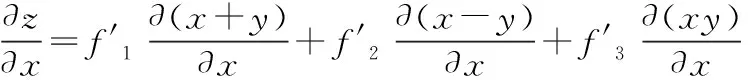
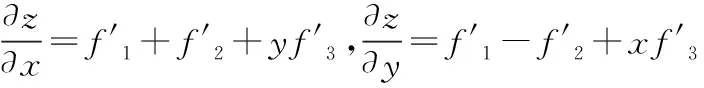
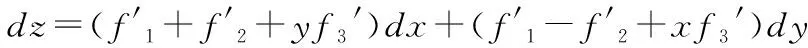
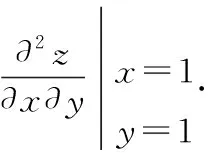
解题分析：该题主要考查多元抽象复合函数求导和极值问题。

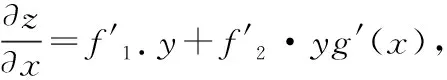
又函数g(x)可导且在x=1处取得极值g(1)=1.

所以，g′(1)=0，故：

3 多元隐函数求偏导经验

多元隐函数求偏导也是学生学习的一个难点，在这里总结求偏导规律如下：

经验：(1)一个方程只决定一个函数，两个方程决定两个函数，根据所求结果决定变量中哪些是函数变量，哪些是自变量。

(2)对方程两边某自变量求偏导时，其余自变量视为常量，注意函数变量一定不能视为常量，即函数变量一定是该自变量的函数。

经验运用举例：例11：(2004考研数一)设u=f(x，y，z)连续可偏导，且函数z=z(x，y)，由xex-yey=zez确定，求du。

解题分析：该题有两个方程，故有两个函数变量，共涉及四个变量x、y、z、u，根据题设，可确定z、u为函数变量，x、y为自变量。该题考查多元抽象函数求偏导和多元隐函数求偏导两个知识点，可考虑用上面两个规律来求解。

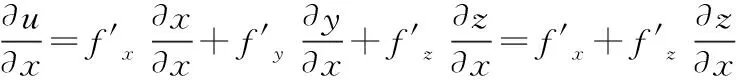
解：两个方程两边对x求偏导有:

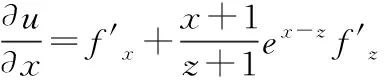
两个方程两边对y求偏导有：

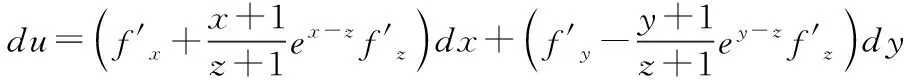
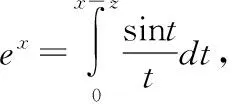
解题分析：该题有三个方程，故有三个函数变量，共涉及四个变量x、y、z、u，根据题设，可确定z、u、y为函数变量以及x为自变量。该题考查多元抽象函数求偏导和多元隐函数求偏导两个知识点，可考虑用上面两个规律来求解，该题还考查了变限积分函数求导方法。

解：对三个方程两边对x求导，有:

(1)

(2)

(3)

联立(1)(2)(3)解得: