采煤机螺旋滚筒装煤性能优化
李明昊,牛昊,范佳艺,赵丽娟,乔捷
(1.沈阳理工大学 机械工程学院,辽宁 沈阳 110159;2.沈阳航空航天大学 机电工程学院,辽宁 沈阳 110136;3.辽宁工程技术大学 机械工程学院,辽宁 阜新 123000;4.辽宁省大型工矿装备重点实验室,辽宁 阜新 123000)
0 引言
螺旋滚筒是采煤机破煤和装煤的直接机构,其装煤性能对采煤机工作效率有直接影响。如果螺旋滚筒破煤之后不能实现有效装煤,残留的浮煤落在采空区需人工清理,影响综采工作面生产效率,且受工作面气流影响,易形成浮煤飞扬,危害工作面人员身体健康,对工作面安全生产带来隐患。提高采煤机螺旋滚筒的装煤性能,最大程度地消除工作面安全隐患,是螺旋滚筒优化设计领域的重点研究课题。
目前,螺旋滚筒的优化设计主要采用有限元法和二维离散元法[1]。文献[2]针对薄煤层采煤机滚筒的装煤性能进行了分析,基于理论公式和二维离散元法得到螺旋滚筒不同设计变量对装煤性能的影响程度。文献[3]基于采煤机螺旋滚筒的装载机理和截割性能分析,得到螺旋滚筒优化设计变量对螺旋滚筒综合性能的影响程度,但未求出最优解,且设计变量不丰富。文献[4]针对井下特殊条件,研究了工作面倾角对采煤机滚筒装煤效果的影响,并得出定量化规律。文献[5]采用有限元法研究了异形滚筒的装煤性能和块煤率,通过多组仿真得到了筒毂锥顶半角的最优解。现有研究大多基于单一或部分因素对螺旋滚筒进行优化,未综合考虑螺旋滚筒设计变量对装煤性能的影响。而螺旋滚筒设计变量多,难以同时得到滚筒几何参数及运动学参数的最优解。针对该问题,本文基于煤的物理力学特性测试结果,建立了螺旋滚筒截割煤壁耦合模型;对采用不同设计变量时的螺旋滚筒模型进行装煤性能仿真,得到滚筒设计变量对装煤性能的影响规律;基于正交试验法设计螺旋滚筒的三因素三水平正交试验,得到螺旋滚筒最优几何参数和截割策略。
1 离散元数值模拟理论
1.1 煤颗粒接触模型
离散元法主要思想是将物体分成若干个离散体,通过设置离散体之间的接触模型[6]对其进行数值模拟分析。构建接触模型是离散元法的关键。
本文将煤颗粒设置为球体。假设2 个煤颗粒分别以速度v1,v2和角速度ω1,ω2运动并产生接触[7],接触模型如图1 所示。其中Fcn,Fct,Fdn,Fdt分别为煤颗粒之间的法向接触力、切向接触力、法向接触阻尼力、切向接触阻尼力,R1,R2为2 个煤颗粒的半径。

图1 煤颗粒接触模型Fig.1 Coal particles contact model
基于煤颗粒受力分析,结合常用的Hertz 接触模型,建立煤颗粒接触模型的力与位移关系式:

式中:F为煤颗粒之间的作用力;E*为煤颗粒之间的等效弹性模量;R*为煤颗粒之间的接触半径;ε为煤颗粒相互重叠值;U为煤颗粒之间的相对位移。
煤颗粒在破碎碰撞过程中的法向刚度kn、切向刚度ks分别为

式中:E为煤颗粒的弹性模量;μ为煤颗粒的泊松比;Fn为煤颗粒在破碎碰撞过程中的法向力。
1.2 煤颗粒运动学分析模型
螺旋滚筒通过截齿截割煤层,通过螺旋叶片装煤。建立被截落的煤颗粒与螺旋叶片之间的运动学分析模型[8-9],如图2 所示。其中Pt为落煤切向力,Px为轴向抛煤力,N为叶片对煤颗粒产生的正压力,β为螺旋叶片升角。

图2 煤颗粒运动学分析模型Fig.2 Kinematics analysis model of coal particles
对煤颗粒进行平衡受力分析,得
式中 α为叶片与煤颗粒之间的摩擦因数。
基于煤颗粒运动学分析理论,得到螺旋滚筒装煤功率:

式中vt为煤颗粒切向速度。

式中:m为滚筒转速;D1为煤颗粒所处位置与滚筒回转中心的距离;ρ为摩擦角。
基于式(7)可得
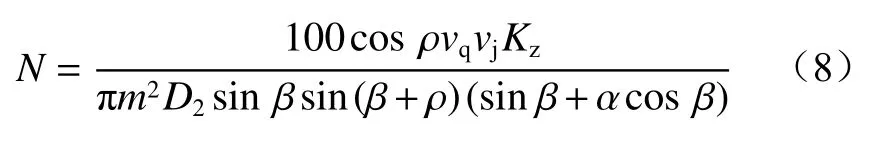
式中:vq为牵引速度;vj为 截齿截割的线速度;Kz为装煤阻力系数;D2为螺旋滚筒直径。
2 基于离散元的螺旋滚筒装煤性能分析
2.1 煤物理力学特性测试
选取切割机将煤样切割成标准试样,采用捣碎法、比重瓶和烘干法测试煤样的物理特性,如图3 所示。测得煤样密度为1 325.5 kg/m3,天然含水率为8.63%,孔隙率为9.53%,坚固性系数为2.0,弹性模量为4 388 MPa,泊松比为0.23。

图3 煤样物理特性测试Fig.3 Physical characteristics test of coal samples
选取电阻应变片和微机控制电子式万能试验机测试煤样的力学特性,如图4 所示。测得煤样抗拉强度为1.08 MPa,抗压强度为17.71 MPa。

图4 煤样力学特性测试Fig.4 Mechanical characteristic test of coal samples
2.2 滚筒截割煤壁耦合模型建立
基于煤样物理力学特性测试数据,采用离散元分析软件EDEM 建立煤壁。以MG400/950 型采煤机为研究对象,为使滚筒装煤性能最优且不堵塞叶片,选取2 头的TY1150 型顺序式排列螺旋滚筒,截割方式为抛射截割。建立螺旋滚筒截割煤壁耦合模型,如图5 所示。

图5 螺旋滚筒截割煤壁耦合模型Fig.5 Coupling model of screw drum cutting coal wall
2.3 装煤性能仿真
设置EDEM 仿真步长为0.1 s,仿真时间为10 s;采煤机牵引速度为4 m/min,滚筒转速为58 r/min。仿真得到的采煤机螺旋滚筒装煤效果如图6 所示。

图6 螺旋滚筒装煤效果仿真结果Fig.6 Simulation results of coal loading effect of screw drum
对采煤机螺旋滚筒装煤效果进行统计分析。将煤颗粒落在刮板输送机上的有效装煤区域定义为区域Ⅰ,落在刮板输送机以外的其他区域定义为区域Ⅱ,如图7 所示。则采煤机装煤率为落在区域Ⅰ的煤质量与截落的所有煤质量之比[10]。利用EDEM 后处理模块统计采煤机装煤率,可知该工况下装煤颗粒数为8 028,未成功装煤颗粒数为5 225,装煤率为60.57%。

图7 螺旋滚筒装煤效果统计Fig.7 Statistics of coal loading effect of screw drum
3 螺旋滚筒设计变量对装煤性能的影响分析
螺旋滚筒的螺旋升角、直径、筒毂直径、截割深度、转速和牵引速度是影响装煤效果的重要因素,其中滚筒直径影响螺旋叶片的几何形状,筒毂直径影响滚筒容煤量,螺旋升角影响滚筒截齿的位置和滚筒排煤效果[11]。将上述6 种参数选为螺旋滚筒设计变量,初始值分别为13°,1 150 mm,525 mm,800 mm,58 r/min,8 m/min。采用单因素法研究各变量对螺旋滚筒装煤性能的影响。
3.1 螺旋升角对装煤率的影响
设置螺旋升角分别为8,11,13,15,18°,其他设计变量均取初始值,计算采煤机装煤率,并对计算结果进行数据拟合,得到螺旋升角对装煤率的影响规律,如图8 所示。

图8 螺旋升角对采煤机装煤率的影响规律Fig.8 Influence law of spiral rising angle on coal loading rate of shearer
从图8 可看出,随着螺旋升角增大,装煤率增大,但后期增长速度减缓。这是因为随着螺旋升角增大,煤颗粒与螺旋叶片接触时速度得到提升,使较多的煤颗粒落在区域Ⅰ,提高了装煤率。当螺旋升角超过17°时,煤颗粒的法向速度和轴向速度产生临界值的改变,煤颗粒加速度降低,使得装煤率呈缓慢增长趋势。
3.2 螺旋滚筒直径对装煤率的影响
设置滚筒直径分别为1 050,1 100,1 150,1 200,1 300 mm,其他设计变量均取初始值,计算采煤机装煤率,并对分析结果进行数据拟合,得到滚筒直径对装煤率的影响规律,如图9 所示。

图9 滚筒直径对采煤机装煤率的影响规律Fig.9 Influence rule of drum diameter on coal loading rate of shearer
从图9 可看出,采煤机装煤率随滚筒直径增大而增大。这是因为滚筒直径增大时,采煤机容煤量增加,使螺旋叶片内的煤颗粒更多地落到区域I 上,提高了装煤率。
3.3 筒毂直径对装煤率的影响
设置筒毂直径分别为475,500,525,550,570 mm,其他设计变量均取初始值,计算采煤机装煤率,并对分析结果进行数据拟合,得到筒毂直径对装煤率的影响规律,如图10 所示。
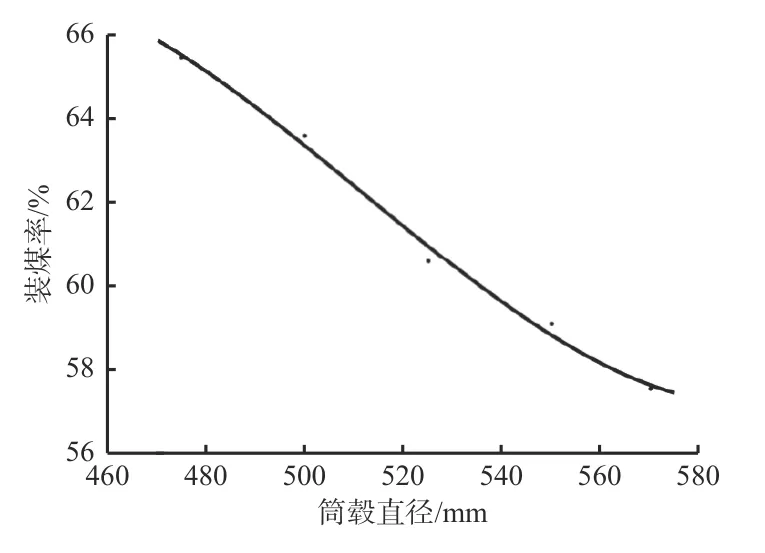
图10 筒毂直径对采煤机装煤率的影响规律Fig.10 Influence rule of hub diameter on coal loading rate of shearer
从图10 可看出,采煤机装煤率随筒毂直径增大而减小。这是因为随着筒毂直径增大,采煤机容煤量减小,不利于螺旋叶片内的煤颗粒落到区域I 上,降低了装煤率。
3.4 截割深度对装煤率的影响
设置截割深度分别为600,650,700,750,800 mm,其他设计变量均取初始值,计算采煤机装煤率,并对计算结果进行数据拟合,得到截割深度对装煤率的影响规律,如图11 所示。
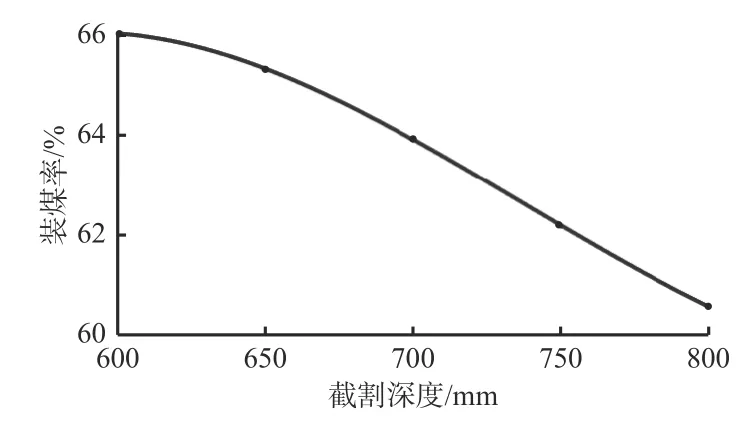
图11 截割深度对采煤机装煤率的影响规律Fig.11 Influence law of cutting depth on coal loading rate of shearer
从图11 可看出,随着截割深度增大,装煤率减小。这是因为截割深度增大时,开采深度增加,使得螺旋滚筒端盘处的煤颗粒不能及时经过螺旋叶片排出,落在区域Ⅱ,降低了装煤率。
3.5 滚筒转速对装煤率的影响
设置滚筒转速分别为50,54,58,62,66 r/min,其他设计变量均取初始值,计算采煤机装煤率,并对分析结果进行数据拟合,得到滚筒转速对装煤率的影响规律,如图12 所示。
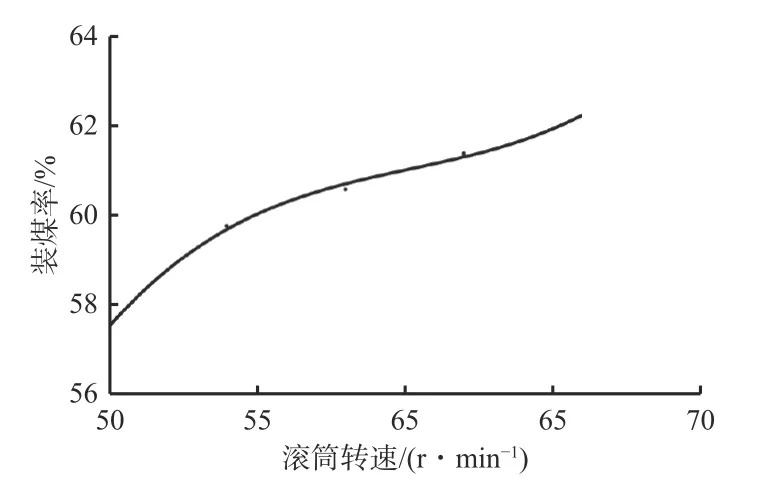
图12 滚筒转速对采煤机装煤率的影响规律Fig.12 Influence of drum rotation rate on coal loading rate of shearer
从图12 可看出,装煤率随滚筒转速提高而增大。这是因为随着滚筒转速增大,煤颗粒以更快的速度经螺旋叶片排出,提高了装煤率。
3.6 牵引速度对装煤率的影响
设置牵引速度为分别6,7,8,9,10 m/min,其他设计变量均取初始值,计算采煤机装煤率,并对计算结果进行数据拟合,得到牵引速度对装煤率的影响规律,如图13 所示。

图13 牵引速度对采煤机装煤率的影响规律Fig.13 Influence law of traction speed on coal loading rate of shearer
从图13 可看出,装煤率随牵引速度的提高呈先增大后减小的变化规律。这是因为牵引速度较小时,截割的煤颗粒较少,螺旋叶片内部容纳的煤颗粒因螺旋叶片内运动空间较大,向螺旋叶片边缘处运动,不能及时有效地经螺旋叶片排出。随着牵引速度增大,上述现象得到一定程度改善。但当牵引速度超过8 m/min 时,截割的煤颗粒超过滚筒容煤量,造成煤颗粒堵塞,降低了装煤率。
4 螺旋滚筒优化及截割策略研究
4.1 多因素分析
螺旋滚筒的单因素分析不能完全反映各设计变量对装煤性能的影响。正交试验法可分析螺旋滚筒多个设计变量在交互作用下对装煤性能的影响[12]。
4.1.1 正交试验设计
将螺旋升角、滚筒直径、筒毂直径、截割深度、滚筒转速、牵引速度6 种设计变量作为试验因素,分别定义为a,b,c,d,e,f。基于单因素分析结果,对6 种试验因素分别选取不同的水平,见表1。

表1 正交试验因素水平Table 1 Factor levels of orthogonal test
以螺旋升角、滚筒直径、筒毂直径作为几何因素,截割深度、滚筒转速、牵引速度作为运动学因素,按照L933正交表进行离散元模拟试验,结果见表2-表5。其中Xr为因素X(X=a,b,c,d,e,f)的第r(r=1,2,3)个水平值;L1,L2,L3分别为对应的因素水平为1,2,3 时的装煤率之和;l1,l2,l3分别为L1,L2,L3平均值。

表2 几何因素正交试验结果Table 2 Orthogonal test results of geometric factors
4.1.2 极差分析
极差反映了设计变量的波动性,通过极差分析可得到设计变量的影响程度。极差越大,表明该因素的影响程度越大[13]。由表3 可知,因素b,c,a的极差依次减小,表明几何因素对采煤机螺旋滚筒装煤性能的影响程度由大到小依次为滚筒直径、筒毂直径、螺旋升角。由表5 可知,因素d,e,f的极差依次减小,表明运动学因素对采煤机螺旋滚筒装煤性能的影响程度由大到小依次为截割深度、滚筒转速和牵引速度。
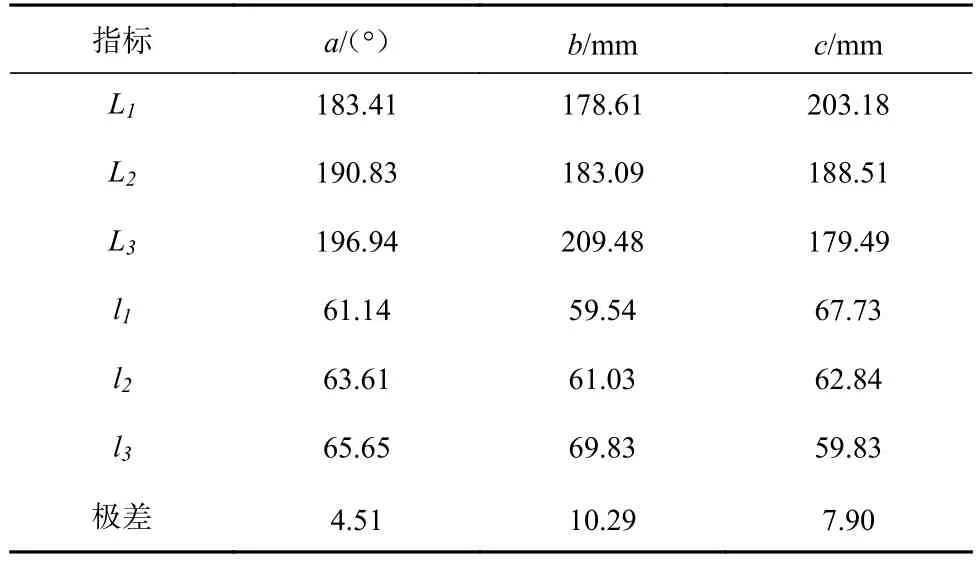
表3 几何因素极差分析Table 3 Range analysis of geometrical factors
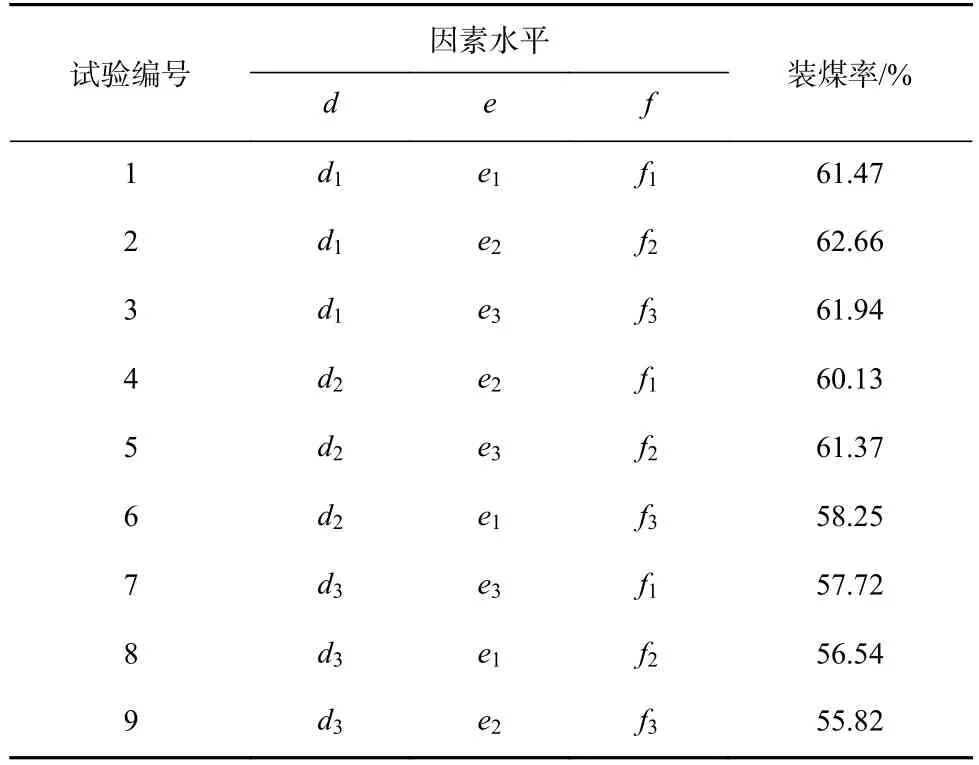
表4 运动学因素正交试验结果Table 4 Orthogonal test results of kinematic factors

表5 运动学因素极差分析Table 5 Range analysis of kinematic factors
4.2 螺旋滚筒优化及截割策略分析
由表2 和表3 可知,螺旋滚筒几何参数设计变量螺旋升角、滚筒直径和筒毂直径的最优水平分别为a2,b3,c1,因此几何参数最优设计方案为13°螺旋升角、1 300 mm 滚筒直径、475 mm 筒毂直径。该设计变量水平下采煤机装煤率为74.23%。
由表4 和表5 可知,螺旋滚筒运动学参数设计变量截割深度、滚筒转速和牵引速度的最优水平分别为d1,e2,f2,即最优截割策略为600 mm 截割深度、58 r/min 滚筒转速、8 m/min 牵引速度。该设计变量水平下采煤机装煤率为62.66%。
选取上述螺旋滚筒最优参数进行滚筒截割煤壁的EDEM 仿真,得到采煤机装煤率为76.39%,较优化前提高了15.82%。
5 结论
(1)基于煤的物理力学特性参数测试结果,采用离散元分析软件EDEM 构建了采煤机螺旋滚筒截割煤壁耦合模型,仿真得到螺旋滚筒截割煤层时的装煤性能数据。
(2)基于离散元分析结果,利用单因素法分析了螺旋滚筒几何参数和运动学参数对截割性能的影响。利用正交试验法设计了螺旋滚筒三因素三水平正交试验,通过极差分析得出几何参数中滚筒直径、筒毂直径、螺旋升角对采煤机螺旋滚筒装煤性能的影响依次减小,运动学参数中截割深度、滚筒转速、牵引速度对螺旋滚筒装煤性能的影响依次减小。
(3)基于正交试验分析结果,得到螺旋滚筒最优几何参数方案为13°螺旋升角、1 300 mm 滚筒直径、475 mm 筒毂直径,最优截割策略为600 mm 截割深度、58 r/min 滚筒转速、8 m/min 牵引速度。优化后的采煤机装煤率为76.39%,较优化前提高了15.82%。

