基于星凸形随机超曲面的概率数据关联滤波器*

刘乐文

（兰州理工大学电气工程与信息工程学院 兰州 730050）

1 引言

在传统目标跟踪技术中，早期由于传感器分辨率的限制，通常只能用点来描述目标，即目标每一时刻最多只能生成一个量测，只能对目标的质心位置、速度、加速度等进行估计。随着现代传感器技术发展，高分辨率传感器在工程中的应用越来越广泛，导致每个时刻可以得到不止一个量测［1～3］，而扩展目标跟踪技术正是利用获得的多个量测信息，通过信息融合运算，得到对目标形状和运动状态的估计。

近些年扩展目标跟踪问题得到了广泛的关注，而对扩展目标形状进行估计是学者们研究的重点，因此，诞生了许多对扩展目标形状建模的方法。例如Baum等将扩展目标建模为随机超曲面模型（Random Hypersurface Model，RHM），该模型的核心思想是假设目标的量测源分布在目标边界的一个缩小版本之上，量测由处于缩小版本边界上的量测源和传感器噪声共同构成。星凸随机超曲面模型主要将径向函数用傅里叶级数展开从而描述目标轮廓，由展开系数实现对扩展目标形状建模，并结合尺度因子缩放扩展目标的形状完成对其表面量测源的建模［4～6］。随机超曲面模型假设目标产生的每一量测由对应的量测源产生，这种建模方式弊端会造成量测方程具有较强的非线性，为了解决这个问题，论文选择用容积卡尔曼滤波（Cubature Kalman Filter，CKF）算法对非线性伪量测方程的进行线性化处理。

由于存在杂波，并且扩展目标在每个时刻会产生若干个量测，这使得在扩展目标跟踪问题中，量测簇与目标的对应关系很难匹配。为了解决该问题，本文算法利用Bar-Shalom等提出了概率数据关联（PDA）算法计算量测与目标的关联概率，该算法核心思想是认为在观测区域中的有效量测都有可能源自目标，只是每个量测源自目标的概率不同，将各自概率进行加权平均作为滤波的输出结果［7～9］。

论文主要针对杂波环境下单扩展目标跟踪问题，将点目标下PDA思想推广到单扩展目标之中，提出了适用于杂波环境下的基于星凸随机超曲面模型的单扩展目标跟踪滤波器ET-SRHM-PDAF，该算法利用星凸形随机超曲面模型对量测进行建模，然后给出了ET-SRHM-PDAF中量测似然、关联概率等参数的详细推导过程。在评价指标的选择上，论文利用均方根误差（RMSE）和拟Jaccard距离，误差距离能够直观地反映出跟踪效果，RMSE对应扩展目标的质心位置，拟Jaccard距离对应形状轮廓。论文由对不同形状扩展目标（十字架形和五角星形）的跟踪仿真实验验证了该算法的可行性。

2 星凸形随机超曲面模型

首先介绍随机超曲面模型的定义［10～11］，假定为从尺度因子Ki的随机抽取值，其中Ki为一维随机变量，当量测源Si落在目标轮廓Pi向目标质心收缩Pj的曲面上，那么量测源可表达式可记为

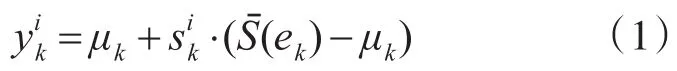
其中，Xi表示质心位置，Mθ(k)表示目标形状参数。

一般而言构建了随机超曲面模型和传感器量测模型后，可以建立起形状参数与量测之间的关系，这为本文研究的星凸形扩展目标的轮廓估计提供了依据。

由星凸形随机超曲面的定义可知，假设S为扩展目标内所有点构成的集合，记集合中任意一点与质心的连线为线段g。若线段g上全部点依然在集合S中，即称该跟踪目标是星凸形［12～14］。星凸形随机超曲面模型示意图如图1所示。

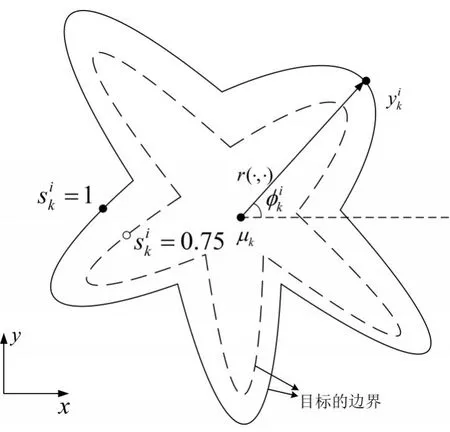
图1 星凸形随机超曲面模型示意图

假设星凸形扩展目标的边界用表示，则星凸形扩展目标的轮廓A(Mθ(k))可用径向函数来表示。径向函数记为K(Mθ(k))，定义为在已知角度时质心与边界点之间的距离。

当扩展目标形状不规则程度较高时［15～16］，为了得到较为简洁的径向函数的表达式，利用傅里叶级数将径向函数展开有

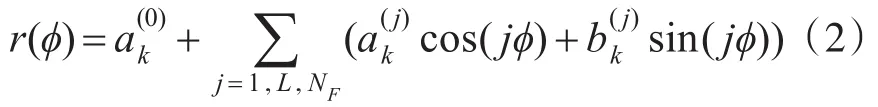
若角度ϕ固定，则式（2）可改写为

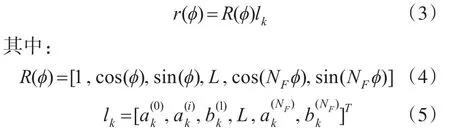
傅里叶级数展开的阶级越高，目标形状的轮廓细节则越具体。传感器量测模型表达式为

由上式可得量测方程为

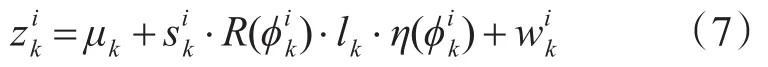
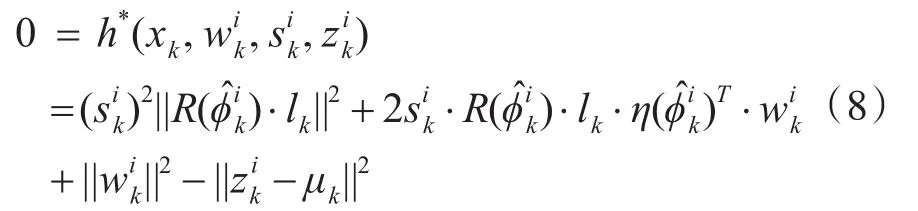
从式（8）可以看出，h*(·)建立了扩展目标状态、量测噪声和尺度因子与量测之间的关系，因此，将h*(·)称为伪量测函数。

3 星凸随机超曲面模型概率数据关联滤波器

3.1 概率数据关联算法

状态在时间上的条件均值可以写成：

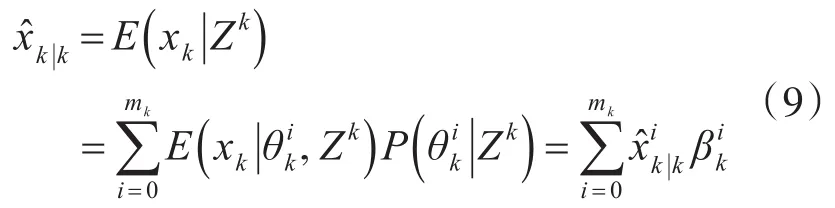
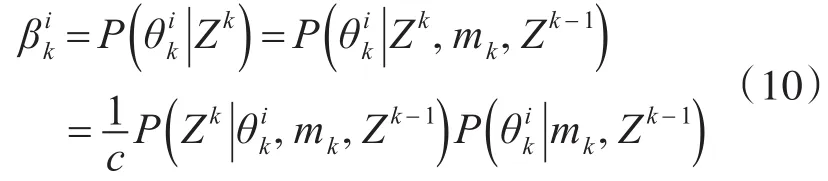
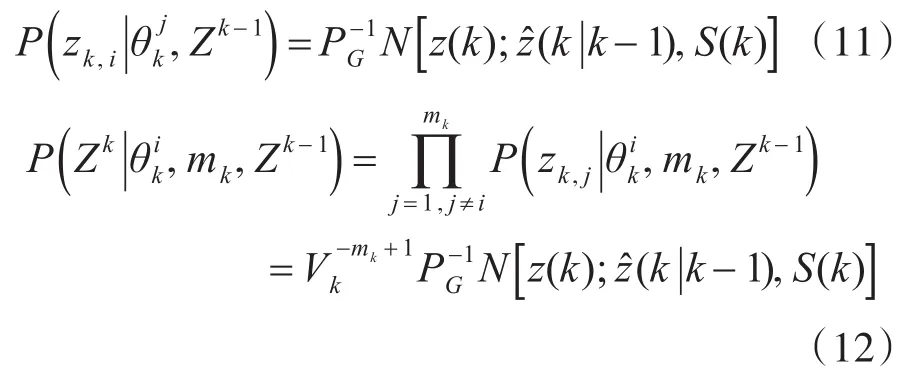
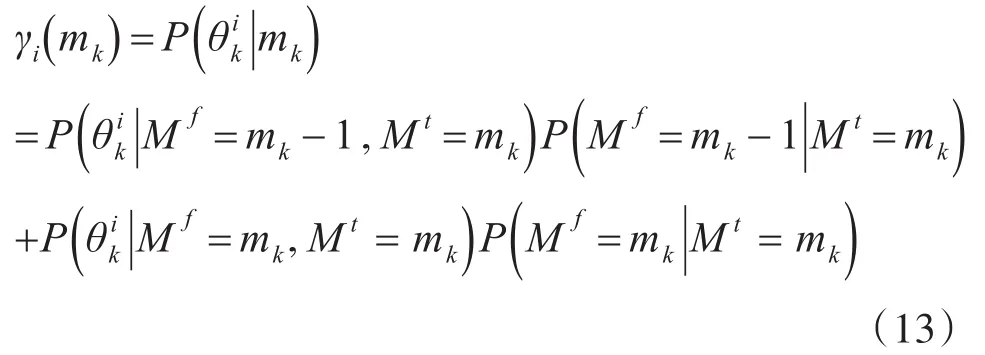
要计算γi(mk)，分为i=0和i=1，…，mk两种情况，即

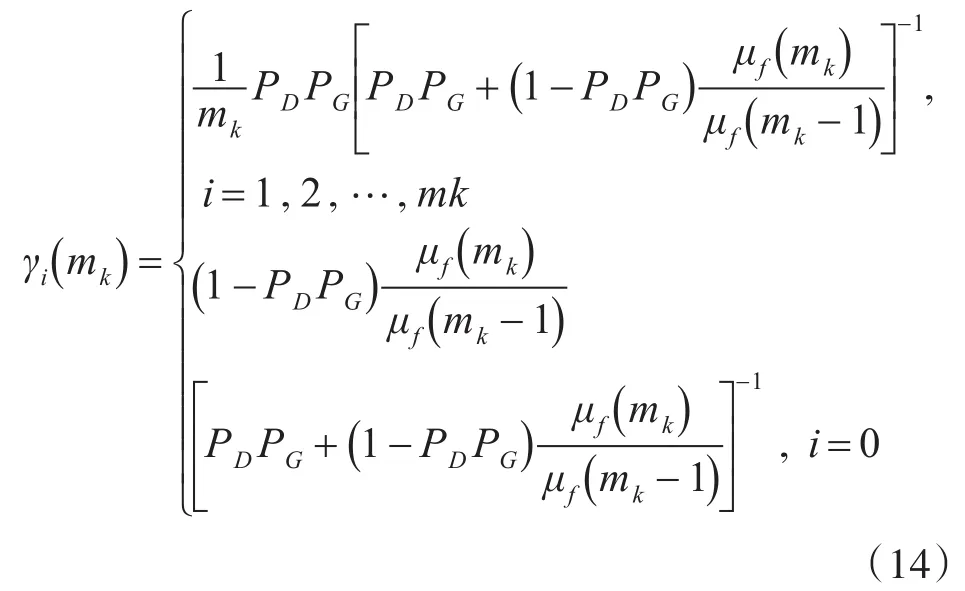
其中μf为杂波数目的概率密度函数，即

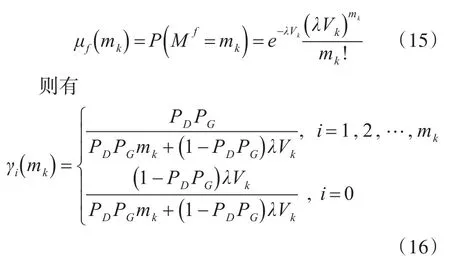
可计算关联概率为

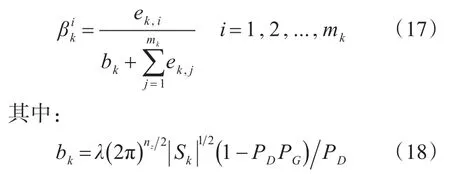
对目标状态进行估计：

Kk为Kalman增益矩阵，其中：

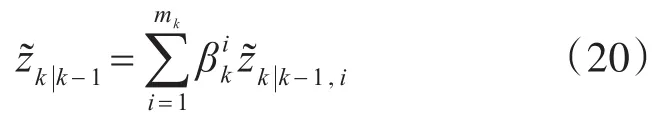
相应地的目标状态估计协方差为

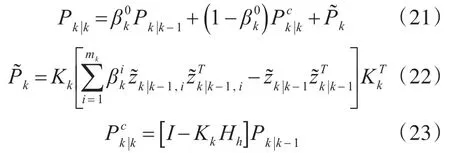
3.2ET-SRHM-PDAF跟踪算法

假定在第k个时刻，用星凸随机超曲面模型对目标进行建模，目标状态向量表示为

其中xk表示目标质心运动状态（包括目标质心位置、速度、加速度等）。

1）预测步

k+1时刻预测状态，预测协方差为

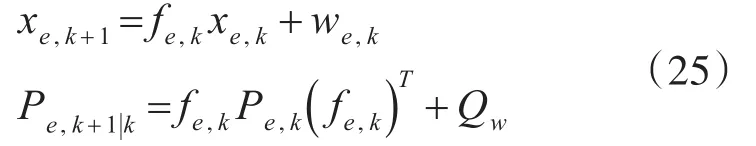
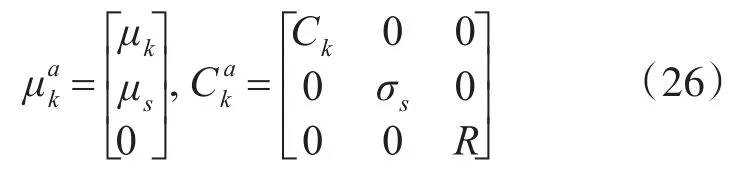
其中，μk和Ck分别表示目标质心运动的均值及协方差。

2）计算扩展目标关联概率

k+1时刻的关联事件的关联概率在星凸形随机超曲面模型中表达式为

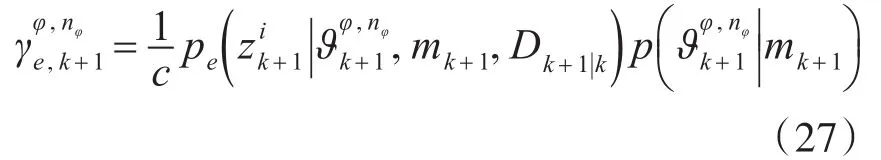
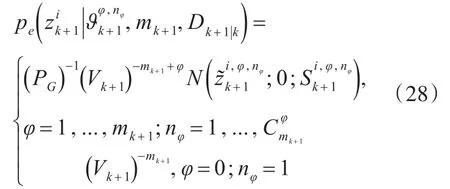
式（9）将状态向量xe，k，尺度因子，量测噪声和量测映射到伪量测函数0，其中为新息，。

即扩展目标关联概率可以表示为

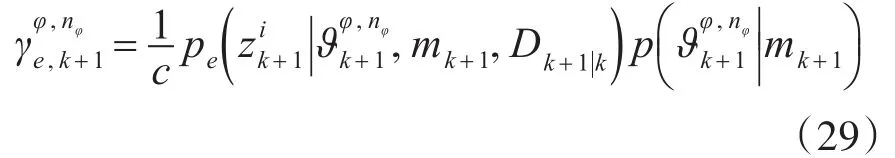
3）更新步

融合后的扩展目标状态估计和协方差估计表达式为

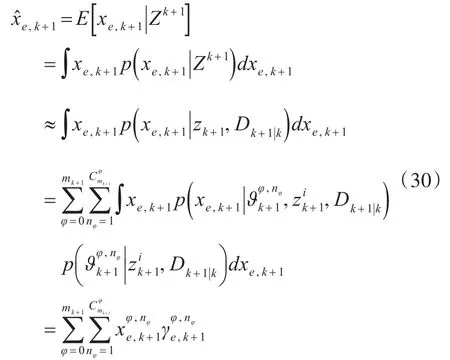
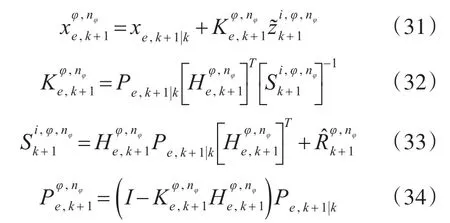
状态估计的协方差如下：

4 仿真分析

仿真设计构造两种不同形状（十字架形和五角星形）且做CV运动（匀速直线运动）的星凸形扩展目标，用本文提出的ET-SRHM-PDA算法和EKF-ET-PDA算法对目标进行跟踪仿真实验，然后对比两种算法分别对不同形状扩展目标的跟踪效果。

仿真场景设置在带有杂波环境的观测区域[0，1700]m×[-200，1100]m内存在单个做匀速直线运动的不规则扩展目标，总检测时间为20s，采样间隔为T=1S，探测概率PD=1.00，门概率PG=0.99。二维观测场景下初始运动状态为x0=[80m 80m/s 80m 40m/s]。

扩展目标每个时刻产生的量测数目服从参数为λm=20的泊松分布，系统杂波在观测区域内服从均匀分布，且个数根据均值为5的泊松分布随机生成。

ET-SRHM-PDA算法对十字架形状目标跟踪效果图如下图所示。

由仿真结果分析，图2是两种算法对十字架形状扩展目标的跟踪轨迹图，从中可以看出，在杂波环境下，两种算法对目标位置的滤波结果与真实轨迹的大致趋势是一致的。图3是在第11个时刻目标十字架形状估计结果的放大图，可以看出本文算法估计的轮廓更为贴近目标。

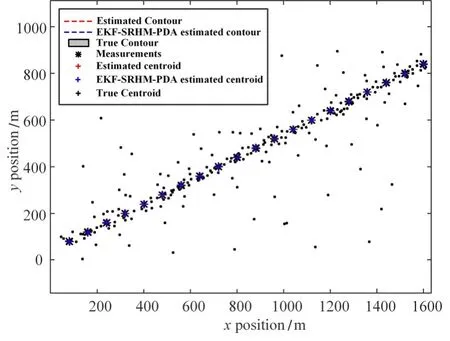
图2 十字架形跟踪轨迹图

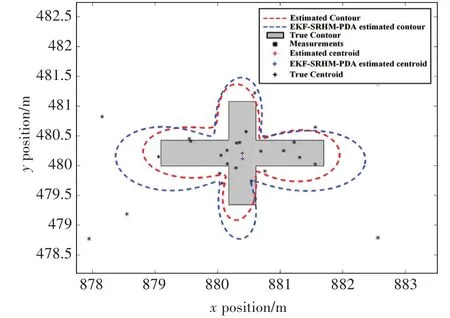
图3 K=11时刻十字架形跟踪局部放大图

图4和图5给出了两种算法质心位置估计的RMSE和形状估计的拟Jaccard距离，可以看出之心误差大致在0.1m左右，拟Jaccard距离本文算法更小。

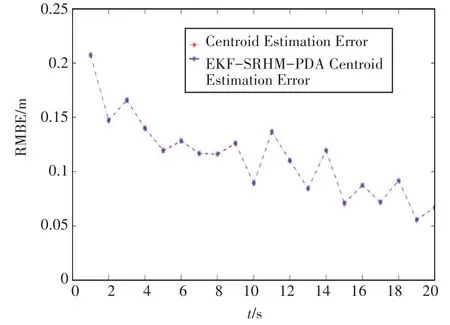
图4 十字架形质心估计RMSE误差图

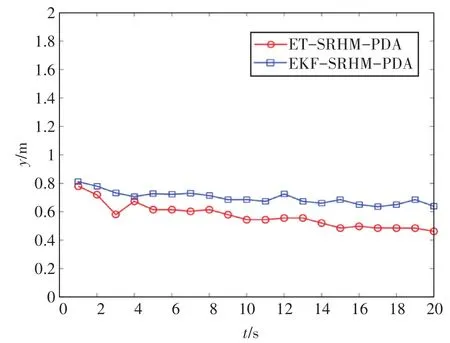
图5 十字架形拟Jaccard距离图

ET-SRHM-PDA算法对五角星形状目标跟踪效果图如图6～7所示。

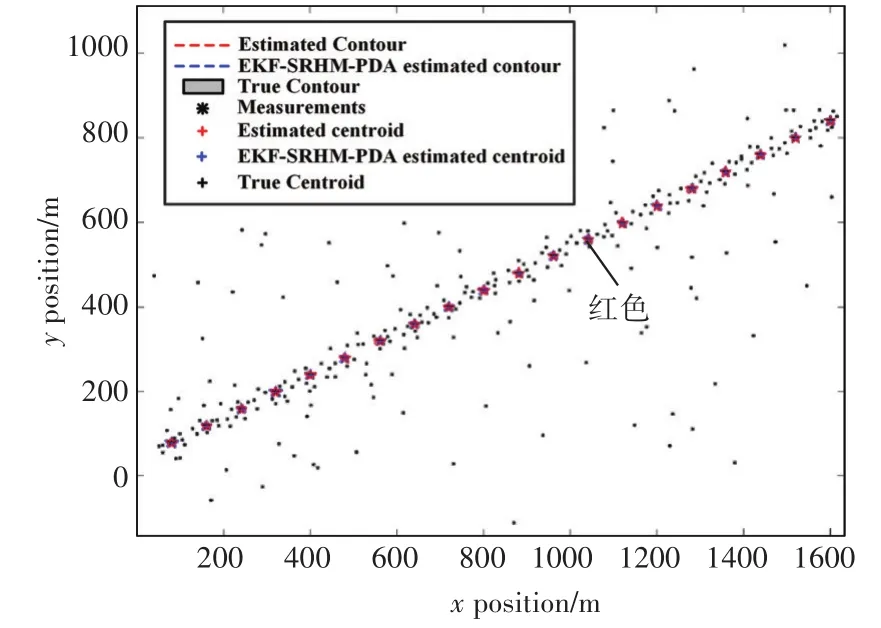
图6 五角星形跟踪轨迹图

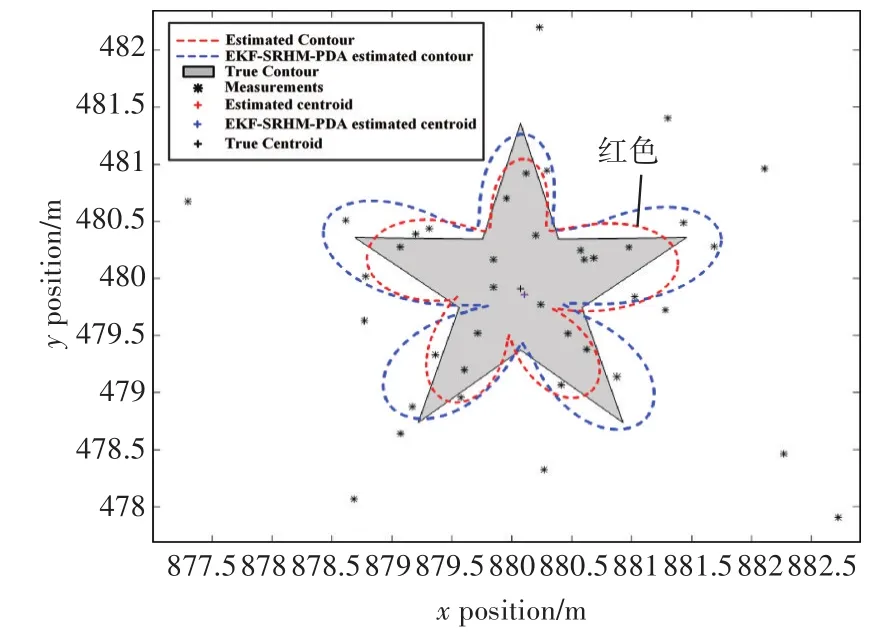
图7 K=11时刻五角星形跟踪局部放大图

图6和图7分别是两种算法对五角星形状扩展目标的跟踪轨迹图和局部放大图，从中可以看出，在杂波环境下，两种算法对目标位置的滤波结果与真实轨迹的大致趋势是一致的，本文算法红色轮廓更为贴近目标。

从图8和图9看出，质心估计两种算法误差接近，拟Jaccard距离本文ET-SRHM-PDA算法更小，说明本文算法对目标形状估计比已有算法更为精确。

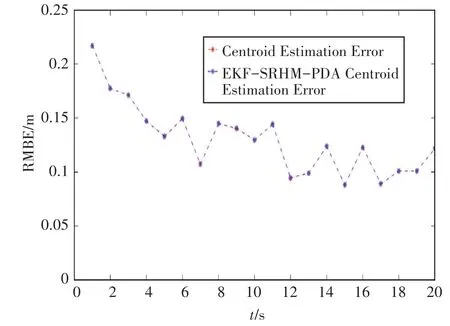
图8 五角星形质心估计RMSE误差图

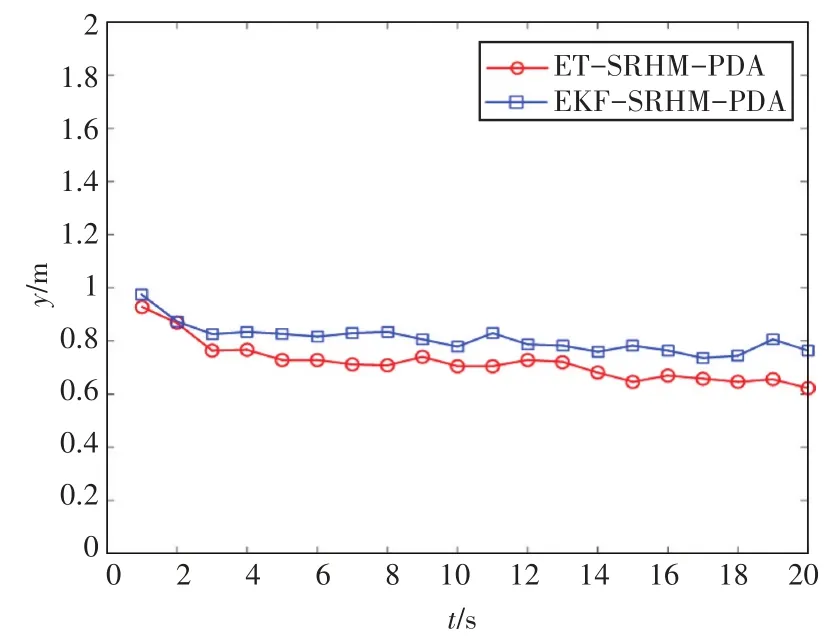
图9 五角星形拟Jaccard距离图

5 结语

本文针对杂波环境下不规则形状单扩展目标的跟踪问题，对RHM模型以及星凸形RHM模型进行了详细的介绍，其次对点目标概率数据关联算法进行了详细的推导，然后基于星凸形RHM，将点目标PDA算法推广到扩展目标的概率数据关联跟踪算法。最后，构造了两种形状的星凸形扩展目标跟踪仿真，通过与已有算法比较，本文算法不论是在目标的运动状态还是形状估计结果上都更为精确。