基于改进A*算法的无人机目标跟踪研究*

张 鑫

（商洛学院电子信息与电气工程学院 商洛 726000）

1 引言

无人机（Unmanned Aerial Vehicle，UAV）是一种不搭载操作人员能够自主飞行或进行远程引导的航空器。针对无人机目标跟踪问题，国内外有较多研究。文献［1］针对部队转移掩护任务研究无人机跟踪转移部队的方法，该研究假设部队位置实时发送给无人机，即目标为合作目标，因此，无人机所要考虑的问题是如何保持指定距离跟踪转移部队。文献［2］把目标的状态估计引入到平台的运动控制策略中进行考虑，在对移动目标跟踪的同时，估计运动目标的状态，然后采用Lyapunov控制方法保持传感器对目标的持续覆盖。但这两种方法并没有充分考虑无人机的动力学约束。

本文考虑的是对地面/海面机动目标的视觉跟踪，这需要对机载摄像机拍摄的图像进行处理，识别目标并计算目标的参数信息。利用改进A*算法和文献［3］的跟踪算法进行了目标跟踪，通过仿真，验证了改进A*算法的可靠性。

2 无人机机动模型

机动目标的模型有很多，其中协同转弯模型［4］和“当前”统计模型［5］是两种目前最常用的机动目标运动模型，下面分别对这两种模型进行介绍。

1）协同转弯模型

设运动目标的状态方程为

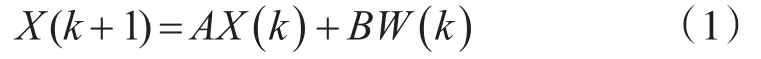
式中：A为状态转移矩阵；X(k)为目标状态矢量，X(k)=[x(k)(k)y(k)(k)]T，x、y表示目标位置；B为噪声驱动矩阵；W为服从N(0，Q)的高斯白噪声，Q为协方差矩阵。

对于转移矩阵A及噪声驱动矩阵B分别有：

式中：T为采样时间/s；ω为运动角速度/（rad/s），代表机动情况的参数，ω＞0表示左转弯，ω＜0表示右转弯，ω=0则表示匀速直线运动。

2）“当前”统计模型

设目标运动的状态方程为

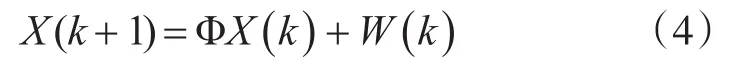
式中：X(k)为目标状态矢量，X(k)=[x(k)(k)(k)y(k)(k)(k)]T；Φ为状态转移矩阵；W(k)为白噪声序列，均值为0，方差为Q(k)。

对于状态转移矩阵Φ及白噪声序列方差Q(k)有：

式中：α为目标的机动频率。

3 航迹点规划方法

为了方便计算机解析，用航路点序列代替航路曲线［6～7］。无人机在固定高度定速飞行时，飞行轨迹从三维变为二维。图1表示此时的航迹点。

如图1所示，假设在t时刻，无人机所处位置为O，最大偏航角速率为ψ̇max。假设相邻航迹点的时间间隔为Δt，每个点有3种可能，则在3Δt内航路就有27种可能［8］。

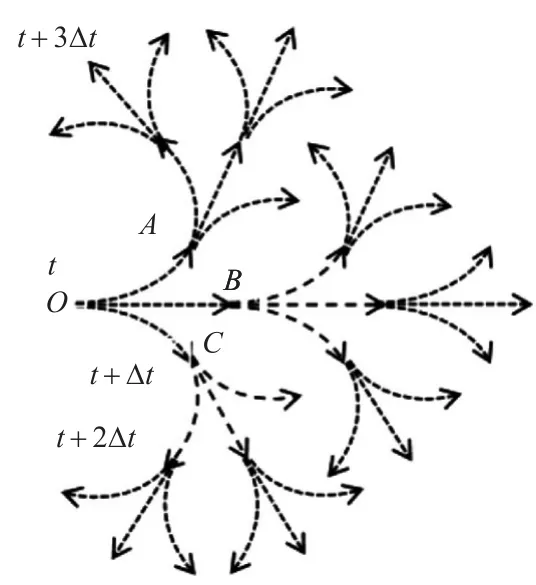
图1 航迹点扩展图

设无人机航迹点为(x，y，ψ)，其中x，y表示二维平面位置，ψ表示偏航角。假设t时刻航迹点O为(x0，y0，ψ0)，取Δt=1，那么航迹点A的状态信息为(x0-Rsinψ1+Rsinψ0，y0+Rcosψ1-Rcosψ0，ψ1)，其中ψ1=ψ0-ψ̇Δt，R=V/ψ̇为无人机转弯半径，V为无人机的速度。同理，其他的扩展节点信息可以依次求得。

根据模型预测控制思想，航迹点的规划步骤如下：

1）当前t0时刻，以Δt为步长，规划以后N步最优航迹点序列；

2）实际航迹点用前K步规划的点代替，其中0＜K＜N；

3）t0+KΔt时继续进行1）、2），直到任务终止。

目标跟踪流程图如图2所示。

图2 目标跟踪流程图

步骤1）中需要获得最优的航迹点序列。若无人机在每个位置上都有M个可以选择的航向，规划N步，则会有MN条不同航路可供选择。步骤1）的任务就是在MN条路中找到最优的航路。和TSP问题的求解类似，基于对实时性的考虑，选择A*算法，该算法效率高、运行速度快。

4 改进A*算法求解航迹点序列

A*算法是一种启发式的最优搜索算法。评价函数定义为

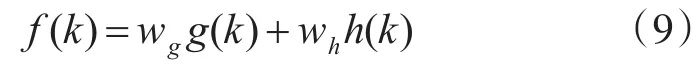
式中：f(k)为从起始节点经过点k到目标节点的代价估计值；wg为真实代价的加权；g(k)为从起始节点到当前节点k的真实代价；wh为估计代价的加权；h(k)为从当前节点k到目标位置的代价估计值。

图3 A*算法流程图

若UAV在每个位置上都有M个可以选择的航向，规划N步，则扩展的航迹点共有∑Mi(1≤i≤N)个。设每个航迹点编码为[mn]，其中m(1≤m≤N)表示扩展的第m步，n(1≤n≤Mm)表示第m步的第n个扩展节点。求最优航迹时将相应的航迹点编码加入Openlist、Closelist，只求出需要的航迹点的状态信息(x，y，ψ)。

A*算法［9］中的评价函数f(k)中包括消耗代价g(k)和估计代价h(k)。无危胁情况下，无人机在进行目标跟踪时，可以使g(k)=0。h(k)用来选择恰当的寻优方向，又被叫做启发函数［10］。因此，算法的可靠性和快速收敛性主要取决于h(k)。文献［3］直接将目标点与当前点间的欧氏距离看作h(k)，对于目标跟踪的问题，h(k)设为

式中：ρi为航迹点序列中第i个航迹点与目标水平方向的距离；ρd为UAV与目标的水平期望距离。

但是随着迭代次数的增加，采用上式会使以后增加的节点代价值增大，算法无法快速收敛。因此，根据文献［11～12］设置h(k)为

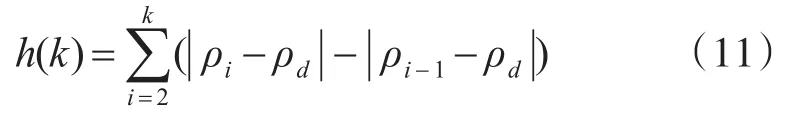
5 无威胁环境下目标跟踪仿真

设定无人机的最大偏航角速度ψ̇max为0.2rad/s，速度是50m/s，飞行的高度1000m，北东地坐标系下的起始坐标为（0，0，-1000）。

跟踪目标参数：静止，北东地坐标系下坐标为（2000，2000，0）。

任务要求：UAV与目标水平方向的期望距离ρd=500m。无人机先飞向目标附近，距离为期望距离时再盘旋飞行。

航路规划算法相关参数设置如下：步长为1s，每次预规划3步，实际执行1步，每个航迹点有9个航向可以选择。分别对静止目标和机动目标进行跟踪。

采用改进A*算法进行仿真，并与文献［3］算法的仿真结果进行比较，对静止目标的跟踪结果如图4所示，对机动目标的跟踪结果如图5和图6所示。文献［3］的跟踪结果用虚线，改进A*算法的结果用实线表示。图4中，黑点表示静止实物，图5、6中，粗线表示机动目标。

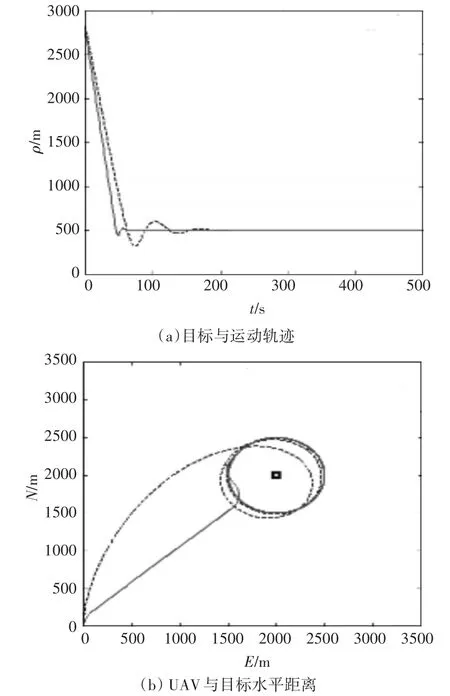
图4 静止目标的跟踪结果

图5 协调转弯模型下跟踪结果

图6 “当前”统计模型下跟踪结果

从图4中可以看出，两种算法都可以满足任务要求，但是本文算法比文献［3］能够更快地收敛至500m，且震荡较小，跟踪效果更优。

图5、6为协调转弯模型和“当前”统计模型下对机动目标的跟踪结果。由跟踪结果可知，本文算法与文献［3］中的算法相比收敛到期望距离的速度更快，并且目标产生了较大的机动时本文算法也能完成跟踪任务，偏差明显小于文献［3］中算法。

6 结语

首先分析了无人机的协同转弯模型和“当前”统计模型，在无危胁条件下，利用文献［5］的改进A*算法和文献［3］分别对静止目标和机动目标进行了跟踪，并进行了仿真对比。对比了两种算法下的目标轨迹与UVA运动轨迹，UVA与目标的水平距离。仿真结果表明，改进A*算法能有效地实现目标跟踪。