多视角探究一道以梯形为背景的解三角形问题

广东省佛山市顺德区第一中学 (528300) 常 艳

求解解三角形问题时，常常使用正、余弦定理进行求解，其本质是将三角形中的图形信息代数化，通过方程的思想进行求解.而三角形本身具有丰富的几何性质，也是体现数形结合思想的理想素材.2021年佛山市一模第18题便是一道优质的解三角形问题，该问题背景丰富，解题角度多，本文将从多个角度对该问题进行分析，并探寻其命制原理与背景.

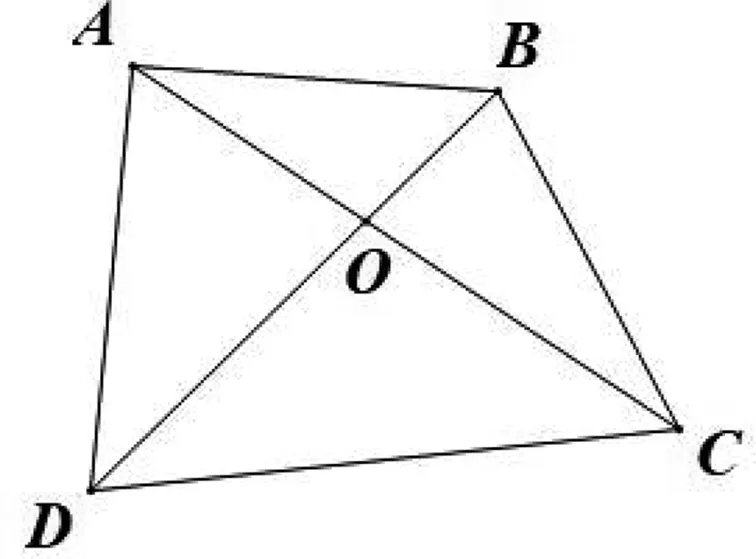
一、题目

本题以“梯形”为背景，蕴含丰富的数量关系与几何关系.本题的第(1)问给出的信息较为完整，可以完整地确定出所有的边长及角度信息；而第(2)问给出了对角线的夹角关系(垂直)，自然将解题的视角聚焦在内部的小三角形上.以下的解答过程只分析第(2)问.

二、解法呈现

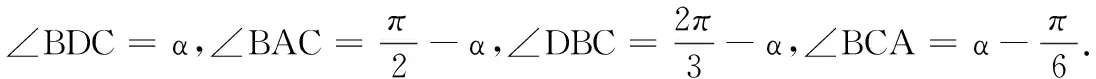
图2

解法三：(正切关系)由解法一可知，该“梯形”完全可解，但为何会选择问一个角的“正切”值呢？而上两种解法有一种“围魏救赵”的感觉(即先求得正、余弦的关系再转化为正切).那么该问题可以直接求解吗？

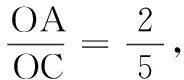
解法四：(解析法)在新的教材中，解三角形由原来独立的一章并入到“向量”这一章节之中.那么本题能否从向量的角度求解呢？通过建立直角坐标系，表示出各点的信息再利用垂直条件求解.

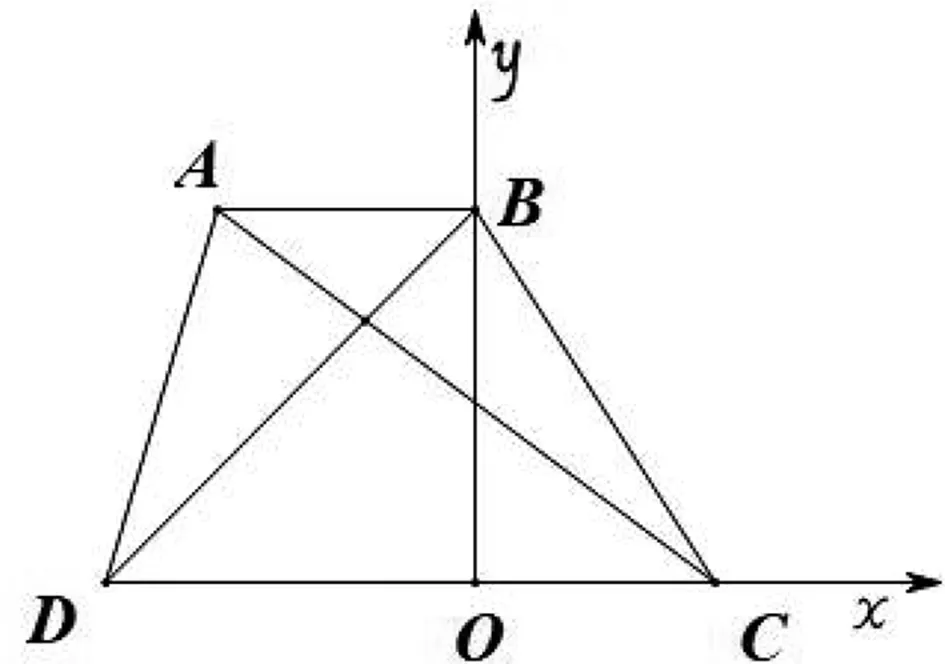
图3

解法五：(一般的向量法)在上述解法中，通过建系，本质上选择了一组单位正交基底.那么能否选择一般的基底利用向量进行求解呢？

三、背景探究及模型推广

根据上面的解答过程可知，该“梯形”的基本量之间满足某种固定的联系.接下来，笔者尝试推测其相关关系.现研究如下的一般性问题：

如图1，在梯形ABCD中，AB//CD，AB=m，CD=n，BC=t，∠BCD=θ，且AC⊥BD.试探究m,n,t,θ(m

接下来笔者还讨论了四边形四条边的关系.

设AD=s，则有m2+n2=s2+t2.该结论并不受“梯形”的限制，当“凸四边形”对角线垂直时，该四边形的四边即满足上述关系.现简要证明如下：

图4

如图4，在凸四边形ABCD中，AB=m，CD=n，BC=t，AD=s，则有AC⊥BD等价于m2+n2=s2+t2.

证明：(充分性)若AC⊥BD，分别考虑△AOB，△BOC，△COD，△AOD.应用勾股定理得m2=OA2+OB2；t2=OB2+OC2；n2=OC2+OD2；s2=OD2+OA2.上式相加即可得结论成立.

(必要性)设∠AOB=θ，在上述四个三角形中分别使用余弦定理得m2=OA2+OB2-2OA·OBcosθ；t2=OB2+OC2+2OB·OCcosθ；n2=OC2+OD2-2OC·ODcosθ；s2=OD2+OA2+2OD·OAcosθ.由m2+n2=s2+t2可得(OA·OB+OC·OD+OB·OC+OD·OA)cosθ=0.即可得cosθ=0，从而AC⊥BD.命题成立.

基于上面的分析，笔者设计了如下几个变式供读者练习.

变式1 在梯形ABCD中，AB//CD，AB=2，CD=5，若AC⊥BD，则BC的取值范围是.

变式2 在梯形ABCD中(CD>AB)，AB//CD，AB=2，BC=4，若AC⊥BD，则CD的取值范围是.

变式3 在梯形ABCD中(CD>AB)，AB//CD，CD=5，BC=4，若AC⊥BD，则AB的取值范围是.

答案：(2,5)；(4,8)；(0,4).