一道函数对称性与周期性的高考题探究

广东省深圳中学 (518001) 黄文辉

1.考题呈现

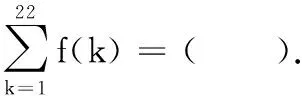
A.-21 B.-22 C.-23 D.-24

这是2022年全国乙卷理科选择压轴题，主要考查抽象函数对称性及周期性的相关性质，实际上，高中阶段对函数对称性考查的重点在轴对称和中心对称，即函数的奇偶性.而关于周期性的认识主要是通过三角函数，同时三角函数也具有良好的对称性.本文通过奇偶性推广到一般的函数关于x=a轴对称与关于点(a,m)中心对称的代数形式，同时给出对称性与周期性的一个关系及其应用.

2.性质归纳

此性质的证明与性质2类似，有兴趣的读者自行证明.

性质5 定义在D上的连续可导函数f(x)，若函数f(x)关于x=a轴对称的充要条件是其导函数f′(x)关于(a,0)中心对称.

证明：(必要性)由函数f(x)关于x=a轴对称则f(x)=f(2a-x)，两边求导数可得f′(x)=-f′(2a-x)，即f′(x)+f′(2a-x)=0，所以f′(x)关于(a,0)中心对称.

性质6 定义在D上的连续可导函数f(x)，若函数f(x)关于(a,c)中心对称的充要条件是其导函数f′(x)关于x=a轴对称.

此性质的证明与命题5类似，此略.

性质7 函数f(x)的定义域为D，条件：①函数f(x)的图象关于x=a轴对称；②函数f(x)的图象关于x=b轴对称；③函数f(x)的周期T=2|a-b|(其中a≠b).其中任意两个为条件可以推出另外一个成立.

证明：(先证①②⟹③)由函数f(x)的图象关于x=a轴对称，所以f(x)=f(2a-x)，由函数f(x)的图象关于x=b轴对称，所以f(2a-x)=f(2b-2a+x)，联立两式可得f(x)=f(2b-2a+x)，故函数的周期T=2|a-b|.

(再证①③⟹②)由函数f(x)的周期T=2|a-b|，可得f(2b-x)=f(2b-x+2a-2b)，即f(2b-x)=f(2a-x)，由函数f(x)的图象关于x=a轴对称，所以f(x)=f(2a-x)，即f(2b-x)=f(x)，所以函数f(x)的图象关于x=b轴对称.

同理可证②③⟹①.

性质8 函数f(x)的定义域为D，条件：①函数f(x)的图象关于(a,c)中心对称；②函数f(x)的图象关于(b,c)中心对称；③函数f(x)的周期T=2|a-b|(其中a≠b).其中任意两个为条件可以推出另外一个成立.

此性质的证明与性质7类似，此略.

性质9 函数f(x)的定义域为D，函数f(x)的图象关于x=a轴对称，且函数f(x)的图象关于(b,c)中心对称(其中a≠b)，则函数f(x)的周期T=4|a-b|.

证明：由函数f(x)的图象关于x=a轴对称得f(x)=f(2a-x)，由函数f(x)的图象关于(b,c)中心对称可得f(2a-x)+f(2b-2a+x)=c，联立两式可得f(x)+f(2b-2a+x)=c，根据x的任意性可得f(2b-2a+x)+f(4b-4a+x)=c，两式相减可得f(x)=f(4b-4a+x)，所以函数f(x)的周期T=4|a-b|.

3.性质应用

C.f(-1)=f(4) D.g(-1)=g(2)

4.考题析解