一道解几试题的命制、求解、测评及教学启示*

福建省福清第三中学 (350315) 何 灯福州教育研究院 (350001) 余小萍

2022年4月，笔者有幸参与福州市高二期中考试的命题工作.试卷的压轴题是一道解析几何问题，由于经历了该题的命制、修正、定稿、检测、阅卷、评价整个过程，笔者对此颇有感触，遂整理成文，与同仁交流.

1、试题命制

命题双向细目表中设定最后一道解答题考查椭圆及其性质，考查直线与椭圆的位置关系，体现基础性、综合性与创新性，预估难度0.3.

题型设定：参照细目表要求，笔者设定试题第二小题考查直线过定点问题(由于定值较易通过特殊情形猜测得到，故此处规避了定值问题的考查).

素材选取：由于命题时间有限，故笔者尝试从现有试题入手进行适当的改编.在查询资料过程中，笔者关注到试题(2022届皖豫联盟第二次联考理科数学第21题)：

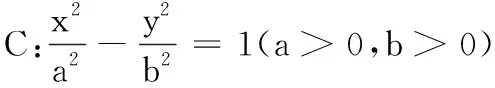
(1)求双曲线C的方程；

(2)设斜率分别为k1,k2的两条直线l1,l2均经过点Q(2,1)，且直线l1,l2与双曲线C分别交于A,B两点(A,B异于点Q)，若k1+k2=1，试判断直线AB是否经过定点，若存在定点，求出该定点坐标；若不存在，说明理由.

注意到问题(2)结论具有一般性，基于类比思想，笔者尝试将上述问题迁移到椭圆中.

(1)求椭圆C的标准方程；

(2)设斜率分别为k1，k2的两条直线l1，l2均经过点A，且直线l1，l2与C分别交于E，G两点(E，G异于点A)，若k1+k2=1，试判断直线EG是否经过定点？若是，求出定点坐标，若不是，请说明理由.

存在问题：本题问题(1)考查椭圆标准方程的求解，题型较常规；问题(2)中点A为象限内的点，导致后面计算k1+k2得到的形式较为复杂，给学生运算求解问题增加难度.基于试题重在考查学生思维，而非依赖运算增加学生求解难度，立足本市学情，平衡整卷考查的知识、能力、思想、素养的分布，命题组商讨后，建议对试题进行适当调整.

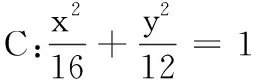
(1)证明：|PF|≥2；

(2)过点A分别作斜率为k1，k2的直线l1，l2，l1与C的另一个交点为E，l2与C的另一个交点为G.若k1+k2=1，试判断直线EG是否经过定点？若是，求出定点坐标，若不是，请说明理由.

考查意图：本小题主要考查椭圆的图象和性质、直线和椭圆的位置关系等基础知识；考查推理论证能力、运算求解能力；考查函数与方程思想、数形结合思想、化归与转化思想；考查直观想象、逻辑推理、数学运算等核心素养，体现基础性、综合性与创新性．

2、试题求解

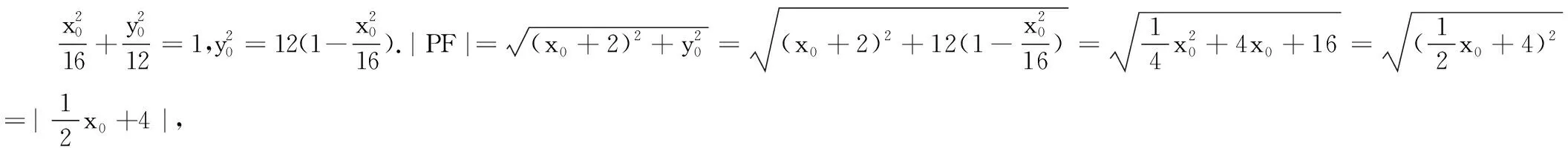
解法二：当P点运动到A点位置时，可得|PF|=a-c=2；当P点运动到C的右顶点时，可得|PF|=a+c>2；当P点不在x轴上时，设F′为C的右焦点，在△PFF′中，可得|PF′|-|PF|<|FF′|，结合|PF′|+|PF|=2a=8，可得(8-|PF|)-|PF|<4，|PF|>2.综上得|PF|≥2.

问题(2)解法一：(由于求解方法较多，此处仅给出阅卷过程中出现较多的两种解法)设E(x1,y1)，G(x2,y2).

①当直线EG的斜率不存在时，点E,G关于x轴对称，k1,k2互为相反数，k1+k2=0≠1，与条件矛盾.

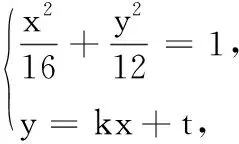
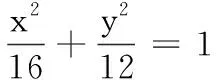
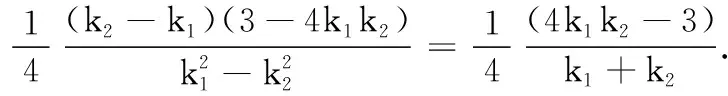
化简整理得y=

3、试题测评

(1)得分情况

试题满分值12分，全市平均得分1.10分，问题(1)满分值4分，全市平均得分0.83分，问题(2)满分值8分，全市平均得分0.27分.

(2)典型错误及失分原因分析

问题(1)常见的错误有三个：

其二、认为当PF⊥x轴时(此时|PF|长为通径的一半)|PF|取得最小值.失分原因是学生思维定势，认为凡是垂直的时候，取值都是最短的.

其三、没有经过严格的逻辑推理论证，直接利用了二级结论，得到|PF|≥a-c=2，导致大部分学生只能得到1分.失分原因是二级结论在解答题中的使用，需要先证明，教师在教学中必须让学生牢记.

问题(2)常见的错误也有三个：

其一、大部分学生采用假设直线l1，l2的方程(其中一部分学生假设直线l1方程错误，如写为y=k1(x-4)，或y=k1(x+2)等等)，导致求解出的E,G坐标形式较为复杂，无法继续做下去，只能拿到较低分数.失分原因是应根据题设条件合理假设直线方程，展开问题求解，这样才能能够帮助我们揭示问题本质，减少运算量.

其二、假设直线EG方程为y=kx+t，没有考虑到斜率k不存在的情形，假设直线EG方程为x=my+t，没有考虑到m=0的情形.失分原因主要是平时解题过程中，没有关注这些特殊情况.

其三、很大部分学生，假设直线EG方程之后，在处理完四步骤：联(联立方程)、消(消元)、判(判别式)、韦(韦达定理)后，就不再继续做下去，或者运算能力没跟上，导致计算错误.失分原因主要是圆锥曲线解答题较难，很大部分学生存在严重的畏难情绪，仅希望得到基础分.

4、教学启示

(1)二级结论能够帮助我们快速的求解问题，课堂上，教师可以介绍一些常见的二级结论，在精不在多，更要进行严格的论证，让学生知其然，更知其所以然.另外，应强调：二级结论在解答题中，要经过严格证明了，才能使用.

(2)解析几何的学科特点就是“算”，它的难也难在运算上，而能力也恰恰体现在如何简化运算上.教学过程中，提高运算能力不能仅从代数角度入手，单纯提升学生代数算式的恒等变换能力，还要努力提高学生的几何图形分析能力，这样才能从根本上提升学生的解几问题的求解能力.

(3)试题始终在变，但万变不离其宗.教学过程中，一味的追求题量，追求多种解法，并不可取.在教学过程中，更应该关注解法的生成过程，让学生掌握通性通法的同时，也要给解法的每个步骤寻求一个合情合理的解释(为什么是这样解的？其中蕴含了哪些东西？)，让解法生成的更自然一些.

(4)对试题进行深度挖掘，能够帮助学生把握试题本质，达到会一道而通一片的效果.本题还可继续引导学生探究k1+k2=t(t∈R)时，直线EG过定点的坐标；k1k2=t(t∈R)时，直线EG过定点的坐标；研究更一般的椭圆或双曲线，定点坐标又将如何？条件与结论进行适当的调换，是否仍然能够成立？这样的结论能否迁移到抛物线之中？等等.通过这些教学情境的创设，能够帮助学生掌握知识、熟练方法、体会思想，在潜移默化中提升学生能力，发展理性思维，培养起他们的数学核心素养.