EPnL: 一种高效且精确的PnL 问题求解算法

王平 何卫隆 张爱华 姚鹏鹏 徐贵力

基于直线特征的摄像机绝对位姿估计问题在计算机视觉领域称之为Perspective-n-line (PnL)问题,目的是通过目标物体上的n条已知直线和其所对应的图像投影来计算相机和目标之间的相对位置和姿态关系.PnL 问题是视觉导航[1−2]、机器人视觉定位[3]、传感器标定[4]、现实增强[5]等领域中的关键核心问题之一.到目前为止,现有解决PnL 问题的方法可以粗略分为迭代法和非迭代法:

迭代法将PnL 求解问题转换为非线性最优化问题,并利用Gauss-Newton 法或Levenberg-Marquardt法[6]迭代求解这个非线性最优化问题.然而,迭代法对初值的选取比较敏感,初值选择不合理将导致迭代法收敛速度较慢,影响算法的实时性.除此之外,当使用特征直线较少的时候,迭代法容易陷入局部最优,影响PnL 问题求解的精度和可靠性.

在非迭代法中,最直接的当属直接线性变换(Direct linear transformation,DLT)方法[7].DLT方法简单高效,但抗噪能力不强,在空间参考直线较少的情况下求解精度不高.Přibyl等[8]通过将直线在欧氏空间的坐标表示转换到普吕克(Plücker)空间,提出了解决PnL 问题的DLT-Plücker-lines方法.相比于DLT 算法,DLT-Plücker-lines 算法具有更好的抗噪能力和求解精度,但其求解时需要至少9 条以上的空间参考直线.随后,Xu等[9]通过借鉴Perspective-n-point (PnP)算法原理,提出了一系列线性求解PnL 的方法,但这些方法仍需要6条以上的空间参考直线才可以求解.最近,Přibyl等[10]基于DLT 的方法,提出了DLT-combined-lines的方法,该方法将线性求解PnL 问题的直线数目缩减到了5 条.DLT-combined-lines 方法求解效率高,在直线数目较多的时候,具有很高的求解精度,但是在直线数目较少的情况下,求解精度较差.

虽然直接线性求解PnL 的方法具有简单、效率高的特点.但是由于其抗噪能力差、不适合参考直线较少的情况(尤其不适合参考直线少于6 条以下的情况).为了克服这些问题,Ansar等[11]将PnL 问题转换为非迭代优化 开发了一种通用的PnL 求解算法,该算法能够处理从4到n条所有的空间参考直线.然而,文献[11]算法在空间直线较少的时候求解精度不高,这主要是因为其最优化求解过程中采用了线性化的策略.为了提高PnL 算法的求解精度,Mirzaei等[12]提出了一种直接求解PnL 问题全局最优解的方法,通过Cayley 参数的方式参数化旋转矩阵,然后通过矩阵分解和合成的方式,将PnL 位姿测量问题转换为最优化问题,最后通过矩阵合成技术求解这个最优化问题,得到PnL 问题的解.然而,文献[12]的方法由于使用了Cayley 参数表示旋转矩阵,求解过程中容易出现矩阵奇异值,导致求解稳定性不好.为了克服这个问题,Zhang等[13]提出了RPnL 方法求解PnL 问题,该方法将空间参考直线三条线为一组,然后利用Perspective-3-line (P3L)约束构建多项式方程组来求解PnL 问题.然而,RPnL 是一种次优化的方法,其求解精度还有提升的空间.2017 年,Xu等[9]改进了RPnL 方法,提出了ASPnL 算法.到目前为止,ASPnL 是求解精度最高,最稳定的PnL 算法之一.然而,ASPnL随着直线数量的增加,其求解消耗时间将快速增长,不利于其应用在实时性较高的任务中.2019 年,Wang等[14]对RPnL 算法增加优化步骤,并且使用矩阵化的方式替代RPnL 算法中的循环步骤,提出了改进的SRPnL算法,该算法求解精度和可靠性类似于ASPnL 算法,但效率远高于ASPnL 算法.

从以上文献分析可以看出,线性求解PnL 问题的方法效率高,但精度低,通常无法适用于直线数量小于6 的情况.非线性求解PnL 的方法适应性较广(适应4～n条直线求解),求解精度高,但是求解过程复杂,效率低下.针对以上问题,本文提出了一种同时兼具求解效率和求解精度的方法(命名为EPnL 方法).本文的主要贡献有:

1) 提出了分类表示旋转的方法: 最近的PnL问题求解中多使用Cayley 参数[13−15]和四元数表示[16]旋转,然而利用Cayley 参数求解PnL 问题容易出现奇异值,导致求解结果不稳定.利用四元数表示旋转则存在解的符号模糊问题,会增加PnL 问题求解的复杂性,降低求解效率.针对以上缺点,本文基于四元数参数中变量不同时为零的特性,提出了分类表示旋转的方法,在保证不损失旋转正交约束信息的前提下,避免了Cayley 参数求解奇异性和四元数参数对解符号模糊的问题,提升了求解PnL 问题的可靠性和效率.

2)将PnL 问题转换为了二次曲面(曲线)方程组求交点的问题: 本文首先通过矩阵变化的方式统一求解参数的度量空间,消除求解参数度量空间不同可能引起的算法不稳定因素.然后,不同于现有文献[12−14]直接最优化求解PnL 问题的方式,本文基于1)中分类表示旋转的方法,将PnL 问题转换为二次曲面(或曲线)求交点的问题来解决,有效地降低了PnL 问题求解的复杂度.

3)利用方程组低次项参数化高次项的方式将复杂二次曲面(曲线)方程组求交点问题转换为单变量多项式求解问题: 针对迭代法求解耗时且容易陷入局部最优,而Gröbner 基方法[17]求解复杂,无法保障可靠性的问题.本文利用二次曲面方程组自身的结构信息,将方程组划分为高次项和低次项部分,并通过引入恒等式的方式将高次项用低次项表示,最终将复杂的多变量二次曲面求解问题转换为简单的单变量多项式(最高为8 次)求解问题来解决.同时,本文利用少量Gauss-Newton 法对结果进行精定位,以进一步提升最终的求解精度.

4)本文提出的算法实现了求解精度和效率的统一.实验部分选择和主流及最新的PnL 算法对比,结果表明,EPnL 适用于3～n条直线的位姿求解,具有通用性.在所有对比算法中,EPnL 算法求解精度最高,效率仅次于线性DLT 的方法(排名第2).本文中所有方法的源代码已公布1https://sites.google.com/view/ping-wang-homepage,读者可以下载验证.

1 PnL 问题的描述

基于相机的透视成像模型,PnL 问题如图1 表示,其中Li=(vi,Pi) 表示3D 空间中的某条已知直线,vi∈R3为Li的方向向量,Pi∈R3为Li上的任意一点.li=(si,pi) 为Li在图像平面上的投影直线,si和pi分别为li的两个端点.直线Li,li和相机光心O共同形成平面πi,且ni为平面πi的法向量.当相机内参数标定的情况下,ni很容易由光心和投影直线两个端点所形成向量的外积得到,即:

图1 PnL 问题Fig.1 PnL problem

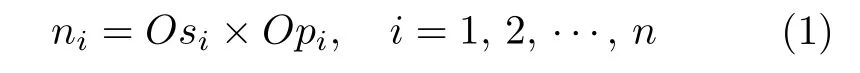
由于直线Li在平面πi内,因此其和平面法向量ni满足垂直的关系,即:

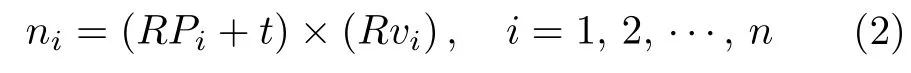
式中,R∈SO(3) 为3 × 3 矩阵,表示相机坐标系和空间直线所在坐标系(世界坐标系)之间的旋转关系;t∈R3为3 × 1 向量,表示相机坐标系和世界坐标系之间的平移关系.式(2)可进一步展开为:

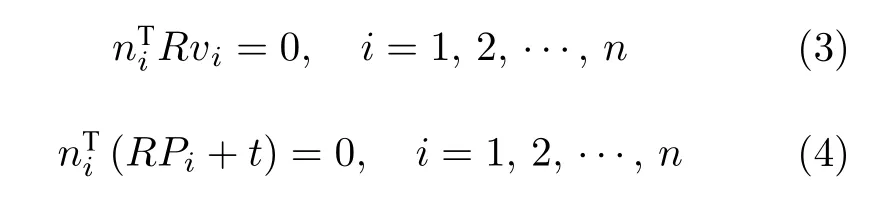
PnL 问题的目标就是在空中直线Li和其投影li已知的情况下,利用式(3)和式(4)计算R和t.

2 约束方程组的构建

PnL 问题中旋转矩阵R和平移向量t的度量空间是不同的,这在优化求解过程中容易导致系数矩阵中元素数值的差异过大,最终影响PnL 问题的求解精度.由式(4)可以看出,平移t和旋转R之间呈现线性关系.因此,本文采用矩阵变化的方式,基于空间所有的直线信息,利用旋转R参数化平移t,进而统一PnL 问题中待求解参数变量的度量空间,以最终提升求解PnL 问题的可靠性和精度.式(3)进一步可以表示为:

综合式(4)和式(5),将其写为矩阵形式:

式(6)对空间中的每一条参考直线都满足,因此有:

基于式(7),t可以表示为:

式中,B+=(BTB)−1BT为B的广义逆.由式(8)中可以看出,B+,A和D中包含空间所有直线提供的已知信息,W由旋转R构成.因此基于式(8),平移向量t可以表示为旋转R的参数化形式.进一步将式(8)代入式(6)得到:

式(9) 依旧对空间的n条直线都满足,将式(9)变为矩阵形式得到:

由式(10) 可以看出,A、D、B+、Ai、Di和Bi(i=1,2,···,n) 均可以由已知的ni、vi和Pi提前计算得到.式(10)中的未知数仅由C和W提供,而C和W由旋转未知变量R构成.此时,如果能够利用式(10)求解得到旋转变量R,则平移向量t可以由式(8)给出,即PnL 问题得到求解.R和t的具体求解方法,本文将在第4 节重点展开研究.

3 基于四元数的旋转分类表示法

由式(10)可以看出,R的表示形式直接影响着式(10)的复杂程度和求解系数矩阵的奇异性,进而间接影响优化求解PnL 算法的精度、可靠性和效率.R的表示形式通常包括: 欧拉角表示形式、旋转矩阵表示形式、Cayley 参数表示形式、四元数表示形式、对偶四元数表示形式、角轴参数表示形式.其中四元数表示含有正交约束信息,且其形式不具有奇异性,因此利用四元数解决PnL 问题具有精度和可靠性高的特点.四元数表示R的形式如下:

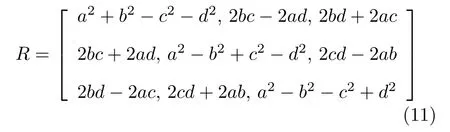
式中,a、b、c和d为变量且满足约束条件a2+b2+c2+d2=1.由式(11)可以看出,利用四元数求解旋转时,[a,b,c,d]T和[−a,−b,−c,−d]T表示相同的旋转,这说明四元数对变量的正、负号无法分辨,这无疑将扩大求解PnL 问题时解的搜索空间,增加求解问题时的复杂性,降低求解问题的效率.

由四元数约束a2+b2+c2+d2=1 可以看出,四元数在表示旋转时,参数a、b、c和d是不同时为0 的.基于这个特点,根据a、b、c和d的取值,本文提出基于四元数的旋转R分类表示方法:

1)形式1.当a、b、c和d都不为0,任选一个变量(如a),在R右端提取出 1 /a2且令s1=b/a,s2=c/d和s3=d/a,则R变为:

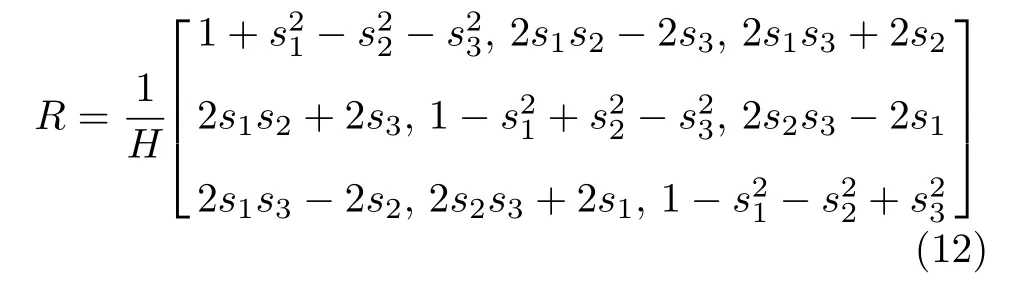
2)形式2.当a、b、c和d中有一个变量为0,例如a=0,b0,c0和0.则任选一个不为0 的变量,例如用b来化简R,则可得:

式中,s2=c/b,s3=d/b,且H=

3)形式3.当a、b、c和d中有两个变量为0,例如a=0 ,b=0,c0和d0 .任选c和d中的一个变量,如c化简R得到:

式中,s3=d/c,并且有H=1+

4)形式4.当a、b、c和d中仅有一个变量不为0,例如a=0 ,b=0 ,c=0和0 ,则R直接表示为:

通过以上分类表示R的方式,在保证不损失四元数正交约束信息的前提下,避免了四元数对解符号模糊的问题,有效降低了求解PnL 问题时未知变量的个数和解空间的维度,在理论层面保障了求解PnL 问题的可靠性和效率.

4 旋转矩阵和平移向量的求解

本节将旋转R的4种形式分别代入式(10)进行求解.

1)对于形式1.将式(12)代入式(10),进一步展开,合并同类项得到:

式中,E1为已知的2n×10 矩阵,可以由A、D、B+、Ai、Di和Bi(i=1,2,···,n) 计算得到.β1=为式(12)的向量形式.对于式(16),可以采用Newton 法和Gauss-Newton法[6]等迭代法求解.然而,迭代法对初值的选择敏感,初值选取不好的时候容易导致迭代陷入局部最优.此外,迭代法求解过程中需要耗费较多的时间.为克服此问题,最近的研究[15−16]中将类似式(16)的等式转换为无约束最优化问题,通过Gröbner 基方法[17]构建矩阵消去模板来求解.然而,Gröbner 基方法求解式(16)时需要对其两端取平方,这将引入较多高次未知数,导致Gröbner 基方法构建的矩阵消去模板过于复杂,无法保证求解的可靠性.除此之外,矩阵消去模板越复杂,算法的计算效率也越低,并且复杂的矩阵消去模版更不利于算法的工程实现.

由式(16)可以看出,β1中含有3 个未知数,且所含未知数的最高次数为2.因此式(16)中每一行都代表着一个二次曲面,可以将求解式(16)看作为求解一组二次曲面交点的问题.观察式(16)结构可以发现,将变量s1看作为常量,s2和s3为变量,则E1可以被划分为两部分:

式中,E1(i),i=1,2,···,10 表示E1的i列,G1(s)中的每一个元素都是变量s1的多项式.式(17)进一步可变为:

通过以上划分方式,可以将式(16)中的高次项部分通过低次项部分来表示.利用式(16)中高次项和低次项之间的关系引入以下恒等式:

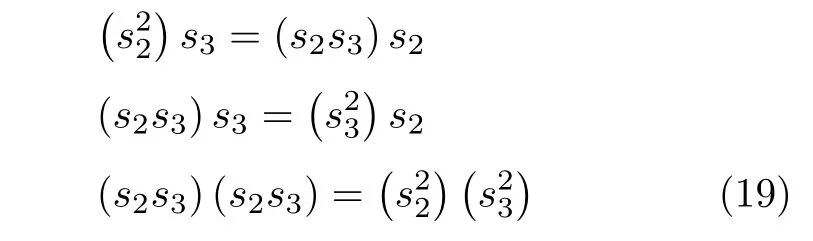
通过式(19)的恒等式,可以建立起式(16)中高次项之间的联系.将式(18)再次代入式(19),展开可得:

将式(20)、式(21)和式(22)展开为:

式中,Ui,i=0,1,···,4 为系数.采用特征值分解的方法,式(34)很容易求解,一旦得到s3,将其代入式(14)和式(8)可得完整的R和t.

4)对于形式4.式(15)中R的值已知,将其直接代入式(8)可得t.

由以上求解可以看出,式(25) 有8 个解,式(31)有1 个解,式(34)有4 个解,求解形式4 有1 个解.因此,求解以上形式最多得到14 个解,其分别对应着14 组R和t. 将每组R和t分别代入式(10),选择其误差最小的那组R和t作为最终结果输出.表1 列出了文献中各非线性求解PnL 问题算法解的个数.从表1 可以看出,本文提出方法解的个数最少,有利于提升算法的求解效率和求解可靠性.

表1 解的个数对比Table 1 Comparison of the number of solutions

5 实验结果

本节通过实验验证本文提出的EPnL 算法性能,并与现有主流算法进行对比.对比算法主要分为线性算法和非线性算法两类,其中线性算法有DLT-Lines[7]和LPnL-Bar-LS[9]算法;非线性算法有 Lift[11]、AlgLS[12]、RPnL[13]、ASPnL[9]和SRPnL[14]算法.

实验中的源代码可以从作者个人网站https://sites.google.com/view/ping-wang-homepage 下载.

5.1 仿真实验

合成分辨率为640 × 480 像素,焦距为800 像素的虚拟相机.在相机坐标系下产生空间3D 直线:在普通情况下,空间直线随机分布在 [ −2,2] ×[−2,2] × [ 4,8] 的范围内;在共面情况下,空间3D直线随机分布在 [ −2,2] × [ −2,2] × [ 0,0] 内.利用随机产生的旋转矩阵Rtrue和平移向量ttrue将相机坐标系下的3D 直线转换到世界坐标系.利用合成的虚拟相机,将相机坐标系下的3D 直线投影到图像平面上,并根据仿真实验参数的不同,给投影直线增加不同等级的噪声δ.为了误差评估的一致性,本文使用文献[9−15]的误差定义形式:

式中,rk,true和rk分别表示Rtrue和R的第k列.

1)直线数量对算法精度的影响.首先设置仿真噪声δ=5,通过改变输入参考直线数量4～20 来验证各PnL 算法的求解精度,结果如图2 所示 (部分算法共面情况下幅度超出显示范围).由图2 可以看出,线性的DLT-Lines和LPnL-Bar-LS 方法在普通和共面情况下求解精度都不高,且在直线数量少于6 时无法正常求解.Lift 是一种非迭代的方法,但由于其求解过程中使用了线性化的策略,因此在普通情况(共面情况下无法求解)下求解精度不高.AlgLS 的中值求解精度很高,但是其平均求解精度反而较低,原因是AlgLS 方法采用了Cayley 参数表示旋转矩阵,导致计算的时候容易出现奇异性,影响算法的整体计算精度.RPnL 是一种次优化方法,在普通情况下求解精度较高,在共面情况下求解精度较差.ASPnL 算法作为RPnL 算法的改进版本,在普通情况下能取得很高的求解精度,但在共面情况下平均求解精度较低.SRPnL 方法作为RPnL 方法的另一种改进版本,在普通和共面情况下都能取得较高的求解精度.相比之下,本文的EPnL 采用了全局优化的方式求解,并且在求解过程中分类考虑了旋转的情况,避免了求解过程中的奇异性,因此在普通和共面情况下都能保证最好的求解精度.

2)噪声对算法精度的影响.固定空间直线数量为10,改变噪声等级δ为1～15 来验证各PnL 算法的求解精度,结果如图3 所示.可以看出,随着噪声等级的增加,各算法的求解精度都在下降,且噪声等级和求解误差的增加近似符合线性关系.由图2～3 可以看出,本文PnL 算法在普通情况和共面情况下都能取得最好的求解精度.

图2 当直线数目变化时旋转和平移误差的均值和中值Fig.2 The mean and median of rotation and translation errors when the number of lines varies

图3 当噪声等级变化时旋转和平移误差的均值和中值Fig.3 The mean and median of rotation and translation errors when the noise level varies

3)对比P3L 算法.本文算法虽然不是为求解P3L 问题设计的,但是可以处理P3L 问题.图4 为本文算法和现有最新P3L 算法[13,19]的对比结果.由图4 可以看出,本文EPnL 算法不仅能够处理P3L问题,而且还具有较高的求解精度.

图4 最小情况下(n =3)旋转和平移误差的均值和中值Fig.4 The mean and median of rotation and translation errors in the minimal case (n =3)

4)对比运行效率.图5 为各PnL 算法的运行效率曲线图.测试直线的数量从4 到2 000 条,足够覆盖大多数的实际应用场合.测试时每种算法分别执行500 次,并统计其平均运行时间.由图5 可以看出,RPnL和ASPnL 算法初期运行效率高于AlgLS 的方法,但是随着直线数目增加,其消耗的时间呈指数状增加,效率反倒低于AlgLS 方法.DLT-Lines和LPnL-Bar-LS 由于是线性求解的方法,因此求解效率很高.SRPnL 方法相比于RPnL和ASPnL 方法具有较高的求解效率,但是随着直线数量的增加,其时间消耗也急剧增加.相比之下,本文提出的EPnL 方法具有很高的求解效率,当直线数量超过300 条的时候,求解效率甚至高于线性的DLT-Lines 的方法,仅次于LPnL-Bar-LS 方法.综合考虑EPnL 算法的求解精度、求解效率和求解通用性,其在所有对比方法中综合性能更优,非常适合于实际项目应用.

图5 对比算法的计算效率Fig.5 The computational efficiency of compared the methods

5.2 实际实验

牛津大学视觉测量组(Visual Geometry Group)建立了以其团队命名的(VGG)图像数据集2http://www.robots.ox.ac.uk/～vgg/.VGG数据集中包含7 组图像数据,每组数据中包含若干张采集的建筑物图像,图像中建筑物边缘直线的图像坐标及其对应世界坐标系中的位置、相机相对于世界坐标系之间的位姿关系都是已知的.因此可以使用VGG 数据集来测试各PnL 算法的求解精度.测试过程中各算法的求解误差定义如下:

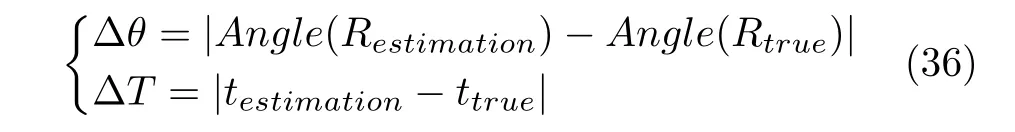
式中,Angle(·) 表示将旋转矩阵转换为欧拉角,Restimation和testimation表示各算法计算得到的旋转矩阵和平移向量,Rtrue和ttrue为数据集中真实的旋转矩阵和平移向量.分别利用各PnL 算法按式(36)计算每组图像数据的误差平均值,结果如表2 所示,每组中平均误差最小的值加粗表示.由表2 可以看出,本文提出的EPnL 算法在能够在4组测试集上同时获得最高的角度(旋转)和位置(平移)求解精度,并且能够在6 组测试集上获得最高的位置求解精度,其整体求解精度最好.为进一步验证EPnL 算法的求解精度,利用EPnL 算法求解的位姿信息将世界坐标系下建筑物的边缘投影到图像上,结果如图6 所示,其中青色直线为投影直线.由图6 可见,EPnL 算法能够准确的恢复位姿信息.

图6 VGG 数据集中的图片Fig.6 Images from the VGG dataset

表2 各算法在VGG 数据集上的旋转和平移误差均值Table 2 The mean of rotation and translation errors for each method on the VGG dataset

6 结束语

本文提出了一种精确且高效的PnL 问题求解算法(EPnL 算法).EPnL 首先通过矩阵变化的方式统一PnL 问题的度量空间,并将PnL 求解问题转换为求二次曲面(曲线)交点的问题.然后,针对现有Cayley 参数和四元数参数表示旋转时存在的问题,本文提出了基于四元数的旋转分类表示方法,该表示法在不损失旋转正交约束的前提下,能够有效提升求解PnL 问题的可靠性和效率.最后,针对现有迭代法和Gröbner 基法求解问题效率不高且无法保障可靠性的问题.本文提出利用二次项曲面方程组低次项参数化高次项的方法,将二次项曲面方程组求交点问题转换为单变量多项式求解问题解决.仿真和实际实验表明,相比于现有的PnL算法,本文算法在具有高求解精度的同时兼具高求解效率.