一种基于样本空间的类别不平衡数据采样方法

张永清 卢荣钊 乔少杰 韩楠 GUTIERREZ Louis Alberto 周激流

不平衡数据广泛存在于实际应用中,如何有效处理类别不平衡数据已成为目前机器学习领域一个重要的研究热点.许多生物信息学中的分类问题都面临不平衡数据的问题,如基因表达数据[1]、蛋白质−DNA 结合数据[2]、mRNA 中的甲基化位点[3]、拼接位置预测[4]、microRNAs 的预测[5]、蛋白质相互作用预测[6]等.此外,不平衡数据还广泛存在于医疗诊断[7−8]、诈骗交易[9]和网络入侵[10]等领域.在数据不平衡问题中,由于负样本(多数类)的数量远远大于正样本(少数类)的数量,使得少数类样本难以被分类器有效学习.此外,现有的机器学习算法一般假定类分布均衡或样本错分代价相同.然而,真实应用中通常少数类样本比多数类本更为重要,错分代价更高.所以对不平衡数据的学习一般无法取得令人满意的结果.

现有方法一般通过数据预处理的方式来重构数据集,以减少学习过程中样本偏态分布的负面影响,重采样方法是其中经典的方法.重采样主要分为欠采样和过采样,使用欠采样算法可能会移除多数类中潜在的有用信息,导致分类性能降低,并且可能破坏样本原始分布.过采样算法会增加样本量,这会增加算法的时间成本,也容易导致过拟合[11].此外,新生成的样本不能保证与原数据有相同的分布.大多数方法将数据采样到所有类别样本数量一致为止,采样比例不仅取决于不平衡比例,还取决于数据的空间分布情况.因此重采样算法的一个难点在于如何确定采样比例,即 如何合理地根据数据本身的特点确定具有最佳分类性能的采样比例.

基于上述问题,亟需提出一种先进的数据采样方法来处理正负样本比例不平衡问题.本文研究基于以下几点考虑:

1)在不平衡数据中,负样本数量占据了绝大多数,虽然负样本与正样本属于不同的类别,但是在负样本中可能包括潜在的正样本,这是之前的研究没有考虑的.

2)如何根据数据整体的空间分布特点,自适应地确定采样比例.

3)基于混合采样方法能很好地避免单独使用欠采样和过采样带来的问题.

为解决上述问题,本文提出了一种新的基于样本空间的不平衡数据采样方法,伪负样本采样方法(Pseudo-negative sampling,PNS),本文主要贡献有:

1)提出了伪负样本概念.在大量的负样本中存在与正样本有类似分布的样本,因此与正样本具有很高的相似度,可以将它们定义为被错分了的正样本.基于这一观察,本文首次提出伪负样本概念,将与正样本相似度很高的负样本标记为伪负样本.

2)根据数据空间分布,提出一种度量正样本和负样本之间相似性的方法.算法工作原理为: 使用欧氏距离评价样本之间的相似性,首先计算正样本的空间中心,然后将正样本到空间中心的平均距离作为判断是否为伪负样本的阈值,最后分别计算每个负样本到空间中心的距离.如果其距离小于阈值,则将此负样本标记为伪负样本.将其添加到正样本集中.

3)通过正负样本之间的相似距离,自适应地确定不平衡数据采样的比例.

4)在多个UCI 数据、KEEL 数据和真实生物信息数据上进行了大量实验,全面验证了算法的准确率、敏感性、特异性、马修斯相关系数(Matthews correlation coefficient,MCC)、F-score和时间效率等性能评价指标.引入对比算法,从多角度验证所提出方法的性能优势.

本文结构如下: 第1 节综述主流的类不平衡数据解决方法;第2 节详细说明本文提出的PNS 采样算法;第3 节介绍本文使用的数据集和算法评价指标;第4 节对本文提出的采样方法的实验结果进行分析;第5 节对本文工作进行总结和展望.

1 相关工作

如何处理类别不平衡数据是分类中的一个关键问题,并受到广泛关注.现有方法可分为数据预处理[12−14]、代价敏感学习[15]和集成学习[16]三类.

数据预处理是最常用的方法,因为它独立于分类器,具有很好的适应性,主要包括过采样[17]和欠采样[18].过采样是通过创建新的少数类样本来消除偏态分布的危害,提高少数类的分类性能.最简单的方法是随机过采样(Random over-sampling,ROS),即随机复制少数类样本,缺点是少数类没有增加任何额外信息,只是简单复制,从而增加过拟合的风险,并且新的数据使训练分类器所需时间增加.在改进的过采样方法中,Chawla等[19]提出了Synthetic minority oversampling technique(SMOTE)算法,在少数类样本中随机插值邻居样本来生成新样本.但这种方法容易产生分布边缘化问题,新生成样本可能会模糊正样本和负样本的边界.虽然使数据集的平衡性得到了改善,但加大了分类算法进行分类的难度.Douzas等[20]将深度学习模型中的生成对抗网络用于少数类样本的合成,很好地平衡了数据集,并取得了较好结果.欠采样是通过移除多数类样本来消除偏态分布的危害,从而提高少数类的分类性能.最简单的方法是随机欠采样(Random under-sampling,RUS),即随机地去掉一些多数类样本,缺点是可能会丢失一些重要信息,对已有息利用不充分.Wilson[21]提出了一种最近邻规则欠抽样(Edited nearest neighbor,ENN)方法,基本思想是删除其最近的3 个近邻样本中具有2 个或者2 个以上类别不同的样本.但是大多数的多数类样本附近的样本都是多数类的,所以该方法所能删除的多数类样本十分有限.因此,Laurikkala[22]在ENN 的基础上提出了邻域清理规则欠采样方法 (Neighborhood cleaning,NCL),核心思想是找出每个样本的3 个最近邻样本,若该样本是多数类样本且其3 个最近邻中有2 个以上是少数类样本,则删除它;反之,当该样本是少数类,并且其3 个最近邻中有2 个以上是多数类样本,则去除近邻中的多数类样本.但是该方法中未能考虑到在少数类样本中存在的噪声样本,而且这种方法删除的多数类样本大多属于边界样本,对后续分类器的分类会产生很大的不良影响.

传统分类器在训练时,往往以最小化错误率为目标,这一目标是基于假设: 不同类之间的错误分类具有相同代价,因此不同类的错分可以被同等对待.然而在类别不平衡数据集中,多数类与少数类之间的错分代价往往是不同的,错分少数类具有更高的代价.基于这一前提,代价敏感方法通过引入代价矩阵为不同错分类型赋予不同代价,然后以最小化代价值为目标来构造分类器.Zhang等[23]将代价敏感学习应用于不平衡数据的多分类,通过一对一分解,将多分类问题转化成多个二分类子问题并使用代价敏感的反向传播神经网络进行独立学习,从而减小平均误分代价.Liu等[24]提出了一种新的代价敏感的支持向量机(Support vector machine,SVM)算法,该算法首先使用过滤式方法对特征进行挑选,同时对于代价敏感SVM 中的参数,使用元优化算法进行优化.实验表明,该方法在对乳腺癌数据的预测上取得了较好结果.

集成学习方法的主要思想是将多个不同的弱学习器组合在一起,形成一个强学习器.通过利用每个基学习器之间的差异,来改善模型的泛化性能.经典的方法有 Bagging和Boosting 等.Breiman[25]将自采样引入集成学习提出了Bagging 集成方法,他通过从原始数据集不断采样产生新的数据子集来训练每个新的分类器,由于数据子集的不同,保证了基分类器具有一定的多样性.Schapire[26]则提出了Boosting 集成方法,AdaBoost[27]是其中的代表性方法,它使用整个数据集来不断地训练分类器,在每一个分类器被训练出来后,后面的分类器将更多关注被错分的样本,从而提高少数类的精度.关注的方法是为样本设置权重,被前一个分类器正确分类的样本,权重将降低,反之将权重提高.

在相似性度量方面,欧氏距离作为一种简单有效的评价方式被广泛使用,其计算公式见下:

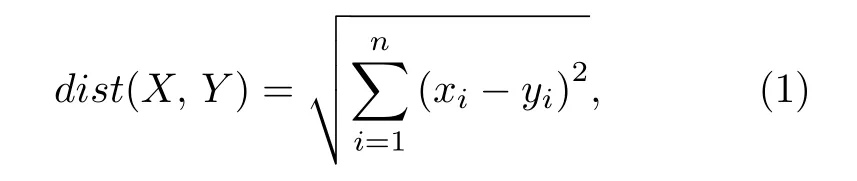
式中,X和Y表示2 个被考虑的样本,xi与yi表示样本X与Y的第i个特征,n表示特征数.Elmore等[28]提出了基于欧氏距离的主成分分析(Principal component analysis,PCA)方法.该方法使用基于欧氏距离得到的相似度矩阵,识别彼此接近的参数,为PCA 中相似性度量提供了更多选择.Park等[29]在对歌曲的相似性识别中,结合欧氏距离和汉明距离,提出了一种新的距离度量方法,称之为条件欧几里得距离.

通过上述工作分析可知,现有研究工作中存在的突出问题: 1)采样时,没有充分考虑数据的空间分布特点,特别是正样本集的分布,导致采样具有较大盲目性;2)需要人为指定采样比例,采样比例应该根据数据本身的特点确定,如何针对不同数据进行采样比例的适应性调整.

2 问题描述

2.1 伪负样本采样方法

算法中使用的主要符号及说明如表1 所示.

表1 符号及说明Table 1 Symbols and their explanations

在不平衡数据的负样本集中,可能存在潜在的正样本,本文称之为伪负样本.如果能有效地找出伪负样本,将其加入到正样本集中同时从负样本集中删除,便能得到一个数据分布更加合理的数据集.基于这个数据集训练的分类器可以更好地学习正样本集,从而提高正样本集的精确度.基于这一考虑,本文首次提出了伪负样本采样方法PNS.图1 描述了如何从多数类中找出伪负样本,图1 中空心圆代表多数类,空心五星代表少数类.首先需要找到少数类的空间中心,图1 中用实心五星表示,并得到所有少数类样本到空间中心的平均欧氏距离,然后分别计算所有多数类样本到空间中心的欧氏距离.若某个多数类样本到空间中心的距离越近,则认为该多数类样本与少数类样本相似性越高.如果某个多数类样本到空间中心的距离小于平均欧氏距离,则将此负样本认定为潜在的正样本即伪负样本.

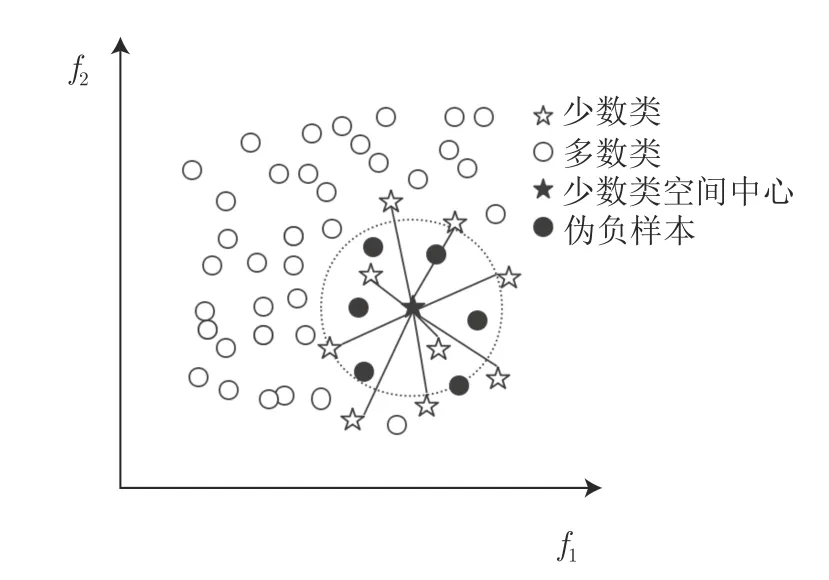
图1 伪负样本采样方法Fig.1 Pseudo-negative sampling method

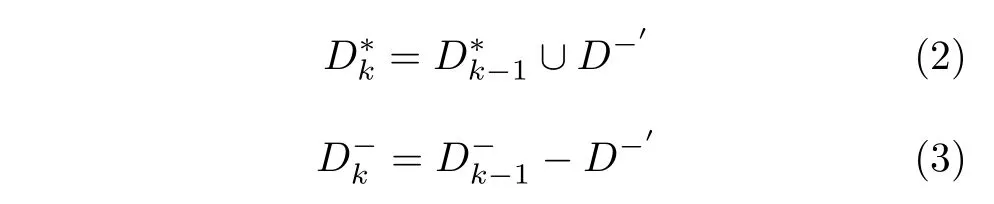
式中,k表示迭代次数,表示相似性大于阈值的负样本,表示上一次迭代后得到的伪负样本集.同理,表示上一次迭代后得到的负样本集.

迭代结束之后,将伪负样本集加入到正样本集当中,同时得到了平衡后的负样本集.具体计算过程将在第2.3 节给出.

2.2 基于欧氏距离的PNS 采样算法

PNS 算法是基于正样本集空间位置的,因此,首先需要找到正样本的空间中心点,空间中心点C是所有正样本的平均值,计算方法如下:

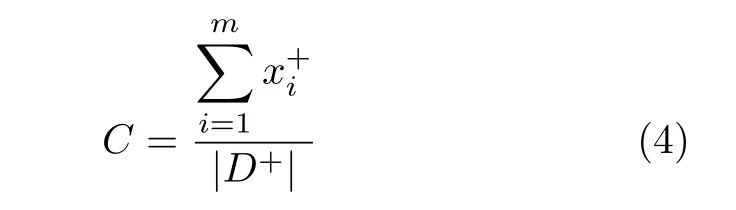
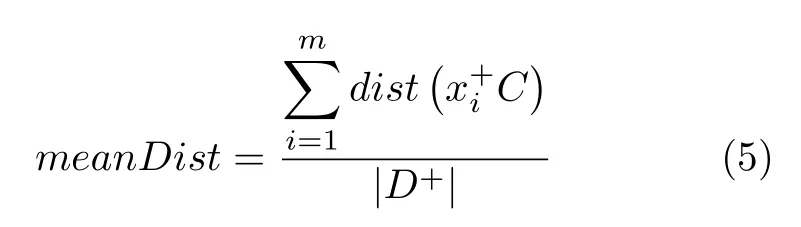
式中,dist() 表示正样本与空间中心C之间的欧氏距离.然后,计算每个负样本与正样本集的相似性,正样本集使用空间中心C代替,计算公式如下:

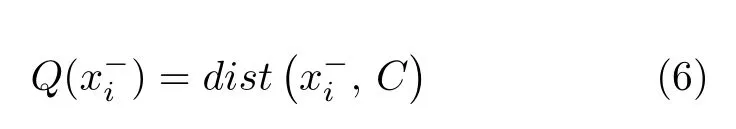
式中,i=1,2,3,···,n.dist() 表示负样本与空间中心C之间的欧氏距离,计算结果即为样本具有的相似性大小.然后将每个负样本的相似性与阈值meanDist进行比较,如果小于阈值,则认定该负样本为伪负样本,定义如下:

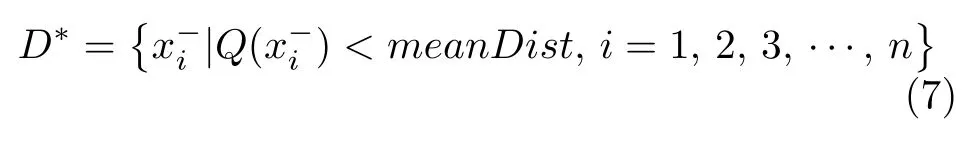
最终,将伪负样本集加入到正样本并从负样本集中删除,最终得到采样后的数据集:

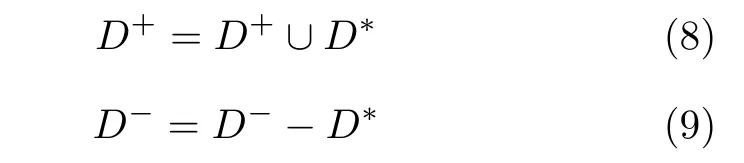
2.3 算法描述

基于上述讨论,给出本文算法的形式化描述,如算法1 所示.

算法基本步骤为: 第7～13 步将原始数据集分成正样本集和负样本集;第14～17 步计算正样本的空间中心C;第18～21 步计算少数类到空间中心的平均距离meanDist;第22～24 步计算每个多数类到平均中心的距离Distancei;第25～29 步根据多数类样本距离与平局距离判断某个多数类是否为伪负样本,如果是,则加入伪负样本;最后返回采样后的数据集.其中,dist(A,B) 表示计算A点到B点的欧氏距离.

算法复杂性分析: 本文提出的算法还具有良好的时间复杂度,由算法1 中可以看出,耗时操作主要集中在5 个循环操作上: 1)样本分离操作,时间复杂度为 O (k),其中k代表样本总数.2)计算正样本中心,时间复杂度为 O (m),m表示正样本数量.3) 计算正样本到中心的平均距离,时间复杂度为O(m).4)计算每个负样本到中心的距离,时间复杂度为 O (n),n表示负样本数量.5)将每个负样本到中心的距离与平均距离进行比较,时间复杂度为O(n). 综上,PNS 算法的总时间复杂度为O(k+2×m+2×n)n),由于在数据集中k等于m加上n,因此原式可化简为 O (3×k).由此看出,PNS 算法的时间复杂度较低,是一种高效的算法.

算法1.基于伪负样本的采样方法

2.4 对比采样方法

本文使用ROS、RUS、Adaptive synthetic sampling (ADASYN)和SMOTE 作为对比采样算法与PNS 进行比较.其中,RUS 属于欠采样,其余方法属于过采样.ROS与RUS 均是随机采样,前者通过随机复制少数类样本对数据进行采样,后者通过删除多数类样本进行采样.这两种方法具有实现简单,采样效果较好的特点.

SMOTE[19]方法基于少数类间的相似性合成新样本.对于少数类样本集Smin,首先计算得到每个样本xi∈Smin的K近邻.K近邻被定义为距xi最近的K个样本,距离计算通常是欧氏距离,整数K是人工指定的超参数.为了合成新样本,随机从K个近邻样本中选择一个求出两者的差,然后乘以介于[0,1]之间的特征向量差异随机数,最后加上原始特征xi.

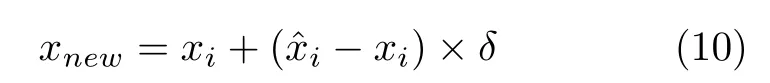
式中,xi∈Smin是正在被考虑的样本,是xi其中一个K近邻样本,且[0,1] 是一个随机数.因此,根据式(10)得到的合成实例是所考虑的xi与随机选取的K近邻的连线线段上的一个点.SMOTE 的提出避免了ROS 带来的过拟合问题,同时显著提高分类器性能.已经在各种领域得到了广泛认可.

He等[30]基于对SMOTE 的改进提出了ADASYN 采样.ADASYN 的主要思想是根据少数类的分布自适应合成新样本: 在合成新样本过程中,分类困难的少数类样本会生成更多样本,反之则会生成较少样本,以此将决策边界转移到难以学习的样本上.该方法与SMOTE 的不同点主要在于对少数类合成样本的控制.在SMOTE 中,对每个少数类都合成相同数量的样本,而在ADASYN 中,处于边界的少数类将合成更多样本.对边界的检测通过样本的K近邻得到,如果一个少数类的K近邻存在越多的多数类,那么这个少数类被认为离边界越近,会合成更多样本.

3 数据集及算法评价指标

3.1 数据集

为评价不同样本采样方法在不同数据集上的预测性能,并与其他常用采样方法进行比较,本文使用了7 个UCI 数据集[31]、4 个KEEL 数据集[32]和2个真实的生物信息学数据集.如表2 所示.

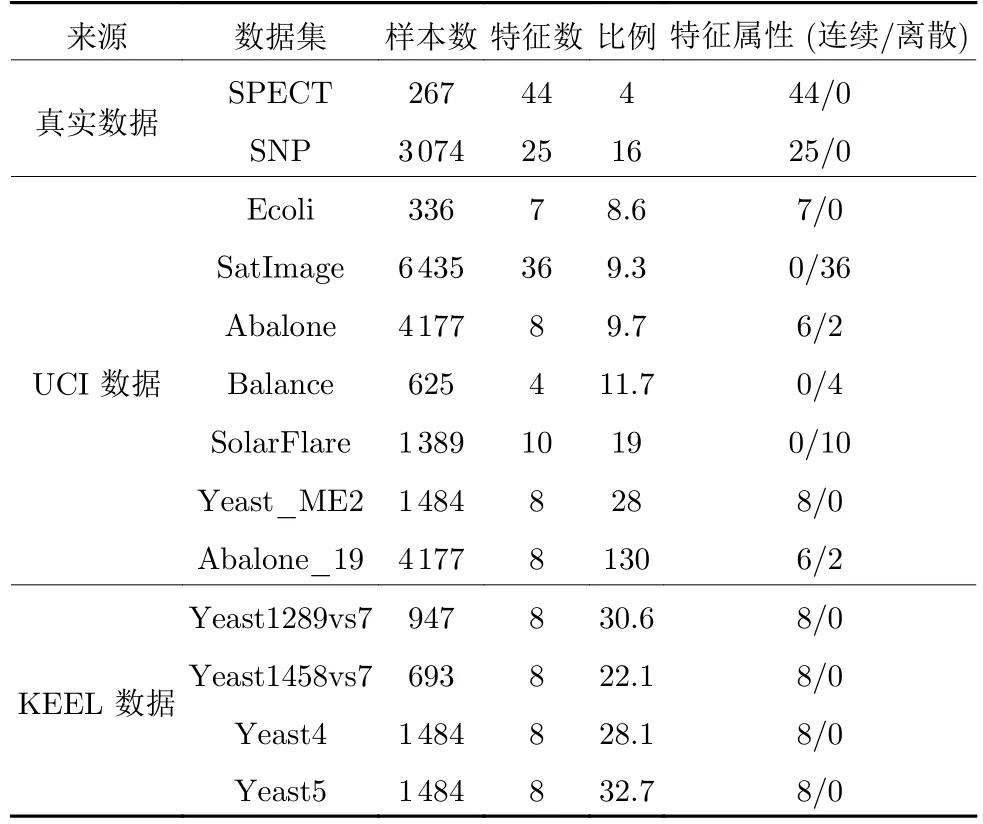
表2 不平衡数据集信息Table 2 Information of the imbalanced dataset

所有数据集用于二分类问题,如果出现多分类数据集,则将其中某一类作为正样本集,剩下的所有类统一合并为负样本集.正负样本数据集的不平衡比例从4 到130 不等,较大的不平衡比例表示正样本集和负样本集之间数量差异较大.

3.2 UCI 数据集

Ecoli 数据集包含35 个少数类和301 个多数类,有7 个特征.该数据是一组蛋白质定位点数据,特征包括氨基酸序列和来源信息,使用这些信息预测蛋白质的定位位点.

SatImage 数据中包含卫星图像3×3 邻域中的像素的多光谱值,以及与每个邻域中的中心像素相关联的分类.通过整合不同类型和分辨率的空间数据(包括多光谱和雷达数据、地图指示地形、土地利用等)对场景的解释预计将具有重要意义.这个数据集中包含626 个少数类和5 809 个多数类,有36个特征.

Abalone 是一个通过物理测量来预测鲍鱼年龄的数据集,物理测量预测鲍鱼年龄是一项既枯燥又耗时的工作,因此使用已有数据进行预测将是更省时的选择.这个数据集包含390 个少数类和3 787个多数类,有8 个特征.

Balance 数据集是用来模拟心理实验结果的,每个例子都被分类为天平的左端、右端或是平衡.属性包括左权重、左距离、右权重和右距离.

SolarFlare 数据集记录了太阳耀斑的数量,每个属性计算24 小时内某类太阳耀斑的数量,每个实例表示太阳上1 个活动区域内所有种类耀斑数量.该数据包含69 个少数类和1 320 个多数类,有10 个特征.

Yest_ME2 数据集是一个酵母菌数据集,用于预测酵母菌蛋白质的定位位点.该数据包含51 个少数类和1 433 个多数类,有8 个特征数.

3.3 真实生物数据

SPECT 数据集是心脏单质子发射计算机断层扫描图像的诊断结果.每个病人被分为正常和异常两类.数据包含对267 个SPECT 图像集(患者)的数据处理结果.提取总结原始SPECT 图像的特征,得到44 个连续特征.在267 个样本中,包含55 个正常病人(少数类)和212 个异常病人(多数类).

SNP 是指在基因组上单个核苷酸的变异,变异形式包括缺失、颠换、变异和插入.在人类基因组中大概每1 000 个碱基就有一个SNP,因此SNP 的数量是相当庞大的.研究表明,SNP 同人群分类,遗传疾病都有密切联系.该数据包含183 个少数类和2 891个多数类,25 个特征.

3.4 KEEL 数据集

本文使用KEEL 数据集的4种酵母菌数据集,原始数据集是一个多分类数据集.在Yeast1289vs7中,将属于VAC 的样本标记为正样本,属于NUC、CYT、POX和ERL 的标记为负样本.Yeast1458vs7属于VAC 的样本标记为正样本,属于NUC、ME2、ME3和POX 的标记为负样本.在Yeast4和Yeast5 中,分别将ME2、ME1 标记为正样本,将其他所有样本均标记为负样本.所有数据集包含8 个特征.

3.5 评价指标

不平衡数据学习的困难不仅体现在分类器的训练上,同时还在于如何客观评价不平衡分类器的性能上.使用总体精度已经不能客观评价不平衡分类器的性能,因为不平衡数据中多数类与少数类具有不同的重要性,对少数类的错误将导致更严重的错误.而总体精度忽略了这一关键因素,即使将结果全部预测为多数类,仍能得到较高总体精度,难以准确反应出分类器在不平衡数据集上的性能.本节介绍本文使用的评价指标,并给出计算公式.

分类性能的评估主要基于混淆矩阵,以二分类为例,表3 展示了其混淆矩阵.TP表示正确预测到的正样本个数,TN表示正确预测到的负样本个数,FN表示正样本预测为负样本的个数,FP表示负样本预测为正样本的个数.

表3 分类混淆矩阵Table 3 The confuse matrix of classification

常见的不平衡数据分类问题评价指标有: 准确率(Accuracy,Acc)、敏感性(Sensibility,Sen)、特异性(Specificity,Spe)、MCC、F-score和Area under curve (AUC),计算公式如下:

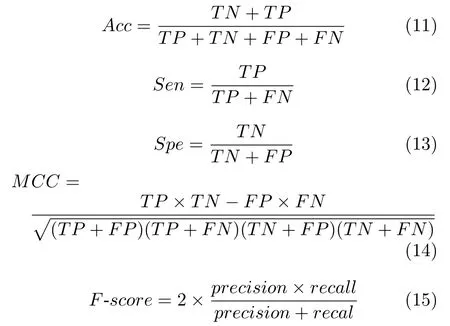
F-score 综合考虑了查全率与查准率,是两者的调和平均数,其值接近其中较小者.在不平衡中,只有当查全率与查准率同时较大时,F-score 才会增大.recall 代表查全率,表示在原始样本的正样本中,最后被正确预测为正样本的概率,计算方法与Sen 相同;precision 为查准率,表示预测结果中,正确预测为正样本的概率如下:

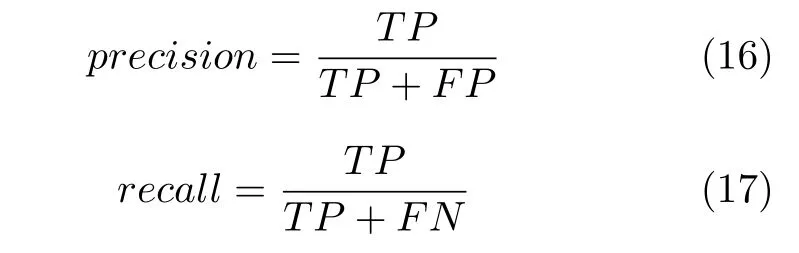
AUC 是Receiver operating characteristic(ROC)曲线下面积,ROC 图由真阳性率(TP-rate)与假阳性率(FP-rate)作图而成,ROC 空间中的任意一个点对应分类器在给定分布上的性能,当真阳性率与假阳性率比值越大时,ROC 就将越接近图形左上角,此时将得到更大的AUC 值,这也意味着分类器结果越理想,AUC 也是评价分类器在不平衡数据上性能的重要指标之一.

4 实验与性能分析

为验证本文方法的有效性,使用13 个数据集进行实验.实验中使用随机森林(Random forest,RF)[33−34]、SVM[35−36]、逻辑回归(Logistics regression,LR)[37−38]和决策树(Decision tree,DT)[39−40]作为分类器.RF 属于Bagging 集成的分类器,由于使用了多个分类器,效果通常好于使用单个分类器.SVM 在处理小样本高维度的数据时有其特有的优势,因为SVM 最终的决策函数由少数支持向量确定,复杂性仅仅取决于支持向量数目而不是原始的样本空间.LR 计算代价不高且容易实现,此外,LR 对数据中小噪声具有一定鲁棒性.DT 算法是一种基于概率的分析方法,在训练时不需要任何领域的先验知识和参数假设,计算量相对较小且准确性高,适合用于高维数据.

在分类器参数选择上,为了最大化突出采样方法自身的特点,参数均使用默认参数设置: SVM 的惩罚系数为1,核方法为径向基函数核(Radial basis function,RBF),gamma 值为1;LR 使用saga作为求解器;DT 使用基尼系数评价特征划分质量;RF 使用具有随机属性选择的决策树作为基分类器,包含50 个独立的决策树,每棵决策树同样使用基尼系数评价划分质量.

为保证训练效果,本文使用5 折交叉验证的方法,将数据集随机分成5 份,每次将其中4 份作为训练集,剩下的1 份作为测试集,重复5 次.最后将5 次实验评价结果的平均值作为交叉验证的结果.所有结果均为5 次5 折交叉验证结果.实验硬件环境为CPU i5-3230m、操作系统为 Windows10、开发语言为Python、集成开发环境为 Pycharm、使用外部库Numpy、Sklearn和Imbalancelearn.

4.1 UCI和真实数据集上分类性能对比

实验设计如下: 首先使用PNS 算法对数据进行预处理,然后分别使用四种不同的分类器对处理后的数据进行训练学习.实验目的是评价不同分类器对不平衡数据的敏感性并为后面实验选择合适的分类器提供参考.

在7 个UCI 数据集和2 个真实数据集上的结果如表4 所示.由表4 可以看出,SVM 在SPECT、Abalone、SolarFlare、Yeast_ME2、Ecoli 这5 个数据集的大多数指标上取得最佳值,RF 在Abalone_19、SatImage、Balance和SNP 这4 个数据集的多数指标上取得最佳值.除Ecoli 数据集的Spe指标,Abalone 的Sen指标以及Abalone_19的AUC指标以外,其余最高值均出自SVM与RF.因此相比LR与DT,SVM与RF 具有更好的分类效果.这说明SVM与RF 对不平衡数据更具有鲁棒性.

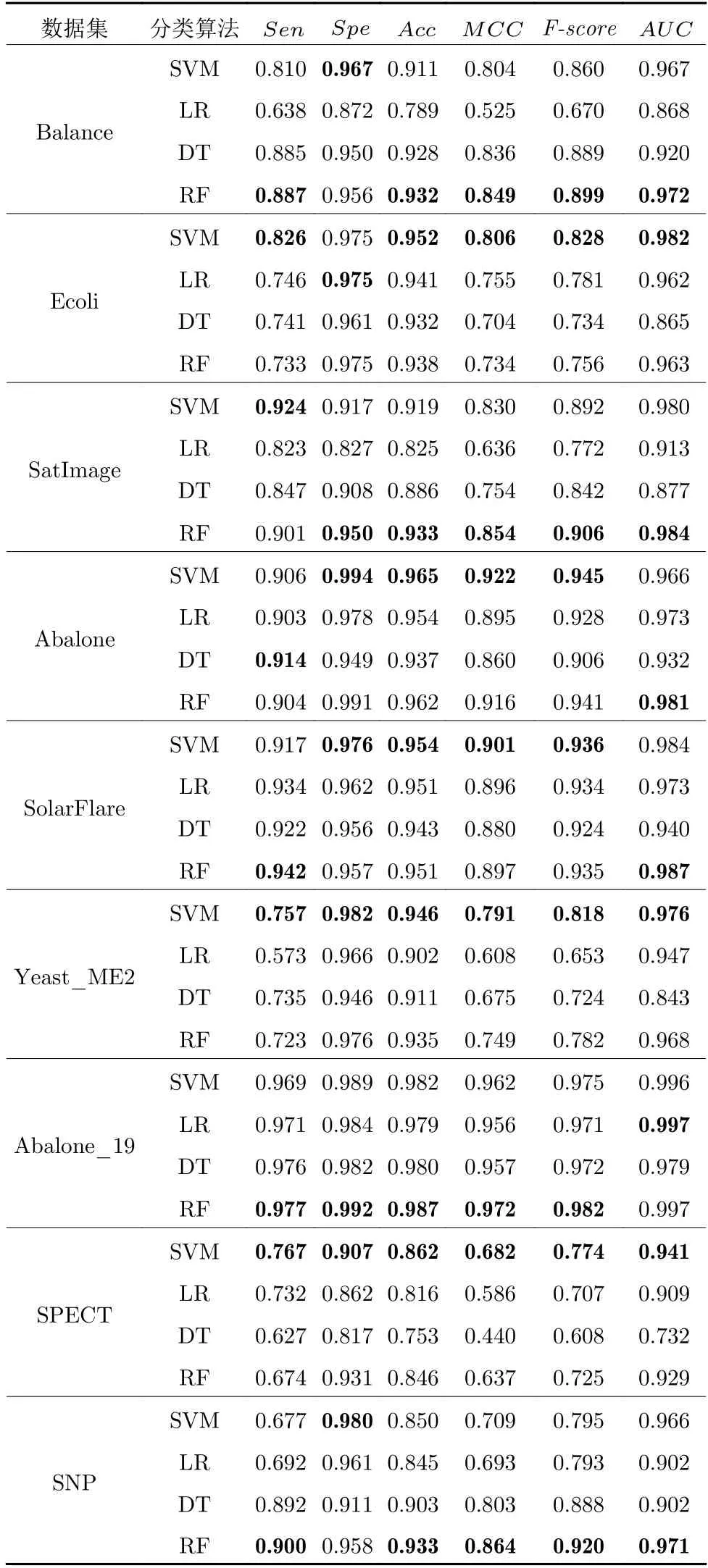
表4 伪负样本采样在分类器SVM、LR、DT、RF上的结果Table 4 Results of pseudo-negative sampling on classifiers including SVM,LR,DT and RF

RF 使用了决策树的集成方法,并且随机森林中每棵决策树的特征选择具有一定随机性,这增大了决策树间的差异,从而使集成效果更好,因此RF 的结果要优于DT,集成方法也是解决不平衡的重要方法之一.SVM 使用核方法将数据映射到高维空间进行划分,而且SVM 的超平面只与支持向量有关,与离决策超平面的数据的多少并不重要,因此使得SVM 对不平衡本身并不十分敏感.LR 在预测时会考虑所有样本点到决策平面的距离,虽然使用了非线性函数进行映射,但也无法很好消除其影响,因此,容易受不平衡影响.

由数据集与分类器的特点可以知道,SVM 趋向于在小样本量的不平衡数据集上具有更好的效果,而RF 趋向于在大样本量不平衡数据集上表现更佳.这也恰恰符合SVM与RF 在平衡数据集上的表现,这说明PNS 算法已经将原始的不平衡数据有效采样成了更平衡的数据,起到了平衡数据集,提高分类器性能的作用.

4.2 采样方法分类性能比较

根据第4.1 节实验结果,本节使用的分类器是支持向量机(SVM)和逻辑回归(LR),因为它们对不平衡数据集具有不同敏感性,SVM 对不平衡数据不敏感而LR 对不平衡较为敏感,如果PNS 算法在这两个分类器上都表现良好,那么可以推断出PNS 算法对大多数分类器均具有较好的提升效果.

实验设计如下: 由于伪负样本采样无需指定采样比例,会根据数据集自适应确定采样比例,因此本文对比相同采样比例下各采样方法的性能.首先使用伪负样本采样方法对原始数据进行采样,得到平衡后的比例,然后按照平衡后的比例使用对比算法重新对原始数据进行采样得到采样结果,最后使用5 折交叉验证对采样数据集进行评价,并重复5次试验取平均值.在对比实验中,将本文提出的PNS 算法与4种数据采样方法进行对比.对比算法包括ROS、RUS、SMOTE和ADASYN.结果如表5所示.

由表5 可以看出,PNS 算法具有最好的综合性能.F-score、MCC和AUC 被认为是在类别不平衡情况下的综合评价指标.它们综合了正样本正确率和负样本正确率,能客观评价不平衡分类器的性能.在这3 个指标上使用SVM 分类器时,算法在SPECT、Ecoli、SatImage、Abalone、Balance、Solar-Flare、Yeast_ME2和Abalone_19 数据集上取得了最好的结果.而在SNP 数据集上,则是ADASYN 算法取得了较好的结果,这是因为它们合成的样本扩充了少数类,同时未减少多数类样本,使其有更高的Sen 值,但是与PNS 相比,它们的Spe 值更低,这说明它们是通过牺牲Spe 来提高其他性能指标的.

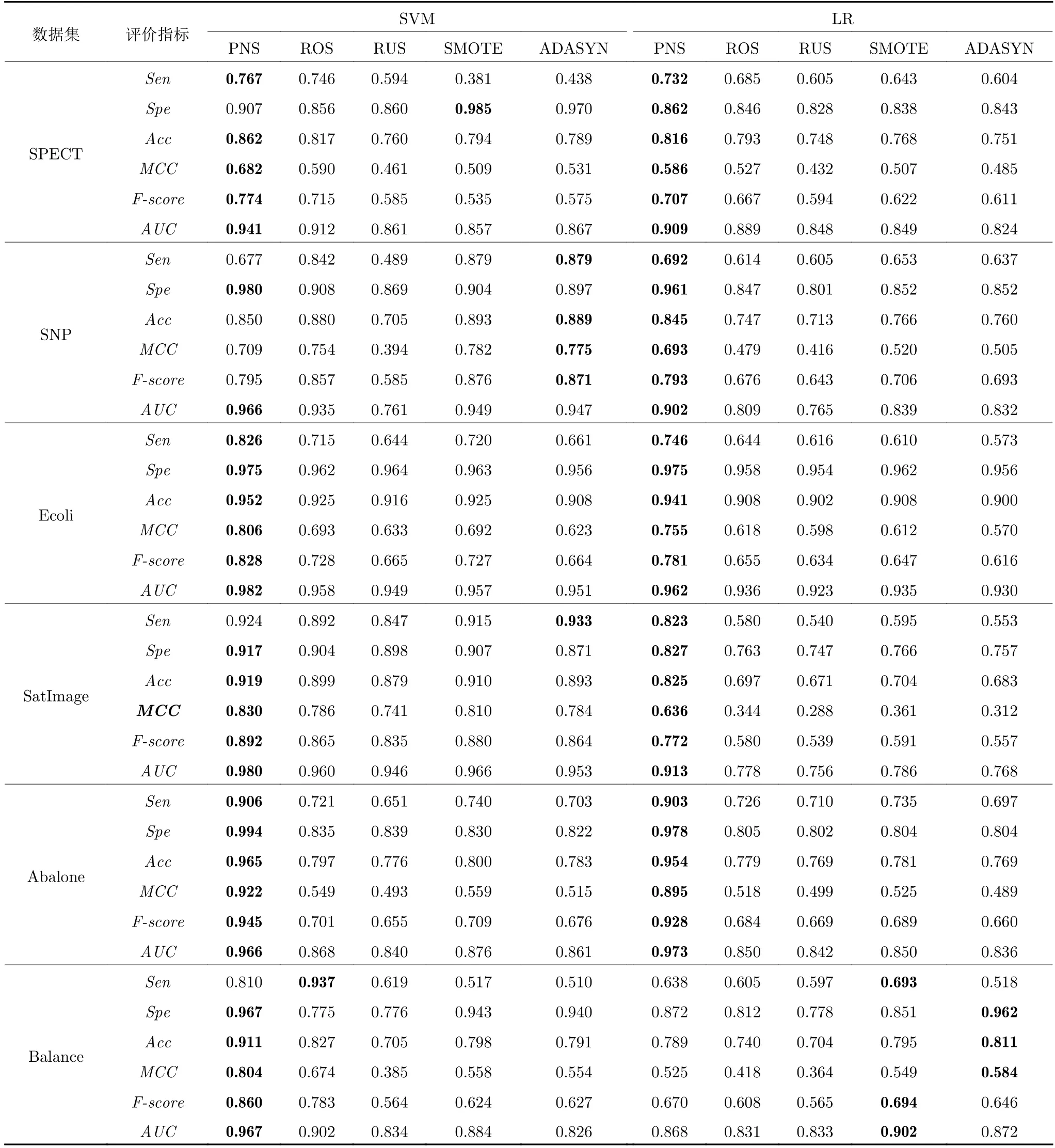
表5 伪负样本采样与ROS,RUS,SMOTE,ADASYN 采样方法对比结果Table 5 Comparison of pseudo-negative sampling with the methods of ROS、RUS、SMOTE、ADASYN

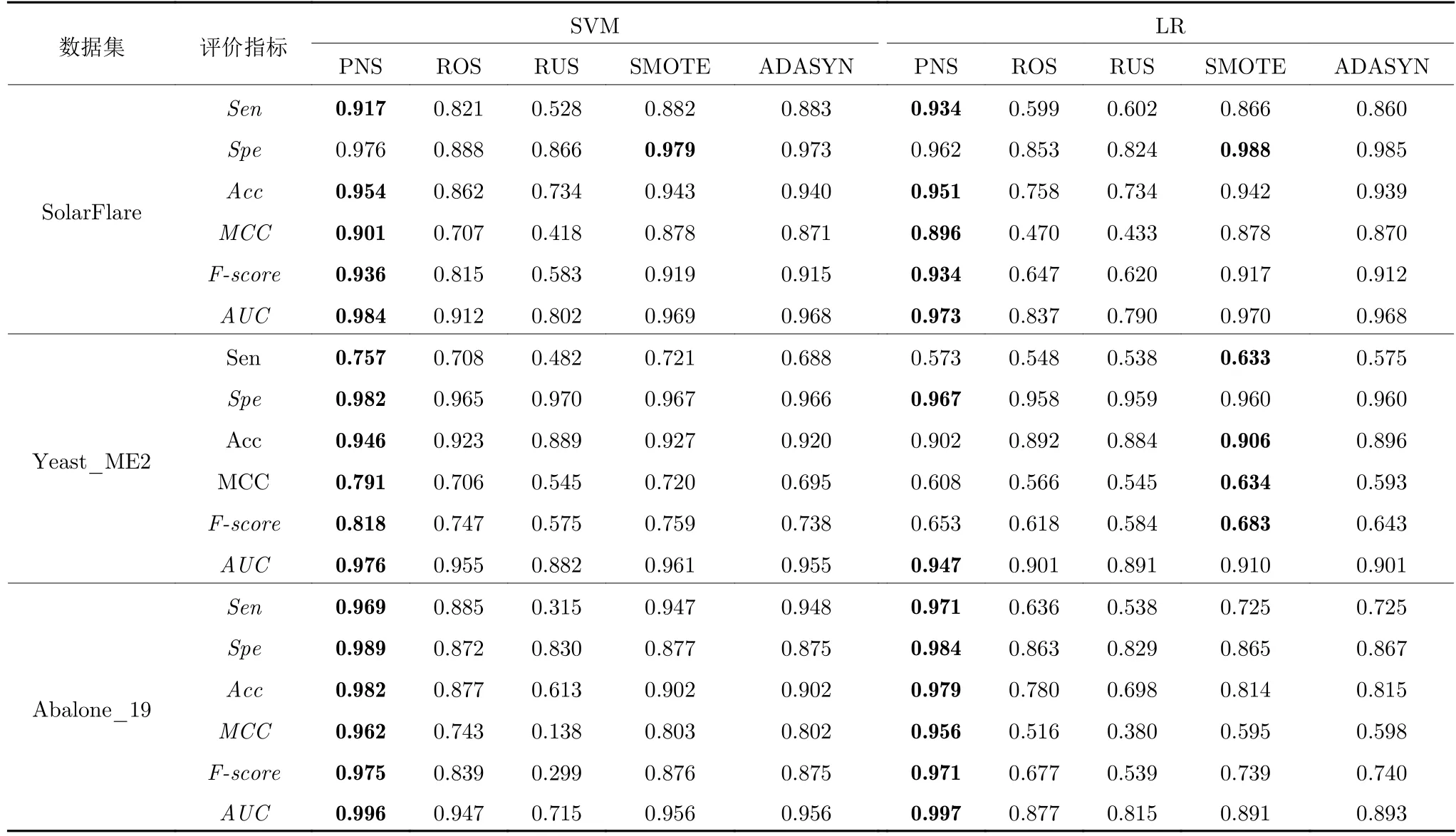
表5 伪负样本采样与ROS,RUS,SMOTE,ADASYN 采样方法对比结果 (续表)Table 5 Comparison of pseudo-negative sampling with the methods of ROS、RUS、SMOTE、ADASYN (continued table)

当使用LR 分类器时,PNS 算法在SPECT、Ecoli、SNP、SatImage、Abalone、SolarFlare、Abalone_19 数据集上取得了最好的结果.在Balance数据集上分别是SMOTE和ADASYN 算法得到较好结果,这是因为过少的特征数不利于伪负样本的选择,因此无法准确找到所有伪负样本导致数据没有得到很好的平衡,同时LR 分类器对不平衡数据较为敏感.在Yeast_ME2 数据集上所得结果与SVM分类器SNP 数据集结果原因类似.

在不平衡数据集的分类当中,少数类的正确率(即Sen)往往受到更多重视,因为少数类通常受到更多关注而Sen 则反映了分类器发现少数类的能力.在Sen 指标下,PNS 采样算法在SVM 的6 个数据集和LR 的7 个数据集上取得最好结果,这表明本文提出的算法对少数类具有很强的辨别能力.从侧面也证实了,分类正确率作为不平衡数据分类的评价指标有时并不能有效地衡量分类器的分类效果.

图2 给出了4 个数据集在SVM 分类器下不同采样方法的ROC 曲线.由图可知,PNS 采样算法在4 个数据集上拥有更好的ROC 曲线,曲线下面积均大于其他采样方法,证明了该方法的优越性.

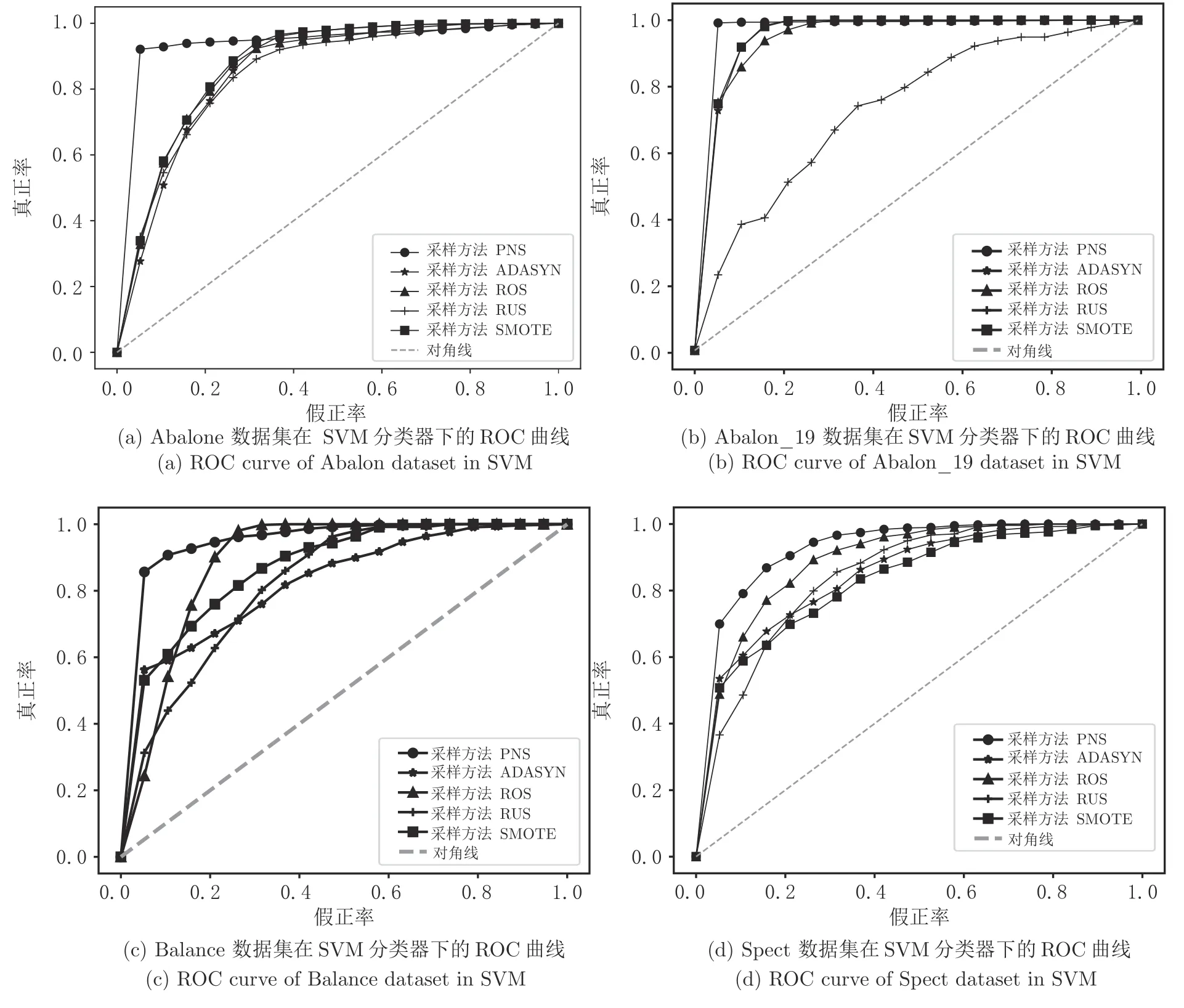
图2 4 个UCI 数据集在SVM 分类器下的ROC 曲线Fig.2 ROC curve of four UCI datasets in SVM

综上所述,PNS 采样算法相比ADASYN、ROS、SMOTE、RUS 算法,对数据具有更好的适应性,因为PNS 考虑了数据集的样本分布,从根本上缓解了不平衡数据少数类被忽略的问题,并且在提高少数类正确率的同时,其他指标保持不变,因此从整体上提高了分类器的性能.此外,由于PNS 在对不平衡数据具有不同敏感性的SVM与LR 分类器上取得最好结果,说明了PNS 的采样结果可以适用于多数分类器.

4.3 高不平衡比例数据对比分析

本节选择不平衡比例大于20 的KEEL 数据,将所提出的PNS 方法与ROS、RUS、SMOTE和ADASYN 进行比较,以验证PNS 采样方法在处理高不平衡数据时的有效性.实验设计思路和所用分类器与第4.2 节相同.实验结果如表6 所示.

由表6 可以看出,PNS 在处理高不平衡数据时,是具有竞争力的方法.与其他4种采样方法相比,PNS 在4 个数据的绝大多数评价指标上取得了最好结果.在只考虑F-score、MCC和AUC 这3 个指标时,PNS 采样在SVM 分类器和LR 分类器的4 个数据集上获得了最好结果.以Yeast1289vs7数据集为例,在SVM 分类器上的F-score、MCC和AUC 值分别为0.909、0.848和0.980;在LR 分类器上的值分别为0.780、0.627和0.902.均优于其他采样方法,这充分说明了PNS 在处理高不平衡比例数据时具有较好的综合性能.在考虑Sen 作为评价指标时,PNS 采样算法在SVM 的3 个数据集和LR 的2 个数据集上得到最好结果.说明PNS 在高不平衡比例数据中依然能很好识别出少数类样本.

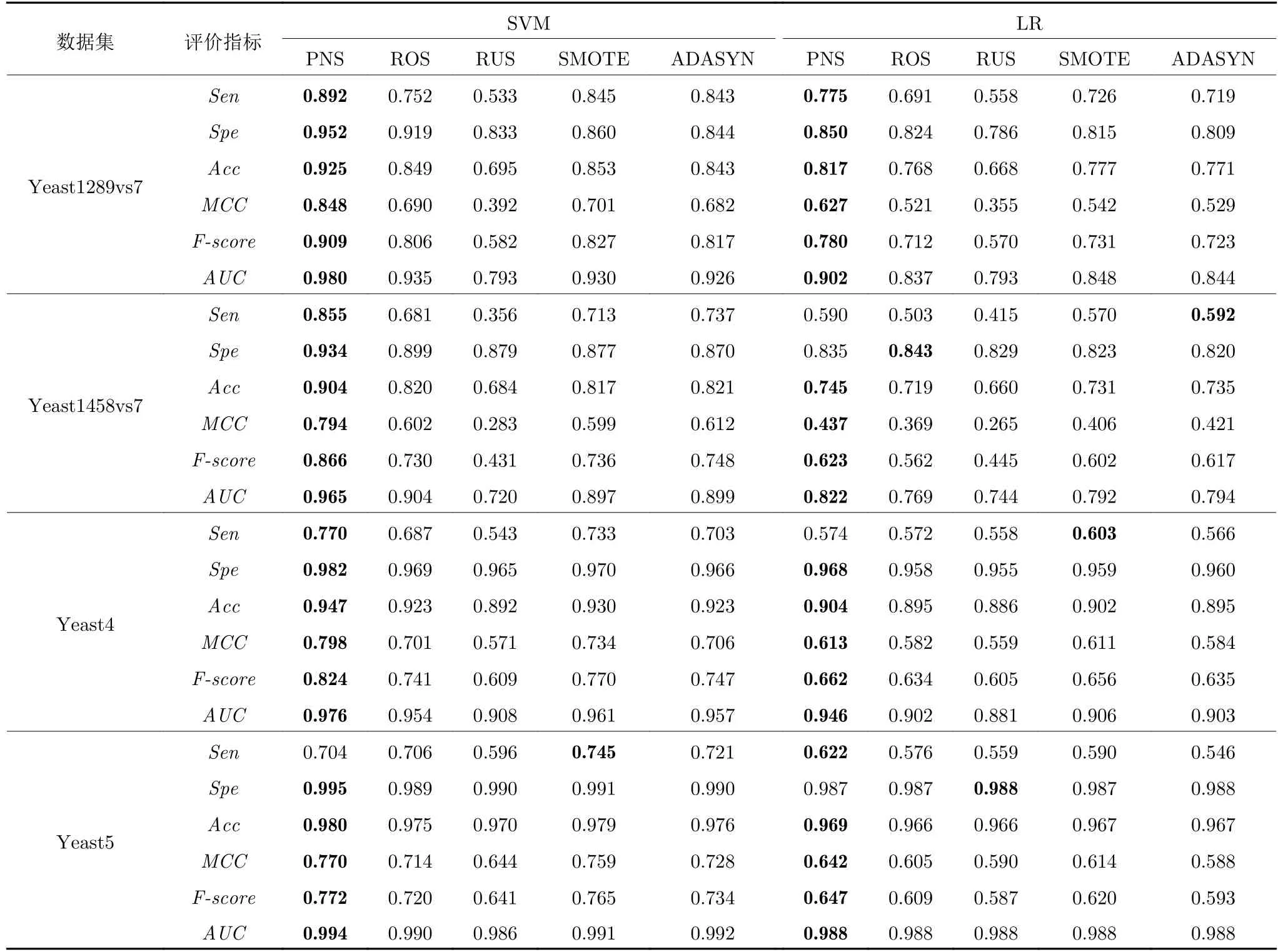
表6 高比例不平衡数据采样对比Table 6 The comparison of high ratio imbalanced data

此外,图3 给出了Yeast1289vs7和Yeast1458vs7两个数据集在SVM 分类器下不同采样方法的ROC曲线.由图3 可知,相较于对比算法,PNS 的ROC曲线拥有更大的曲线下面积,其次是SMOTE、ADASYN和ROS,最后是RUS.由于RUS 移除了大量样本,使得分类器对数据集学习不能很好学习,从而导致欠拟合.SMOTE、ADASYN和ROS 方法生成的样本可能存在噪音或异常值,导致分类效果不如PNS.这说明PNS 不改变数据集样本数量是一种性能更加优秀的采样方法.

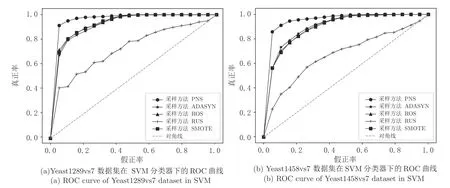
图3 2 个KEEL 数据集在SVM 分类器下的ROC 曲线Fig.3 ROC curve of two KEEL datasets in SVM classifier

4.4 采样方法时间性能对比

本文算法的另一个优势是相对较少的训练时间.表7 展示了不同采样方法在UCI 数据集上的时间消耗对比.

过采样为了平衡数据集会增加少数类样本数量,当正负样本比例越大同时需要越平衡的数据集时,过采样将会生成大量的新样本,这将显著增加训练所需时间,并且大量的合成样本可能导致过拟合现象.同时,相对于欠采样而言,欠采样去掉多数类样本,使训练时间缩短,但是当少数类样本很少时,欠采样往往会删除大部分多数类,这会导致严重的训练不足,分类器无法很好的学习数据,从而使训练效果不尽人意.

相比于上述采样方法,本文所提出的采样方法PNS 则不改变原始样本集的数量,仅改变了数据分布,不会因为引入数据而增加时间成本,也不会删除数据而导致训练不充分,所以具有较好的结果.表7 是各采样方法在不同数据集上使用不同分类器的算法运行时间,每次实验均为5 次5 折交叉验证时间总和,时间单位为秒.

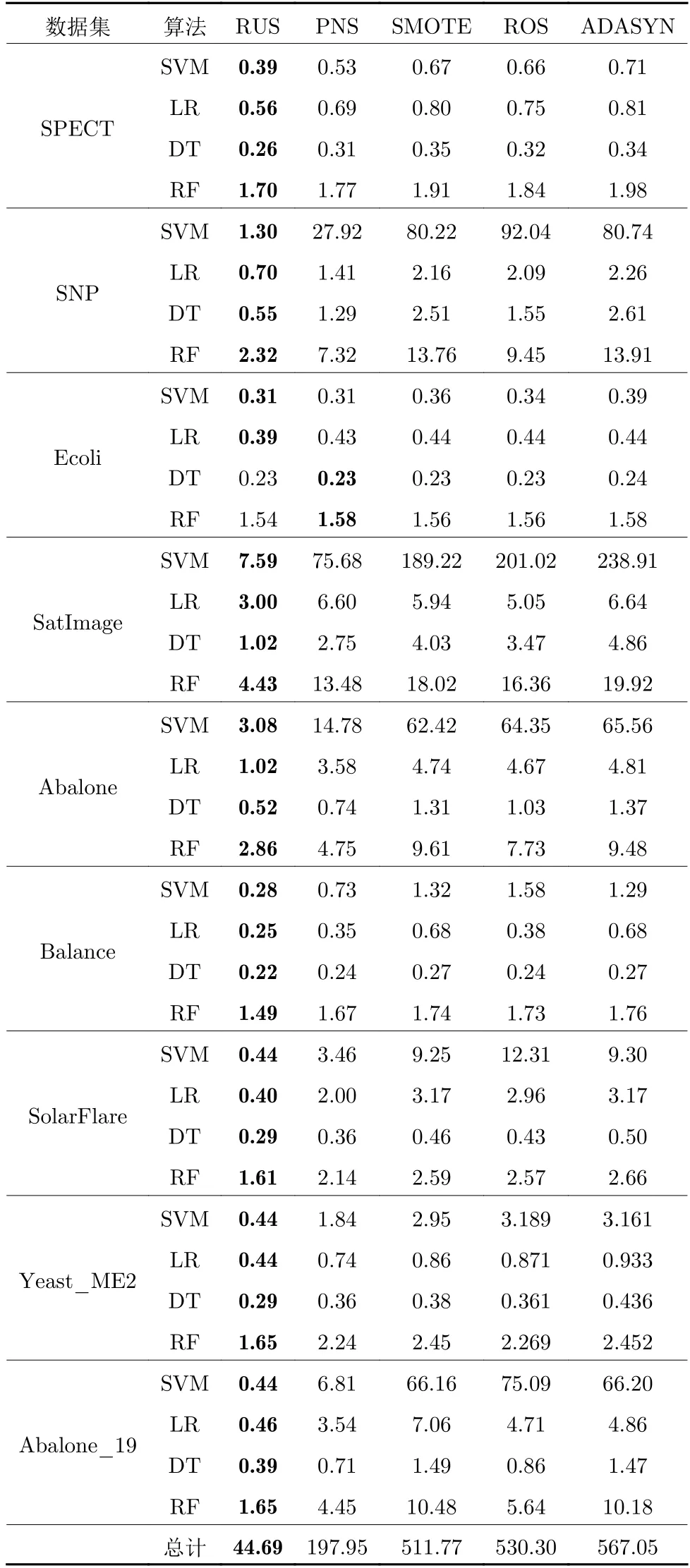
表7 不同采样方法时间对比Table 7 Runtime comparison of different sampling methods

由表7 可以看出,RUS 的总计用时最少,ADASYN的总计用时最多,分别为44.692 秒和567.057 秒.PNS、SMO-TE和ROS 的用时分别为197.954 秒、511.770 秒和530.303 秒.由于同属于过采样,所以ADASYN、S-MOTE与ROS 所用时间处在同一个量级.使用过采样平衡数据时,时间成本的增加在所难免,而随着不平衡比例的增大,时间成本也会相应增大,这不利于处理极度不平衡数据.欠采样虽然减少了时间开销,但是不能得到满意结果.PNS 方法很好地解决了上述问题,在不增加时间成本的同时提高分类器性能,将时间花销控制在可接受范围.

5 结束语

本文提出了一种新型的基于样本空间的不平衡数据采样方法,即伪负样本采样方法PNS.实验结果显示,PNS 采样方法普遍优于其他常用数据采样方法.在不平衡数据集中由于存在大量负样本,使有的负样本与正样本具有相似的分布,与正样本具有很高相似度,可以将其定义为被错分的正样本,基于这一考虑本文提出了伪负样本的概念及其采样方法.具体地,PNS 使用欧几里得距离衡量正负样本间的相似性,将得到的伪负样本从负样本中删除并加入到正样本中.本文方法根据样本的空间分布自适应地对数据进行采样,不需要指定采样比例,具有较强的适应性,避免了采样时选择采样比例的困难.混合采样方法避免了单独使用一种采样方法带来的问题.此外,该算法还具有良好的时间复杂性,采样与训练时间明显少于过采样方法.因此,PNS 采样方法为处理不平衡数据提供了一种可行的新思路.

未来工作包括: 1)将本文提出的伪负样本算法与聚类算法结合[41−43],使用聚类方法获得数据集的更多分布信息,这将有助于提高采样的精准性;2)探索将现有的算法扩展到多分类的任务;3)将算法应用于大规模数据集.