基于自适应反步滑模控制的无人机滚转控制

李 威，田春宝

(沈阳航空航天大学 航空宇航学院，沈阳 110136)

无人机的核心单元是飞行控制系统，该系统可保证无人机在执行任务时自动地调整飞行姿态，是无人机能够安全可靠完成任务的前提。

在目前的自动控制系统中，使用最为成熟，应用最为广泛的控制策略就是PID控制[1]。文献[2]利用MATLAB/Simulink软件对飞机的3个姿态角进行常规PID和串级PID控制仿真。文献[3]使用模糊PID控制器对无人机进行控制仿真。PID控制虽然可以满足大多数的模型，但当遇到较为复杂的非线性无人机模型时，就很难实现稳定控制。文献[4-5]针对高超声速飞行器多变的飞行环境与复杂的自身结构，提出一种基于反步滑模控制理论的控制策略。文献[6]针对复杂结构的变体无人机模型，提出一种基于时变障碍Lyapunov函数的控制策略。文献[7-9]针对飞翼无人机的高度耦合性，提出一系列基于反步理论的控制策略。文献[10-11]针对各自的非线性状态空间模型分别设计了鲁棒自适应控制器以满足控制要求。综上，以反步控制理论、滑模控制理论等为代表的现代控制理论在面向结构复杂、非线性耦合比较强的无人机领域有着很大的发展潜力。

飞行控制系统的设计重点是控制器的设计，本文采用现代控制理论中的反步理论、滑模控制理论、鲁棒控制理论和自适应控制理论针对固定翼无人机滚转通道的稳定控制设计了一系列的控制器。其中核心的控制器是反步滑模控制器，它是反步理论与滑模控制理论有机结合的产物。由于在仿真过程中发现反步滑模控制器存在着强烈的控制输入抖振问题，故在其基础上又分别设计了鲁棒反步滑模控制器、自适应反步滑模控制器用以解决抖振问题，并进行仿真实验。

1 无人机的数学模型与反步控制理论概述

1.1 固定翼无人机滚转通道的数学模型

一般在对无人机进行控制与导航研究时，首先是设计合适的数学模型。由于本文的研究重点是控制器的设计，故在此直接给出无人机滚转通道的状态空间模型。该模型的推导过程与具体参数详见文献[12]。

对滚转角求导得到方程

(1)

式(1)中:φ、θ分别为无人机在机体坐标系的滚转角和俯仰角;p、q、r为无人机的3个姿态角速率;定义dφ1=qsinφtanθ+rcosφtanθ为干扰。

(2)

式(2)中，aφ1、aφ2、dφ2分别为

(3)

(4)

(5)

(6)

(7)

1.2 简单反步控制器的设计方法

简单反步控制器的设计思想是将复杂的非线性系统分解成不超过系统最高阶数的子系统，然后为每个子系统分别设计Lyapunov函数和中间虚拟控制量，一直“后退”到整个系统，直到完成整个控制律的设计[13]。

以二阶反步控制器为例，该控制器的设计步骤一般是先定义角度误差

z1=x1-zd

(8)

其中：zd表示指令信号，再通过角度误差z1构造Lyapunov函数

(9)

图1是反步控制器的设计流程图，当加入滑模控制理论、鲁棒控制理论、自适应控制理论时，仅需要配合其不同的控制理论改变中间虚拟变量z2和后续Lyapunov函数V2与V3的选取即可。

图1 反步控制器设计流程图

2 反步控制器设计

2.1 反步滑模控制器设计

简单反步控制器是只采用反步控制理论设计的控制器，该控制器无法克服扰动[14]。虽然在建模过程中为了方便仿真忽略了许多系统干扰因素，但是在无人机飞行过程中，不确定的干扰仍然非常多。所以此处将反步控制理论与滑模控制理论相结合，设计了反步滑模控制器。这不仅拓宽了简单反步控制器的适用范围，还增强了模型的鲁棒性[15-16]。

(10)

(11)

(12)

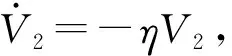
V2(t)=V2(0)e-ηt

(13)

显然，z1和z2指数收敛，且当t→∞时，z1→ 0，z2→ 0，即误差越来越趋近于0，实际值越来越接近目标值。

2.2 鲁棒反步滑模控制器设计

反步滑模控制器无法保证模型的鲁棒性，通过引入鲁棒控制理论，可以克服大部分干扰以保证控制器的鲁棒性，这便是鲁棒反步滑模控制器[17-18]。

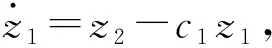
(14)

(15)

式(15)中F=8.661 3+d(t)，可设计控制器

(16)

(17)

取

(18)

有

(19)

2.3 自适应反步滑模控制器设计

无人机系统属于典型的欠驱动、强耦合、非线性系统，在系统运作时常面临外部未知干扰等不确定性，而这些因素都将增加飞行器姿态控制系统设计的复杂性[19]。针对这些不确定性，自适应控制提供了一个有效的解决方案，其优势在于可根据控制系统误差在线更新系统参数，以适应系统内部动态或外界扰动等变化[20-21]。

(20)

设计自适应反步滑模控制器为

(21)

(22)

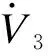
3 仿真分析

使用反步滑模控制器对无人机的滚转通道进行控制仿真，仿真结果如图2～4所示。

图2与图3分别是飞机滚转角度与滚转角速度的跟踪情况。图2表明滚转角的实际值在仿真开始后的0.1 s处与期望值重合，虽然在拐点处出现了误差增加的情况，但是误差的最大值始终没有超过0.01，该控制器的控制效果已经基本满足了需求。图3是实际滚转角速度与期望滚转角速度的追踪曲线，在仿真开始的0.2 s后，两条曲线高度拟合，但是在3 s后实际的滚转角曲线逐渐出现了抖振的现象，这表明控制输入可能在3 s左右产生了较大的抖振。

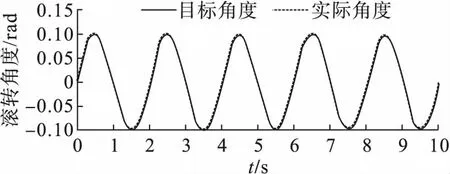
图2 滚转角跟踪

图3 滚转角速度跟踪

图4为控制输入的变化曲线，由图像也可以看出控制输入曲线在仿真开始的3 s之后发生了强烈跳动。这意味着副翼需要在短时间内做出大量的往复运动，即系统会产生强烈的抖振。在实际控制时，应尽量避免该情况发生。

图4 副翼偏转随时间变化曲线

图5是采用鲁棒反步滑模控制器进行控制仿真时，滚转角的跟踪效果图。由图5可以看出,在仿真开始的0.2 s后，两条曲线高度拟合，滚转角控制效果良好。图6显示，在仿真开始0.3 s后滚转角速度的实际值与期望值也基本重合，但是在仿真开始的4 s后又逐渐出现了抖振现象。相较于反步滑模控制器，本次使用的控制器虽然响应时间略长，但在一定程度上减弱了控制输入的抖振。

图5 滚转角跟踪

图6 滚转角速度跟踪

通过观察图7控制输入的曲线变化也印证了抖振问题已经基本解决的猜想，但是在仿真开始的4 s处，系统又有了抖振的趋势，为了解决这一问题，采用自适应反步滑模控制器进行仿真实验。

图7 副翼偏转随时间变化曲线

同样的，假设总的不确定性F(t)=8.661 3-3sin(0.1t)。期望的角度变化取xd=sint，参数h、c1、k1、γ分别取值20、10、15、30，仿真结果如图8～11所示。

图8 滚转角跟踪

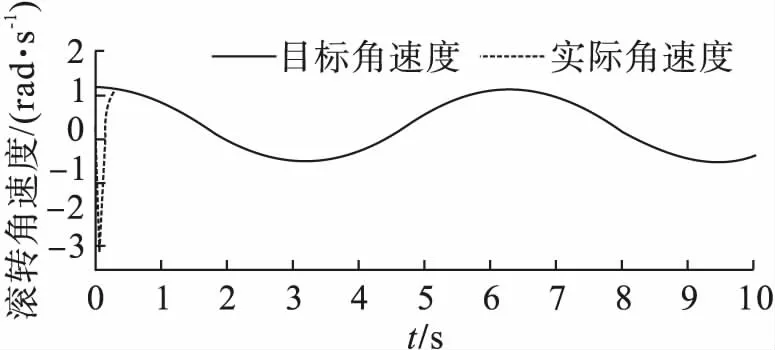
图9 滚转角速度跟踪

图10 副翼偏转随时间变化曲线

图11 估计值的自适应变化曲线

因为自适应反步滑模控制器与鲁棒反步滑模控制器在设计过程中高度相似，所以图8相较于图5并无太大变化。而图9相较于图6而言，前者的实际滚转角速度曲线更加平滑，这表明抖振问题可能已经解决。

4 结论

本文采用3种基于反步控制理论的控制器对固定翼无人机滚转通道分别进行了仿真实验。这3种控制器相较于传统PID控制器而言具有响应时间短、超调量小、控制变量与期望值拟合度高的优点。其中反步滑模控制器的控制输入值不稳定，这可能会导致副翼舵因抖振过大而无法实现稳定控制。在此基础上设计的鲁棒反步滑模控制器在保证控制效果的前提下大幅度减弱抖振，但是随着仿真时间的增加，抖振问题再次出现。最终，在鲁棒反步滑模控制器基础上引入自适应控制理论所设计的自适应反步滑模控制器彻底解决了抖振问题，仿真结果显示该控制器的控制效果良好。