基于Reddy型三阶剪切变形理论的复合材料加筋圆柱壳的屈曲计算

贺 丹,张海波,高艺航

(1.沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室，沈阳 110136；2.国防科技大学 空天科学学院，长沙 410003；3.北京宇航系统工程研究所，北京 100076)

纤维增强复合材料加筋圆柱壳具有高比强度、比刚度、耐腐蚀等优点，常常作为主承力构件应用于航空、航天、船舶等领域。在工作状态下，此类结构往往需要承受严苛的轴压和侧压载荷。因此，在设计过程中，需要准确评估复合材料加筋圆柱壳的抗屈曲/失稳能力。

板/壳变形理论通常可分为经典理论[1]、一阶剪切变形理论[2]和高阶剪切变形理论[3]。经典理论基于Kirchhoff-Love[4]直法线假设，完全忽略了横向剪切变形。Pagano[5]采用经典层合板理论和三维弹性理论分析了层合板的圆柱弯曲问题。结果表明：对于中厚板经典理论预测的精度非常低。这是因为层合板横向剪切刚度小，导致了剪切变形较大而不能忽略[6]。一阶剪切变形理论考虑了横向剪切变形，但假定其不沿厚度方向变化，因此不满足自由表面条件，且需要人为引进剪切修正系数来调整剪切刚度。这种修正并不总是有效的，特别是对于具有高面芯刚度和厚度比的夹层板/壳结构[7]，要提高厚板的计算精度，采用高阶理论是非常必要的。

早期的板壳模型大都是基于经典理论建立的。Dong等[1]基于经典理论研究了复合材料薄壳轴对称弯曲问题。Jones[8]在经典板壳理论的框架下，建立了由拉压不同模量材料构成的复合材料加筋圆柱壳的屈曲模型。孙国钧[9]基于经典理论分析了复合材料加筋圆柱壳的屈曲和初始后屈曲。Bich等[10]基于经典板壳理论推导了加筋圆柱壳的控制方程，获得了偏心加筋FGM圆柱壳的非线性动力分析结果。Thang等[11]基于经典板壳理论研究了弹性地基上受轴向压缩的S-FGM环壳段的非线性动力屈曲。肖汉林等[12]基于经典板壳理论导出了加筋圆柱壳的动力控制方程，采用Rayleigh-Ritz法求解出加筋圆柱壳的自由振动频率。

为了提高中厚板壳的计算精度，学者们在一阶剪切变形理论方面开展了许多工作。Reddy[2]基于一阶剪切变形理论研究了简支双曲正交铺设层合壳在正弦、均布和中心载荷作用下方程的精确解,给出了正交铺设层合壳的基本频率。肖汉林[13]基于一阶剪切理论研究了复合材料加筋圆柱壳在轴压作用下的稳定性问题。朱菊芬等[14]基于一阶剪切理论研究了层合板壳脱层屈曲及后屈曲问题。王天霖等[15]基于一阶剪切理论研究了径向载荷作用下复合材料圆柱壳的动力响应问题。Sadeghifar等[16]基于一阶剪切变形理论推导了复合材料加筋圆柱壳的控制方程，采用Rayleigh-Ritz法计算了临界屈曲载荷。王震鸣等[17]基于一阶剪切变形理论研究了加筋圆柱曲板的稳定和振动问题。Shen[18]利用奇异摄动法研究了正交圆柱壳在外压和轴向压缩联合作用下的临界屈曲载荷和后屈曲平衡路径。

高阶理论能够进一步改善中厚板壳尤其是厚板壳的计算精度，因此一直是板壳理论领域的研究热点之一。高阶理论可细分为等效单层高阶理论[19-21]和分层理论[22-23]两类。分层理论假设每一层有独立的位移场，提供了足够的贯穿厚度的运动自由度，并允许在某些情况下，强制横向剪应力沿着厚度保持连续[24]。这种理论的计算精度较高，缺点是引入了更多的未知数，增加了求解的成本。Barbero等[25]提出了层合壳分层理论，并用此理论研究了层合壳的振动问题，给出了简支圆柱壳线性方程组的精确解。Reddy等[26]利用分层理论研究了简支端部条件下环向和轴向加筋复合材料圆柱壳的屈曲问题。Wu等[27]基于Li等[28]提出的整体—局部叠加技术提出了一个整体—局部高阶层合壳模型，用于预测层合壳厚度的位移和应力分布。郭凡增等[29]基于整体局部高阶剪切理论研究了复合材料层合板的静力问题。等效单层高阶理论假定剪切变形沿厚度方向呈高次曲线分布，可以满足自由表面条件，也不需要引入剪切修正系数，且未知数的个数与一阶理论相同。Matsunaga[30]提出了多项式高阶理论并应用于正交铺层复合材料扁壳和圆柱壳[31]的振动和稳定性分析。陈荣庚等[32]基于高阶剪切变形理论建立三角形精化板单元，研究了复合材料层合板的静力弯曲问题。Reddy建立了一种三阶剪切变形理论，其计算精度在如挠度、自振频率以及屈曲等整体性的响应方面与分层理论的精度相当，但局部响应如层间应力等响应则差强人意。因此，在分层理论的高精度和一阶剪切理论的低计算成本之间，Reddy三阶理论可以作为一种折中的选择。沈慧申[33]基于Reddy型高阶剪切理论研究了复合材料曲板在侧压作用下的后屈曲问题。何煌[34]采用Reddy型高阶剪切理论研究了含有初始几何缺陷的编织复合材料圆柱壳的屈曲问题。

综上所述，加筋圆柱壳屈曲问题的研究经历了从经典/一阶理论到高阶理论、从光筒壳到加筋壳的过程。对于铺层数较多或厚度较大的复合材料结构来说，采用高阶理论能显著提高计算精度。目前基于高阶理论研究层合板的工作较多，但针对加筋壳体的工作较少。本文将Reddy型三阶剪切层合板理论推广至复合材料加筋圆柱壳屈曲问题，在保持较少未知数的情况下，新模型所预测出的屈曲载荷与经典/一阶理论相比具有明显的精度优势。

1 基本方程

1.1 蒙皮的位移及应变

根据Reddy型三阶剪切变形理论，壳体的位移场可以表示为z坐标的3次函数，如图1所示。

图1 层合双曲壳的几何形状

(1)

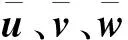
层合壳的横向剪切应变可以表示为

(2)

式(2)中：ε4、ε5为横向剪应变。

将式(1)带入式(2)可得

(3)

考虑到剪应变在壳体的上下表面为零，可得

(4)

式(4)中：h为壳体的厚度。

将式(4)回代到式(1)，得到层合壳的位移场

(5)

再由几何方程可以得到壳体的应变场

(6)

为采用高阶理论所得到的应变。

1.2 蒙皮的本构方程

蒙皮中第k层的本构关系可表示为

(7)

其中：

式(7)中：E1、E2分别为第k层沿着纤维和基体的弹性常数；G12、G13、G23为第k层的剪切模量；ν12、ν21为材料的泊松比。

1.3 加强筋的位移、应变及本构

加强筋通常采用单向铺层，横向剪切效应不显著，可将其视为Euler-Bernoulli梁。

轴向加强筋的位移场可以表示为

(8)

环向加强筋的位移场可以表示为

(9)

式(8)、(9)中：(us,ws)、(vr、wr)分别表示轴向筋条和环向筋条的位移;u1、v1、w1为加强筋与壳体表面接触的点的位移分量。

加强筋的应变表示为

(10)

加强筋采用单轴应力-应变方程

(11)

式(10)、(11)中：(εs,σs)、(εr,σr)分别表示轴向和环向加强筋的应变和应力。

2 能量原理与控制方程

2.1 壳体的内力虚功

结构蒙皮的内力虚功可表示为

(12)

其中

(13)

2.2 加强筋的内力虚功

轴向加强筋的内力虚功为

(14)

环向加强筋的内力虚功为

(15)

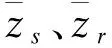
具有轴筋和环筋圆柱壳的几何形状如图2所示。

外载荷所做的虚功为

(16)

加筋圆柱壳的总的内力虚功为

δUtotal=δUskin+δUs+δUr

(17)

由虚功原理有

δUtotal=δV

(18)

其中：δUtotal为加筋圆柱壳的总内力虚功。

图2 加环筋和轴筋圆柱壳的几何形状

2.3 加筋圆柱壳的控制方程

从式(18)经过分部积分可导出复合材料加筋圆柱壳的控制方程

(19)

3 算例分析

本节首先考虑了受侧压作用的两端简支的金属加筋圆柱壳，通过将计算出的临界屈曲载荷与文献结果进行对比，证明了本文结果的准确性；其次考虑了受轴、侧压作用的复合材料圆柱壳，特别注意考察在不同的厚径比下，本文结果与一阶剪切结果之间的差异；最后研究了复合材料加筋圆柱壳，讨论了不同的加筋方式以及厚径比等参数对临界轴压/侧压屈曲载荷的影响。

算例1

首先考虑比较薄的、受侧压作用的两端简支的各向同性加筋圆柱壳，其几何和材料参数如下[35]

h/R2=0.0121 7,L/R2=4.539 1,As/Ssh=Ar/Srh=0.147 1,Ir(Srh3/12)=Is(Ssh3/12)=0.781 9，zr/h=±1.653,zs/h=±1.653,E=30×106psi,ν=0.3,R1=∞,R2=82.169,Nr=516,Ns=373

根据边界条件，试函数可取为

(20)

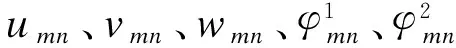
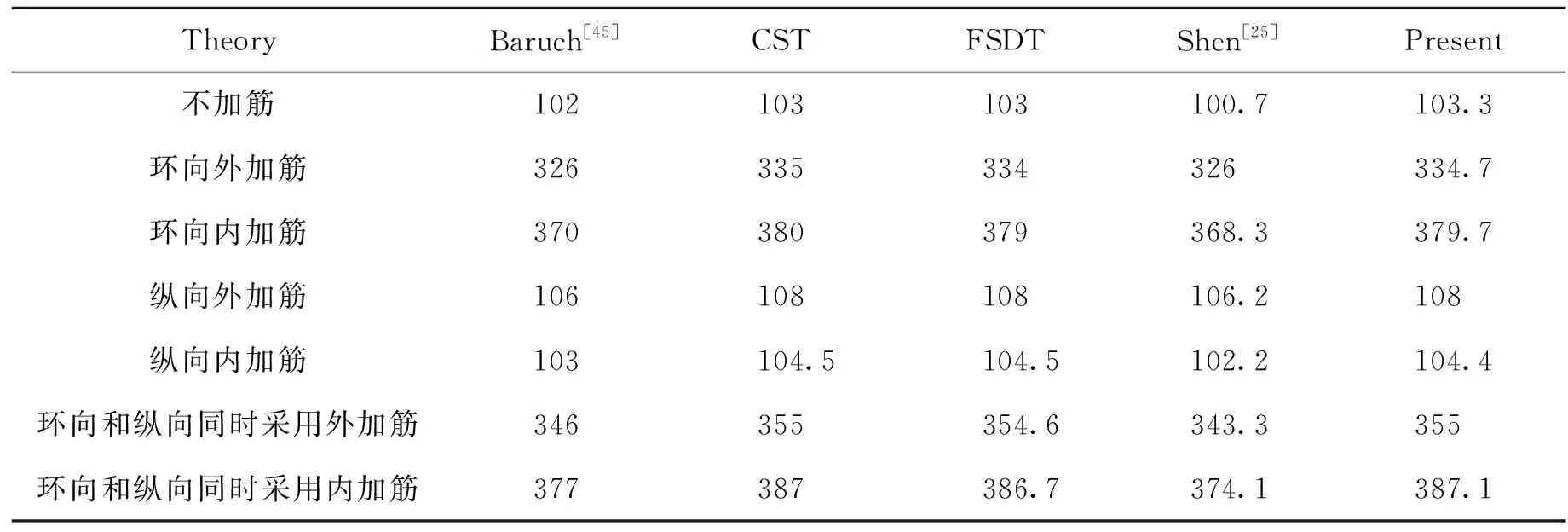
表1 各向同性圆柱壳不同加筋结构本模型与参考文献侧压屈曲荷载结果的对比 lb/in2

算例2

考虑分别受轴压、侧压作用的两端简支复合材料圆柱壳(0°/90°/0°)，其材料和几何参数为[36]

E2=1GPa,E1=40E2,G12=G13=0.6E2,G23=0.5E2,ν12=ν13=0.25,R1=∞,R2=1m

图3给出了临界轴压屈曲载荷随厚径比(半径为常数)变化的趋势。从图3可以看出，在径厚比较小时，本文结果与FSDT的结果趋于一致；当厚径比逐渐增大时，二者出现明显的分歧，如当h/R2=0.3时，FSDT模型相对于本模型的误差可达9.8%。图4给出了侧压临界屈曲载荷随径厚比变化的趋势，与轴压类似，本文模型所预测出的结果总是低于FSDT的结果，且径厚比越大差异就越明显。这是因为FSDT假设面内位移沿厚度为线性变化，人为增加了结构的刚度，而本文模型用三阶函数描述面内位移，因此更加贴近实际情况。所以，有理由认为随着圆柱壳厚径比的增大，本文模型能够取得比FSDT更精确的解。

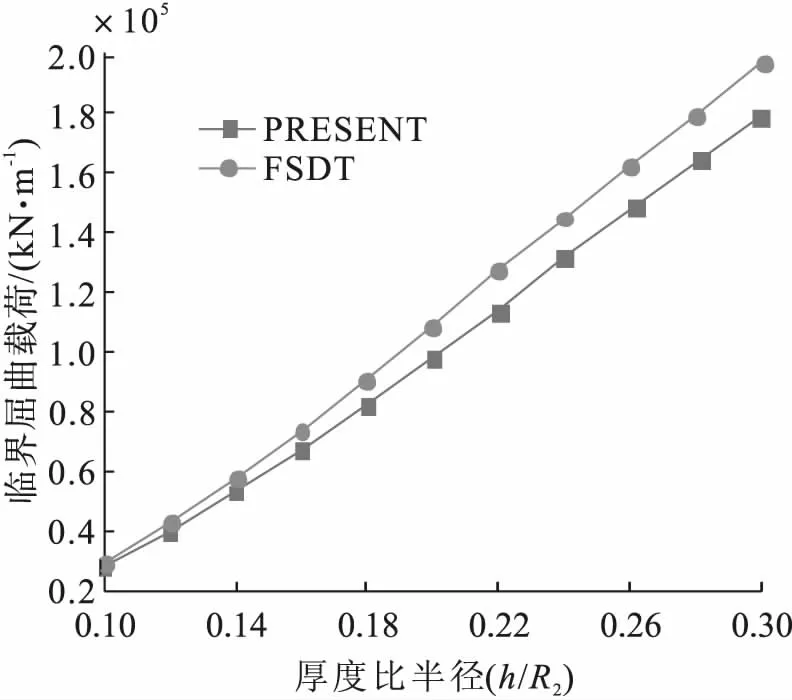
图3 简支层合圆柱壳轴压屈曲临界载荷随壳厚径比的变化

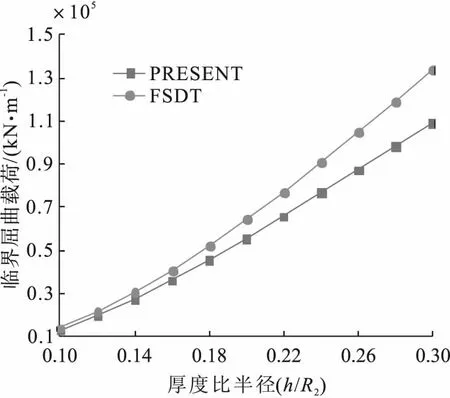
图4 简支层合圆柱壳侧压屈曲临界载荷随壳厚径比的变化

算例3

考虑两端简支的复合材料加筋圆柱壳，分别研究其在轴压和侧压作用下的屈曲问题。结构中环筋与纵筋的材料和截面属性相同，各组分的几何和材料参数如下：E2=1 GPa，E1=40E2，G12=G13=0.6E2，G23=0.5E2，ν12=ν13=0.25，R1=∞，R2=1m，bs=0.1，ds=0.1，Ns=10，L=1m，Nr=10，Ss=2πR2/Ns，Sr=L/Nr，Es=20E2，v=0.3

表2给出了不同加筋形式及不同厚径比下结构的临界轴压屈曲载荷。不难看出，对于承受轴向载荷的加筋壳而言，纵向加筋的效率高于环向加筋，但无论是纵加筋还是环加筋，筋条布置在结构外侧总是更有优势。另外，无论加筋形式如何，当蒙皮较薄时FSDT解与本文解较为接近;而当厚径比增大时，二者的分歧愈加明显。如当厚径比为0.3时，对于纵向加筋圆柱壳，本文解与FSDT解之间的分歧可达约5.7%；对于环向加筋圆柱壳，本文解与FSDT解之间的分歧可达约6%。

表3给出了不同加筋形式及不同厚径比下结构的临界侧压屈曲载荷。不难看出，侧压工况下，环向加筋的效率要高于纵向加筋，外加筋的效率要略高于内加筋。特别值得注意的是，在侧压工况下，本文解与FSDT解之间的分歧更加显著。如当圆柱壳采用轴向加筋时，在蒙皮较薄即厚径比为0.1时，本文解与FSDT解之间分歧约为6.2%；而当厚径比为0.3时，二者间的分歧可达23.2%左右。当结构采用环向加筋时，二者间的分歧稍小一些，但在厚径比为0.3时，也有约4.5%的分歧。

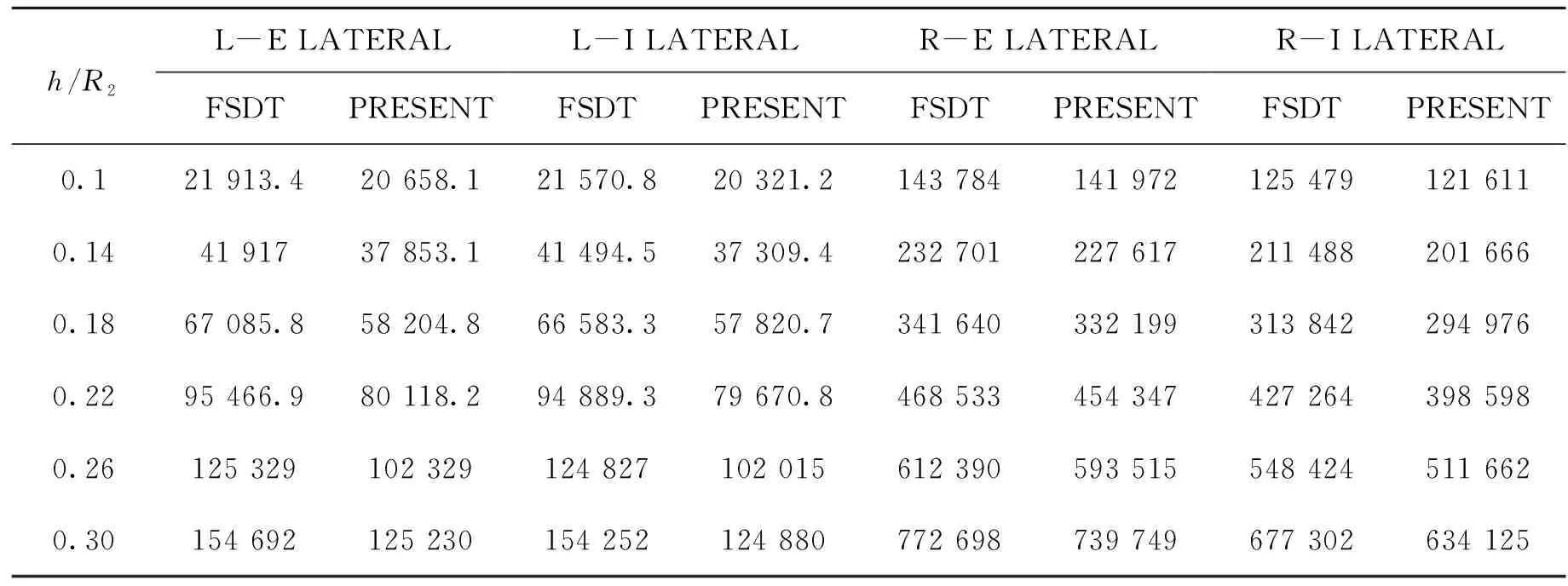
表3 轴向和环向内外加筋侧向压缩临界屈曲载荷 kN/m2

4 结论

本文将Reddy型三阶剪切层合板理论推广至复合材料加筋圆柱壳屈曲问题。基于能量原理建立了屈曲控制方程，并通过算例分析证明了本文结果的准确性，讨论了不同设计参数下本文解与经典FSDT解之间的异同。得到的主要结论为：

(1)对于提高结构承载能力而言，外加筋总是要好于内加筋，尤其是当结构承受轴向载荷时更是如此；

(2)纵向加筋更有利于提高轴压承载能力，环向加筋更有利于提高侧压承载能力；

(3)当蒙皮较薄即径厚比较小时，本文解与经典FSDT解较为接近，但是当径厚比增大时，二者间的分歧非常明显；

(4)考虑到本文模型比FSDT模型具有更高的面内位移阶数，从而更加贴近实际情况，因此有理由认为本文解具有更高的精度，对于较大径厚比的结构以采用本文模型进行屈曲计算为宜。