基于Co-Kriging代理模型的扇形冷却孔结构优化

陈 萍，左 宁，王泽轩，齐婷婷,于明月

(沈阳航空航天大学 a.民用航空学院,b.自动化学院，沈阳 110136)

随着航空发动机技术日益精进，推重比不断提高，涡轮进口温度也随之提高。英国“先进核心机军用发动机”(ACME)的研究表明，推重比达到20，涡轮进口温度将提高到2 403 K。要达到这一目标，确保发动机在如此高温下能够正常工作，涡轮叶片等热端部件的冷却技术研究至关重要。国内外学者主要从2个方向进行了深入研究，一方面是提高材料的耐热性，发展高性能耐热合金。通过材料的改善，涡轮叶片的冷却性能提高了40%；另一方面是采用高效的冷却技术使涡轮叶片的冷却性能提升到60%[1]。其中，气膜冷却是通过叶片表面的小孔，将冷却介质以射流形式注入主流，与叶片表面形成薄膜，对壁面进行保护[2]，是航空发动机热端部件的主要冷却方式之一。

扇形气膜孔是最为典型的扩张型孔型，可以有效地抑制在冷却孔下游产生的肾型涡对。文献[3-5]研究了扇形孔的冷却效率，与圆形孔相比，扇形孔具有更高的冷却效率。文献[6-7]指出与圆形孔相比，扇形孔能有效抑制高吹风比下的气膜分离。但扇形孔结构复杂，对冷却效率的影响因素更多。Park等[8]采用响应面法，以前扩张角、后扩张角和孔长作为设计变量，对扇形孔进行了优化设计，结果表明优化后的气膜孔冷却效率提高了52.4%。Wang等[9]采用径向基神经网络和遗传算法对气膜孔进行优化设计，设计变量选择平板扇形孔倾斜角、侧向扩展角和孔长。结果表明在吹风比M=1.5的工况下，冷却效率提高了38.5%。冯红科等[10]采用支持向量机代理模型和遗传算法，对椭圆槽气膜冷却结构优化进行了详细研究，在M=1.2的工况下，冷却效率提高了73%。Gartshore等[11]通过实验研究了冷却孔入口几何形状对扇形孔的冷却效率的影响，结果显示优化后的冷却孔比优化前冷却效率提升了12%。Lee等[12]通过Kriging代理模型和序列二次规划相结合的方法，对扇形孔的4个几何参数进行优化设计，结果发现在M=0.5和M=2.5的工况下，气膜冷却效率分别提高了31.8%和44.9%。与Kriging代理模型相比，Co-Kriging代理模型可以有效利用2种不同可信度数据，更加精确地进行拟合，并大大减少计算时间。

扇形孔气膜冷却性能受扇形结构参数影响较大，如何合理优化扇形结构以获得最优的冷却性能是值得探索的问题。本文以扇形气膜孔出口几何参数作为研究对象进行优化设计，首先提出扇形孔气膜冷却优化模型；在此基础上提出Co-Kriging和遗传算法相结合的扇形孔气膜冷却优化方法；最后针对优化前后的扇形孔气膜冷却流场、温度场进行详细的对比与分析。

1 物理模型与优化方法

1.1 物理模型

如图1所示，计算区域由主流通道、冷气通道以及带扇形孔的气膜孔组成。纯圆柱部分的直径D=10 mm，直孔段孔长Lm与扩张段孔长Lfwd之和为8D，圆柱轴线与气膜孔出口平面的夹角α=35°，后向扩张角β=10°，侧向扩展角γ=10°保持不变。主流通道长为76D，截面尺寸为9D，冷气通道长50D，截面尺寸为7D。

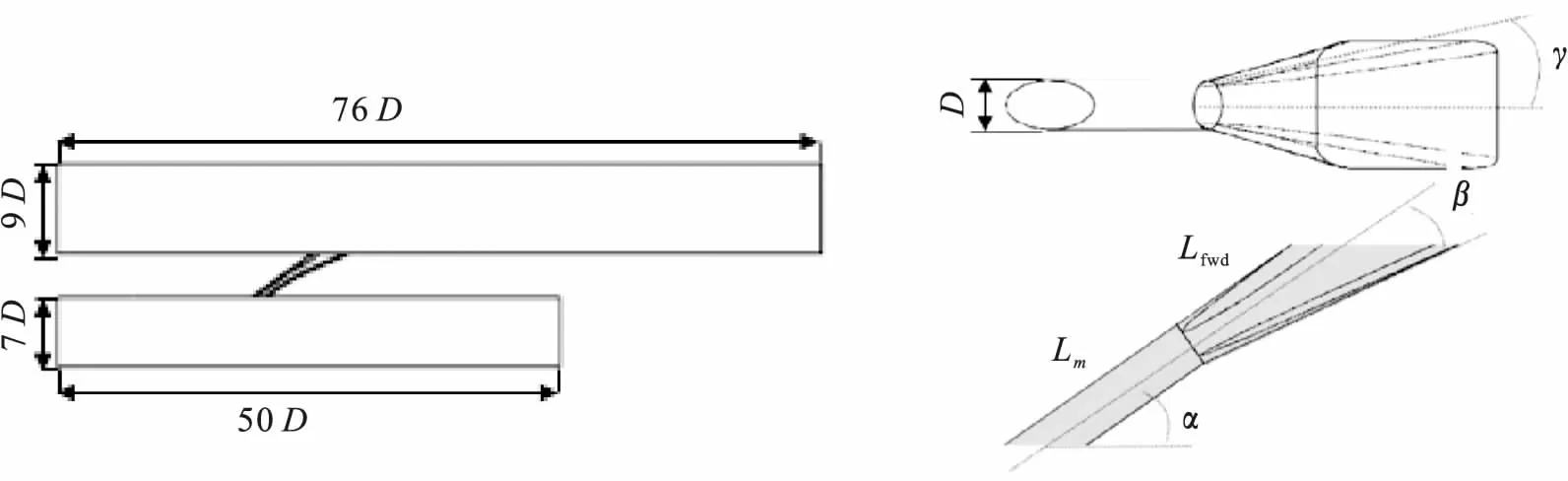
图1 计算模型和扇形孔示意图

1.2 设计变量和目标函数

本文的优化工作在吹风比M=1.5的工况下进行。选取直孔段孔长Lm，前向扩展角α和后向扩展角β作为设计变量，气膜孔设计变量范围如表1所示。以气膜孔下游X/D∈[1,50]区间内平均绝热冷却效率ηavg作为目标函数，ηavg定义为

(1)

ηad=(Τ∞-Τaw)/(Τ∞-Τc)

(2)

式(1)、(2)中:T∞为主流进口温度;Taw为绝热壁温;Tc为冷气进口温度。

优化流程如图2所示，首先确定优化目标函数，在此基础上选择3个设计变量，并确定其范围，针对这3个变量，利用拉丁超立方设计方法进行试验设计，并建立有限元模型，对其进行CFD求解，组成一定容量的样本库；其次构建Co-kriging代理模型并对样本点进行拟合；最后引入遗传算法进行迭代优化，搜寻全局最优设计点，得到最优气膜冷却孔结构。

表1 设计变量

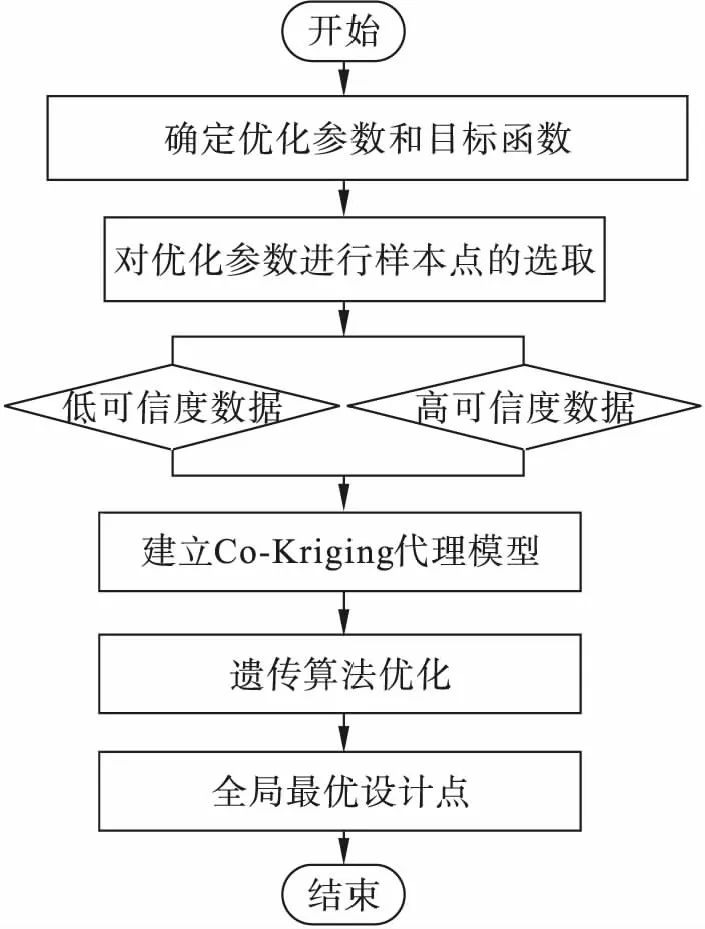
图2 优化流程图

1.3 基于Co-Kriging的优化方法

Co-Kriging代理模型是由多组互不干扰的高、低可信度样本构建而成，与只采用高可信度样本构建Kriging代理模型相比，该方法能降低获取高可信度数据所需要的时间及计算代价[13]。

假定采用低可信度和高可信度两组样本数据，首先取nc个低可信度样本，输出表示为Xc，其响应为Yc；取ne个高可信度样本，输出表示为Xe，其相应为Ye。1个Co-Kriging代理模型可分为2个Kriging代理模型：(1)低可信度代理模型；(2)利用高低可信度数据差值构造的代理模型。用Ze、Zc分别代表高可信度模型和低可信度模型的高斯过程，三者之间存在如下关系

Ζd=Ζe-ρΖc

(3)

式(3)中:ρ为缩放系数。

仿照Kriging代理模型中协方差矩阵的构建，Co-Kriging代理模型的完整协方差矩阵构建如下

(4)

(5)

(6)

(7)

(8)

式(4)～(8)中:ψc、ψd为相关性矩阵。

通过MLE(极大似然估计)方法求得θc、θd，进而求解相关性矩阵ψc、ψd。基于以上两种Kriging代理模型，Co-Kriging方法对高可信度模型的估计为

(9)

相对均方根误差RMSE能较好地说明模型对样本点的拟合程度。范围在0～1，RMSE值越接近0，表明近似拟合的精度越高，其表达式为

(10)

式(10)中：Yi表示响应面模型计算值；yi表示有限元分析结果；y表示有限元分析结果的平均值；n表示设计空间上采样点数量；p表示响应面数学模型中非常数项的个数。

1.4 网格独立性及数据验证

设计5种不同网格质量(50万、100万、150万、200万和250万)，在吹风比M=1.5的工况下对扇形孔进行网格独立性验证。图3为不同网格质量下气膜孔下游平均气膜冷却效率分布。从图3中可以看出，当网格数量增加到250万时，气膜平均冷却效率基本不变，因此确定网格节点数为250万。

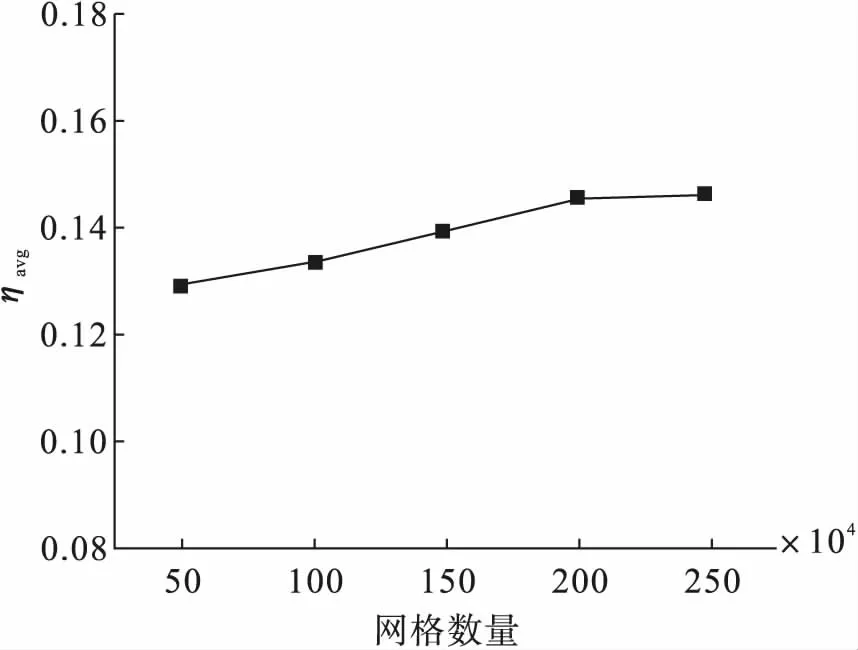
图3 网格无关性验证

图4为50万网格、250万网格和实验数据在不同吹风比下，平均冷却效率与实验数据对比，在吹风比M=1.5的条件下50万网格计算的数值和实验数据有8%的误差，而250万网格计算的数值和实验数据仅有3%的误差。综上，在50万网格下计算得到的数据作为低可信度数据，在250万网格下计算得到的数据作为高可信度数据。

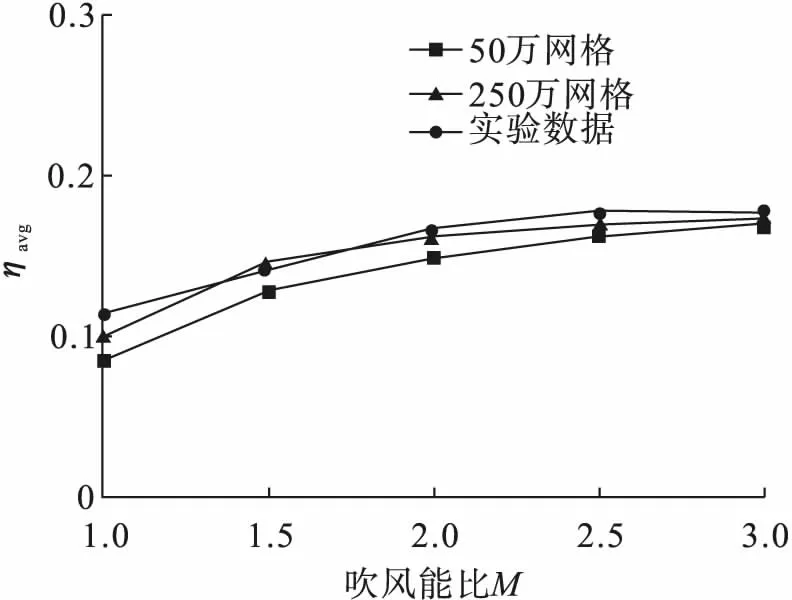
图4 计算结果与文献[14]实验数据对比

低可信度数据通过FLUENT对较为稀疏的网格进行控制方程求解获取，求解方法与高可信度计算方法相同。稀疏网格的质量约为密网格的1/5，二者拓扑结构以及冷却孔周围和壁端第一层网格的网格密度相同，只是改变气膜孔周围及下游区域的节点数，降低网格数量。如图5所示。

图5 2种不同质量网格图

高可信度数据通过FLUENT对高质量网格进行气相控制方程求解获取。湍流模型采用Realizablek-ε模型[7]，壁面函数采用增强壁面函数，压力和速度的耦合采用SIMPLE算法。密度、动量、湍流动能、湍流散耗率和能量的离散格式均采用二阶迎风格式；解的收敛标准是各项残差值均小于10-5，网格如图5b所示。

依据Fraas等[14]对扇形孔的研究，计算域边界条件设置如下：主流和次流进口均设置为速度入口，其中主流雷诺数为13×103，温度为510 K，湍流度为8.3，次流的速度根据吹风比决定，冷气温度为300 K。主流及冷气通道两侧采用周期边界条件，主流通道上侧面采用对称边界条件，其余面设置为无滑移绝热边界条件，如图6所示。计算工质为理想不可压缩气体。吹风比是影响气膜冷却性能的关键热力参数，定义为

(11)

式(11)中：ρc和Vc分别为冷气通道的入口密度和速度;ρ∞和V∞分别为主流通道的入口密度和速度。

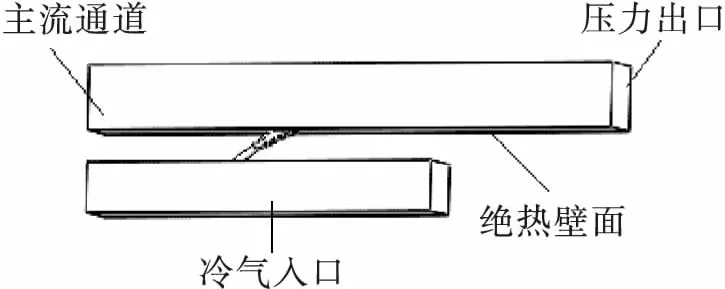
图6 计算域

表2为计算所得的数据样本，分别是36组低可信度样本、12组高可信度样本和测试代理模型精度的5组样本。

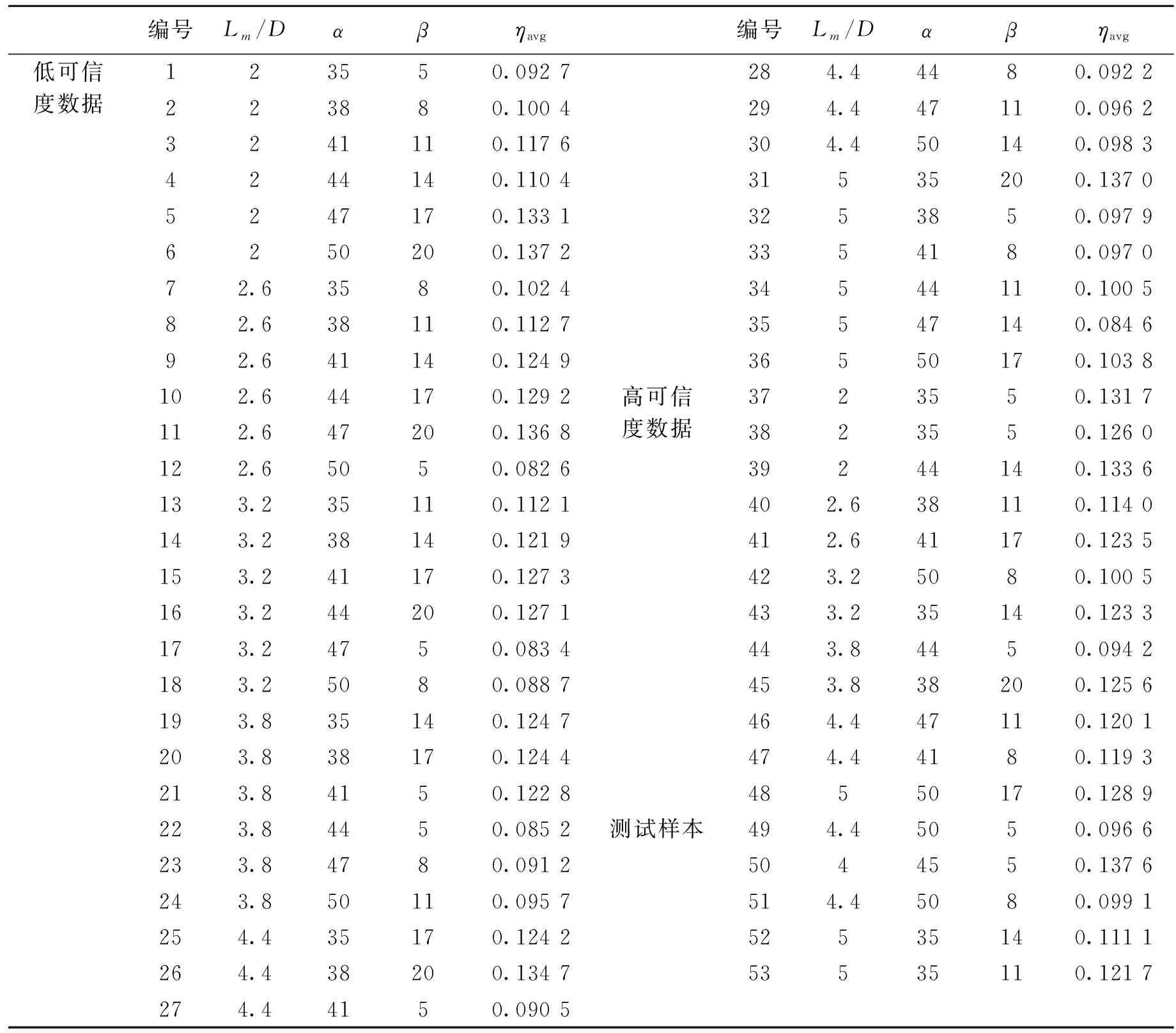
表2 训练样本和测试样本

为了验证 Co-Kriging 代理模型对平均气膜冷却效率拟合的精度，本文选取了5个样本点对其进行 CFD流场计算，并与Co-Kriging代理模型预测的值进行对比。结果如图7所示。Co-Kriging代理模型预测的值和CFD流场计算的相对均方根误差RSME值为 0.014 8，说明建立的代理模型对数据拟合的效果比较好。

图7 Co-Kriging预测值和CFD计算结果对比

遗传算法是一种全局性寻优算法，主要模拟了生物的繁殖、交叉和基因突变等情况。在每一次的迭代过程中都会保留一组最优解，并按照某种特定指标从下一代中选择较为优秀的个体，重复此过程，直到达到某种收敛指标。

算法迭代终止条件有两种，一种是规定最多遗传代数，达到指定目标后，不再继续迭代，自动停止计算；另一种方法是通过判断最终需要的结果是否满足条件且不再有进化的趋势，即可判断迭代终止，停止计算。如当群体中所有的个体的适应度已经满足小于某一个值，或者最优值满足收敛条件即可终止算法运行[15]，图8为遗传算法流程图。

以平均气膜冷却效率为优化目标，通过遗传算法对Co-Kriging代理模型进行全局寻优得到最优的扇形气膜冷却结构。遗传算法的设置如下，设置初始种群数量为50，适应度通过计算群体总适应值中个体的适应值所占比例来确定，交叉参数通过分散交叉函数确定，初始惩罚参数设置为10，惩罚因子为100，最大迭代步数为50。

图8 遗传算法流程图

将所要求解的优化问题描述如下

minF(Lm,α,β)=-ηavg

(12)

(13)

式(12)中:F(Lm,α,β)为适应度函数；ηavg通过Co-Kriging代理模型计算。

利用本文构建的Co-Kriging代理模型，以初始值Lm、α和β分别为3.8D、44°和5°为参考结构，表3为优化前后的扇形孔几何参数。图9为适应度函数随迭代步数的变化曲线，当迭代步数达到23步后，最优适应度函数值不再发生变化，适应度函数达到了最小值。

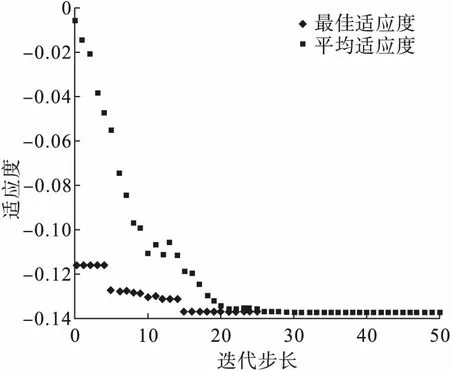
图9 适应度值随迭代步长的变化

表3 优化前后气膜冷却孔结构

2 结果与分析

图10为优化前后气膜绝热冷却效率分布云图。紧贴气膜孔的下游冷却效率比较高,沿主流方向冷却效率不断降低，气膜的展向覆盖不断收缩。此外，在紧邻气膜孔下游，2种不同尺寸的冷却孔在展向上的压力分布均呈现中央低、两侧高的特征，这是由于扇形气膜孔内冷却气流流动结构特征，这一压力的分布特征在优化后的扇形气膜冷却孔上表现得更为明显。在吹风比为1.5的工况下，通过优化，扇形孔下游区域从10D至15D冷却效率显著提高，冷气展向溢流能力得以强化。

图10 绝热表面冷却效率分布

图11为M=1.5的工况下，优化前后气膜孔出口y轴方向的速度分量。从图11中可以看出，冷却气体通过冷却孔与主流燃气混合，主流燃气对冷却气体有一定的压制，在混合后冷却气体速度明显降低。随着距离冷却孔越来越远，y方向上冷却气体的速度逐渐下降为0。优化后，扇形孔对壁面的覆盖面积增大，冷却孔有较大的出口面积，因此冷却气体可以均匀分布在冷却孔中心及两侧区域。在高吹风比下，优化前的冷却孔在距离孔中心位置较远的位置，对壁面的覆盖面积更少。这是因为高吹风比下，壁面下游更容易发生壁面分离。优化后，冷却孔中心处速度较大，因此冷却孔中心处的温度更低，流线更加密集。在距离冷却孔中心较远处，流线分散，从而对壁面进行有效覆盖。

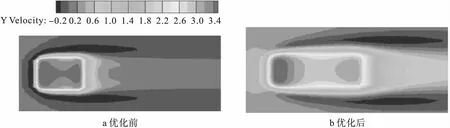
图11 气膜孔出口y轴方向的速度分量

图12a和图12c为优化前、后气膜孔下游X/D=1截面上温度分布及流线图，图12b和图12d为优化前、后气膜孔下游X/D=5截面上温度分布及流线图。其中在X/D=1的截面上，优化前的冷却孔出现了肾型涡对，肾型涡对的卷吸作用会导致涡核中心流体向上抬升，涡核两侧的流体向壁面压制，加剧冷气与热气的混掺，从而降低气膜冷却效率。优化后，扇形气膜孔下游的肾型涡对得到了很好地抑制，进场截面的流速比较均匀，更有利于增强气膜的展向覆盖能力。随着X/D的增加，反肾型涡对有所增强，大大提升了冷却性能。

图12 气膜孔下游温度与流场分布

图13为气膜孔内部速度等值线，冷气进入冷却孔后，在向心力和气膜孔轴向压力梯度作用下，气膜孔内部形成涡结构。由于肾型涡的存在，冷气不能很好地贴合壁面，对壁面的冷却效果较差。优化后的气膜冷却孔具有更大的前向扩展角和较小的直孔段孔长，有效地抑制肾型涡的形成，使混合后冷却气体能够更好地贴附在壁面，具有更好的贴壁性和展向扩展能力。

图13 孔内流场分布

3 结论

本文通过对扇形气膜冷却孔进行研究，可以得到以下结论：

(1)本文提出了一种基于两种可信度数据构建的Co-Kriging代理模型方法，通过对扇形气膜冷却孔的优化，Co-Kriging代理模型的误差在5%以内。通过使用遗传算法进行优化，优化后扇形气膜冷却孔相较于之前的参考结构冷却效率提高了45%。

(2)Co-Kriging代理模型可以有效利用低可信度数据来减少计算数据，缩短计算时间周期，具有较好的应用前景。

(3)最优的Lm、α和β为2.6D、41°和11°，与参考结构相比，具有更大的前向扩展角，能够更好地抑制肾型涡的形成，并且增大气膜冷却孔的展向覆盖面积。