一种新型双射流双喉道控制矢量喷管的数值模拟

王建明，刘晓东，夏瑄泽，张钲浩，王成军

(沈阳航空航天大学 a.航空发动机学院,b.辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136)

随着人们对战斗机性能要求的不断提高，仅提供操纵机翼翼面偏转以提升飞机机动性的方法已无法满足需求，因此推力矢量技术成为一项必不可少的航空推进技术。其中流体推力矢量喷管[1]以其结构简单和响应迅速的优势，逐渐代替传统的机械推力矢量喷管[2]，成为人们研究的新目标。流体推力矢量喷管是指喷管在非机械偏转状态下，通过注入二次流来达到控制主流方向进而实现气流的矢量偏转。根据工作原理的不同，流体推力矢量喷管有多种控制方式:激波矢量控制[3]、双喉道控制[4]、逆向流法[5]和同向流法[6]等。双喉道控制矢量喷管由于耗气量小、矢量效率高、推力系数大的特点，具有极大的发展前景。双喉道控制矢量喷管的工作原理是在原始的收扩喷管的后部增加一个收敛段形成第二喉道，在第一喉道处引入二次射流，在空腔内主流与下壁面分离形成回流区使主流发生偏转。

双喉道气动矢量喷管的概念最早是由NASA提出的[7]。随后的文献[8-9]对双喉道喷管做了更系统的参数化研究，文献[10-11]得出空腔内的流动分离是使主流偏转的主要原因，还提出扩张角大于10°后，推力矢量效率降低,研究中得出的最大矢量角为15°(8%次流流量)。文献[12-13]对落压比、次流流量、空腔长度、空腔扩张角、空腔收敛角等设计参数进行了系统的研究，设计参数为落压比3～4、次流流量3%、空腔扩张角为10°左右、收敛角为20°～30°、次流入射角度为150°时矢量推力性能较好。喷管空腔中的超声速区域的占比与矢量角和推力系数有密切关系[14-15]。文献[16-18]提出了一种在原有的双喉道喷管的后部增加一个扩张段，使主流流体在扩张段因附壁效应增大偏转角度，增强了矢量效果，并进一步对该喷管开展了内流特性试验研究，在研究中得出的最佳推力矢量角为24.1°、推力系数为92.9%，但此方法无法在维持较大矢量角的同时保持良好的推力系数。

为了进一步增强双喉道控制矢量喷管的矢量推力性能，本文提出了一种双射流双喉道矢量喷管，其原理是在原喷管的第二喉道处上壁面增加一个射流通道，进一步加大主流偏转的同时减低推力损失，既能保持较高推力矢量角，又能获得较大的推力系数。

1 研究对象及数值模拟方法

1.1 研究对象

本文所研究的双射流双喉道矢量喷管,是在双喉道矢量喷管的基础上进行改进的，原有的双喉道矢量喷管模型尺寸可参考文献[10]，如图1a所示。下游喉道高度hdt为29.21 mm，上游喉道高度为一倍的hdt。空腔长度为76.2 mm，空腔扩张角θ1为10°,空腔收敛角θ2为20°,第一喉道处的二次流入射角α1为30 °，在此基础上，在第二喉道处新增一个二次流射流如图1b所示，二次流入射角α2为120 °。

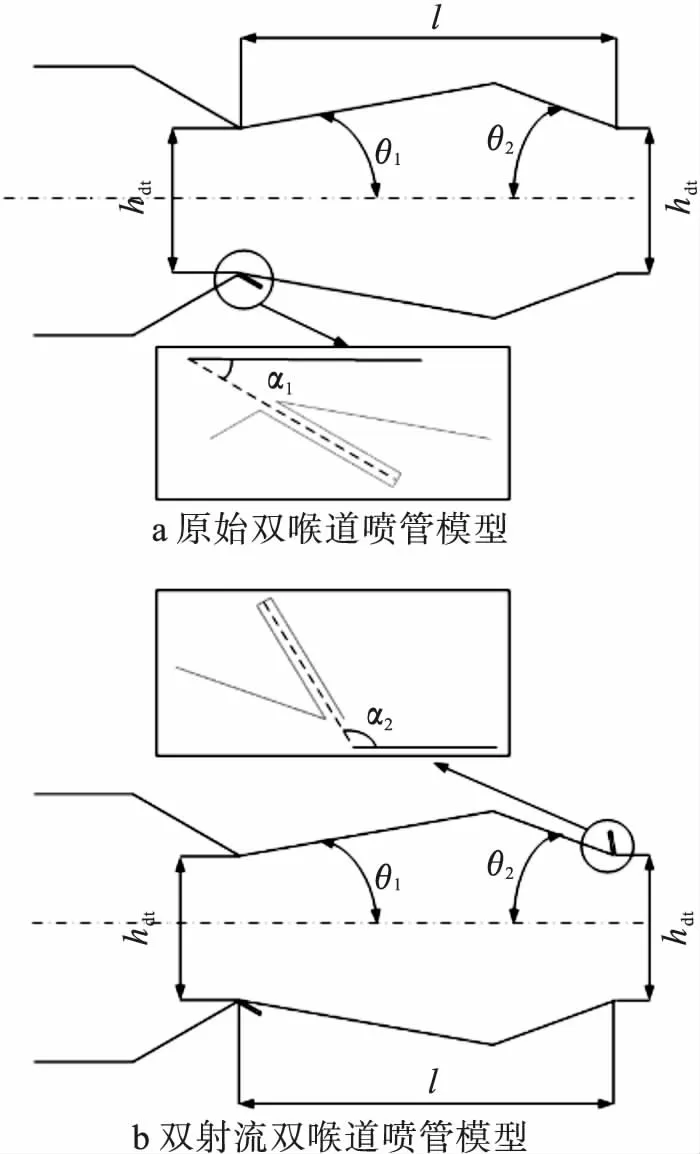
图1 双射流双喉道矢量喷管设计参数

1.2 控制方程

本文计算的可压缩粘性流体满足如下的控制方程：

连续性方程

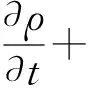
(1)

其中：ρ为流体密度；v为流体速度。

动量方程

(2)

其中：p为静压；Fi、gi分别为i方向上控制体所受到的重力体积力以及外部体积力；τij为应力张量。

能量方程

(3)

其中：E为流体微团总能；k是导热系数；T是温度；Sh为体积热源。

1.3 数值方法及计算设置

图2是划分的二维双射流双喉道矢量喷管的网格及其局部放大图，全部O型网格，近壁面第一层网格满足y+<1。

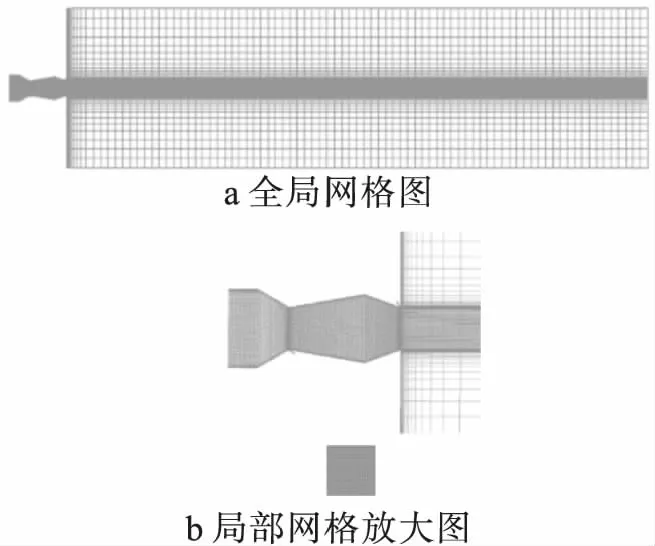
图2 网格与局部放大的网格图

采用FLUENT软件进行流场模拟。湍流模型为Realizablek-ε模型,离散方法采用了二阶迎风格式和隐式时间格式。参考文献[6]和[14]，喷管主流进口给定为压力入口；二次流进口均选用流量入口，其中位于第一喉道处的二次流流量恒定为w1=3.0%；位于第二喉道处的二次流流量由w2计算得出，喷管的主流进口与2个次流通道进口静温均为300 K。外流场边界给定为压力出口，其静压Pb=101 325 Pa,静温为300 K,其他边界均为无滑移绝热固壁边界。

1.4 喷管性能参数计算公式

本文对双射流双喉道矢量喷管的气动性能分析主要是通过推力矢量角和推力系数来表征。推力矢量角是喷管竖直方向力与水平方向力之比的反正切角。推力系数是喷管数值模拟计算推力与等熵流动推力的比值，反映了推力损失的大小。喷管性能相关参数如下

落压比NPR=P1/Pb

(4)

(5)

射流比w2=ws2/ws1

(6)

其中：P1为喷管主进口压力;Pb为环境背压;wp、ws1、ws2分别为主流流量、第一喉道处二次流流量、第二喉道处二次流流量。

参考文献[18]，推力矢量角是喷管水平推力与竖直推力的反正切函数值，可表示为

δ=arctan(Fy/Fx)

其中：Fx、Fy分别为水平推力与竖直推力，可表示为

水平推力Fx=Fp+∑(ρVex·ΔA)Vex

(7)

其中：压差力Fp=∑(Pe-Pb)·ΔA

(8)

竖直推力Fy=∑(ρVex·ΔA)Vey

(9)

其中：ρ为流体密度；Vex、Vey分别为气流出口水平方向与竖直方向速度；Pe为喷管出口压力；ΔA为喷管出口单元面积。

推力系数可表示为

Cf=Fr/Fs

(10)

其中：等熵推力

Fs=Fs1+Fs2+Fs3

(11)

喷管进口等熵推力

(12)

第一喉道处二次流等熵推力

(13)

第二喉道处二次流等熵推力

(14)

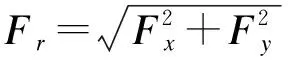
(15)

其中：V1、V2、V3，ΔA1、ΔA2、ΔA3，π1、π2、π3分别为主进口、第一喉道处二次流以及第二喉道处二次流所对应的进口速度、单位面积、落压比；γ取1.4；R取287.06 J/(kg·K)。

1.5 计算结果验证

图3为数值计算所得上壁面无量纲压力与实验对比，使用3万、6万、9万、12万共4组网格进行计算。图3中1和2圈出来的2处位置是不同网格模拟结果的主要差别之处，1区所对应的是喷管内λ激波所在的位置，2区所对应的是喷管上壁面的分离区位置，此两处位置的计算结果依赖于计算网格的数目。网格9万和12万的计算结果已经几乎没有差别，可以认为此时已经达到稳定；9万网格的计算结果和实验结果比较接近，因此选择9万网格进行计算的结果是准确的。

图3 数值计算所得上壁面无量纲压力与实验[10]的对比

2 结果与分析

2.1 双射流双喉道矢量喷管工作机理分析

图4给出了喷管改进前后的马赫数分布云图，NPR=4.0。次流流量比为3%时，原始双喉道喷管的推力矢量角为12.2°，推力系数为95.6%；在相同条件下，并且2个次流流量保持一致时，双射流双喉道喷管的推力矢量角达到16.5°，推力系数为96.7%。相较于原始双喉道喷管，改进后的双射流双喉道喷管是在第二喉道处增加一个二次流射流通道。一方面，此处的二次射流不仅可以有效地提高主流的竖直方向速度，增大主流流出喷管时竖直方向的力和推力矢量角，同时还可以有效地压缩主流，以气动的方式减小第二喉道的面积，在喷管进口压力一定的情况下，喉道面积减小，缓解了主流欠膨胀的情况，提高推力系数。此外，二次流的注入导致主流在流出喷管时上下面压力分布不对称，主流与外界大气接触后在上下面形成的膨胀波强度不一致，使后续波系相交发生变化，改变尾流流态。另一方面，主流流经喷管空腔下游时速度低于当地声速，在流经空腔上壁面收敛段时会受到下游射流的扰动，使主流与上壁面在靠近二次流通道处分离(如图4b 1区域放大图)，相当于增大了主流在空腔收敛段向下偏转的角度，进一步增大推力矢量角。此外，第二喉道处的二次射流也会对空腔上游的流态造成影响，主要体现在喷管空腔内主流处于亚声速状态的区域要占有更大的比值，空腔中游靠近回流区处的超声速区域变小会更有利于亚声速主流在空腔中下游发生偏转。

压力系数定义为

(16)

其中：Pin为矢量喷管入口压力；ρin和vin分别为喷管入口的流体的密度和速度。

图5a为双喉道喷管压力系数等值线，在空腔上游处存在明显的λ波，主流在回流区的作用下向上偏转，流经λ波压力逐级增大，速度降低至亚声速，可见λ波为较强激波；亚声速的主流再在空腔上壁面的收敛段的作用下向下偏转，最终流出喷管。如图5b所示，由于第二喉道处二次流的扰动，双射流双喉道喷管上游处未形成λ波，仅形成一道斜激波，主流在流经这道斜激波后速度为亚声速(如图4b 2区域放大图)。相较于原始双喉道矢量喷管在上游形成的λ波，改进后喷管的上游形成的斜激波可以有效地减小超声速区域面积，使主流在空腔中得到充分偏转，因此双射流双喉道喷管具有较大的矢量角。

图4 喷管改进前后的马赫数分布图

2.2 不同射流比对双射流双喉道矢量喷管性能的影响

为了进一步加深对双射流双喉道喷管的研究，本文以w2为变量(NPR、w1保持不变)，分析第二喉道处二次流流量对喷管推力矢量角与推力系数的影响。

图6为双射流双喉道喷管推力矢量角和推力系数随w2的变化曲线。从图6可以看出，推力矢量角先随着w2的增大而增加；推力系数则先随w2的增大而增加，随后又随着w2的增大整体呈现减少的态势。如表1所示，当w2=1.0，矢量角达到16.5°；当w2继续增大，矢量角趋于平稳，推力系数在w2=1.0时达到最大值，最大值为96.7%。

图7为NPR=4，w1=3%，w2为0.5、0.75、1、1.5时双射流双喉道喷管马赫数分布云图。从图7可以看出，w2较低时λ波仍存在，随着w2增大，λ波空间尺度逐渐减小，空腔中超声速区域占比降低，因此w2在此范围内增大会使推力矢量角增加。第二喉道处二次流流量增加也会加大射流对主流的压缩，使推力系数增加。当w2=1时，λ波完全转变成斜激波。当w2继续增大到1.5时，斜激波的位置基本不变，空腔上中游流场基本不变，推力矢量角趋于稳定,但是此时随着第二喉道处二次流流量的增大，二次射流与主流的掺混过程更加强烈，产生更大的推力损失。当w2大于1.5时，掺混损失其主要作用，导致推力系数降低。综上所述，在兼顾较大推力矢量角与推力系数的前提下，当w2维持在1.0～1.5时双射流双喉道喷管具有最好的矢量推力性能。

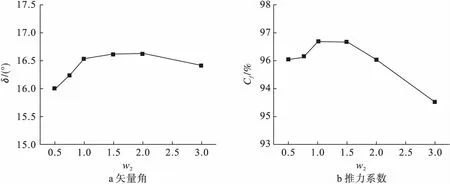
图6 矢量角、推力系数随w2的变化曲线

表1 不同射流比w2下的矢量角、推力系数

2.3 二次流入射角度α2对喷管流态和性能参数的影响研究

如图8所示，NPR=4.0,w1=3%，w2=1.0时推力矢量角和推力系数随二次流入射角α2的变化曲线，随着α2增大矢量角逐渐减小；推力系数则随着α2先增大后减小。如表2所示，矢量角在α2=100°时达到最大值，为17.2°；推力系数在α2=120°时达到最大值，为96.7%。

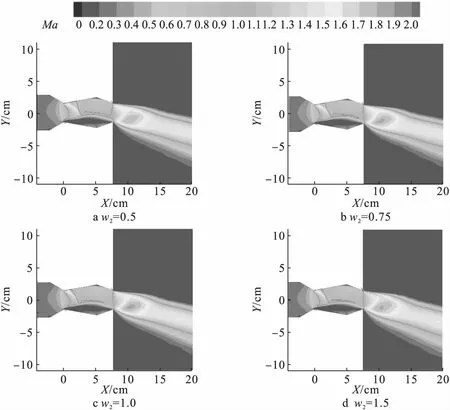
图7 不同射流比时的马赫数分布图

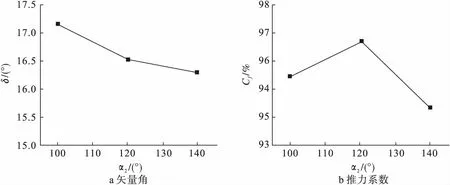
图8 矢量角、推力系数随入射角α2的变化曲线

表2 不同入射角下的矢量角、推力系数

图9为入射角α2分别为100°、120°、140°时3种喷管马赫数分布云图，α2=100°时空腔上游只存在斜激波，第一喉道以及回流区附近超声速区域面积最小；随着α2增大，超声速区域面积增大，α2=140°时，第一喉道以及回流区附近超声速区域面积最大，在空腔上游处存在明显的λ波，尾流呈明显膨胀波交叉流态，二次射流抑制尾流膨胀的能力较弱，因此随着α2的增大喷管的矢量角减小。但是当α2=100°时，由于射流角度过小导致射流对主流的压缩程度下降，推力损失增大，推力系数较120°时有所减小。综上所述，考虑矢量角与推力系数两方面因素，二次流入射角α2=120°时矢量推力性能最佳。

图9 不同入射角α2时的马赫数分布图

3 结论

在双喉道矢量喷管的基础上提出了一种双射流双喉道矢量喷管的概念，并对该喷管的二维模型的静态特性进行了初步的参数化数值模拟研究，研究中始终使落压比NPR=4.0保持不变，研究结果表明：

(1)相较于原始双喉道喷管，改进后的双射流双喉道喷管可以有效地抑制λ波的产生，增加主流在空腔中的偏转角度，提高推力矢量角的同时在第二喉道处压缩主流，改变尾流流态，降低推力损失，提高推力系数，研究中得到的最大矢量角为16.5°，推力系数得到96.7%。由此可以证明双射流双喉道矢量喷管有很好的推力矢量性能。

(2)次流流量比w2会影响喷管空腔的整体流态，随着w2的增大推力矢量角逐步增大，当w2高于1.0时，流场基本不变，推力矢量角不再变化；由于射流对主流的压缩作用的增强推力系数一开始逐渐增大，但是w2大于1.5时射流的掺混损失会起主要作用，导致推力系数变小。入射角α2的增加会提高推力矢量角，但是α2过大或过小都会减弱二次流对主流的压缩，降低推力系数。综合考虑w2维持在1.0～1.5，入射角α2为120°时具有最好的推力性能。