图像去噪与增强中的改进自适应分数阶中值滤波*
张雪峰, 刘 日, 任建旭, 桂清龙
(①东北大学理学院;②东北大学机械工程与自动化学院,110819,辽宁省沈阳市)
0 引 言
数字图像在采集、传输或处理等过程中不可避免地会受到噪声影响. 噪声不仅使图像的视觉效果变差,还会影响后续图像的识别和分割等工作. 因此图像去噪算法的研究是数字图像处理中的重要部分[1].
图像噪声有很多种,如脉冲噪声、高斯噪声、泊松噪声等,其中脉冲噪声也称椒盐噪声,是一种常见的图像噪声,其是一种随机出现黑点或白点的噪声,对于一幅经典的8位灰度图,灰度值为0意味着黑点,灰度值为255意味着白点. 处理椒盐噪声的经典方法是利用中值滤波[2,3]处理,但传统中值滤波算法不区分噪声点和信号点,而对所有像素点统一处理,故去噪的同时也可能滤去了信号点,这使得图像边缘细节大幅丢失,而且该方法在噪声密度大于50%时近乎失效. 因此,很多学者提出了改进措施,如中值滤波与小波变换结合[4],加权自适应中值滤波[5]等,这些算法在噪声密度较低时均有很好的效果,但在实际应用中都存在一定的局限性,如在噪声密度较高时去除噪声不完全,去噪后的图像会变模糊. 而在去除噪声后,一般图像的边缘细节都会有一些丢失,导致图像的视觉效果变差,这就需要对去噪后的图像进行增强.
图像增强是为了使图像边缘细节更加清晰,视觉效果更好,同时更适于后续处理图像的工作. 增强图像有梯度场增强算法[6]或使用微分算子来处理图像,用整数阶微分算子处理图像,但效果并不理想,出现增强不明显,破坏平滑区域等问题. 近年来,分数阶微分算子逐渐被用于处理图像[7-9],文献[10]提出了一种分数阶微分掩模,应用于图像的多尺度纹理增强,文献[11]提出了一种自适应分数阶全变差图像恢复的方法,文献[12]提出了基于4个分数阶偏微分方程的多尺度去噪模型.
目前,用分数阶微分算子处理图像已经成为热点问题,众多文献已经应用该方法且取得了一定效果. 文献[13]利用Grümwald-Letnikov定义的分数阶设计了一种分数阶微分掩模,将分数阶引入图像处理中. 其设计的算法对图像边缘部分进行增强,但图像平滑区变得模糊,导致最终视觉效果并不理想. 之后文献[14]引入一维Savitzky-Golay滤波器,将其从整数阶推广到分数阶,并从一维推广到二维,进而提出了基于二维Savitzky-Golay滤波器的图像增强算法,得到的图像平滑区几乎没有改变,边缘细节也得到了增强,但增强效果并不突出. 在图像处理领域引进分数阶的方法在近几年的热度依然不减,文献[15]将去噪与增强结合起来,去除噪声且增强了图像,其算法解决了传统方法会使图像模糊化的同时增强了图像边缘,但其算法处理结果的对比度并不高. 文献[16]提出了一种分数阶梯度能量算子,并将其应用于图像融合中,相比于整数阶梯度能量清晰度算子,该融合方法有效避免了融合图像中的伪影和块状效应,更充分地保留了源图像信息.
为了解决噪声消除不完全且去噪后图像边缘信息不突出的问题,本文提出一种改进的新算法. 设计一个检测椒盐噪声的开关,进而利用中值滤波设计一种开关滤波去除噪声,消除噪声的同时保留了正常像素点. 之后为了使图像的视觉效果更好,即边缘细节更突出且不会模糊其他区域,本文根据图像自身特性设计了一种自适应算法,利用分数阶滤波器对每一个像素点用不同阶次的分数阶滤波器处理. 由于分数阶微分算子具有弱导数性,故其增强效果明显优于整数阶. 本文提出改进的自适应分数阶中值滤波在去除椒盐噪声的同时对图像进行增强,相较于文献[13-15]在图像边缘细节增强更明显,纹理细节更突出,较好地克服了经典中值滤波去噪及传统分数阶滤波增强会使图像模糊化及增强效果不明显的缺点.
1 预备知识
1.1 二维中值滤波
中值滤波是基于排序统计理论的一种能有效抑制噪声的非线性信号处理技术,在图像增强和复原中被广泛应用. 中值滤波器的响应基于由滤波器包围的图像区域中像素灰度值的中值. 利用中值滤波处理图像,是指对图像中的任意一点(x,y),以该点为中心设计中值滤波窗口,在该窗口内将像素点的灰度值按从小到大进行排序,取排列中值作为(x,y)点的滤波结果,即
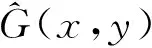
传统中值滤波对低密度椒盐噪声去除效果较好,但在噪声密度较高时效果并不理想,而经过多次中值滤波处理,噪声虽然能够消除,但是重复使用中值滤波处理可能会使图像模糊化.
1.2 分数阶定义
分数阶定义表达式主要有3种形式:Capotu定义、Riemann-Liouville定义与Grümwald-Letnikov定义[17]. 函数f(t)的Capotu定义为
其中n=[α]+1,n-1<α≤n,t>a,Γ(·)为伽玛函数. 函数f(t)的Riemann-Liouville定义为
以上2种定义均使用了Cauchy积分公式,其复杂度较高,不利于进行大规模的数据计算. 而G-L定义(Grümwald-Letnikov,简称G-L)可以转化为卷积的形式,因此相较于其他两种定义在图像处理中有更好的效果,函数f(s)的G-L定义为
式中h为步长,Γ(·)为伽玛函数.
1.3 分数阶微分对信号的增强作用
已知对任意平方可积能量信号f(t)∈L2(),由信号处理基本理论可得到其Fourier变换为
设信号f(t)的n阶导数是f(n)(t),n∈,由Fourier变换性质可得
若信号f(t)的阶数为v的分数阶导数为f(v)(t),v∈+,由分数阶Fourier变化可得[18]
式中
由以上可得当分数阶阶次v为0.1,0.2,0.3,0.5,0.6,0.8时的幅频特性曲线,如图1所示.
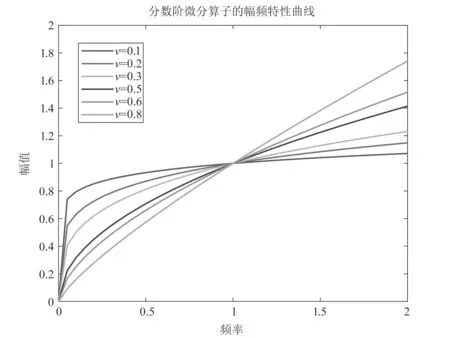
图1 分数阶微分算子幅频特性曲线
由图1可知,分数阶阶次在0.5以下时,相对应的微分算子对于信号幅值有一定提升,但相对于0.5以上的分数阶阶次提升幅度较小. 因此,分数阶的阶次对图像具有不同的作用,可根据图像局部信息与特征来改变微分阶次,从而实现对图像不同区域的有效增强.
2 图像去噪与增强算法
2.1 椒盐噪声检测与去噪算法
在图像去噪过程中,正确判断噪声点是去噪的关键. 本文根据椒盐噪声的特性,即噪声总是将像素点的灰度值数字化为0或255,根据噪声这一特点便可以很容易检测出可疑噪声点. 下面为本文噪声检测的步骤.
第1步:设一幅图像大小为x×y,G(xi,yi)为图像第i个点的灰度值. 若某点的灰度值为0或255,标记该点为可疑噪声点;若该点的灰度值为其他值,则代表其为正常点. 标记方式为
第2步:对于上一步的可疑噪声点,因原图像本身可能存在灰度值为0或255的点,所以为了降低误检率,对这些点进一步检测. 设图像中某一可疑噪声点G(x,y),以该点为中心,建立一个3×3的检测窗口,计算窗口内灰度值为0~255之间的个数A1,灰度值为255的个数A2,灰度值为0的个数A3.
(1)若A1=0,即窗口内均为可疑噪声点.
①若A2=9或A3=9,说明该窗口内均为黑色像素点或白色像素点. 在该情况下,认为该区域即原图中本有的白色或黑色区域.
②若A2>A3,即该窗口内白色点比黑色点多,此时可以将该点处灰度值按255输出.
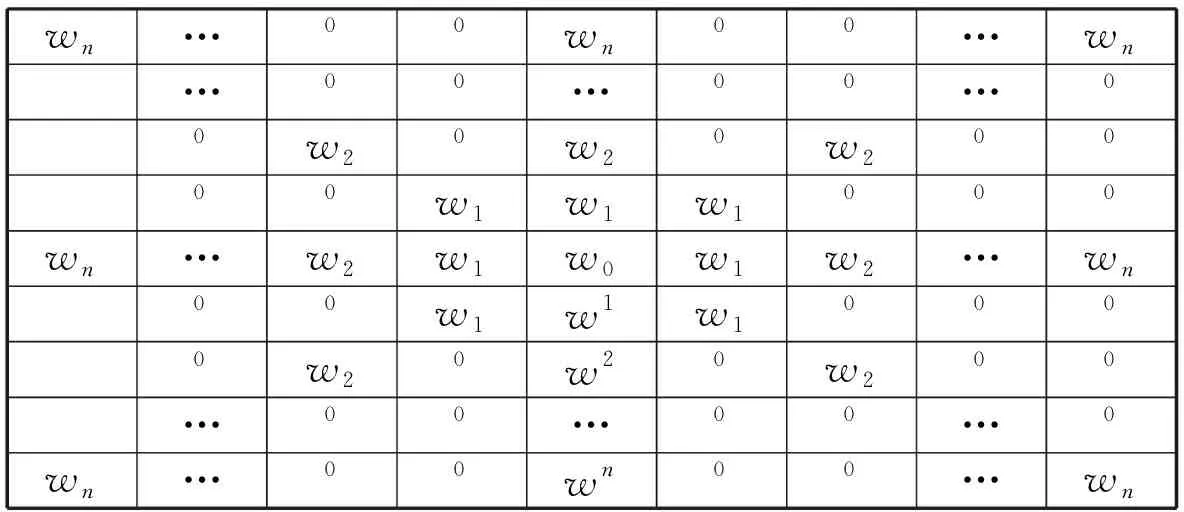
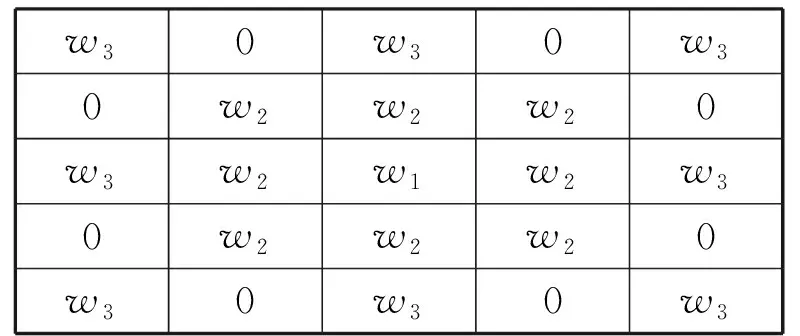
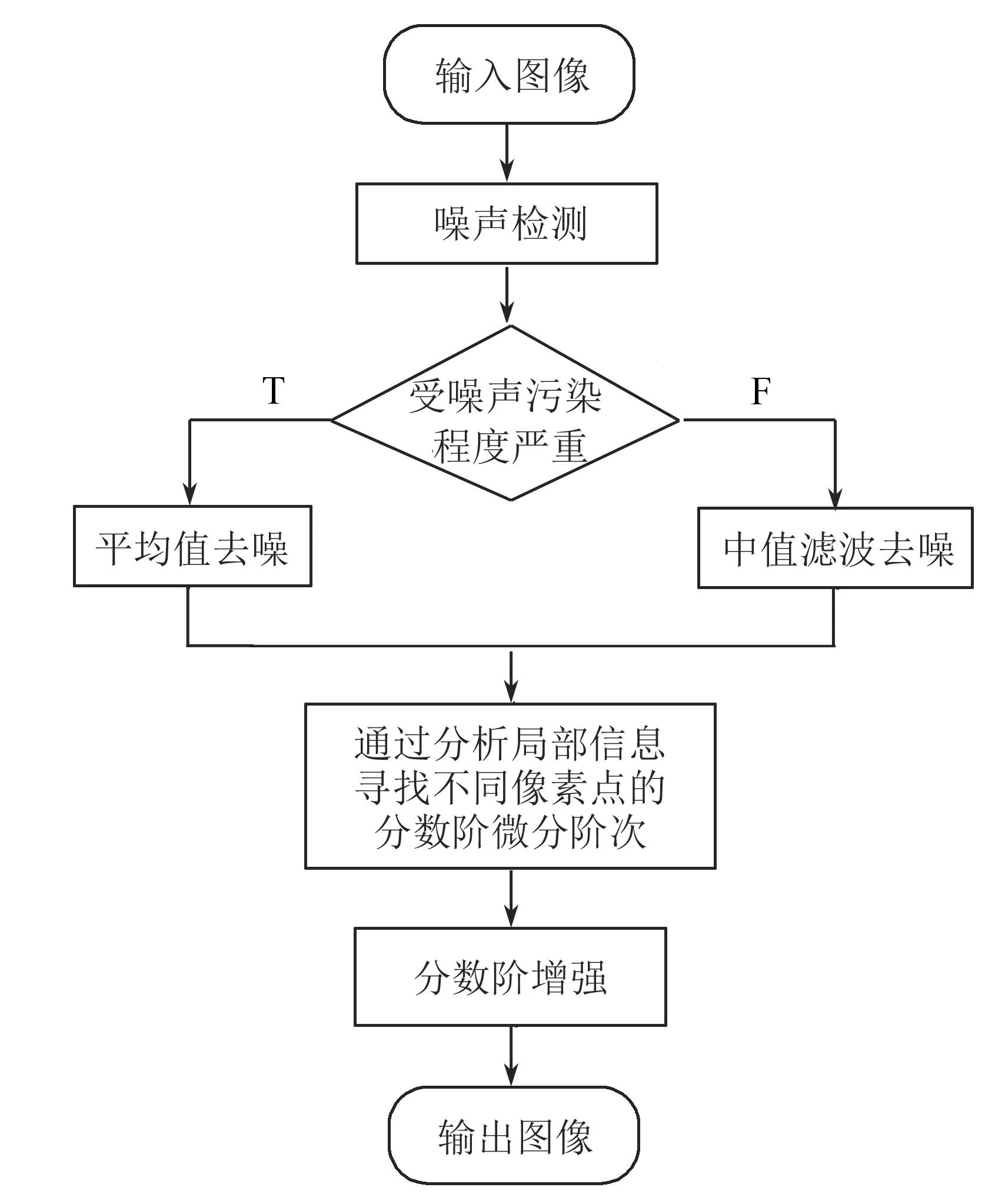
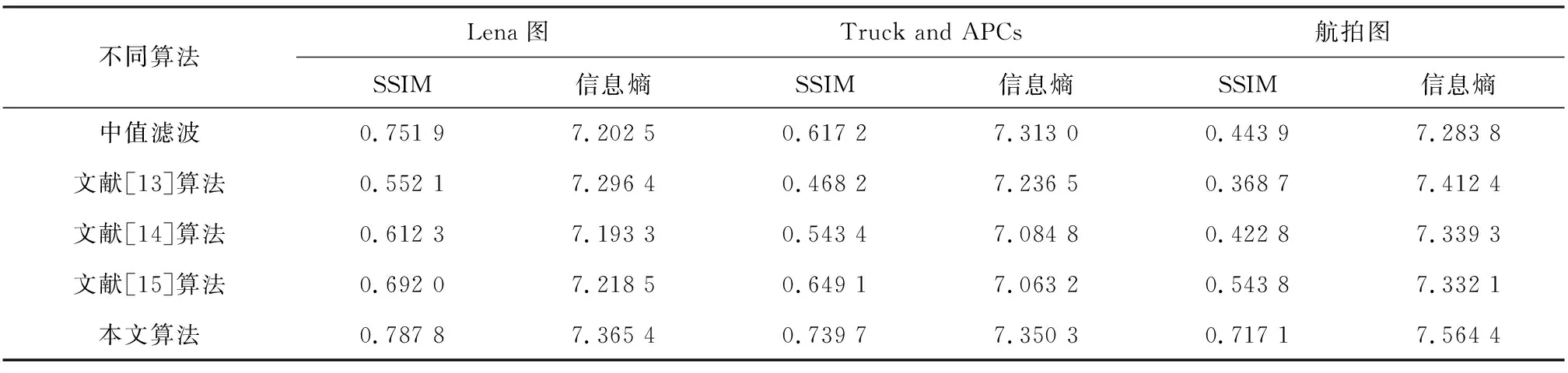
③若A2 (2)若A1≠0,则继续考察该3×3窗口内的像素值,如图2所示,判断该窗口内像素受污染程度. 根据受污染程度,用不同的去噪方法来达到较好的效果. 用该窗口内除中心像素点之外的其余像素点灰度值与中心像素点灰度值作差的绝对值小于阈值的个数来判断,计算方式为 Ha=|G(i+m,j+n)-G(i,j)|≤10, 若β<1,说明该窗口受噪声污染严重,利用该窗口内非0、非255的其余灰度值的平均值来代替该点的灰度值. 若β>1,说明该窗口受噪声污染并不严重,此时利用中值滤波进行去噪. G(i-1,j-1)G(i-1,j)G(i-1,j+1)G(i,j-1)G(i,j)G(i,j+1)G(i+1,j-1)G(i+1,j)G(i+1,j+1) 在图像增强过程中,分数阶微分的阶次不仅与梯度幅值平均值、梯度幅值的最大值、梯度幅值的最小值有关,还受到图像局部信息的影响. 本文为了更好地增强图像边缘细节,根据图像的局部信息设计出一种自适应算法,可以根据图像的局部信息来计算出适当的分数阶. 图3 自适应算法流程图 由以上3个反应图像局部信息的定义可知,局部信息参数M,S,C的值越大,表明该区域为目标增强区域的概率越大,分数阶的阶次也应更大;M,S,C的值越小,该区域为目标增强区域的概率越小,分数阶的阶次也应越小.由此可知,分数阶阶次的大小与3个图像局部参数值大小成正相关. 本文将上述3个局部重要信息的参量进行加权求和,故设P=λ(k1·M+k2·S+k3·C),其中k1,k2,k3为加权系数,三者和为1,λ为调节参数. 又由于e指数在实数域上为增函数,增强幅度随变量的增加而增加,与本文算法想要达到的目的相符合,故能得到分数阶微分自适应算法v=eP-Q,式中Q为调节参数. 经过多次实验,且在本算法中,图像的粗糙度较其他两个特征参数更能反应图像局部特征,故取λ=1,k1=0.3,k2=0.1,k3=0.6,Q=1.8. 分数阶微分滤波不仅对图像高频信号有加强作用,还能非线性地保留一些低频信息. 因此在图像处理中,利用分数阶微分增强边缘纹理细节,而且在一定程度上保留图像平滑区信息. 为了使图像分别完成在8个中心对称方向上的分数阶微分运算,达到增强算法的抗旋转性能,把以上两式推广到其他6个方向(0°,45°,90°,135°,225°,315°),得到一个基于8个方向的分数阶微分滤波器[13](图4). wn…00wn00…wn…00…00…00w20w20w20000w1w1w1000wn…w2w1w0w1w2…wn00w1w1w10000w20w20w200…00…00…0wn…00wn00…wn 本文在图像增强方面选择经典的8个方向滤波窗口大小为5×5的分数阶微分滤波器. 如下页图5所示. 将图5中的每项元素除以8-12v+4v2,再与图像做卷积,就能得到v阶次的分数阶微分处理的图像. 传统的增强方法是只使用同一分数阶微分阶次来处理图像,会出现边缘过度增强而平滑区变模糊的状况. 由于本文的增强算法是自适应的,这就使得得到的增强图像边缘部分更加突出的同时,较好的保留了平滑区的图像信息,即没有对原图非纹理部分进行破坏. 这就使得增强后的整幅图像更适于识别,同样适于后续的分割等工作. w30w30w30w2w2w20w3w2w1w2w30w2w2w20w30w30w3 利用中值滤波设计的开关滤波器以及自适应分数阶增强算法对图像进行处理的算法流程图如图6. 图6 算法流程图 在MatlabR2017a平台上实现本文的编程算法,并选取了“Lena”等3种灰度图像(图7)进行实验,改变椒盐噪声的密度得到不同的实验结果. (a)Lena原图 (b)Truck and APCs原图 (c)航拍图原图 图8是“Lena”图的实验结果. 首先在“Lena”图中加入密度为20%的椒盐噪声,分别用中值滤波、文献[13-15]算法以及本文算法处理. 本文算法使平滑区信息保留完好,而且增强了图像的边缘,相较于原图更加清晰. 再从视觉的角度出发,可以清楚地看到本文算法相较于其他算法在头发、帽子等边缘细节有更好的处理效果. 这表明了本文算法在去除椒盐噪声的同时对图像进行了增强,证明了本文算法的有效性. (a)20%椒盐噪声 (b)中值滤波 (c)文献[13]算法 (d)文献[14]算法 (e)文献[15]算法 (f)本文算法 “Truck and APCs”实验效果如图9所示. 先对“Truck and APCs”图像加入密度为30%的椒盐噪声. 本文算法基本将噪声完全去除且对边缘有明显增强效果,视觉效果更好. 而使用中值滤波处理后,噪声仍有残留,严重影响了图像的观感,其他算法在处理图像纹理细节时,增强效果不明显. 这表明本文算法相较于其他算法有提高. (a)30%椒盐噪声 (b)中值滤波 (c)文献[13]算法 (d)文献[14]算法 (e)文献[15]算法 (f)本文算法 图10展示了一幅航拍图. 对其添加40%的椒盐噪声,实验结果如图. 由图可见,本文算法有效地去除了噪声,处理后的图像边缘轮廓相较于其他算法比较突出,平滑区也比较清晰,整张图片很有层次感. 这再次表明本文改进的自适应分数阶中值滤波在图像去噪与增强方面的优越性. (a)40%椒盐噪声 (b)中值滤波 (c)文献[13]算法 (d)文献[14]算法 (e)文献[15]算法 (f)本文算法 图11展示的是一幅实际图像分别用不同文献算法与本文算法处理的结果. 由图11可见,本文算法的处理结果相较于其他算法小船的轮廓更为清晰,树叶棱角分明,云层的边缘更加明显,但云层的主体部分相较于原图改变不大,这很直观地说明了本文算法对图像纹理区的加强相较于其他算法更为有效,且更好地保护了图像平滑区的信息. 文献[6]算法(梯度场增强算法)的处理结果的亮度显然高于其他算法的处理结果,这是因为梯度场增强算法会显著提高图像的对比度,但这种算法对于图像纹理区的加强相较于本文算法不够明显. (a)实际图像 (b)文献[13]算法 (c)文献[14]算法 (d)文献[15]算法 (e)文献[6]算法 (f)本文算法 图12也是对于一幅实际图像用不同算法的处理结果. 可以看到原图飞机上的字母和图案不够清晰,同时对边缘细节增强不明显,而本文算法的处理结果字母最为清晰. 本文对山脉的处理结果也显然优于其他算法. 本文对云层的轮廓部分增强明显,且对云层主体部分基本保持与原图一致. 这再一次说明了本文算法对于纹理区域的增强和平滑区的保持做到了很好的平衡. (a)实际图像 (b)文献[13]算法 (c)文献[14]算法 (d)文献[15]算法 (e)文献[6]算法 (f)本文算法 首先,通过对图像直接观察,进行主观评价. 由图7可以看出,在添加椒盐噪声比例较小时中值滤波处理结果获得了比较好的效果,但是出现了局部模糊的问题,文献[13-15]算法处理结果也比较满意,但相较于本文算法仍有不足. 可以看到本文算法在Lena图的帽子、头发和眼睛等边缘细节、纹理部分的加强效果都很好. 由图9和10可以看出,在添加椒盐噪声比例提高时中值滤波处理结果较差,处理后的图像仍有较多的噪声点. 文献[13-15]虽对图像进行增强,但增强效果并不明显且部分平滑区会出现模糊的情况. 在噪声密度较高时,本文算法仍保持较好的消除噪声功效,同时对边缘纹理部分有明显增强,视觉上也有良好的提升. 如图13所示,分别将本文算法的效果图与原图作差分,以检测本文算法对图像边缘及纹理细节的增强效果. 可以看到图13中各图的边缘及纹理细节部分清晰可见,且没有多余噪声点,从而说明本文算法在去除椒盐噪声及增强边缘和纹理细节部分的有效性. 图13 本文算法与原图差分 利用中值滤波设计的开关滤波处理过后,图像受噪声影响绝大部分消除,3幅图像处理过后基本没有噪声点;对图像进行分数阶微分处理后,图像的边缘细节得到增强,Lena图中在帽檐、头发、脸部轮廓以及眼睛处纹理更加清晰了. APCs图中每个小车的车体更加清楚,且部分杂草的边缘看起来也明显了许多. 对于航拍图,边缘保持较明显的地方在于左下角较长的两条交错街道,以及右上角有一个缺口的地方. 这些细节都能体现本算法在增强边缘的有效性. 本文采用SSIM[22](Structural Similarity Index)来衡量两幅图像的相似度,可以通过计算两幅图像结构信息的相似性来检测图像质量的好坏,并且在视觉特征上比传统的MSE、PSNR方式更符合人眼视觉感知. SSIM的取值范围为[0,1],值越大,表示图像失真越小,即图像视觉效果越好. 图像信息熵表示一个随机性变量. 图像的平滑区域信息熵较小,纹理丰富区域信息熵较大. 由表1可以看出,相较于其他算法,本文算法的SSIM值均比较大,图像信息熵比较高,这表明本文算法在尽可能保持与原图一致的情况下加强了图像的边缘和纹理细节部分. 而文献[13]和文献[14]算法处理图的SSIM值比较小,这是因为同一分数阶阶次处理整幅图像会出现过度增强的情况. 文献[15]提出的去噪增强算法也有较好效果,但相较于本文算法仍有不足. 从图8~图10可以看出本文算法对于图像边缘与纹理细节部分的增强效果最优. 从图11和图12的处理结果可以看出,本文在处理实际图像时,不论是对图像纹理区的增强还是对图像平滑区的保持都要优于其他算法;从表2的数据也可以看出,本文算法的SSIM值和信息熵值比其他算法的都大,这也从侧面反映了本文算法的有效性. 表1 不同算法下的SSIM和信息熵值 表2 不同算法下对实际图像处理后的的SSIM和信息熵值 基于中值滤波器和自适应分数阶滤波器,根据椒盐噪声的特点,提出了一种去除椒盐噪声并增强图像的方法. 本文方法主要利用了新的噪声检测机制对图像进行去噪,在有效去除噪声的基础上利用自适应分数阶增强算法对图像进行增强. 本文提出的方法克服了传统中值滤波器的缺点,并在保持图像平滑区基本不变的情况下增强了图像边缘与纹理细节部分. 最后通过实验表明本文算法在去除椒盐噪声和增强图像细节方面有很好的效果. 然而,本文提出的方法在实际应用中仍然有不足之处. 在今后的研究工作还需着重解决以下问题:如何更加准确地确定图像局部信息与分数阶微分阶次的关系,从而构造更为精确的自适应函数;如何通过优化算法,进一步缩短处理图像所需时间.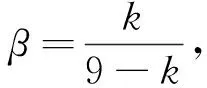

2.2 自适应算法
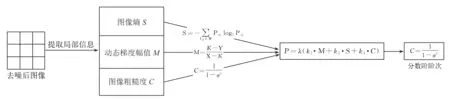
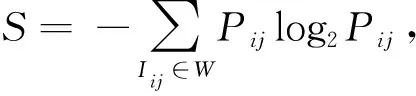
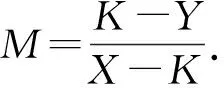

2.3 图像增强算法
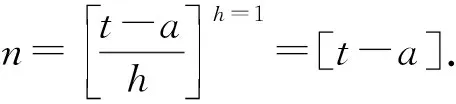

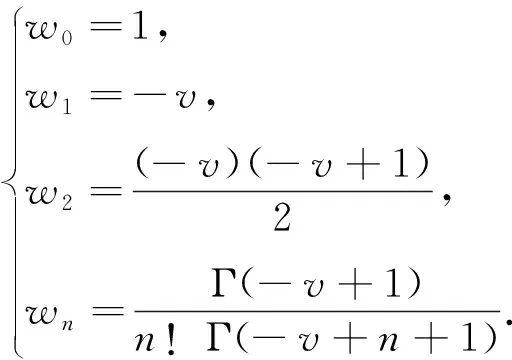
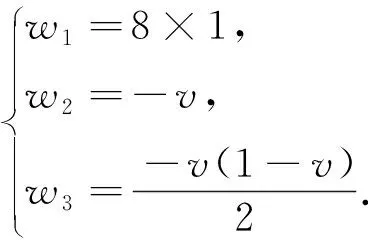
3 实验结果及分析
3.1 实验结果






3.2 结果分析


4 结 论

