工件可拒绝与机器具有退化维护活动的无关机排序问题*
高 洁, 隋玉康, 邹 娟, 孙安宁
(曲阜师范大学数学科学学院,273165,山东省曲阜市)
0 引 言
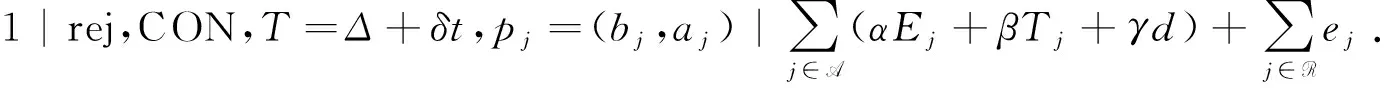
本文的结构如下:第1节对研究的问题进行了描述;第2节给出相关的引理;第3节给出问题的多项式时间算法;第4节对本文的研究进行了总结.
1 问题描述
本文讨论的问题描述如下:给定工件集N={1,2,…,n}和m台无关机M={1,2,…,m}.工件j或者被接受并被安排到某台机器上进行不中断的加工,或者被拒绝并支付拒绝费用ej. 设A与R分别表示接受工件集和拒绝工件集. 为方便起见,安排在机器i上加工的工件集记为Ai,ni表示在机器i上加工的工件数量,i=1,2,…,m. 显然,Ai可以为空集,|Ai|=ni,Ai∩Aj=∅(i≠j)且A=A1∪A2∪…∪Am.
为了提高机器的生产效率,我们可以对每台机器执行至多一次的退化维护活动,机器在维护时段不能加工任何工件. 根据文献 [2],假设机器i上退化维护活动 (MAi) 的维护时间Ti是其开始时刻的线性非减函数,表示为Ti=ti+δit,其中ti>0是基本维护时间,δi>0为维护系数,t为退化维护活动的开始时刻. 为方便起见,如果机器i上MAi在第ki个位置上的工件开始加工之前恰好执行完成,那么称机器i上MAi的位置为ki. 特别地,ki=1表示机器i在 0 时刻执行MAi,ki=ni+1表示机器i不执行MAi. 定义bij与aij分别表示工件j在机器i的退化维护活动之前与之后的加工时间,且0 对于一个给定的排序,令Cij表示工件j在机器i上的完工时间,令D=(d1,d2,…,dm)表示公共交货期向量,其中di表示机器i上工件集的公共交货期.Eij=max{0,di-Cij}和Tij=max{0,Cij-di}分别表示工件j在机器i上的提前时间和延误时间. 我们的目标是寻找退化维护活动的位置、接受工件的排序以及每台机器上接受工件的公共交货期,使得目标函数 最小,其中α>0与β>0分别表示单位时间的提前惩罚和延误惩罚. 依据传统的三参数表示法[8],将本文研究的问题表示为 其中,rej表示工件可拒绝,Ti=ti+δit表示机器i上维护活动的维护时长,pij=(bij,aij)分别表示基础加工时间和缩短加工时间. 为了解决问题(P),我们首先给出如下几个重要的结论. 引理2.3[2]在单机环境下,在最优排序中,维护活动或者在0时刻执行,或者在最优公共交货期d之后执行. 由引理 2.2 与引理 2.3,可以得到无关机环境下的两个结论. 为了叙述的方便,令i[j]表示机器i上的第j个位置. 引理3.2在最优排序中,机器i(1≤i≤m)上的退化维护活动或者在0时刻执行,或者在di时刻之后执行. 为了分析出本文研究问题的最优排序,首先,根据维护活动的不同位置,分别计算机器i上的总提前和延误惩罚: 情形1 维护活动MAi在 0 时刻开始执行,即ki=1. 情形2 维护活动MAi在di时刻之后执行,即hi+1≤ki≤ni. 情形3 不执行维护活动MAi,即ki=ni+1. 可以看到,对于情形2,若取ki=ni+1,则可以得到与情形3相同的表达式,故将这两类归为一类. 因此,讨论任意机器i上退化维护活动的位置,只需要考虑ki=1与hi+1≤ki≤ni+1这两种情形. 证明对于这个问题,可以将其转化为指派问题(AP)求解. 对于任一给定的工件分配向量P(n,m+1)=(n1,…,nm,nm+1)与维护活动的位置向量Q(n,m)=(k1,…,km). 由以上分析,可以将维护活动的位置向量分为以下3类:(1)Q(n,m)=(1,…,1),即每台机器均在0时刻执行退化维护活动;(2)Q(n,m)=(k1,…,km),其中hi+1≤ki≤ni+1,i=1,2,…,m,即每台机器均在di时刻之后执行退化维护活动;(3)Q(n,m)=(1,…,1,kl+1,…,km),其中hi+1≤ki≤ni+1,i=l+1,l+2,…,m,即在机器i=1,…,l上,机器在 0 时刻执行退化维护活动,在机器i=l+1,…,m上,机器在di时刻之后执行退化维护活动. 令变量xijs=1表示工件j被安排到机器i的位置s,否则xijs=0;令wijs表示工件j被安排到机器i的位置s时的权重. 我们分别对Q(n,m)的3个分类进行分析. 我们将对应于工件分配向量P(n,m+1)=(n1,…,nm,nm+1)与维护活动的位置向量Q(n,m)=(k1,…,km)的指派问题记为AP(n1,…,nm,nm+1,k1,…,km),并将对应的目标函数值记为Z(n1,…,nm,nm+1,k1,…,km),简记为Z. (1)若Q(n,m)=(1,…,1),可以得到 因此,对于给定的工件分配向量P(n,m+1)=(n1,…,nm,nm+1)与维护活动的位置向量Q(n,m)=(1,…,1),我们将问题重新描述为下面的指派问题AP(n1,…,nm,nm+1,1,…,1): 其中 (2)若Q(n,m)=(k1,…,km),其中hi+1≤ki≤ni+1,i=1,2,…,m,可以得到 因此,对于给定的工件分配向量P(n,m+1)=(n1,…,nm,nm+1)与维护活动的位置向量Q(n,m)=(k1,…,km),其中hi+1≤ki≤ni+1,i=1,2,…,m,将问题重新描述为下面的指派问题AP(n1,…,nm,nm+1,k1,…,km): 其中 (3)若Q(n,m)=(1,…,1,kl+1,…,km),其中hi+1≤ki≤ni+1,i=l+1,l+2,…,m,可以得到 因此,对于给定的工件分配向量P(n,m+1)=(n1,…,nm,nm+1)与维护活动的位置向量Q(n,m)=(1,…,1,kl+1,…,km),其中hi+1≤ki≤ni+1,i=l+1,…,m,将问题重新描述为下面的指派问题AP(n1,…,nm,nm+1,1,…,1,kl+1,…,km): 其中 结合定理1的证明,我们给出如下求解问题(P)的算法. 算法A 步骤2 对于P(n,m+1)=(n1,…,nm,nm+1)与Q(n,m)=(k1,…,km),其中0≤ni≤n(i=1,…,m),0≤nm+1 本文研究了工件可拒绝与退化维护活动的无关机排序问题,目标是寻求退化维护活动的位置、接受工件的工件排序以及每台机器上接受工件的公共交货期,使得所有接受工件的总提前和延误惩罚与所有拒绝工件的总拒绝成本之和达到最小. 为此,我们将机器上维护活动的位置向量分为3类:(1)每台机器均在 0 时刻执行退化维护活动;(2) 每台机器均在其公共交货期di时刻之后执行退化维护活动; (3) 部分机器在0时刻执行退化维护活动,部分机器在其公共交货期di时刻之后执行退化维护活动. 根据这三种分类,分别得到3个指派问题,并借助一些代数学知识,得到该问题的多项式时间算法,时间复杂度为O(n2m+3).2 预备知识
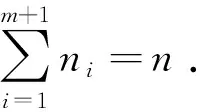


3 主要结论


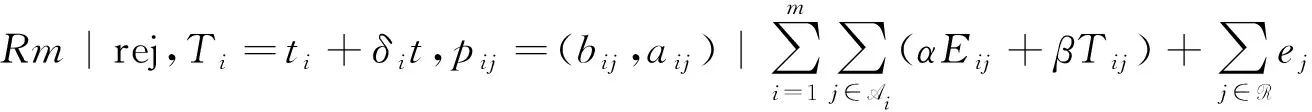
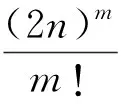
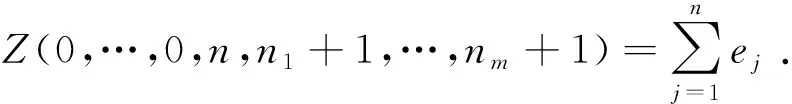

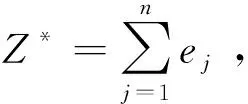
4 结 论

