机械弹性电动轮式车辆稳定性博弈协调控制

孙馨雨， 赵又群， 邓汇凡， 林 涛， 李宇昊

(南京航空航天大学 能源与动力学院， 江苏 南京 210016)

分布式驱动汽车车轮独立可控的特点是使车轮间彼此失去机械连接，可控自由度增加，操纵稳定性受到一定影响.为解决汽车底盘主动安全控制问题，常将主动前轮转向(active front-wheel steering, AFS)系统和直接横摆力矩控制(direct yaw moment control, DYC)系统进行集成控制以发挥对车辆稳定性的最大控制效果，但由于两者间存在耦合关系，在集成过程中会产生相互干扰，单一的系统叠加往往会造成功能干涉[1]，致使系统控制效果大大降低.

车辆在极限工况下的轮胎输入接近饱和，AFS系统的作用逐渐减弱[2]，失稳、驾驶员路感变差等问题随之出现.考虑平滑控制、鲁棒性好等需求，大多数研究从求得控制增益的角度来间接设计控制器，A.SAIKIA等[3]设计了二阶滑模控制器，合理选择增益系数以保证系统渐进稳定，实现了车辆轨迹跟踪. JING H.等[4]设计了H∞动态输出反馈控制器对AFS及DYC系统进行协调控制，实现了轮胎侧偏刚度、车辆纵向速度、整车质量等参数识别及车辆稳定性控制. FU Z. J.等[5]依据递归思想，提出了一种基于近似动态规划理论的无模型最优跟踪控制方法，建立了鲁棒学习规律，实现了车辆参数在线识别，提高了AFS/DYC协调控制器的精确度及鲁棒性.但控制过程繁琐，计算速度较慢.

考虑博弈论在解决多方控制问题中的良好特性，学者们根据底盘子系统间的信息交互关系，采用不同的博弈方法对子系统进行了协调控制.JI X. W.等[6]将AFS系统分别与驾驶员及ARS(active rear system)系统进行协调，以智能车转向系统交互式模型为框架，基于非合作Stackelberg博弈设计了有限时间鲁棒调节器，提高了智能车对不确定性横向扰动的鲁棒性. ZHANG Q. C.等[7]将驾驶员与DYC系统进行协调，基于动态博弈设计了无模型强化学习的横向稳定性辅助控制器.

郑鑫等[8]、赵又群[9]针对所提出的新型非充气机械弹性车轮的纵向力特性、侧偏力特性及稳定性进行了研究.DENG H. F.等[10]对机械弹性车轮(mechanical elastic wheel, MEW)装载电动机系统，制成机械弹性电动轮(mechanical elastic electric wheel, MEEW)并匹配虚拟机，在保证车辆行驶稳定性的前提下对电动机耗能问题进行研究，设计变参数线性二次型调节器(linear quadratic regulator，LQR)及非线性模型预测控制器以保持车辆稳定行驶，并采用粒子群优化算法对电动机耗能进行优化.

为研究匹配MEEW汽车在极限工况下的稳定性协调控制问题，考虑轮胎变侧偏刚度的特点，笔者基于非合作反馈Nash均衡博弈理论设计AFS/DYC协调控制器，直接输出在协调控制机制下的理想附加前轮转角和理想附加横摆力矩，并采用分层控制方法对理想附加横摆力矩进行合理分配.此控制机制可解决两子系统间相互干涉而影响稳定性控制效果的问题，并进一步提高汽车的横向稳定性.

1 基于变侧偏刚度的车辆动力学建模

1.1 二自由度动力学模型

为研究车辆行驶中的横向稳定性，考虑其侧向及横摆运动，忽略空气阻力及悬架系统的影响，建立二自由度模型，如图1所示.其中:Fy1、Fy2分别为单侧前、后轮所受侧向力；α1、α2分别为单侧前、后轮侧偏角；β、φ分别为车辆当前时刻的质心侧偏角和横摆角；lf、lr分别为车辆质心至前、后轴的轴距；l为车辆前、后轴间的轴距；vx、vy分别为车辆的纵向、侧向速度；v合为vx、vy的合速度；δf为前轮转角.

图1 车辆动力学模型

由图1可得，车辆二自由度微分方程为

(1)

式中：Cf、Cr分别为车辆前、后轮侧偏刚度；m为整车质量；Iz为车辆质心绕坐标系z轴的转动惯量.规定当车辆左转向时，前轮转角方向为正.

车辆的侧向加速度为

|ay|≤μg，

(2)

式中：μ为路面附着系数;g为重力加速度.

当车辆在极限工况下行驶，满足式(2)的前提下，其理想质心侧偏角βd和理想横摆角速度ωd分别为

(3)

(4)

式中：K为稳定性因数.

(5)

将AFS作为子控制系统，并将转向盘转角δsw作为其研究对象，以δsw=iδf的形式表示前轮转角，其中i为机械传动比.

1.2 机械弹性电动轮动力学模型

MEEW是一种新型非充气电动轮，从车轮外缘向内缘依次为橡胶层、卡环、弹性环、铰链组、轮毂盘，具有高承载能力、防爆等优点.DENG H. F.等[10]通过样机试验验证了基于魔术公式的轮胎模型能够较好地拟合出MEEW的力学特性，其力学特性试验平台及其结构示意图分别如图2、3所示，且匹配该电动轮的汽车能够正常行驶.

图2 MEEW力学特性试验平台

图3 MEEW结构示意图

轮胎侧偏刚度与其侧偏角、所受垂向力以及路面附着系数有关，即使车辆运动状态平稳，轮胎力处于线性区内，但侧偏刚度仍为变量，基于此，根据最小二乘直接法[11]，将轮胎侧偏刚度表示为

(6)

式中：j分别为左前轮fl、左后轮rl、右前轮fr、右后轮rr；α为车辆侧偏角；Fyj为轮胎所受侧偏力.

考虑侧偏角αj为0的情况，使用分段函数表示侧偏刚度，即

(7)

式中：k为曲线在αj=0处的斜率.

车辆前、后轮侧偏刚度分别为

(8)

由魔术公式可得轮胎所受侧偏力：

Fy=Dysin{Cyarctan{ByX1-Ey[ByX1-

arctan(ByX1)]}}+Sv=Dysin{Cyarctan{By(αj+

Sh)-Ey{By(αj+Sh)-arctan[By(αj+Sh)]}}}+Sv，

(9)

式中：Sh、Sv分别为水平方向漂移和垂直方向漂移；By、Cy、Dy、Ey分别为车辆侧向的轮胎刚度因子、形状因子、峰值因子、曲率因子.

Sh、Sv在极限工况下可忽略不计，By、Cy、Dy、Ey由MEEW样机试验数据拟合得到，如表1所示.其中：Fz为径向载荷；Bx、Cx、Dx、Ex为纵向的轮胎刚度因子、形状因子、峰值因子、曲率因子.

表1 魔术轮胎公式拟合参数

2 基于Nash均衡博弈的AFS/DYC协调控制

2.1 控制系统的结构

设计了基于李雅普诺夫的最优子控制器，在此基础上设计了基于Nash均衡博弈的上层协调控制器和基于二次规划的力矩分配下层控制器，整车稳定性控制系统设计原理如图4所示.其中Txj为四轮驱动转矩.博弈协调控制器以保证AFS子控制器和DYC子控制器独立实现车辆稳定性控制为前提，根据两者的控制策略对两子系统信息进行实时交互，最终计算出协调控制机制下的Nash均衡解(U1*,U2*)通过叠加理想附加转向盘转角Δδsw*对车辆进行转向干预，合理分配理想附加横摆力矩ΔM*,使车辆质心侧偏角和横摆角速度跟踪稳定状态下的理想值，提高车辆在极限工况下的横向稳定性.

图4 整车稳定性控制系统设计原理图

2.2 AFS与DYC子控制器设计

以状态空间方程的形式表达车辆质心侧偏角偏差Δβ及横摆角速度偏差Δω，表达式为

(10)

其中：

(11)

根据李雅普诺夫能控性判据，设

Z=Γc(A(α),B(α))=[B(α)A(α)B(α)]，

易知Z为2×4阶矩阵，由

rank(Z)=2

可知，Z矩阵满秩，满足系统可控的必要条件，因此系统可控.定义AFS、DYC子控制器的性能指标函数为

(12)

式中：k=1代表AFS子控制器；k=2代表DYC子控制器；Qk、Rk为各子控制器的权重矩阵.

由子控制器独立控制所得到的系统最优解为

(13)

式中：Pk为黎卡提方程的解.

黎卡提方程为

AT(α)Pk+PkA(α)+Qk-

(14)

2.3 上层博弈协调控制器设计

2.3.1Nash均衡博弈理论

博弈论考虑参与者的预测行为与实际行为，并研究各自的优化策略.博弈过程实际是一场行为信号实时交互过程[12]，在一场有q个参与者进行的博弈中，每个参与者持有各自的博弈策略，并会在每局博弈结束后得到各自的博弈结果.博弈结果不尽相同，在其不断变化的过程中，存在一组解集{U1*,U2*,…，Uq*}使得所有参与者最终得到较稳定且较高的效益，其中，Uq*为q个参与者各自的博弈理想解.当参与博弈的任意一方改变自身博弈策略后，所有参与者都无法获得比解集中结果更优的博弈结果.

根据参与者之间是否存在约束力，分为合作博弈与非合作博弈；根据参与者进行决策的先后顺序，分为静态博弈与动态博弈；根据参与者之间是否完全将自身信息进行交互，分为完全信息博弈和不完全信息博弈.基于此，对AFS与DYC的协调控制问题进行分析，可得博弈过程与协调控制过程之间存在如下联系：

1) 在AFS与DYC协调控制过程中，两者控制目标相同，假定任意一方不会单独改变控制策略，并期望自身的成本函数都能达到最优，此行为属于博弈过程，因此两者等同于博弈参与者.

2) AFS和DYC对车辆稳定性的控制作用相互独立，不存在相互制约力，此协调过程属于非合作博弈；两者信息交互时间序列间隔很小，可忽略不计，此过程属于静态博弈；在此交互过程中，DYC系统及AFS系统均能够得到对方的全部信息，此过程属于完全信息博弈.

综上可知，AFS/DYC协调控制过程属于完全信息静态博弈，因此利用Nash均衡概念对AFS及DYC的协调控制问题进行分析，使得博弈达到最终稳定结果的策略集称为Nash均衡偶.

2.3.2基于博弈论的上层协调控制器设计

根据对非合作博弈理论与AFS/DYC协调控制机理的阐述，结合Nash均衡偶的性质可得

(15)

式中：U1*=Δδsw*和U2*=ΔM*分别为两者在Nash均衡点处博弈所产生的理想博弈结果.

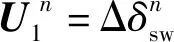
(16)

将式(16)中的输入项改写为耦合项得到

(17)

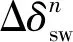
协调控制系统的理想解为

(18)

式中：Rkk为两子系统自身的定权重矩阵；Kk为状态反馈矩阵；Uk*与Nk呈线性变化关系；Nk为耦合黎卡提方程的解.

耦合黎卡提方程的解为对称正定矩阵，即

(19)

其中：

(20)

由于李雅普诺夫稳定性正定二次型能量函数为

V=XTNkX≥0，

(21)

但是

KkTBT(α)Nk+NkA(α)-NkB(α)Kk)X=

(22)

因此，X=0为系统的稳定平衡点，由李雅普诺夫直接法可知，所设计的博弈协调控制器稳定，可用于车辆行驶稳定性控制.

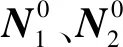
(23)

进行迭代循环计算的方程为

(24)

收敛条件为

(25)

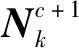
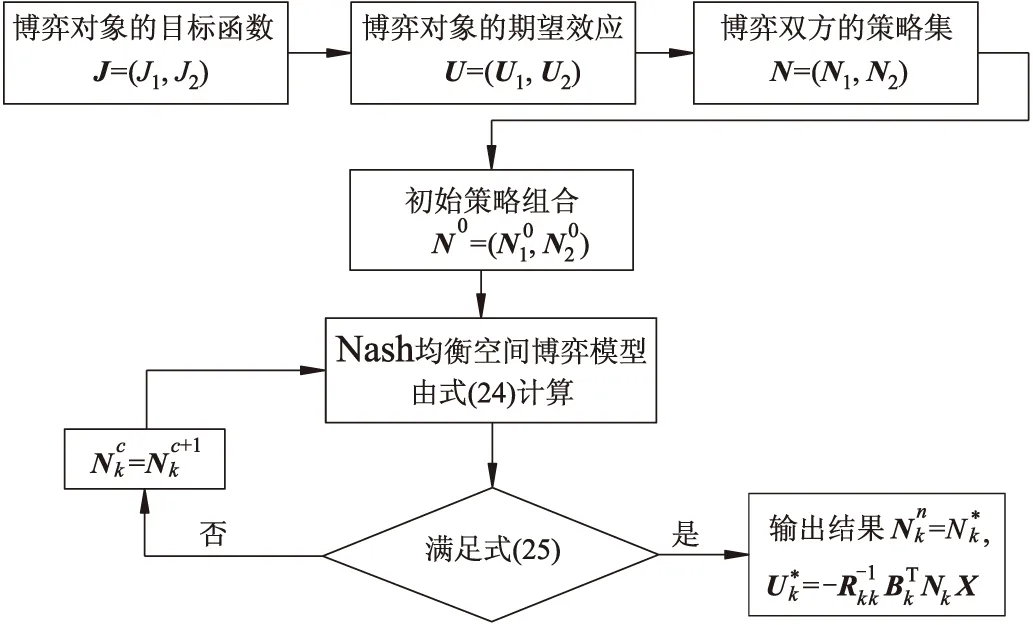
图5 多输出理想结果的博弈流程图

2.4 基于二次规划的下层分配控制器设计

由上层博弈协调控制器直接产生的ΔM*无法直接作用于车辆驱动轮，需要下层执行机构对其进行分配并传递至电动机处，完成控制系统对车辆横摆运动的修正.以轮胎利用率之和最小为控制目标，以电动机峰值转矩为约束条件，规定车辆横摆角速度逆时针方向为正，根据车辆驱动总力矩与驱动轮驱动力矩之间的关系，构造二次规划问题的数学表达式，对轮胎力进行合理分配：

(26)

式中：ε为轮胎附着利用率；Fzj为轮胎所受垂向力；R为MEEW的有效滚动半径；Tx为车辆驱动总力矩；tf、tr分别为车辆的前轮距和后轮距；Tm_max为电动机峰值转矩.

3 CarSim/Simulink联合仿真及分析

利用CarSim软件对匹配MEEW的某型乘用SUV的Simulink模型进行联合仿真，该汽车主要参数如下：m=1 590 kg；lf=1.18 m；lr=1.77 m；Iz=2 687.1 kg·m-2；质心至地面高度h=0.72 m；tf=1.799 m；tr=1.693 m；g=9.81 m·s-2.博弈协调控制器参数如下：AFS系统的权重矩阵Q1= diag(1 000,1 000)；DYC系统的权重矩阵Q2= diag(5×106,5 000)；AFS系统自身的权重矩阵R11=diag(1,1)；DYC系统自身的权重矩阵R22= diag(1,1)；ΔM对AFS的影响权重矩阵R12=0.000 1；Δδsw对DYC的影响权重矩阵R21=0.000 1；采样周期为0.005 s.

设置车速为100 km·h-1、路面附着系数为0.3的双移线工况，对博弈协调控制器控制、AFS/DYC叠加控制、AFS单独控制、DYC单独控制以及无控制器等控制机制下的车辆稳定性相关参数进行了对比验证，仿真结果如图6-12所示.不同控制作用的车辆行驶轨迹跟踪效果如图6所示.

图6 不同控制作用的车辆行驶轨迹跟踪效果

从图6可以看出：在无控制器控制机制下，车辆在行驶到140 m时出现峰值，且后续无法再回归至原设定路径中，说明车辆在转向过程中发生侧滑并逐渐偏离轨迹；在加入任意控制器后，其行驶轨迹逐渐靠近设定路径，由博弈协调控制器控制的车辆最接近规划路径，路径跟踪效果优于单一叠加子控制器的跟踪效果.

不同控制作用的纵向速度跟踪效果如图7所示.在无控制器控制机制下，曲线在3.5 s处开始下降，在6.2 s处回升，在7.3 s处再次下降；车辆在由3.5 s至6.2 s期间完成2次转向后发生失稳，vy提高，导致vx降低；当车辆在7.3 s处进行第3次转向时已完全失稳并发生甩尾；在AFS控制机制下，车辆仍在第3次转向时出现较大跌落，说明甩尾现象仍然存在；在DYC控制机制下，车辆稳定性有效提高，说明极限工况下的车辆轮胎附着力极小，AFS对车辆单独干预的作用极小，DYC起到主要控制作用；相比之下，博弈协调控制机制下的曲线更加贴近理想车速，且与理想值相差不超过0.35 m·s-1，说明博弈协调控制器对车辆稳定性的控制效果最佳.

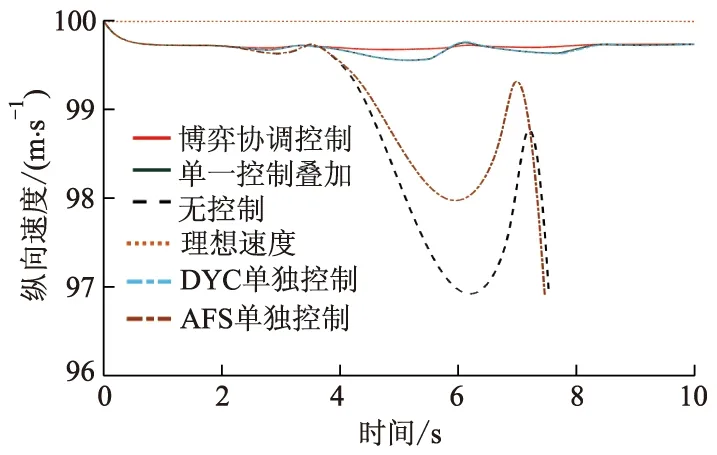
图7 不同控制作用的纵向速度跟踪效果

不同控制作用的转向盘转角仿真结果如图8所示.在无控制器控制及AFS控制机制下，曲线在2.5 s及7.0 s处经历了很大波动，说明车辆失稳并发生甩尾后，转向盘作用失效，并随着车辆运动状态改变而发生极大转动；在其他控制机制下，δsw逐渐降低，其中，博弈协调控制器控制作用最好，可使最终结果稳定在±20°左右.在博弈协调控制及DYC控制机制下，曲线在车辆转向以及转向盘回正过程中均出现了小波动，这是由于轮胎力即使处于线性范围内，轮胎侧偏刚度仍然会有变化，而MEW本身的构造使得其侧偏特性存在不确定摄动[8]，该振动通过传动系反馈至转向盘，造成转向盘抖动.

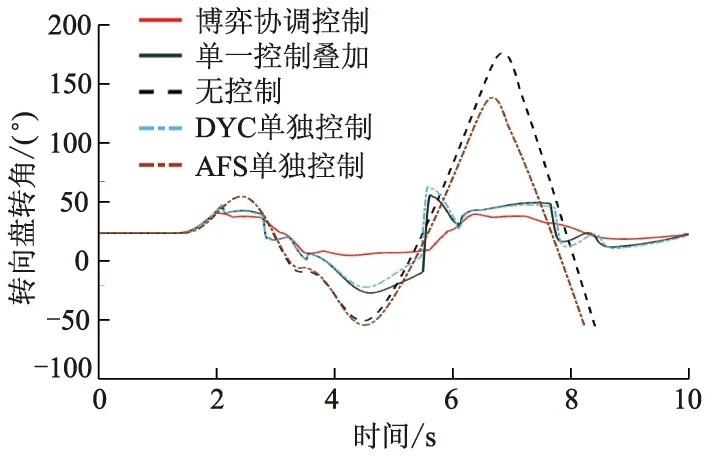
图8 不同控制作用的转向盘转角仿真结果

不同控制作用的质心侧偏角仿真结果如图9所示.在无控制及AFS控制机制下，质心侧偏角β的峰值超过10°，即使加入DYC控制器，甩尾现象仍然存在.只有在博弈协调控制器的控制机制下，β才能稳定在1°以内，并与理想值相差0.48°～0.81°，进而跟踪横摆角速度来控制车辆的行驶稳定性.

图9 不同控制作用的质心侧偏角仿真结果

不同控制作用的横摆角速度仿真结果如图10所示.由博弈协调控制器控制的横摆角速度ω为所有控制机制下最小，但该控制机制下的ω变化范围比理想值ωd变化范围小，车辆跟踪理想横摆角速度的误差为0.035～0.425 (°)·s-1.由此可知，为保持车辆稳定行驶，协调控制器会使车辆尽量减小横摆程度，因此对工况设定路径的跟踪效果并不是最优，但其最接近理想值时的跟踪误差，其值不超过0.05 (°)·s-1.

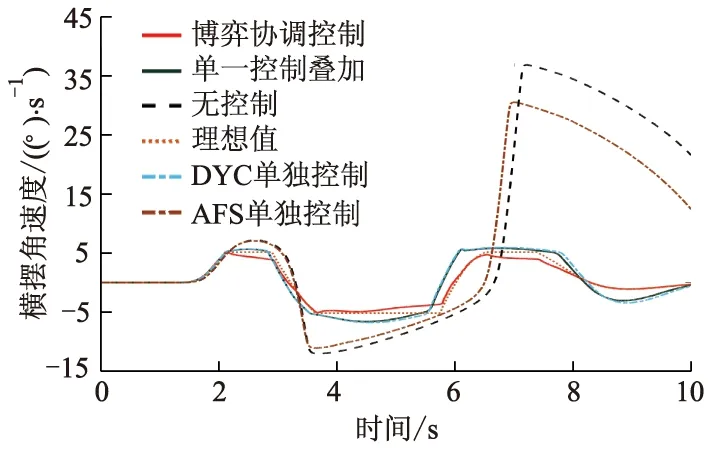
图10 不同控制作用的横摆角速度仿真结果

不同控制作用的附加横摆力矩仿真结果如图11所示.DYC控制效果较差，因此对应的附加横摆力矩ΔM变化也较大；AFS不单独参与车辆横摆运动的控制，但在控制器叠加控制中其仍发挥一定作用.DYC和AFS叠加控制而产生的ΔM相比DYC单独控制时的ΔM稳定，其曲线的波动程度在车辆前2次转向时轻于博弈协调控制器，但在第3次转向时却出现更大波动，这是由于两子控制器的反馈矩阵为定值，当车辆在前两次转向发生侧滑时，反馈矩阵的参数无法根据车辆的实时运行状态做出相应调整，而博弈协调控制器能够对输出的结果不断进行博弈，具有动态调整性质，因此其控制作用仍然比子控制器单一叠加的效果好.

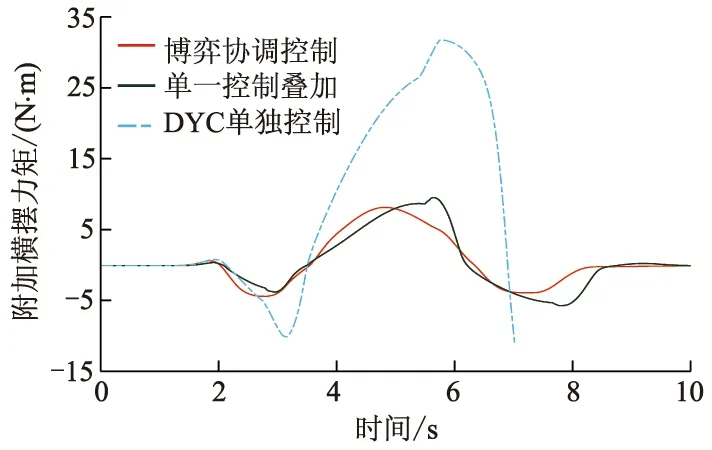
图11 不同控制作用的附加横摆力矩仿真结果

不同控制作用的相位图对比如图12所示.加入任意控制器后，ω及β均处于可控范围内，系统处于稳定状态，而博弈协调控制器控制机制下的相位图收敛程度最高.

图12 不同控制作用的相位图对比

综上可知，博弈协调控制器通过实时交互AFS与DYC独立控制车辆稳定性时的控制信息，能够实现两者的协调控制，具有实时性.仿真结果表明：该协调控制器的控制效果相较子控制器单一叠加时的控制效果好，能够保证车辆在极限工况下的行驶稳定性.

4 结 论

1) 博弈协调控制器能够结合个体控制策略对AFS与DYC进行实时信息交互，其本质是为求得理想输出解而进行的循环计算过程，该控制机制能够使车辆得到更高的路径跟踪能力.

2) 博弈协调控制器跟踪车辆理想质心侧偏角及理想横摆角速度的误差分别为0.48°～0.81°和0.035 ～0.425 (°)·s-1，该控制机制能够使车辆得到更高的稳定性.