基于传感器信息融合的车辆位姿估算方法

李臣旭， 江浩斌， 王成雨， 马世典

(1. 江苏大学 汽车与交通工程学院， 江苏 镇江 212013； 2. 江苏大学 汽车工程研究院， 江苏 镇江 212013)

智能车辆作为智能交通系统的重要组成部分，其关键技术的研究已成为国内外科研机构关注的焦点.自动泊车是智能车辆关键技术的研究热点之一，其中车辆位姿的精确定位是实现智能车辆自动泊车的一项关键技术，它是实现对泊车路径精准跟踪的前提，更是提高泊车精度的关键[1].

自动泊车过程中，系统识别到目标车位后会控制车辆按照规划好的路径泊车入位，常规泊车控制方法是以车辆位姿的跟踪误差作为输入，该误差指车辆在参考坐标系中位姿与规划路径之间的误差[2].在对控制方法进行仿真验证时，通常认为车辆实际位姿已知.在实际泊车场景中，车辆的相对位姿无法直接获知，需要通过车载传感器获取的周边环境信息以及车辆的自身运动状态推算出车辆的当前位姿信息.

车辆的位姿定位方法主要分为相对定位法和绝对定位法.相对定位法利用的是车辆内部传感器观测车辆本身的状态信息，并由当前时刻的位姿状态去估算下一时刻的状态，例如基于惯性导航系统和基于里程计的定位方法.这种方法的优点是根据车辆运动学方程和传感器反馈的当前车辆运动状态即可估算出该时刻车辆的位姿变化，缺点是车辆状态信息均通过传感器获取，系统误差不可避免，累积误差降低了车辆的定位精度[3].绝对定位法是利用车上安装的传感器感知车辆周边环境信息，从而估算出车辆在当前环境中所处的绝对位姿，例如基于GPS(global positioning system)的定位、基于地图匹配的定位以及基于视觉的定位等.这种方法的优点是能够获取丰富的环境信息，易于获取车辆的位姿信息，实现车辆的全局定位，但缺点是对传感器的精度要求较高，实现成本较高，且处理的数据量较大，实现定位的算法较为复杂[4].

对于车辆的位姿估计技术的研究，成果多集中在移动机器人定位领域，泊车系统位姿估计方法的研究尚较少.J. BORENSTEIN[5]利用里程计实现移动机器人的位姿估计，通过定位误差分析发现，轮径不等以及轴距长度的不确定性为主要误差来源，并利用定时的绝对位置更新提高定位精度.李力等[6]利用单目视觉传感器，通过对地面标靶的特征提取与EPnP的方法求解相机位姿，以实现对飞行机器人位姿的估计.丰俊丙[7]基于视觉传感器开展了移动机器人自定位以及目标物位姿测量技术的研究，通过机载相机和物体空间姿态估计算法计算出标志物的相对距离和方位，然后结合标志物位置信息利用扩展卡尔曼滤波算法估算得到机器人在世界坐标系中的位置.罗勇等[8]利用车辆两后轮的轮速传感器信号与前轮转角信号，通过卡尔曼滤波算法对车辆的位姿进行估计，实现了较高的车辆位姿估计精度，并将方法利用到自动泊车中.

近年来，随着智能辅助驾驶技术研发的不断升温，用于环境感知与车辆自身定位的传感器类型也逐渐增多，通过传感器融合技术以及相关的滤波算法实现对车辆精准定位，在该领域的应用越来越广泛，基于单一定位方法实现车辆位姿定位的局限性被进一步放大.利用智能汽车中的多种传感器数据进行信息融合，可以有效弥补单一采用上述任一位姿定位方法的不足，更好地实现车辆定位定姿，且能够极大地降低系统对于周边设施的依赖程度，从而提高自动泊车系统的智能化水平和对复杂环境的适应性，因此，基于传感器信息融合的车辆位姿定位成为高智能化自动泊车系统技术的发展趋势[9-11].

笔者采用融合轮速传感器信息与视觉传感器信息的方法，对泊车过程中车辆位姿的估算方法进行研究.首先利用轮速传感器对车辆位姿进行估算，并分析误差产生的原因；然后利用视觉传感器信息与轮速传感器信息进行融合，减小系统误差，提高车辆位姿估算准确性；最后进行仿真试验，验证提出的位姿估算方法的有效性.

1 航迹推算位姿估算

航迹推算位姿估算是利用传感器信息估算车辆的相对运动位姿，笔者利用车辆ABS/ESC(antilock brake system/electronic stability controller)系统中安装于两后轮的轮速传感器，结合车辆当前时刻位姿与传感器的数据，推算出车辆下一时刻的位姿.航迹推算的算法实现简单，且成本较低，但是位姿估算结果受累计误差的影响，随着时间的推移，位姿估算的置信度随之降低.

1.1 车辆运动学模型

利用里程计估算车辆的位姿，属于二维空间的位姿问题.以时间为参考，结合车辆线位移、角位移以及前一时刻的位姿对现在的位姿进行估算，属于二维空间的位姿问题.笛卡尔坐标系下离散化的汽车运动学模型如图1所示，车辆后车轴中心点在k时刻的位置为(xk,yk)，航向角为θk.

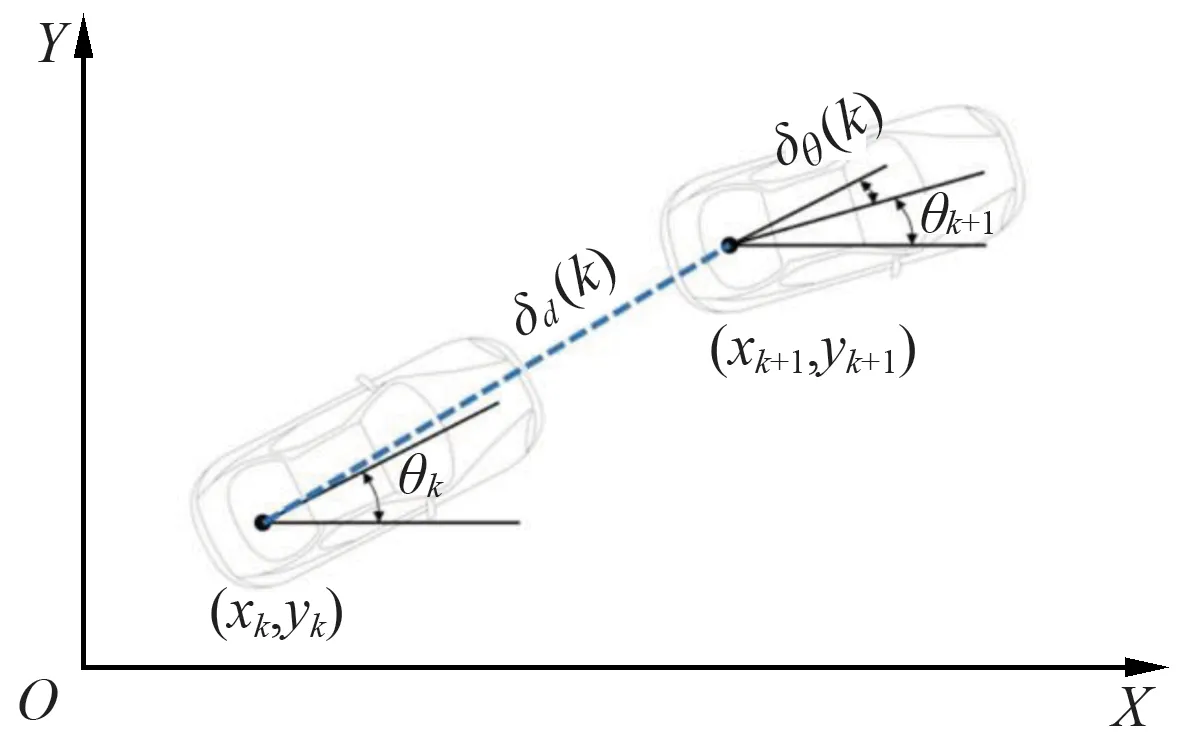
图1 车辆运动模型

车辆在第k时刻的位姿为

(1)

由于系统的取样时间是一个很小的值，车辆在一个时刻内的位姿变化可以分解为车辆的位移δd和转过的角度δθ，第k个时刻内位姿改变表示为δ(k)=[δd(k),δθ(k)]T，位姿变化的过程可以近似等效为车辆先绕后轴中点的转动，后进行平移.k+1时刻，车辆先绕后轴中点旋转δθ后的车辆位姿为

(2)

车辆位移δd后的位姿为

(3)

k+1时刻的位姿用向量形式表示为

(4)

1.2 里程计定位

利用轮速传感器来获取汽车的δd和δθ，车轮行驶过的距离为

(5)

式中：n为记录的上升沿个数；r为车轮的滚动半径；N为齿圈的总齿数.

车辆的δd和δθ均可通过两车轮行驶里程表示：

(6)

式中：dl、dr分别为车辆左后轮和右后轮行驶的里程；nl、nr分别为两轮齿圈转过的齿数；l为车辆后轴有效长度.

将式(6)所得结果代入式(4)，即可得到车辆在k+1时刻的位姿，但前提是所测得的里程是完全准确的.实际应用中，里程计的测量结果会受到多种误差影响，主要分为系统误差和随机误差2种，其中：系统误差主要包含车位滚动半径误差、轮距测量误差和转子码盘分辨率误差等；随机误差主要来源于车轮与地面的滑动、轮胎载荷变化以及受路面不平度影响等因素.

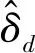
(7)

将式(7)代入式(4)可得车辆的真实位姿为

(8)

2 融合视觉信息的车辆位姿估算

航迹推算的位姿估算方法由于受到测量噪声的影响，估算的位姿和实际位姿之间存在一定偏差，同时随着时间推移，仅依靠之前的位姿及不太准确的传感器结果进行估算，会使该测量值的不确定性进一步增大，累积误差也随之增加，为解决该问题，需要引入新的观测信息.利用视觉传感器来获取车辆的周边环境信息，通过扩展卡尔曼滤波算法对视觉传感器信息和轮速传感器信息进行融合，降低测量噪声对位姿误差的影响，提高车辆位姿信息的估算精度.

2.1 卡尔曼滤波与信息融合方法

2.1.1卡尔曼滤波

对于一个动态的线性离散系统，系统方程定义为

xk=Fk-1xk-1+Gk-1uk-1+vk-1,

(9)

式中：xk、xk-1分别为该系统的k、k-1时刻的状态向量；Fk-1为k-1时刻的系统矩阵；Gk-1为k-1时刻的输入矩阵；uk-1为k-1时刻的系统输入向量；vk-1为k-1时刻的系统测量的随机误差向量.

假设有一观测器，对系统的状态进行观测，观测方程定义为

yk=Hkxk+wk,

(10)

式中：yk为k时刻的观测向量；Hk为k时刻的观测矩阵；wk为k时刻观测的随机误差向量.

卡尔曼滤波的具体运算过程如下：

初始化滤波器为

(11)

式中：E表示取期望，若有确定的初始位置x0，那么系统的初始协方差P0+=0，但若x0也是一个随机变量，那么P0+则是这个随机变量的协方差矩阵.

系统状态的先验为

(12)

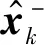
系统状态的更新，卡尔曼增益矩阵为

(13)

式中：Wk为观测误差协方差矩阵.

后验估算为

(14)

式中：I为单位矩阵.

需要注意的是，上述卡尔曼滤波的推算过程只能运用在线性离散系统中，车辆的定位问题属于非线性系统，本研究使用基于扩展卡尔曼滤波(extended Kalman filter,EKF)方法，通过对矩阵函数进行泰勒展开，取其展开式第1项将系统转化为近似线性系统.

2.1.2信息融合

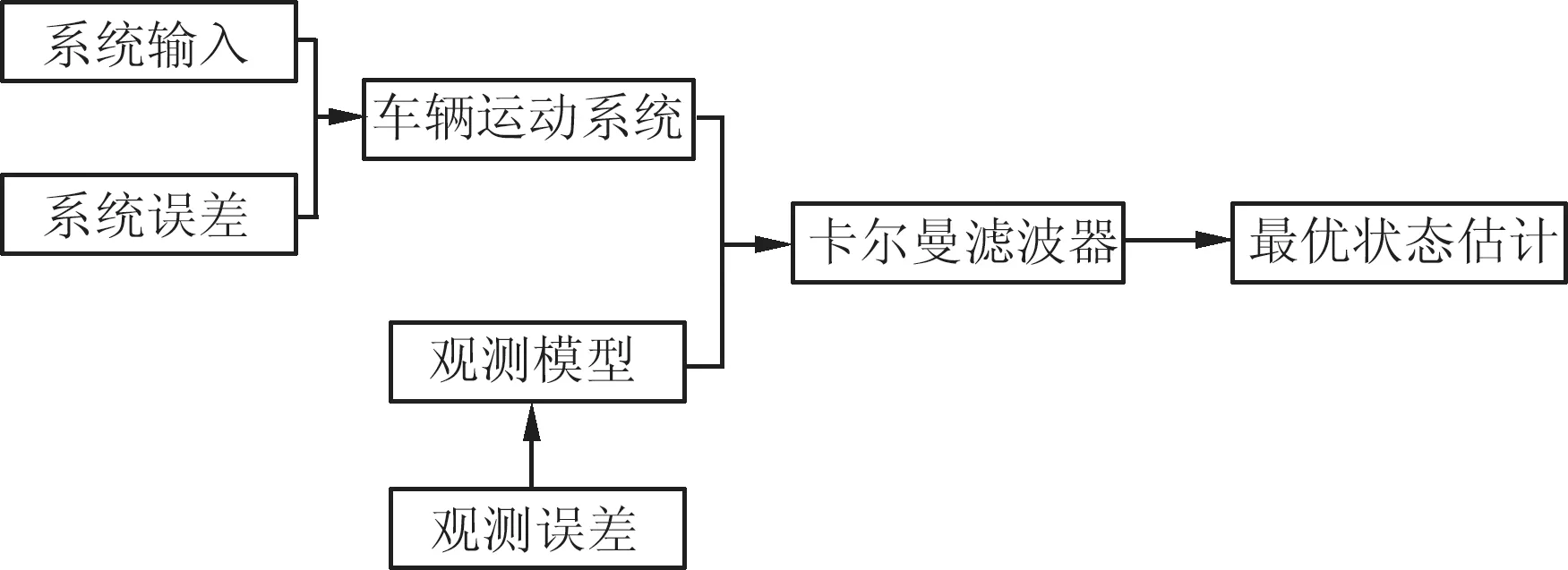
图2 位姿估算的信息融合方法

2.2 基于扩展卡尔曼滤波算法的位姿估算

视觉传感器作为环境感知单元，在自动泊车系统中所起的作用除了要能实现车位的识别，还需对车辆与目标车位的相对位置进行计算.但视觉传感器易受环境的干扰，例如光线、雨雾等，且受到像素和分辨率的影响，所以仅依靠视觉传感器进行车辆的位姿估算并非完全准确[12].基于上述分析，利用扩展卡尔曼滤波算法，结合轮速传感器和视觉传感器的融合信息，对自动泊车过程中的车辆位姿进行估算.

2.2.1系统模型

由式(8)可得车辆运动学方程为

Xk+1=f(Xk,δk,vk),

(15)

式中：Xk=(xk,yk,θk)T为车辆在k时刻的位姿状态向量；δ(k)=(δd(k),δθ(k))T为传感器测得的位姿变化向量；vk=(vd(k),vθ(k))T为传感器测量噪声.

测量噪声v可认为满足高斯分布的随机变量，即

v=(vd,vθ)～N(0,V),

(16)

测量噪声的协方差矩阵为

(17)

式中：σd、σθ分别为位移方差与航向角方差.

(18)

式中：Fk和Lk分别是对矩阵函数进行求导后所得的雅可比矩阵.

在vk=0时，Fk和Lk可表示为

(19)

2.2.2观测模型

通过视觉传感器获取观测信息，观测模型如图3所示.

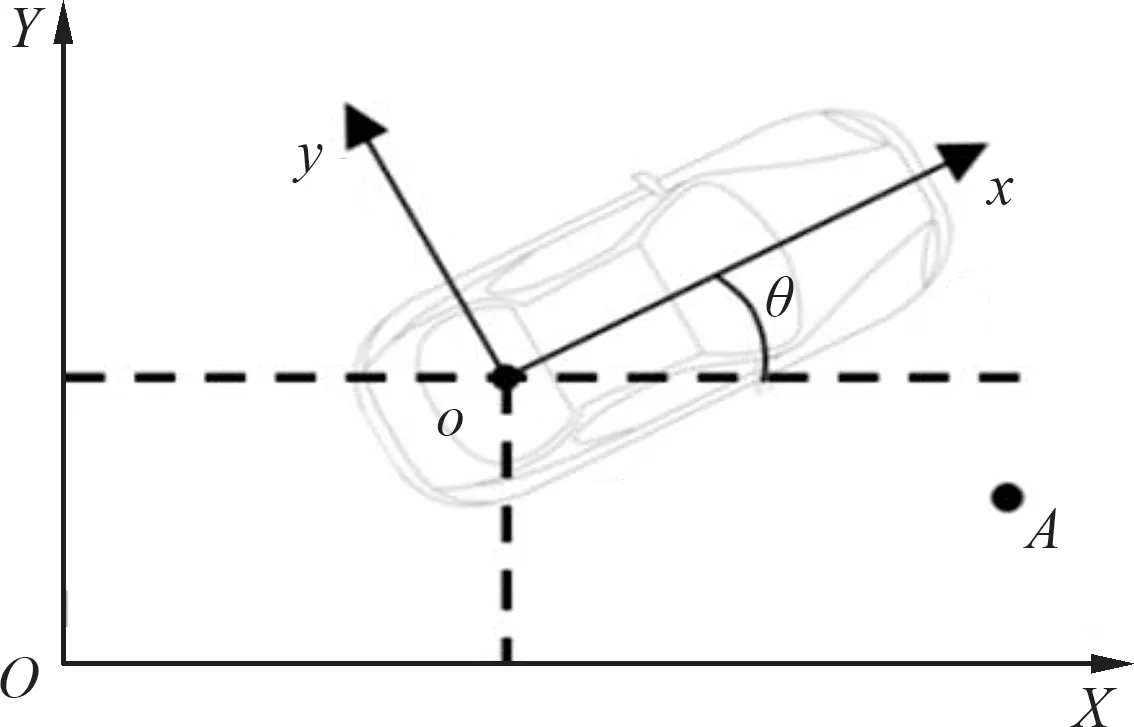
图3 系统观测模型

由于观测点与车辆都在地平面上，所以这是个二维位姿问题.其中：OXY为世界坐标系；oxy为车辆坐标系；A为空间中的观测点，目标车位线角点可以作为图像中被观测的特征点，(x,y,θ)T为车辆在世界坐标系中的位姿.点A在地面世界坐标系上的坐标和在车辆坐标系中的坐标之间的关系为

(20)

式中： (VxA，VyA，1)为A在车辆坐标系中的齐次坐标; (WxA，WyA，1)为A在世界坐标系中的齐次坐标.

世界坐标系和车辆坐标系之间的位姿关系为

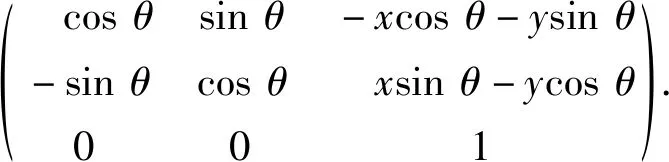
(21)

对图像进行去畸变与逆透视变换，将图像转化为对地面的俯视图，车辆坐标系OxVyV与图像坐标系oxPyP之间的关系如图4所示.

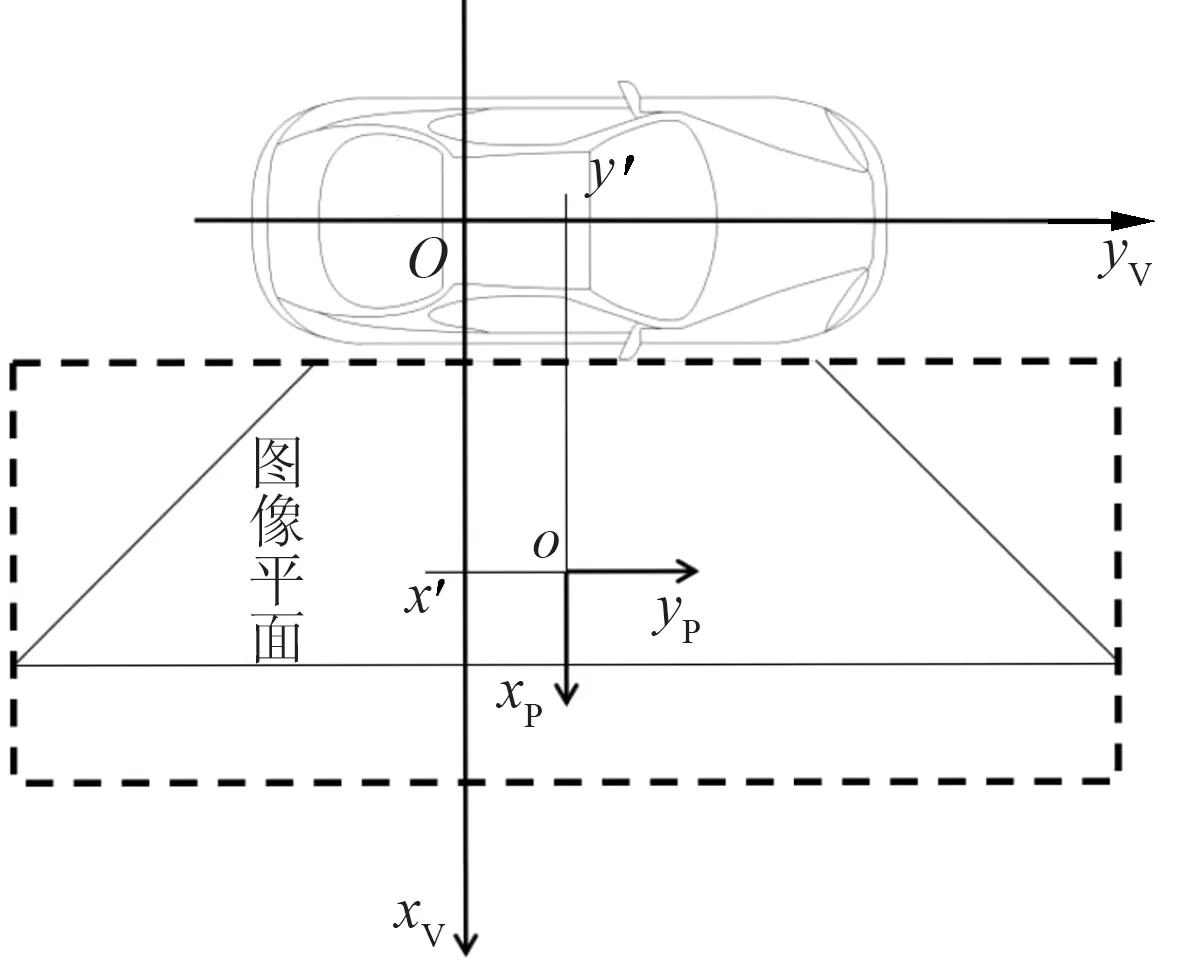
图4 车辆坐标与图像坐标

图像坐标系与车辆坐标系之间仅有缩放与位移，故A点的坐标关系可表示为

(22)

式中：s为缩放比例系数；x′、y′为坐标系的位移量.

由式(22)可得基于视觉传感器观测结果为

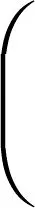
(23)

对于观测方程，由于图像会受到噪声影响，且摄像头固定在车身上易受到车身振动的影响，进一步影响观测结果，对包含噪声的观测方程可表示为

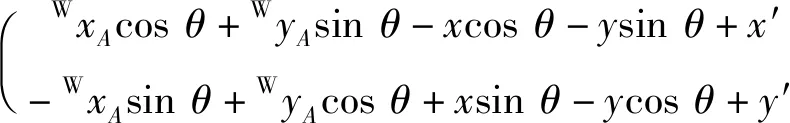
(24)

测量噪声可认为满足高斯分布的随机变量：

w=(wx,wy)～N(0,W).

(25)

(26)

式中：W为测量协方差矩阵；σx、σy为位移在x、y方向上的观测方差.

综上，观测模型在k时刻的函数形式为

zk=h(Xk,wk).

(27)

(28)

雅可比矩阵Hk、Mk可表示为

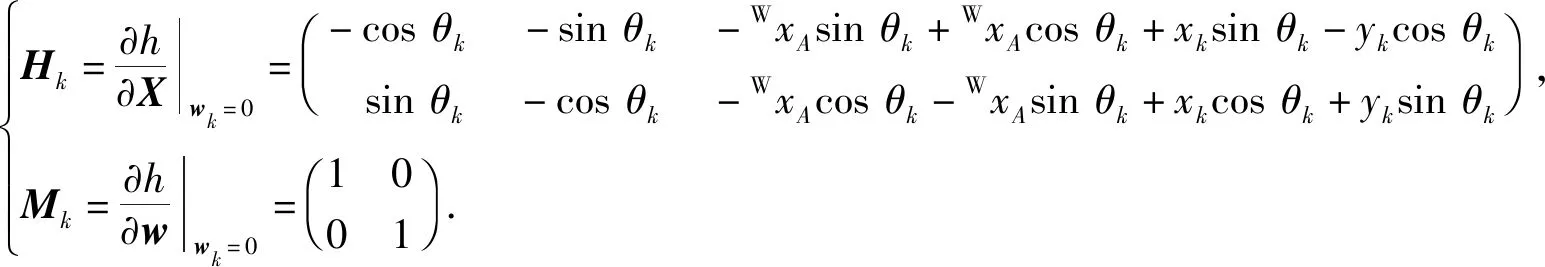
(29)

2.2.3位姿估算

在k+1时刻，车辆位姿的先验与此时的协方差矩阵可以用上一时刻的后验结果表示，即

(30)

先验结果是不包含观测信息的预测结果，利用视觉传感器获取观测信息对状态先验进行修正，从而得到车辆位姿的后验结果与协方差，这个结果就是k+1时刻经过卡尔曼滤波后的位姿估算值与其协方差矩阵，修正过程可表示为

(31)

式中：Kk+1为k+1时刻的卡尔曼增益矩阵；εk+1为k+1时刻的观测残差.

k时刻卡尔曼增益矩阵为

(32)

k时刻的观测残差为

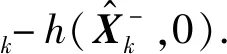
(33)

3 位姿估算仿真试验

为验证算法的有效性，首先建立车辆运动学仿真模型、相机模型和轮速传感器模型，然后控制车辆沿设定的轨迹进行运动，最后通过Simulink建立位姿估算模块模型并设定相关参数进行仿真试验，验证设计方法对车辆位姿的估算效果.

3.1 车辆运动学模型的建立

基于某SUV(suburban utility vehicle)车型开展算法验证，车辆的相关尺寸参数如下：车长为4.788 m；车宽为1.933 m；轴距为2.850 m；前悬长为0.966 m；后悬长为0.972 m；前轴轮距为1.641 m；后轴轮距为1.642 m；前轮最大等效转角为0.541 rad；最大前轮转角速度为0.541 rad·s-1；车辆最大加速度为4.2 m·s-2.

基于试验车参数在Simulink中建立车辆的运动学模型，如图5所示.通过对车速与前轮转角的输入，输出车辆的位姿状态(x,y,θ)T.

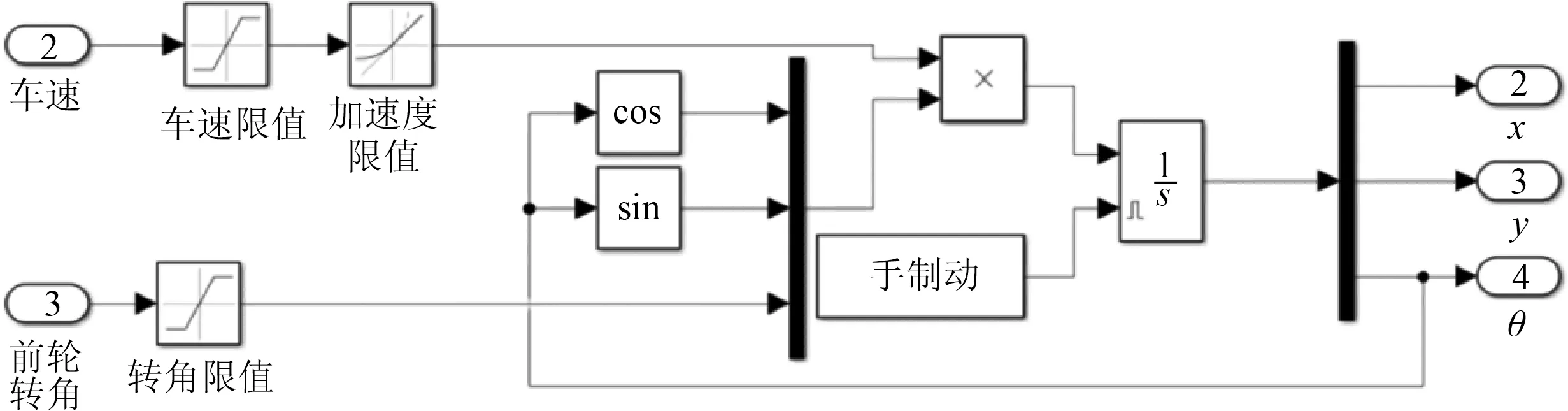
图5 车辆运动学仿真模型

3.2 相机模型的建立

为实现对车身周围进行全方位的环境感知，视觉信息采集是基于四路摄像头的环视图像，生成车辆的环视俯视图.相机模型利用Simulink中的FSN模块实现，如图6所示.

图6 相机模型

通过调用Matlab的相机成像函数，实现相机模型的输入输出功能，相机模型的输入为点在相机坐标系中的坐标，输出为点在成像平面上的坐标.

3.3 轮速传感器模型的建立

轮速传感器对车辆位姿估算模型如图7所示，其中：uv为车辆行驶的速度；k为放大倍数.输入为车辆位姿(x,y,θ)T，输出为传感器测得的相对位姿变化向量δ.

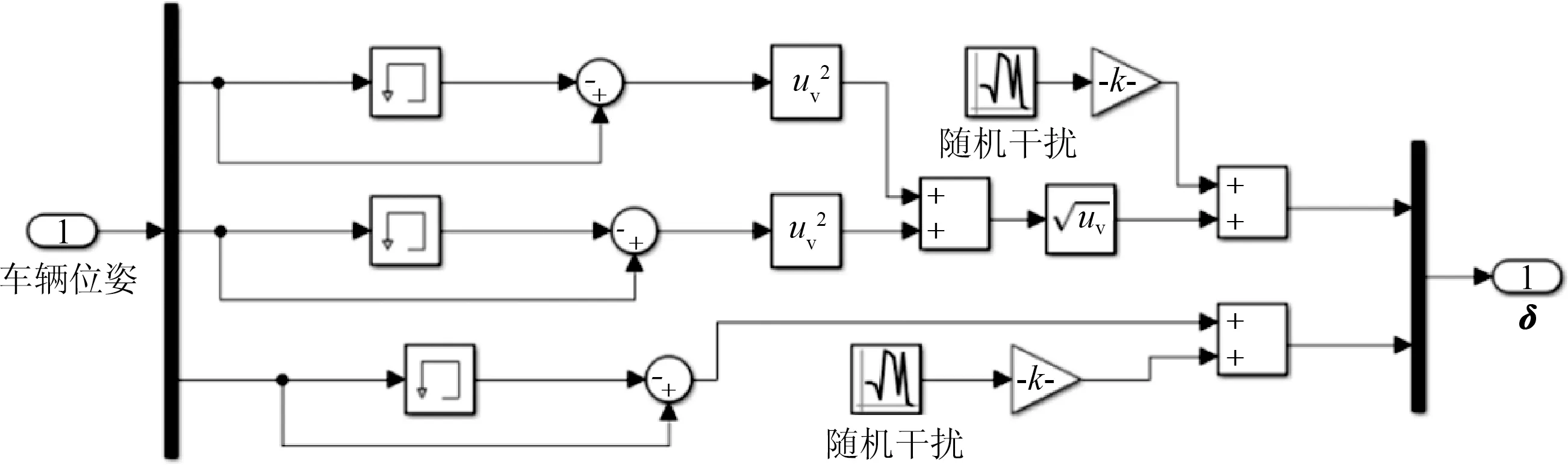
图7 轮速传感器仿真模型

3.4 位姿估算模型的建立

利用Simulink中的FSN模块对传感器融合的位姿估算算法进行封装，构成车辆信息融合位姿估算模块，如图8所示.利用视觉传感器观测模型z和基于轮速传感器的车辆运动状态向量作为输入δ，结合车辆的初始状态，通过EKF模块，最后输出车辆位姿状态的估算值(xest,yest,θest)T与系统的协方差Pest.

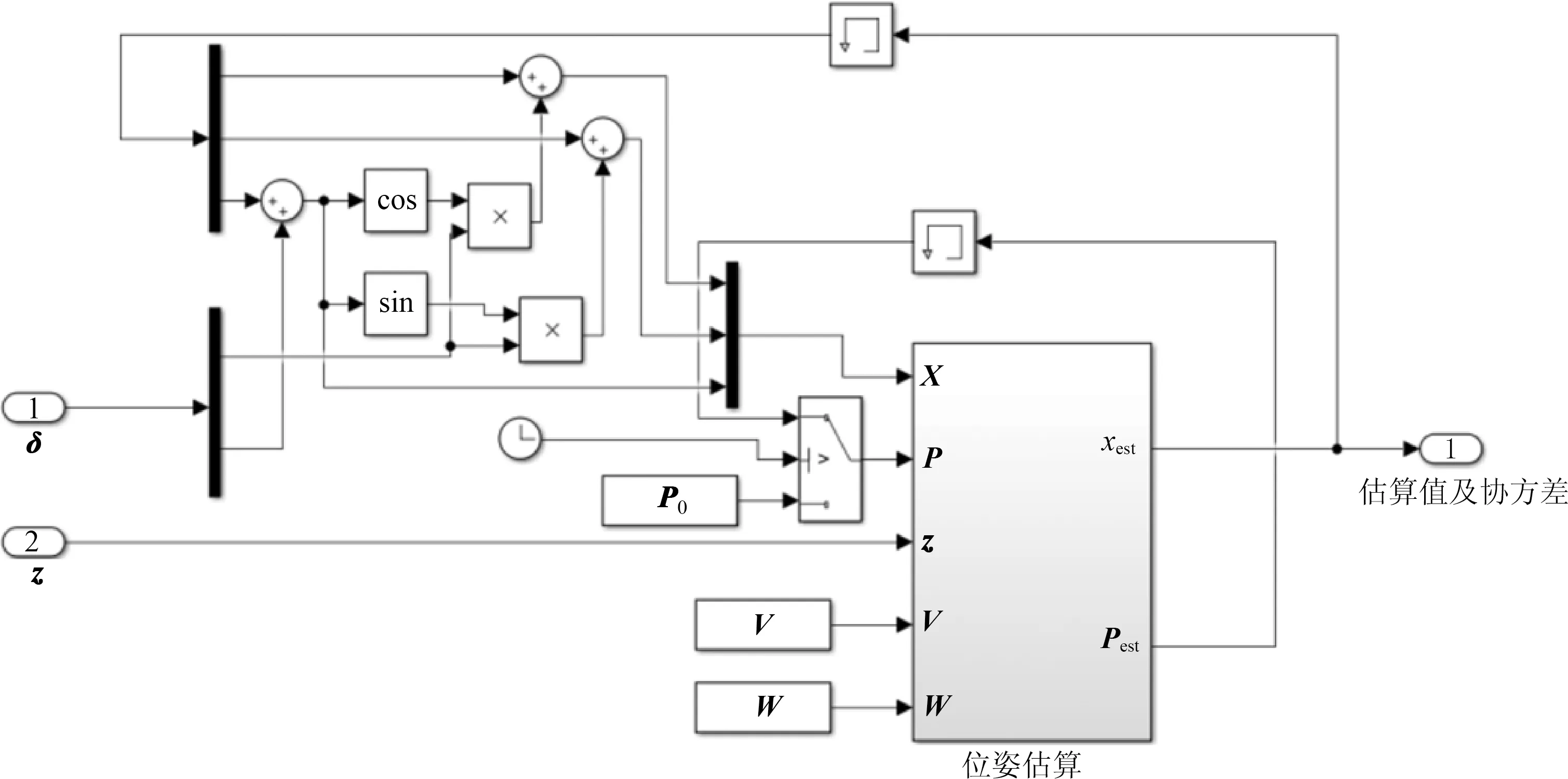
图8 信息融合位姿估算模型

3.5 仿真试验

车辆初始状态X0=(4.4,2.7,0)T，系统初始协方差矩阵的值较小，取P0=diag(0.0052,0.0052,0.0012)，视觉传感器观测模型协方差矩阵W=diag(0.12,0.12)，车辆跟踪的三段式泊车轨迹由车速uv与前轮转角φ随时间t的变化表示，轨迹为

(34)

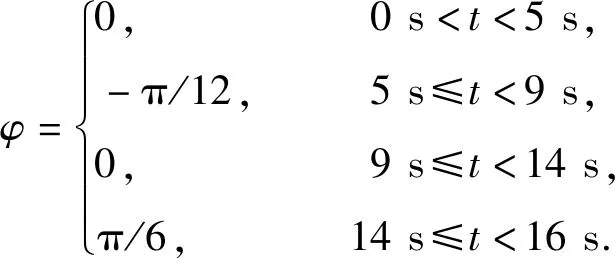
(35)

当传感器的测量方差V=diag(0.02,0.01)时，利用航迹推算方法的位姿估算与利用传感器信息融合的位姿估算结果进行对比，如图10所示.

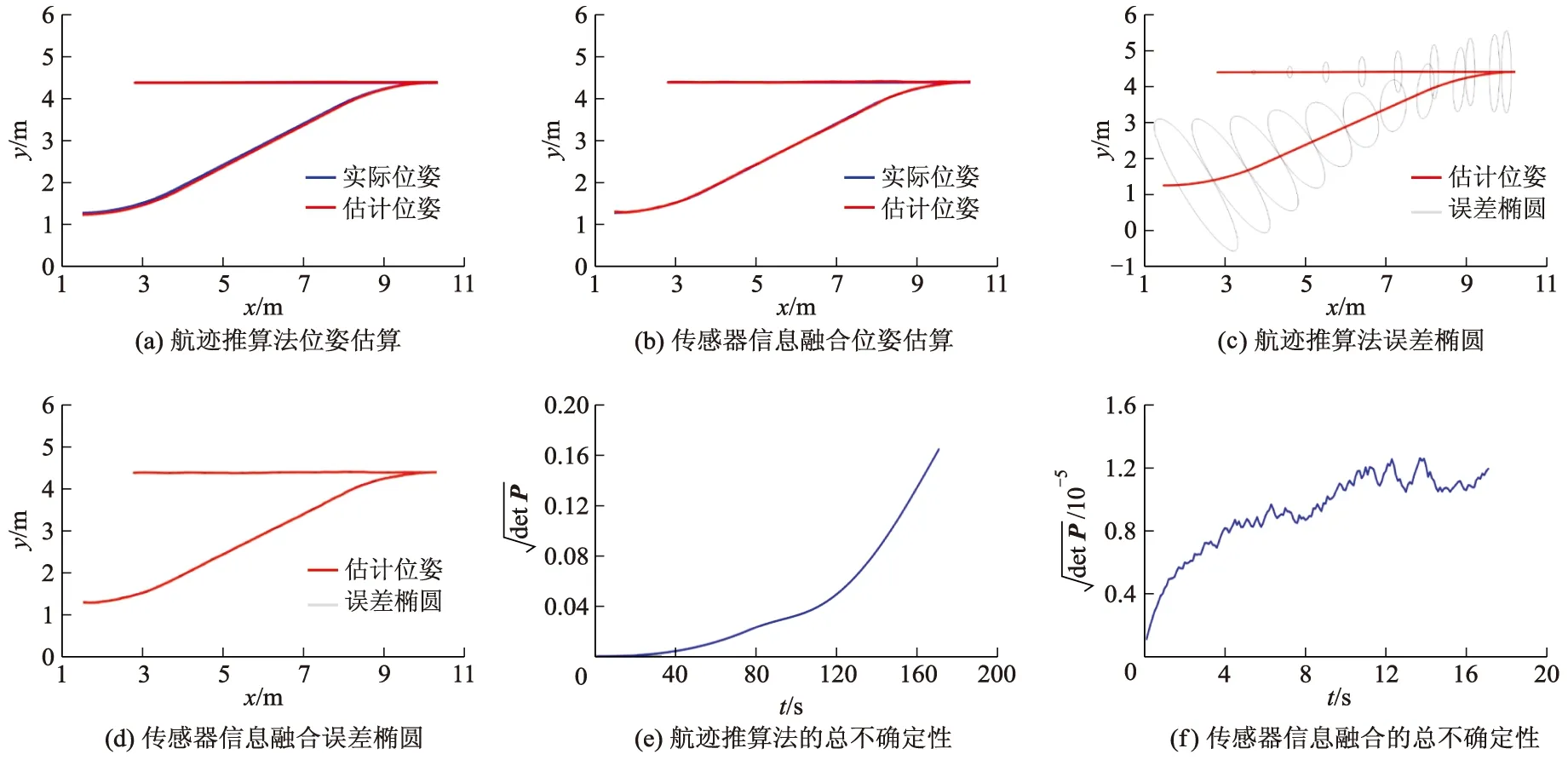
图9 V=diag(0.000 2,0.000 1)时的仿真试验结果对比

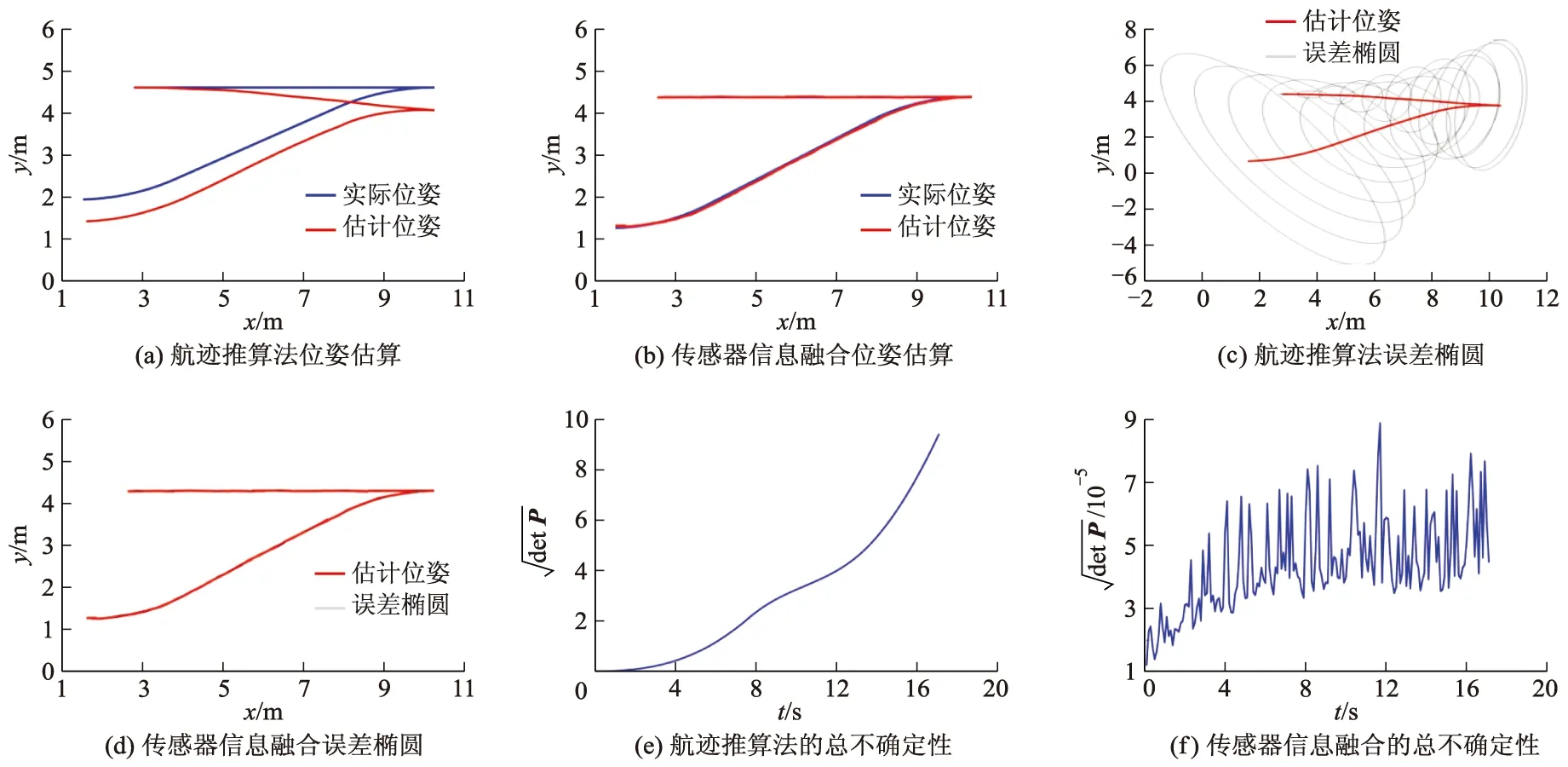
图10 V=diag(0.02,0.01)时的仿真试验结果对比

基于上述2种仿真试验结果可以看出：在测量协方差较大时，提出的基于传感器信息融合的位姿估算精度明显优于航迹推算法.

4 结 论

针对自动泊车过程中车辆位姿确定的问题进行了研究，提出了一种基于扩展卡尔曼滤波算法融合轮速传感器信息与视觉传感器信息车辆位姿定位的估算方法，提高自动泊车过程的车辆位姿定位精度.首先研究了仅利用两后轮轮速传感器信息对车辆进行位姿估算的航迹推算法，分析了误差产生的原因；然后提出了基于轮速传感器与视觉传感器融合的车辆定位方法，通过扩展卡尔曼滤波算法将视觉传感器与轮速传感器信息进行融合，减小系统误差的同时实现自动泊车过程中的车辆位姿定位；最后使用Simulink建模仿真对算法进行验证，并将航迹推算法与传感器信息融合方法进行比较.结果表明：本研究的利用视觉传感器与轮速传感器进行信息融合的车辆位姿估算方法能够有效降低系统定位误差，提高泊车过程中车辆位姿的估算精度.