P-CS 不确定性量化模型与其性能数据驱动更新方法1)

何佳琦 贾晓璇 吴伟达 钟杰华 罗阳军,2)

* (大连理工大学航空航天学院,辽宁大连 116024)

†(中国运载火箭研究院,北京 100076)

引言

实际工程问题往往包含多源不确定性变量,如荷载、结构自身材料属性(杨氏模量、磁导率等)、结构服役环境(磁场、温度场等)、结构加工误差以及传感器测试误差等.这些不确定性信息直接或间接影响着工程结构形式设计[1]、结构性能评估与预测[2]以及在役结构损伤识别[3]等工作的开展与决策.建立合适的数学模型来量化这些不确定性变量是开展考虑上述不确定性的结构分析与设计工作的前提与基础.

传统处理不确定性变量的方法通常将其量化为概率统计变量[4-6],但概率模型只适用于先验信息充足且测试样本容量足够大的客观不确定性.对于无充足先验知识、仅具有少量数据样本的客观或主观不确定性变量,Ben-Hahn[7-8]在20 世纪90 年代放弃传统概率理论框架,提出了用凸集模型描述变量不确定性的非概率思想.近年来,大量学者针对非概率模型的建立与结构性能非概率测度描述方法做了一系列的研究工作[9-12].

对于具备有限先验知识与有限数据样本的情况,一些学者还结合区间理论提出了非精确概率不确定性量化方法,核心思想是用一个概率的区间模型取代精确概率值来表现由于先验知识与数据样本不充足而引入的主观不确定性,并形成了一系列相关方法论,主要包括DS 证据理论[13-14]、P-Boxes 模型[15-16]与模糊概率模型(fuzzy probabilities)[17-18].其中,DS 证据理论基于信任函数和似然函数给出上限概率与下限概率,为不确定性量化尤其是多源不确定信息融合提供了合理且较为完备的理论框架,已广泛应用于多传感器监测信息融合[19]、失效模式分析[20]、结构可靠性评估[21]等领域.P-Boxes 模型本质上是通过求解一系列优化问题寻找到非精确概率不确定性变量的边界概率密度累积函数,进而用这些边界概率密度累积函数界定变量的不确定性范围.目前,已有一些学者利用P-Boxes 模型开展多源不确定性量化分析[22]、结构剩余寿命评估[23],以及考虑不确定性的侵入式结构有限元分析[24]等问题的研究.模糊概率模型是模糊集理论与概率模型的结合,随机不确定性由概率模型描述,而概率模型的不精确性由模糊集隶属度函数(membership function)[25-26]描述.目前已有一些学者基于模糊概率模型提出了结构可靠性评估方法[18,25-29]与疲劳强度分析方法[30].考虑到结构在服役期间,不确定性因素会随时间变化,一些学者针对时变不确定性问题开展了研究.Li 等[31]基于P-Box 模型提出了一种用于量化时变不确定性的非精确随机过程模型;Ping 等[32]基于正交级数展开、稀疏网格数值积分以及混沌多项式展开等数值方法提出了对于非高斯随机过程的不确定性传播算法;考虑到时变不确定性的结构失效概率在一个时间段为一区间值,Wang等[33]提出了一种非概率区间过程模型,Meng 等[34]结合概率模型(量化随机不确定性变量)与凸集模型(量化功能函数在某一时间段的变化范围)提出了一种求解时变可靠性指标的迭代算法;为避免因大规模求解功能函数而造成时间成本过高的问题,一些学者结合Kriging 代理模型提出了效率较高的失效概率区间计算方法[35-36].

尽管上述各类模型与算法根据各自的适用范围已广泛应用于不同领域各类问题中,然而,多源不确定性量化依旧存在下述两个问题难以兼顾解决:(1)实际工程问题往往既包含可用概率模型量化的不确定性变量,也包含适用于非概率模型量化的不确定性变量,两者之间存在复杂层级关系;(2)一些不确定性变量在使用过程中随时间变化,且在使用过程中难以直接测量,需要根据间接性能测试信息在使用工程中更新不确定性量化模型.这些不确定性变量既包括随时间变化的客观不确定性变量如环境载荷(冰、雪、风、波浪等)、结构本身属性(杨氏模量、屈服强度、阻尼系数等),也包括随着更多相关信息加入而不确定性逐步减小的主观不确定性变量.对于问题(1),尽管P-Boxes 模型可融合概率不确定性变量与非概率不确定性变量,但由于该模型求解较为复杂,很难基于P-Boxes 模型进行基于性能测试数据驱动的量化更新计算.对于问题(2),一些学者基于贝叶斯理论[37]与证据合成理论[38]分别针对概率模型[39]与非概率模型[40]提出了更新算法.但考虑到兼顾问题(1)与问题(2),目前尚没有能统一描述多源不确定性且易于性能数据驱动更新的不确定性量化模型.

本文为兼顾解决上述问题,提出一种P-CS(probability-convex set)不确定性量化模型,用以实现多源、多类型不确定性的统一量化以及性能测试数据驱动模型的更新计算.基于该模型,可将概率模型、非概率模型以及非精确概率模型在同一框架下统一表达,本文将分别用一维、二维与三维P-CS 模型详细展示P-CS 模型的构建过程并讨论其概率与非概率特性.进而,基于贝叶斯理论提出P-CS 模型参数在性能数据测试样本驱动下的更新算法,并分别采用悬臂梁结构与框架结构算例来展示更新计算过程并验证算法的适用性.

1 P-CS 不确定性量化模型

1.1 P-CS 不确定性量化模型表达形式

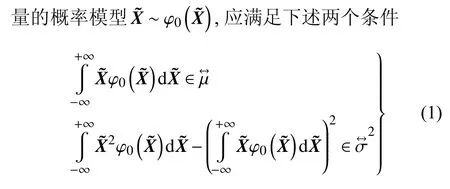
当给定随机变量的概率模型后,凸集模型Ω用来表征: 在某一概率水平 α 下,一簇概率模型的随机变量分位数Xα相对于随机变量的分位数的变化范围.P-CS 模型可定义如下

1.2 一维P-CS 模型构建方法

由表1 可知,只有针对“已知变量可能的概率分布形式,概率参数不确定但有界”的非精确客观不确定性变量,P-CS 模型的构建区别于传统的概率模型与非概率模型.对于这种情况,其概率分布为一族函数,如图1 所示.

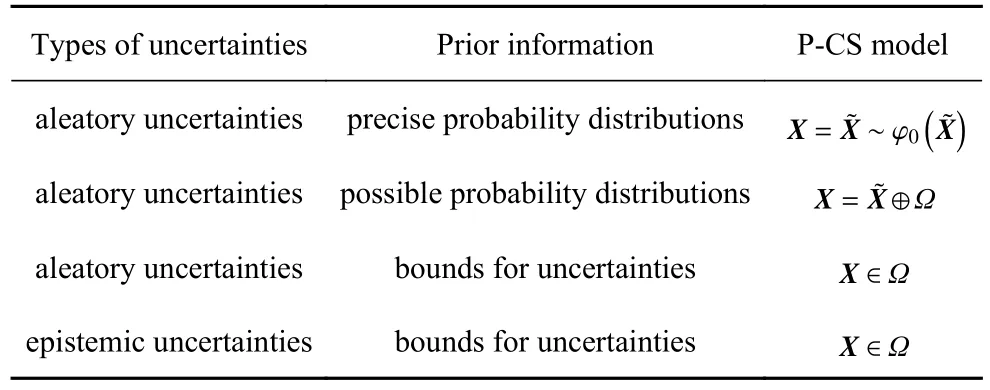
表1 多源不确定性变量的P-CS 量化模型Table 1 P-CS models for multi-source uncertainty

图1 非精确概率模型示意图Fig.1 Schematic illustration of imprecise probabilistic model

式(3)中,Xα关于变量 μ与 σ 为线性变化,因此

1.3 多维P-CS 模型构建方法

由此,无量纲椭球模型可表达为

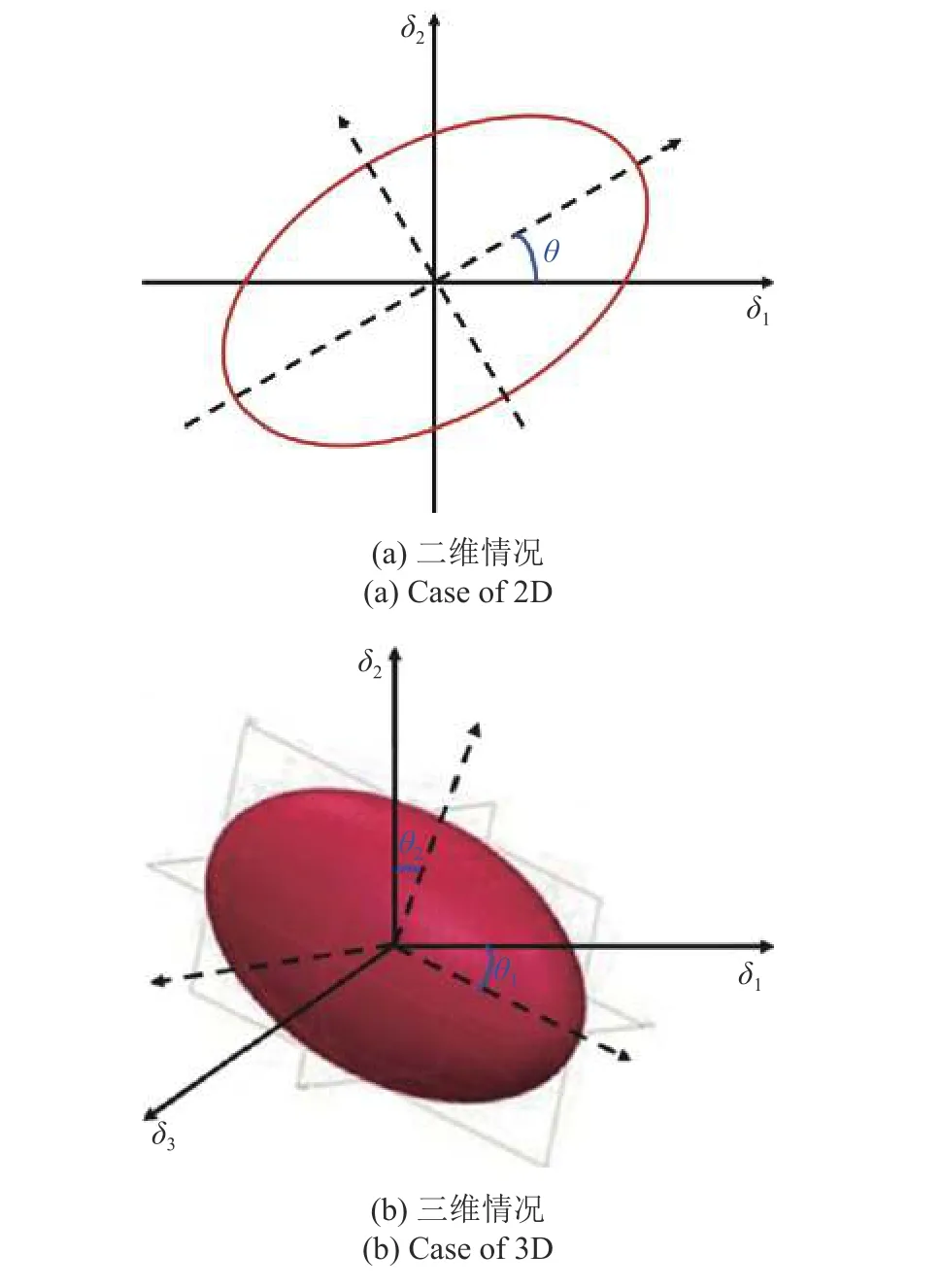
图2 椭球模型旋转角度示意图Fig.2 Schematic illustration of the rotation angle of ellipsoidal model

在实际工程中,对于非精确概率变量很难给出清晰的不确定性变量之间的相关性关系,一般只能凭借工程经验判断变量之间是否相关.因此,本文将非概率椭球模型中关于变量间的相关性进行模糊处理.考虑到随着后续测试样本的输入,可逐步降低变量间相关性的模糊程度,使非概率多椭球模型逐渐变得精确.故而,初始多椭球模型可构建为包络超立方盒模型 Ωcubic的最小体积超椭球模型.在几何学上,可包络Ni维区间模型的最小椭球,其主轴方向 θ0沿区间长度最大的维度,其第k维度半轴长与变化范围区间长度dk=存在下述对应关系式

2 性能测试信息驱动的P-CS 不确定性量化模型更新算法

结构在服役过程中往往会产生新的测试数据,这些新的测试数据的加入使得主观不确定性减小,不确定变量之间非概率相关性模糊程度降低,表现为P-CS 模型中表征不确定性范围的多椭球凸集模型体积减小与椭球方向角的改变.实时性能测试数据驱动P-CS 模型更新就是根据实时性能测试数据对P-CS 模型中表征不确定性范围的多椭球凸集模型参数进行更新计算,本质上就是在计及实时性能测试数据的基础上寻求当前最可能的参数值组合.为了寻求可能性最大的参数值组合,这里把参数值的可能性用参数“信度”这一概念加以量化.

对标准化参数取值范围做m个划分Ai(i=1,2,···,m),Ai满足如式(13)所列出的条件,将X落入Ai的概率定义为信度,记为Pl(X∈Ai)或简略为Pl(Ai) .

图3 二维焦元示意图Fig.3 Schematic illustration of 2-dimensional focus elements

多个焦元Bi,i=1,2,···,n的并集的信度等于每个焦元信度的和,即

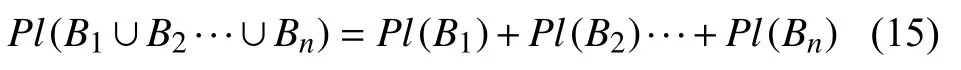
2.1 似然信度定义

其中,fPDF(·) 为标准正态分布概率密度函数,τi表示第i个多维椭球模型参数.

2.2 基于贝叶斯理论更新P-CS 模型

考虑到基于不同多椭球按照优化列式(17)计算得到的性能可能取值范围会存在重叠现象.而根据式(16)的定义,当一个样本值落入到重叠部分,不同的焦元会获得相同的似然信度.不同焦元对应的多椭球模型体积不同,显然基于体积越大的多椭球模型可获得范围更大的性能取值域.因此,在式(16)对似然信度定义的基础上,对多椭球模型的体积进行了“惩罚”,即定义焦元对应的多椭球模型体积与焦元似然信度成反比例,在P-CS 模型更新过程中,对于给定P-CS 模型 C(m),测试样本为 ν=ν0的似然信度可进一步定义为

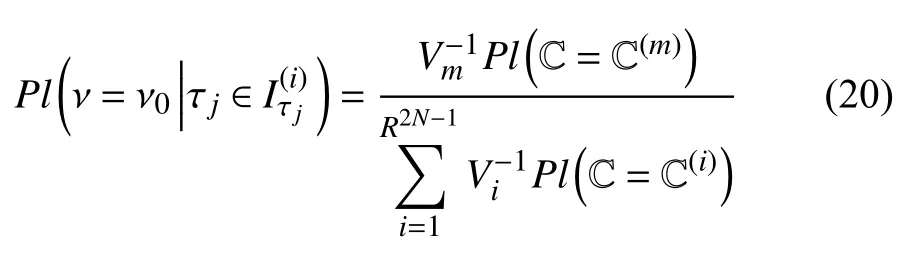
其中,Vm为P-CS 模型 C(m)中多椭球模型体积.

基于贝叶斯方法,可根据性能测试样本数据更新多椭球模型参数取值划分的信度.对于第j个参数 τj,其信度更新贝叶斯公式如下

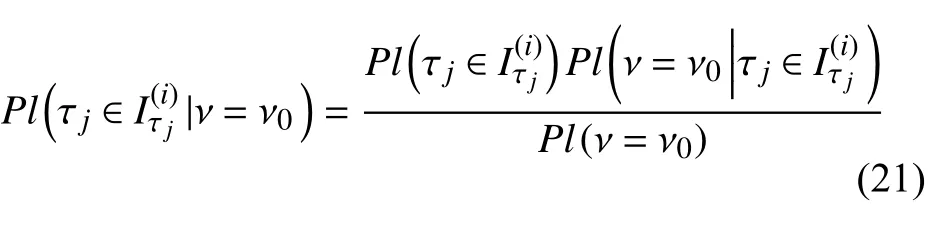
其中,Pl(ν=ν0) 表示参数τj取任意值,测试样本为ν=ν0的似然信度,根据式(15),信度具有可加性,所以

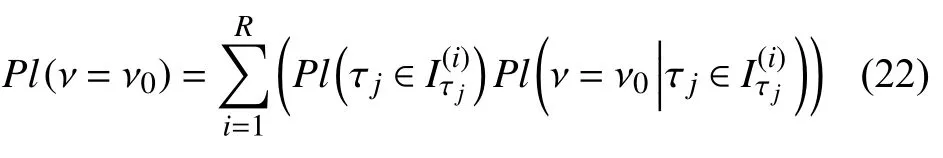
对无初始信度信息的问题,参数先验信度可定义为每一个焦元等信度,即

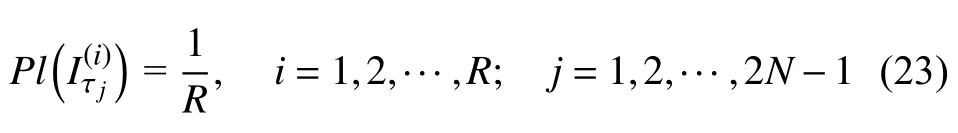
在更新计算过程中,可按下式计算更新后椭球模型参数的参数值,即

2.3 更新算法流程

考虑到焦元数量M=R2N-1,为提高计算效率,本文采取一种根据参数后验信度分布,逐渐减小参数值取值范围的多次数更新策略.在读入样本数据后,更新算法流程图如图4 所示,具体步骤详述如下.

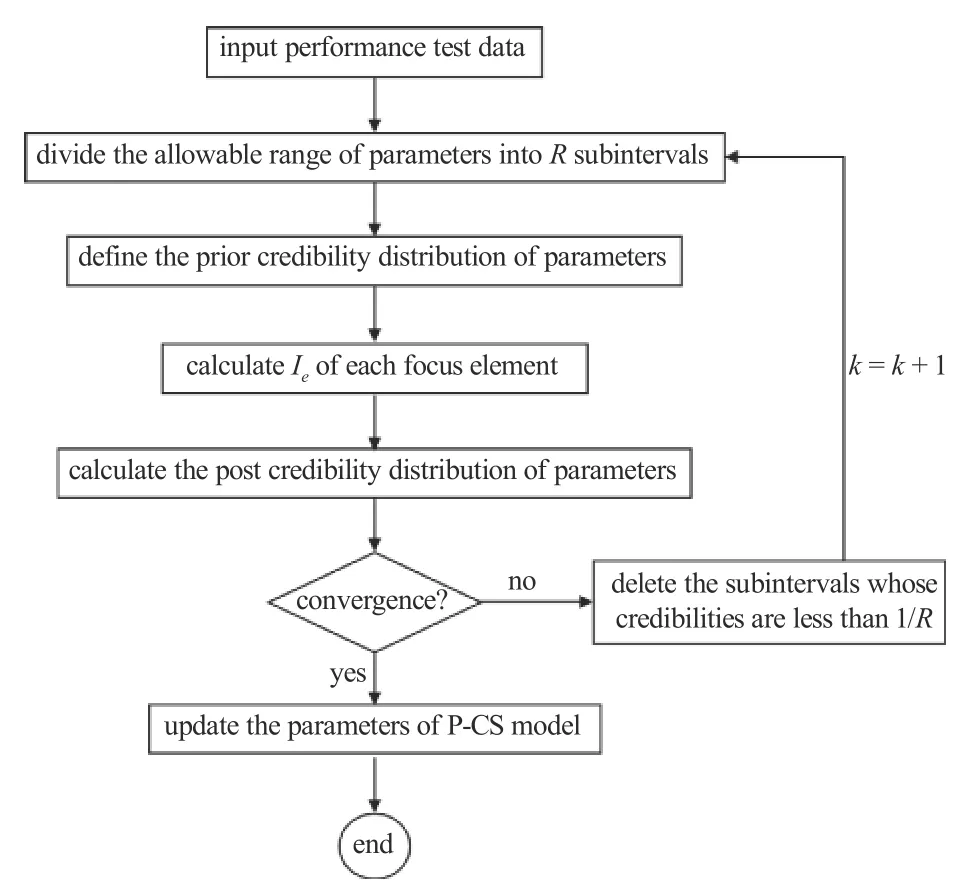
图4 更新计算方法流程图Fig.4 A flow chart of the updating method

步骤1:根据式(18)确定各初始参数取值范围,并分别将各初始参数取值范围做R个划分,建议R≤6,并根据式(23)定义初始先验信度分布,根据式(17)计算每一个焦元对应的性能函数值的期望变化范围Ie,进而根据式(21)做第k=1 次更新计算,得出参数后验分布.

步骤2:若在第k次更新计算后,第j个参数的第i个划分的后验信度则在参数取值范围中将区间去掉,得到取值范围

步骤3:将取值范围做R个划分,并根据式(23)定义初始先验信度分布,根据式(17)计算每一个焦元对应的性能函数值的期望变化范围Ie,进而根据式(21)做更新计算,得出参数后验分布.

步骤4:重复步骤2 与步骤3,直至在第K次更新计算中,每一个参数的划分区间都足够小,则终止多次更新计算.可定义多次更新计算终止条件为

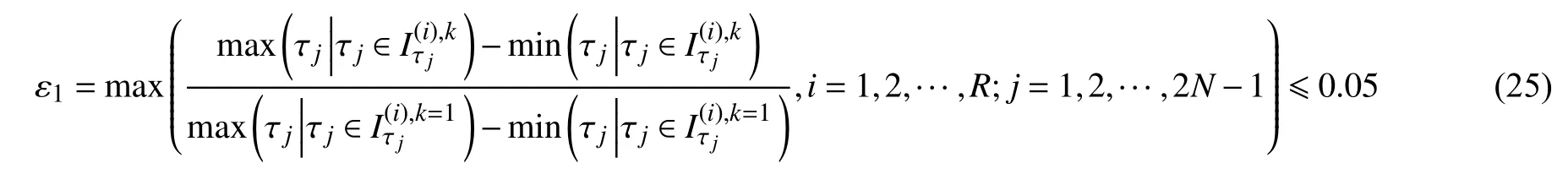
考虑到可能会出现某一参数在其取值区间内变化对结构性能影响很小的情况,会使该参数在该取值区间内的每个划分的后验信度近似相等,在 1/R附近以较小的幅值波动,即可理解为该参数在该取值区间内可以取任意值.对于上述情况的出现,可终止对该参数的进一步更新计算,可将该取值区间的中心点值作为该参数本次更新计算的结果,并在第k=k+1次更新计算中不再改变该参数的取值.因此,可定义第j个参数的多次更新终止条件

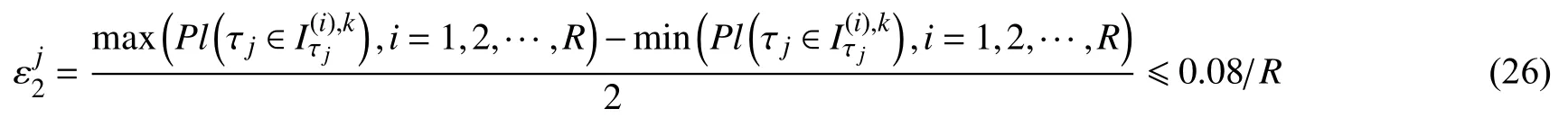
步骤5:在多次更新计算终止后,根据式(24)逐次倒序计算参数取值.若步骤3 中共进行K次更新计算,即

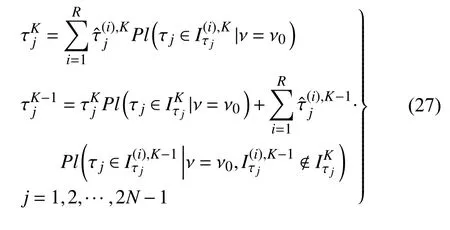
3 数值算例

3.1 P-CS 量化模型构建

3.1.1 一维不确定性变量算例

假定待量化的某不确定性变量描述为X～Nμ ∈[3.5,4.5],σ2∈[0.5,1.5] .该不确定性变量本质上可量化为一族无限个精确概率模型的组合.取该族内8 个概率密度累积函数可绘制成图5.

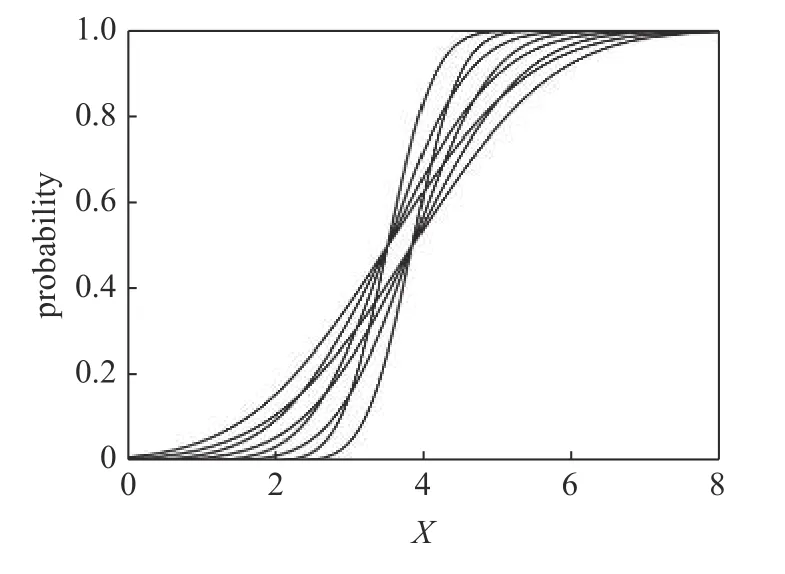
图5 概率密度累积函数族Fig.5 Family of probability density cumulative functions

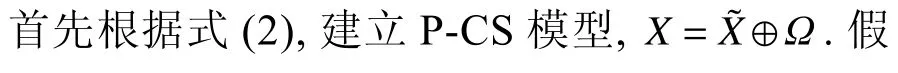
概率密度累积函数族的边界分别由四个正态分布概率密度累积函数构成,分别为X～N(4.5,1.5),X～N(4.5,0.5),X～N(3.5,1.5),X～N(3.5,0.5),如图6 所示.

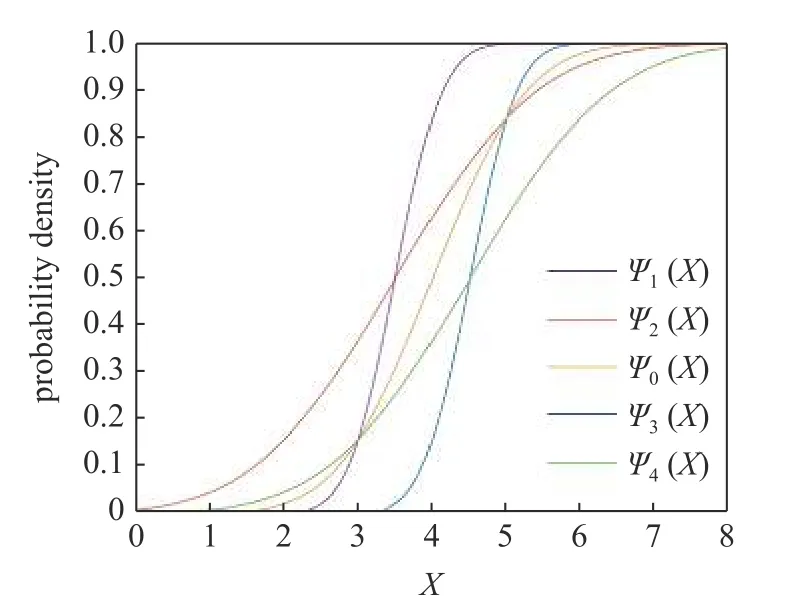
图6 概率密度累积函数族的边界Fig.6 Boundaries for the family of probability density cumulative functions

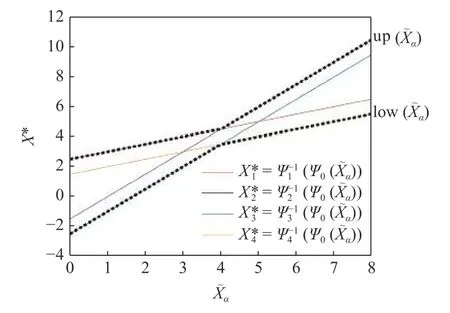
图7 等概率水平条件下不确定性变量变化范围验证Fig.7 Validation of the variation range of uncertainties under equal probability levels

3.1.2 二维不确定性变量算例

对于给定某一概率水平 α,即可根据式(30)～式(33)分别计算Xα相对于的变化范围 Ω .考虑到本算例变量间存在相关性,可以用一个最小体积的椭圆模型将在某一概率水平 α下Xα的所有可能取值包络.选取2 个随机变量分位数=(4,3) 与=(3,2.6),可得出在该随机变量分位数处,由等概率原则得到的非概率椭圆凸集模型范围,如图8 所示.

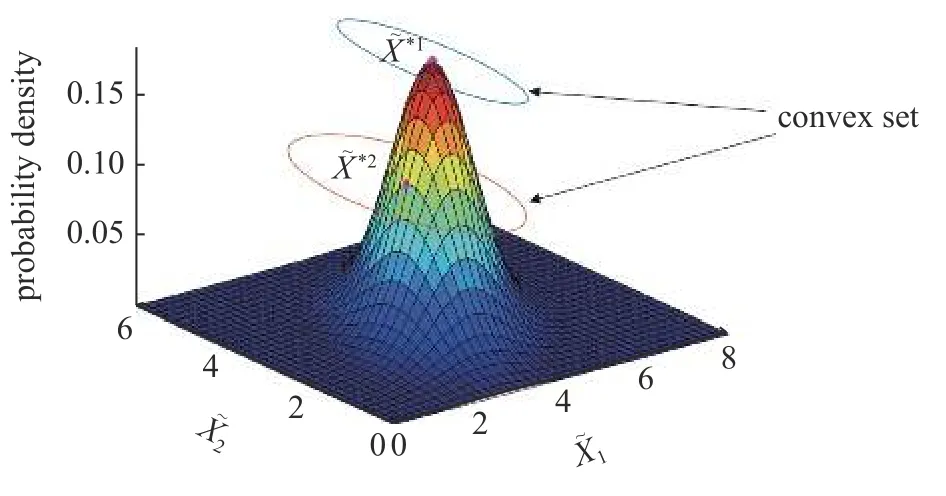
图8 二维 P-CS 模型示意图Fig.8 Schematic illustration of the 2D P-CS model

为验证与讨论椭圆模型对上述一簇概率随机变量分位数的包络性,在本问题的概率密度函数族中选取16 组边界概率密度函数(μ1,σ1,μ2,σ2分别取最大值与最小值进行排列组合),并分别计算出与随机变量分位数与等概率水平下的其他16 组概率密度函数对应的分位数.如图9 所示,椭圆中心点为随机变量分位数与.对于同等概率水平下的,其16 个点(图9(a)中每个角点包含4 个位置重复的点)皆位于椭圆模型边界上;对于同等概率水平下的,其12 个点位于椭圆模型内,4 个角点皆位于椭圆模型边界上.因此,可以验证由本文提出的凸集构建方法可构造出包络等概率水平下一簇随机变量分位数的最小椭圆模型.3 维及3 维以上多维椭球模型与二维椭圆模型情况完全类似,不再多加讨论.

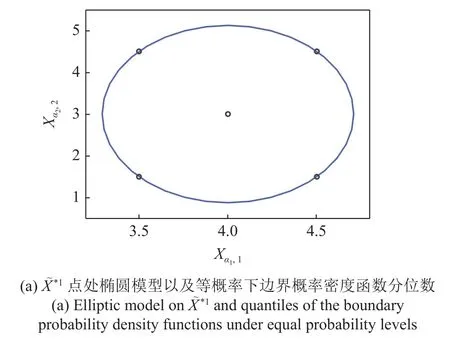
图9 等概率水平下椭圆模型包络性验证Fig.9 Validation of elliptic model envelope under equal probability levels

3.1.3 多源不确定性输入构建P-CS 模型

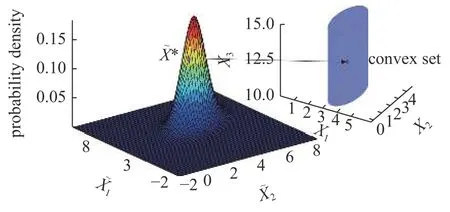
图10 多源不确定性P-CS 模型示意图Fig.10 Schematic illustration of the multidimensional P-CS model

3.2 悬臂梁结构算例

本算例为一悬臂梁算例,其结构形式如图11 所示,悬臂梁长度为L=1 m,横截面惯性矩为I=1×10-4m4,材料弹性模量为E=100 GPa .结构承受集中载荷P1与均布载(荷P2.)集中载荷与均布载荷存在不确定性,P1～,μ1∈[3.5,4.5]kN,σ1=1 kN,P2∈[1.5,2.5] kN/m.假定均布载荷P1与集中载荷P2之间存在相关性,性能测试信息为梁端处转角位移 β,具体样本数值统计为表2.由于本文算例为验证算法合理性,故文中性能测试样本皆为数值模拟计算产生,非试验测试值.

表2 悬臂梁结构算例性能测试样本Table 2 Performance test samples of the example of a cantilevered beam structure10-4/rad

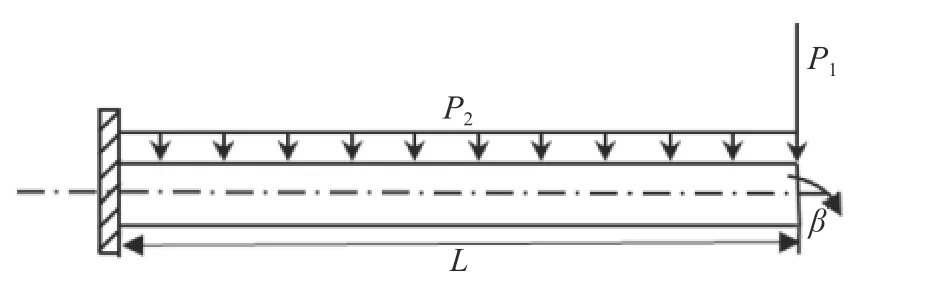
图11 悬臂梁结构Fig.11 A cantilevered beam structure

根据结构力学原理,可推导出悬臂梁端转角β与载荷之间的数学表达关系式为

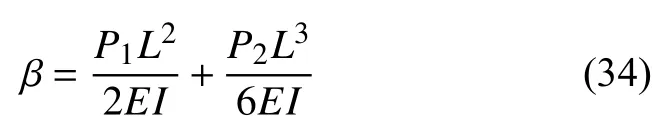
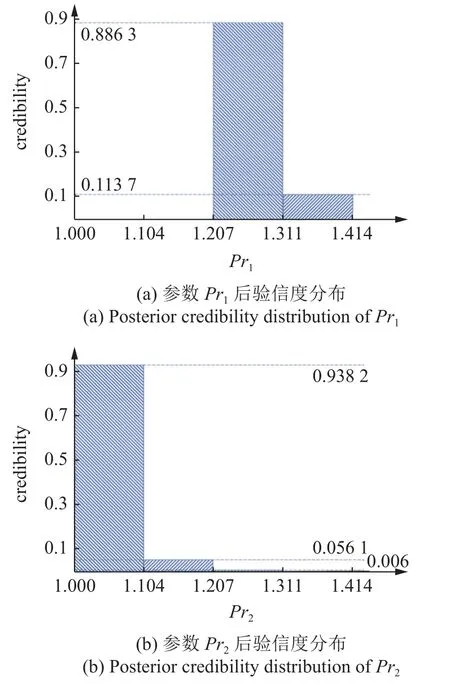
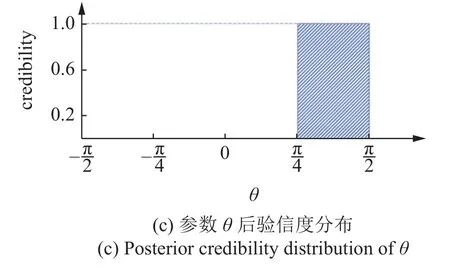
图12 第1 次更新计算后参数后验信度分布Fig.12 Posterior credibility distributions after the first updating

根据第一次更新后的信度分布情况,选取下一次更新的参数取值范围为Pr1∈[1.207,1.311],Pr2∈[1,1.104],θ∈[π/4,π/2] .将上述取值范围分别做4 个划分,形成64 个焦元.在第二次更新计算后,参数后验信度如图13 所示.

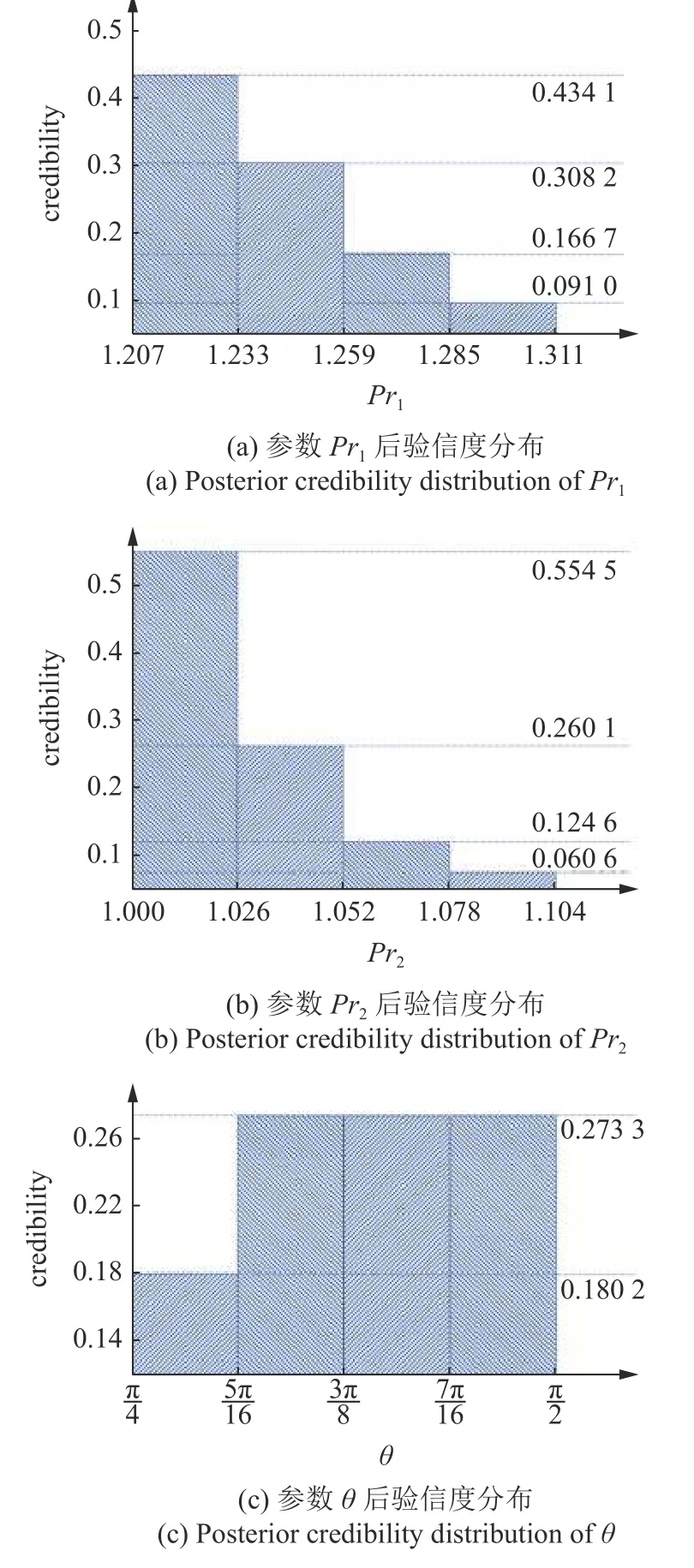
图13 第2 次更新计算后参数后验信度分布Fig.13 Posterior credibility distributions after the second updating

根据第二次更新后的信度分布情况,选取下一次更新的参数取值范围为Pr1∈[1.207,1.259],Pr2∈[1,1.052],θ∈[5π/16,π/2] .将上述取值范围分别做4 个划分,形成64 个焦元.在第三次更新计算后,参数后验信度如图14 所示.

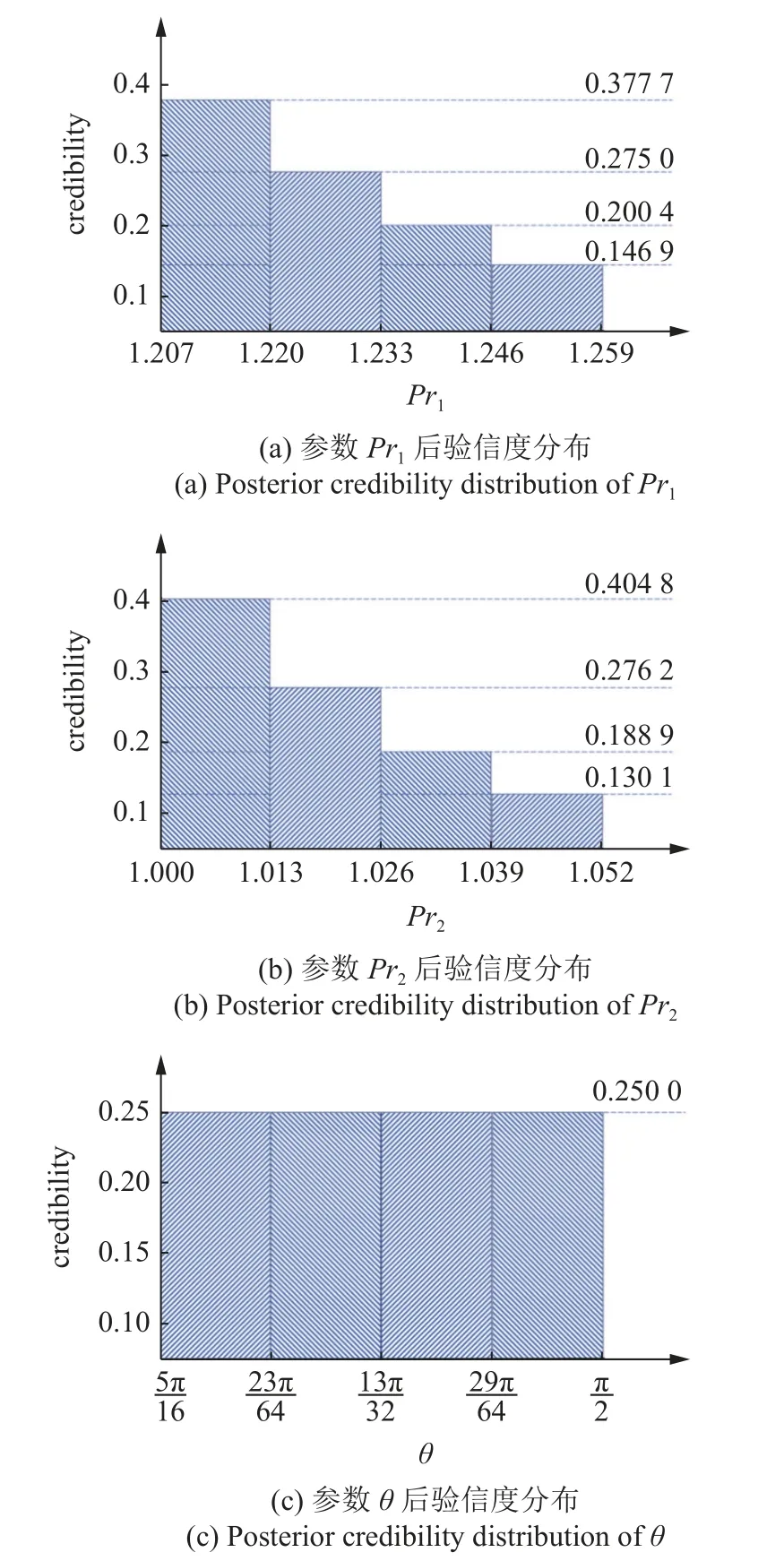
图14 第3 次更新计算后参数后验信度分布Fig.14 Posterior credibility distributions after the third updating

共进行了3 次更新计算后,对于参数 θ,根据式(26),=0,对于参数Pr1与Pr2,根据式(25),ε1=0.03 ＜0.05,满足了多次更新终止条件.3 次更新计算共形成了192 个焦元,最终信度分布如图15 所示,最终参数取值根据式(27) 计算为Pr1=1.239,Pr2=1.038,θ=1.205 .为验证本文焦元选取策略的准确性,对初始参数取值范围分别做40 个划分,形成64 000 个焦元,经一次更新计算后根据式(24)计算得到参数取值为Pr1=1.232,Pr2=1.037,θ=0.996 .对于参数Pr1与Pr2,计算误差分别为0.6%与0.1%.对于参数 θ,由其后验分布可以看出,当θ ∈[5π/16,π/2]时,其参数真实值落在每一个划分的信度均等,即参数可以取为该范围内任何值.由此可见,本文提供的焦元选取策略可以在较少焦元计算量的基础上获得较高的计算精度.

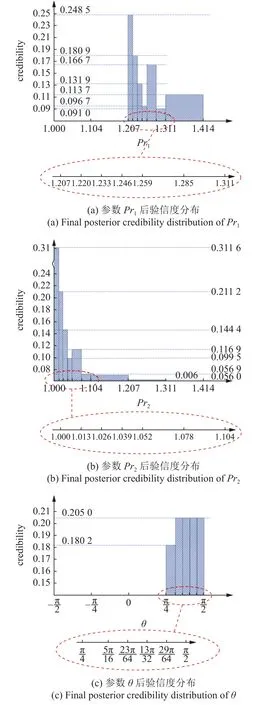
图15 悬臂梁结构算例最终参数后验信度分布Fig.15 Final posterior credibility distributions of the example of a cantilevered beam structure

在更新过程中,每一个新的样本点输入后皆按2.3 节所述的多次更新策略更新参数划分的后验信度,进而根据式(27)计算得出当前的P-CS 模型参数.在得到更新后的模型参数后,可根据优化列式(17)计算出当前梁端转角上限βup与下限βlow,其变化趋势与均值点处椭圆凸集模型变化如图16所示.

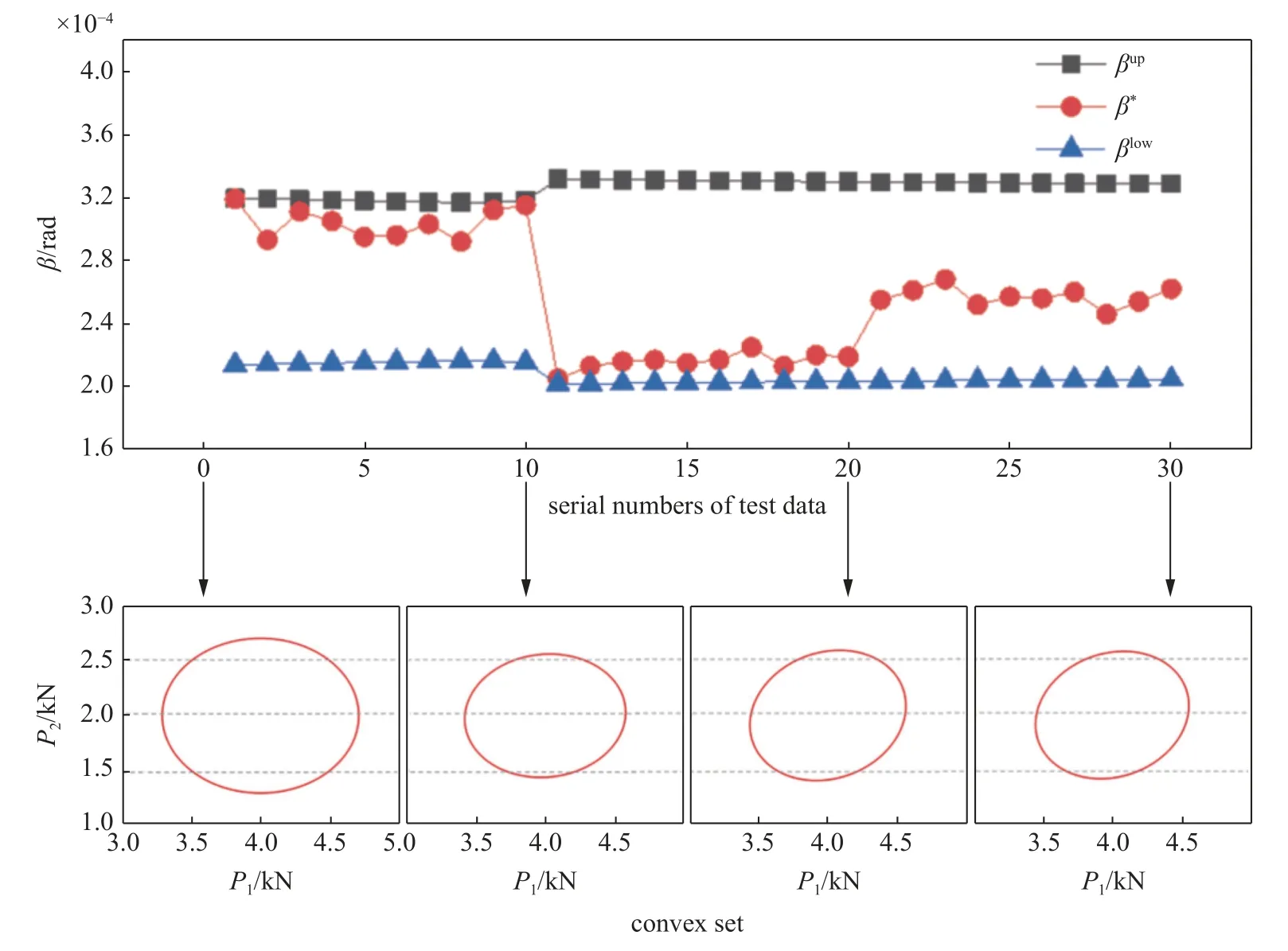
图16 悬臂梁结构算例更新过程图Fig.16 The updating process of the example of a cantilevered beam structure

从图16 中可以看出,样本测试值一直处于基于当前P-CS 模型的梁端转角上限与下限范围内.前10 个性能测试样本点变化范围较小,表示不确定性变量波动范围较小,P-CS 模型中表征不确定性范围的椭圆模型逐步变小,同时梁端转角上限与下限范围也在缩小.当第11 个性能测试样本点输入后,该次采样点较之前采样点数值变化很大,这说明不确定性变量从第11 个点开始波动到了另一个范围,该范围显然不在当前P-CS 模型的不确定性范围内,所以P-CS 中表征不确定性范围的椭圆模型变大,同时梁端转角上限与下限范围也在变大.而后续采样点较第11 个采样点变化较小,所以椭圆模型变小同时梁端转角范围也在变小.当第21 个性能测试样本点输入后,该次采样点较第11 至第20 采样点数值变化很大,这说明不确定性变量从第21 个点开始波动到了另一个范围,而新的变化范围仍在当前P-CS 模型范围内,因此P-CS 模型中表征不确定性范围的椭圆模型继续变小,同时梁端转角上限与下限范围也在继续变小.

3.3 框架结构算例

本算例为一框架结构,如图17 所示.该结构由3 根梁构成,两个梁之间为刚性连接,2 号梁与 3 号梁在3 号节点与4 号节点施加固支约束.1 号梁的长度L1=1.44 m,2 号梁与3 号梁的长度L2=L3=0.96 m.3 根梁的横截面相同,皆为边长为 0.1 m 的正方形.结构承受垂直方向的均布载荷P1与水平方向局部载荷P2,P3,其中水平方向的均布载荷P2与P3大小相等,方向相反.不确定性变量包括: 横向梁(1号梁)材料弹(性模量)E1,E1∈[29,31] GPa(,载荷不)确定性P1～,P23=P2=P3～μ1=μ2∈[36,44] kN,σ1=σ2=2 kN,载荷不确定性变量P1与P23相关.2 号梁与3 号梁的材料弹性模量分别为E2=E3=30 GPa .性能测试信息为角点1 处转角位移 β,具体样本数值统计为表3.由于本文算例为验证算法合理性,故文中性能测试样本皆为数值模拟计算产生,非试验测试值.可基于有限元方法建立2 号角点转角位移 β 与不确定变量之间的数学关系,即β=g(X) .

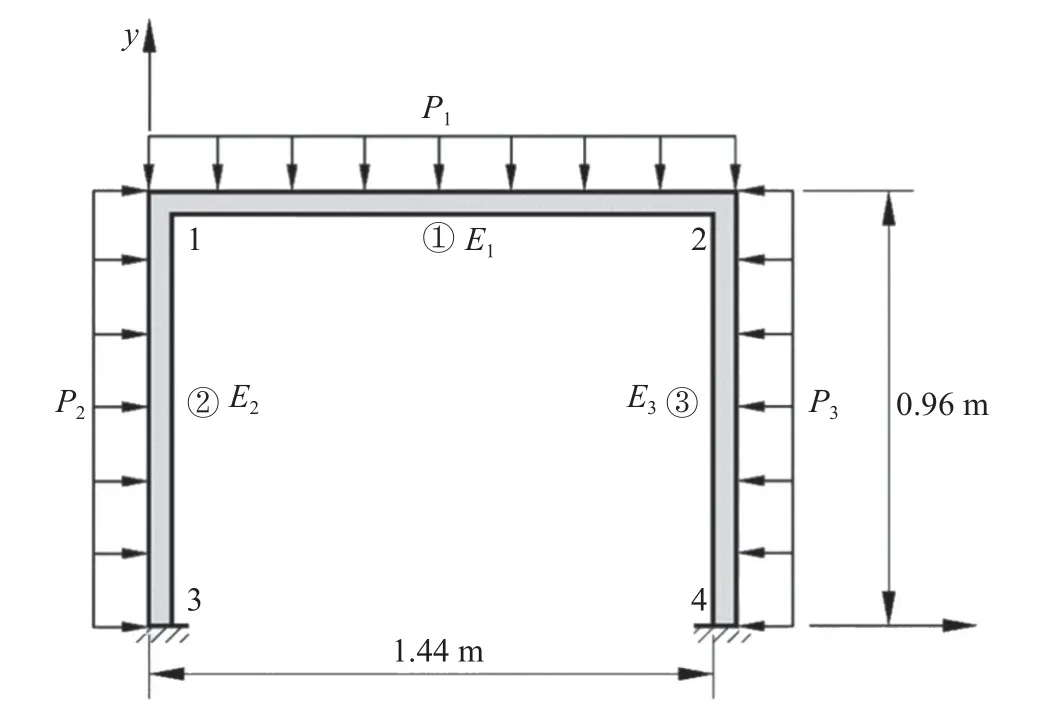
图17 框架结构Fig.17 A frame structure

表3 框架结构算例性能测试样本(10-4/rad)Table 3 Performance test samples of the example of a frame structure (10-4/rad)

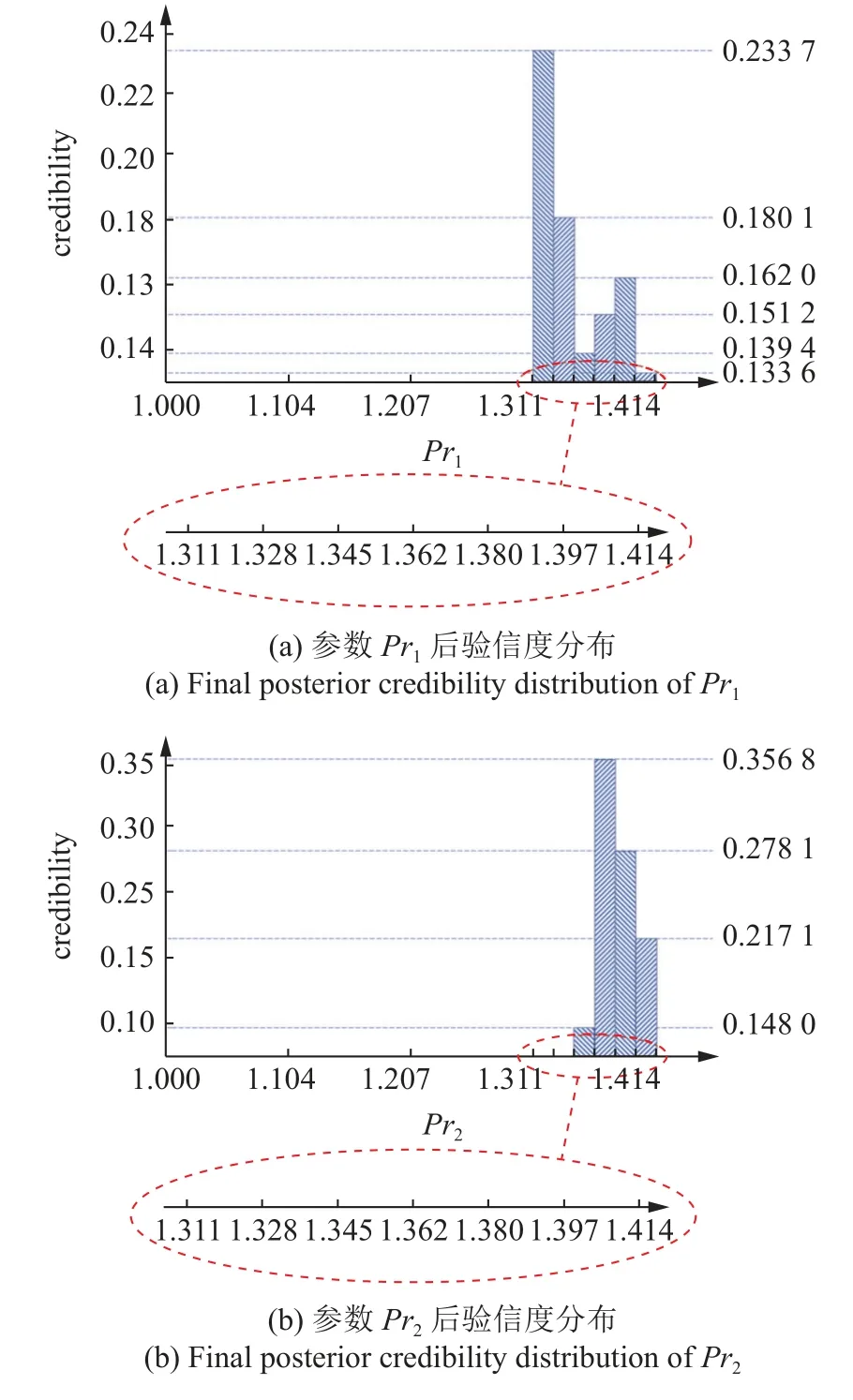
图18 框架结构算例最终参数后验信度分布Fig.18 Final posterior credibility distributions of the example of a frame structure

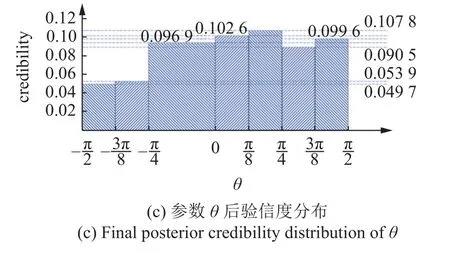
图18 框架结构算例最终参数后验信度分布(续)Fig.18 Final posterior credibility distributions of the example of a frame structure (continued)

随着性能测试信息 β*输入,每一个新的样本点输入后皆按3.3 节所述的多次更新策略更新参数划分的后验信度,进而根据式(27) 计算得出当前的P-CS 模型参数.在得到更新后的模型参数后,可根据优化列式(17)计算出当前转角位移的上限 βup与下限βlow,其变化趋势与均值点处多椭球凸集模型变化如图19 所示.

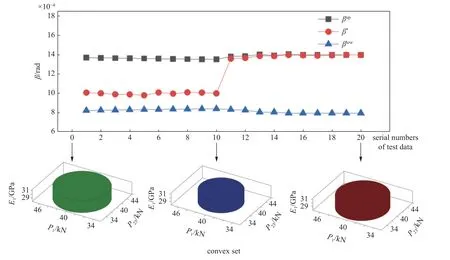
图19 框架结构算例更新过程图Fig.19 The updating process of the example of a frame structure

从图19 中可以看出,样本测试值一直处于基于当前P-CS 模型的转角位移上限与下限范围内.前10 个性能测试样本点变化范围较小,表示不确定性变量波动范围较小,P-CS 模型中表征不确定性范围的椭圆模型逐步变小,同时转角位移上限与下限范围也在缩小.当第11 个性能测试样本点输入后,该次采样点较之前采样点数值变化很大,而后续采样点较第11 个采样点变化较小,这说明不确定性变量从第11 个点开始波动到了另一个范围,因此P-CS模型中表征不确定性范围的椭圆模型变大,同时转角位移上限与下限范围也在变大.

4 结论

本文提出的P-CS 不确定性量化模型可以将概率随机变量、非概率凸集变量与非精确概率随机变量统一在一个模型框架下进行表征,从而实现对多源不确定性变量的统一模型量化.进而基于P-CS 模型,提出了一种性能测试信息驱动P-CS 模型参数更新的算法.

P-CS 不确定性量化模型由随机变量概率模型部分与多椭球非概率模型两部分组成,既具有概率特性也具有非概率特性.在给定某一概率水平的前提下,根据等概率原则可推导计算出在随机变量分位数,与其具有相同概率特性的不确定性变量取值范围.在数值算例1 中,本文详细阐述了一维、二维与三维P-CS 模型构建过程与其概率、非概率特性.

基于贝叶斯原理,提出了一种性能测试信息驱动P-CS 模型参数更新算法.采用参数信度概念取代传统贝叶斯理论框架内的条件概率进行更新计算,从而实现根据性能测试信息更新P-CS 模型参数的目的.数值算例中,本文分别提供了承受不确定性均布载荷与集中载荷的悬臂梁结构算例以及考虑材料属性与载荷不确定性耦合的框架结构算例,上述两个力学算例验证了本文提出的更新算法的适用性.

本文提出的P-CS 不确定性量化模型可解决多源、时变不确定性变量的量化与更新问题,并且该更新算法不需要在结构服役过程中对不确定性变量进行直接测量采样.该量化模型与其更新方法有着很强的实际工程应用价值,有望应用于考虑时变不确定性的结构形面、振动主动控制问题中.