一种面向激波噪声计算的加权优化紧致格式及非线性效应分析1)

李 虎 罗 勇 刘旭亮 武从海 韩帅斌 王益民

(中国空气动力研究与发展中心,空气动力学国家重点实验室,四川绵阳 621000)

(中国空气动力研究与发展中心,计算空气动力研究所,四川绵阳 621000)

引言

气动噪声是流体非定常运动引起的,主要有以下特征: 一是微尺度特性,近场声扰动的幅值比流体压力脉动的幅值小几个数量级[1-2];二是多尺度特性,湍流结构产生的噪声具有很宽的频率范围;三是声波近似等熵,无耗散和无色散,传播距离很远.气动噪声的微尺度、多尺度和近似等熵特性对数值模拟中的离散格式要求特别高,需要格式具有高阶精度以及宽频域的低耗散和低色散特性.

激波噪声是由流场中的湍流结构和激波的相互作用产生.因此,对于激波噪声问题,还要求数值格式具有鲁棒的激波捕捉能力.然而,同时捕捉激波和声波本质上是不相容的,因为前者的模拟需要消除激波周围的伪振荡波,而后者的模拟又需要准确分辨所有声波.到目前为止,还不存在适合于计算激波噪声的理想数值格式.为了实现激波噪声的精准模拟和预测,需要发展具有高阶精度、低色散、低耗散和鲁棒激波捕捉能力的空间离散格式.

加权本质无振荡(weighted essentially nonoscillatory,WENO)格式[3]是一种经典的高阶精度激波捕捉格式,以WENO-JS 格式[4]为代表,广泛应用于包含激波和复杂光滑结构可压缩流动问题的数值模拟[5-9].虽然WENO-JS 格式能够捕捉强激波,但对于气动声学问题耗散过大.针对WENO-JS 格式耗散过大、极值点附近精度降阶和计算定常激波不收敛等问题,学者们发展了一系列改进格式,如WENO-M[10],WENO-Z[11],WENO-S[12],WENOSYMBO[13],WENO-SYMCU[14],WENO-ZS[15]和TENO[16]等.

紧致格式也是一种典型的高精度高分辨率数值方法.Lele[17]系统研究了两类线性中心紧致格式: 网格结点型紧致格式(cell-noded compact schemes,CNCS)和网格中心型紧致格式(cell-centered compact schemes,CCCS).CNCS 格式具有零耗散和低色散特性,广泛应用于不含激波的湍流和气动声学问题数值模拟.然而,在实际的计算中,零耗散会导致计算不稳定,需引入人工耗散或者滤波.

为了能够捕捉激波,基于Lele[17]提出的网格中心型紧致格式,结合WENO 格式的激波捕捉思想,Deng 等[18]设计了五阶精度的加权紧致非线性格式(weighted compact nonlinear scheme,WCNS).WCNS 格式具有与WENO-JS 格式相当的激波捕捉能力和较小的耗散,以及更灵活的通量选择.Zhang等[19]将WCNS 格式拓展到了更高阶精度,并且在构造网格中心处的数值通量时,是直接对通量进行插值,而不是对守恒变量或原始变量进行插值后再构造通量.

CNCS 格式和CCCS 格式在构造过程中,都只用了设计模板上的部分信息,格式精度和分辨率不能达到最优.Liu 等[20]设计了一类新型线性中心紧致格式(cemtral compact schemes with spectral-like resolution,CCSSR),该格式在求解网格结点上的函数导数时,将网格结点上的函数值和网格中心处的函数值全部引入,精度最高可达14 阶,并且接近谱方法的分辨率.随后,刘旭亮等[21]以六阶精度的线性中心紧致格式(CCSSR-L-6) 为基础,通过迎风/对称混合型加权非线性插值(WENO 插值)计算网格中心处的数值通量,构造了能够捕捉强激波的迎风/对称混合型加权非线性紧致格式,记为CCSSRHW-6 格式.

为了能够捕捉强激波,增强格式在计算时的稳定性,CCSSR-HW-6 格式在其构造网格中心处数值通量的过程中包含两级加权: 一是五点迎风模板插值和六点对称模板插值的加权;二是内部子模板插值的加权.两级加权的权系数都不是固定值,而是非线性的函数.两级加权虽然增强了格式的耗散自适应能力和激波捕捉能力,但也会使格式形式变得复杂,非线性效应增强.数值格式的非线性效应会导致流场中产生非物理的寄生波[22-24],严重影响气动噪声问题的高保真计算.在大多数激波噪声问题中,激波的强度并不是很高,CCSSR-HW-6 格式的超强激波捕捉能力并不总是必需的,这就为一定程度上放宽激波捕捉能力的要求,进而降低格式的非线性效应和提高格式的分辨能力留出了空间.

本文通过优化CCSSR-HW-6 格式中第一级加权的自由权系数,使其取能够让格式空间分辨能力达到最优的固定值,从而简化格式的构造,减小格式的耗散误差和非线性效应,使其更适合于激波噪声问题的数值模拟.

1 加权优化紧致格式设计

1.1 迎风/对称混合型加权非线性紧致格式

现有的CCSSR-HW-6 格式是在具有类谱分辨率的六阶精度线性中心紧致格式(CCSSR-L-6)的基础上,结合迎风/对称混合型WENO 插值技术发展而来.图1 是格式构造模板.具体构造过程[21]如下.

图1 迎风/对称混合型加权非线性紧致格式的构造模板Fig.1 Candidate stencils of hybrid upwind/symmetric weighted nonlinear compact scheme

六阶精度的线性中心紧致格式(CCSSR-L-6)的表达式为

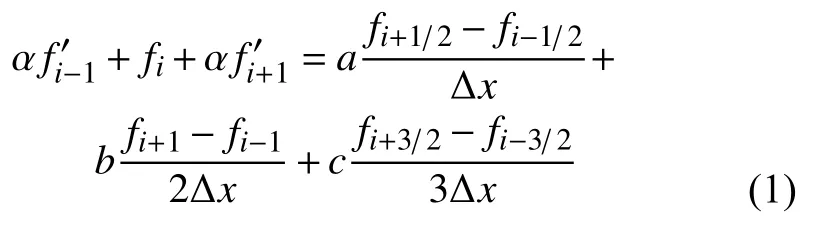
在内部点上,采用隐式格式,系数取值为

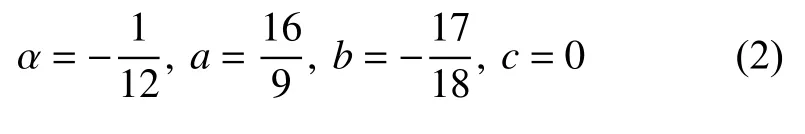
在边界点上,采用显式格式,系数取值为

在CCSSR-L-6 格式中,网格中心上的函数值或数值通量是未知的.为了能够捕捉激波,基于网格结点上的函数值,采用迎风/对称混合型WENO 插值得到网格中心上的函数值.迎风/对称混合型WENO插值技术包含两级加权: 一是五点迎风模板插值和六点对称模板插值的加权;二是内部四个子模板插值的加权.

(1) 第一级加权是五点迎风模板插值和六点对称模板插值的加权,具体如下

(2) 第二级加权是四个内部子模板上插值的加权,具体如下

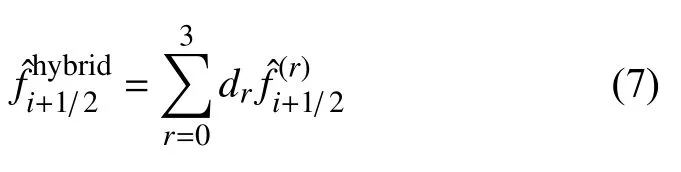
其中,dr是子模板上的第二级权系数.

子模板上的3 阶精度线性插值多项式为

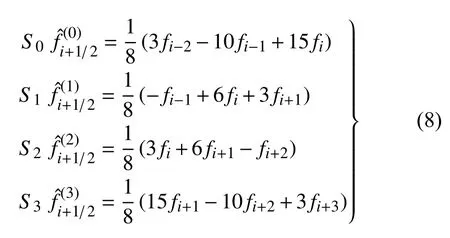
联立式(4)和式(7)可建立两级加权的权系数之间的关系

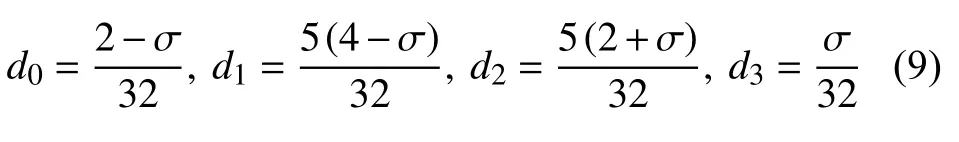
以上内容即为CCSSR-HW-6 格式的线性部分.

(3) 非线性权的构造,具体如下:

第一级权系数 σ 定义如下[21]

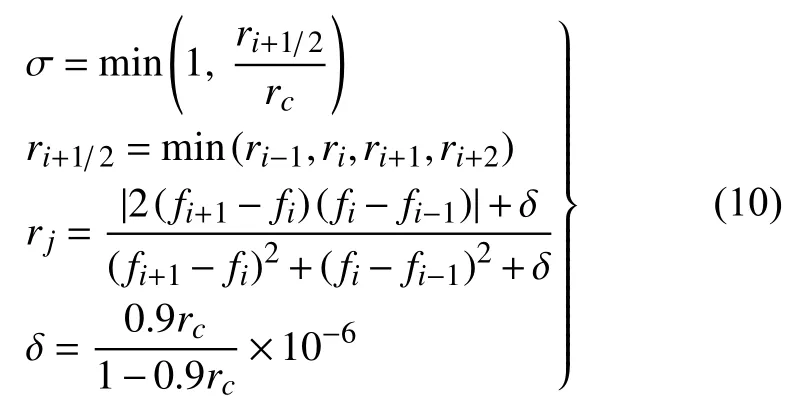
式中,rc是常数阈值,其值越大,数值格式的耗散越大.CCSSR-HW-6 格式将其取值为rc=0.5.

相应的非线性权[21]为

式中,ε是小值正数,作用是避免分母为零,具体取值为ε=1.0×10-40.引入参数C的目的是增大最优线性权的贡献,其值的增大或减小仅会改变数值格式的耗散误差.参数C的值越大,数值格式的耗散误差越小.在处理含有激波的问题时,过大的C值可能会导致离散格式的数值不稳定,CCSSR-HW-6 格式将参数C取值为C=5.

内部四个子模板上的光滑指示因子[21]为

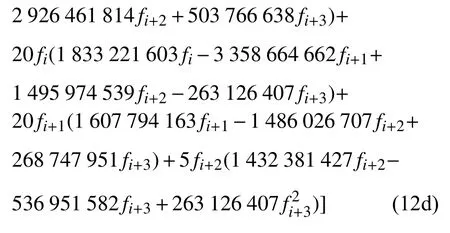
参考光滑指示因子[21]定义为

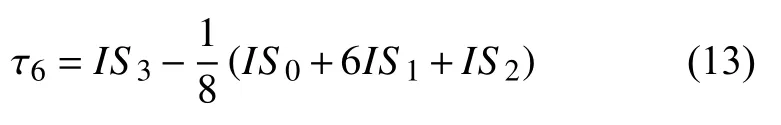
此外,非线性权会导致格式在特定的极值点处损失精度.为解决CCSSR-HW-6 格式在极值点处可能存在的精度降阶问题,CCSSR-HW-6 格式还引入了映射函数[10]

使得非线性权 ωr在临界点处尽量接近线性权dr,从而还原格式的近似精度.

CCSSR-HW-6 格式的两级加权确实增强了格式的耗散自适应能力和激波捕捉能力,但也使格式的形式变得复杂,非线性效应增强.对于大多数激波噪声问题,激波的强度并不是很高.因此,可以通过固定CCSSR-HW-6 格式中第一级加权的权系数取值,简化格式构造,降低格式的耗散误差,减弱格式的非线性效应,提高格式的分辨能力.

1.2 分辨能力优化

本文以CCSSR-HW-6 格式线性部分的修正波数为基础,采用修正波数的误差积分函数[13,25-26]为空间分辨能力优化目标函数,通过优化,固定第一级加权权系数的取值,使格式的空间分辨能力达到最优.格式优化过程具体如下.

第一步,推导CCSSR-HW-6 内点格式和边界格式线性部分的无量纲修正波数.

CCSSR-HW-6 格式线性部分无量纲修正波数的计算方法如下:

考虑纯粹的谐波函数

这里,x是位置,k是波数.

谐波函数的解析导数为

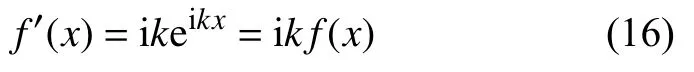
定义n为任意整数,Δx是网格间距,则有

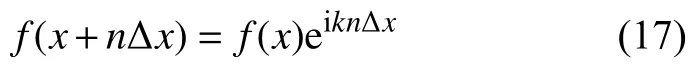
一般有限差分方法的近似导数可表示为

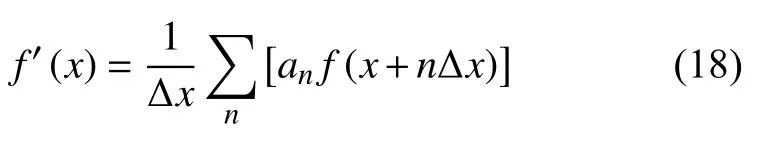
其中,系数an是由差分格式中的系数决定.

定义无量纲波数为 κ=kΔx,结合式(16)～式(18)可得无量纲修正波数的一般表达式

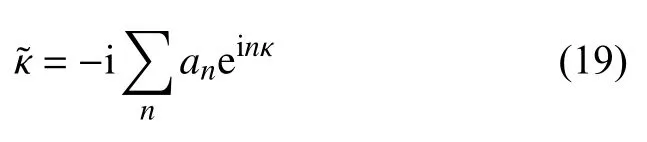
利用上述方法可以得到CCSSR-HW-6 格式线性部分的无量纲修正波数.

对于CCSSR-HW-6 内点格式,无量纲修正波数表达式为

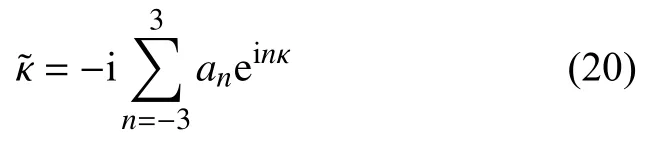
式(20)中的系数如下

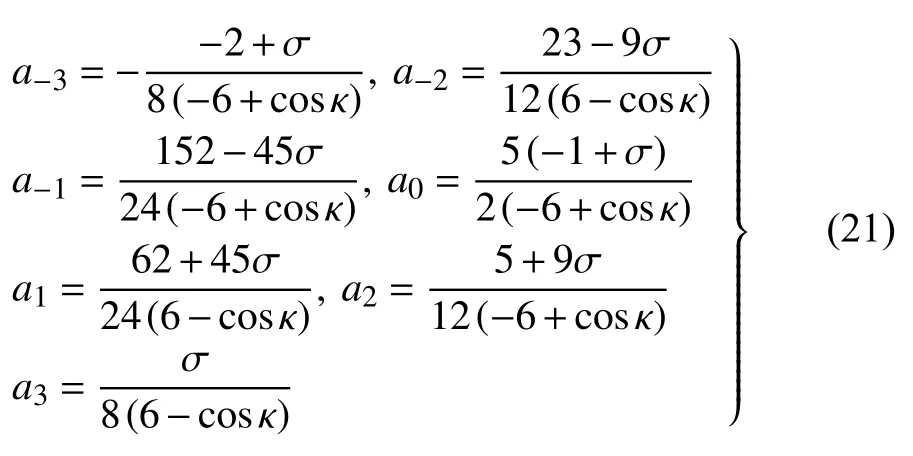
对于CCSSR-HW-6 边界格式,无量纲修正波数表达式为

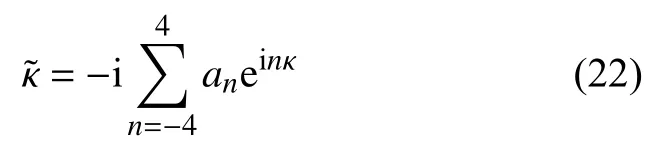
式中的系数如下

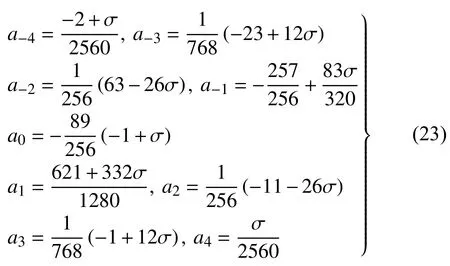
第二步,确定空间分辨率优化目标函数.

数值格式修正波数的实部表征了色散误差(相位误差),虚部则表征了耗散误差(幅值误差).为了对CCSSR-HW-6 格式进行优化,确定空间分辨率优化目标函数为修正波数的误差积分函数.修正波数的误差积分函数综合考虑了数值格式的色散误差和耗散误差.

无量纲修正波数的误差积分函数[13,25-26]表达式为

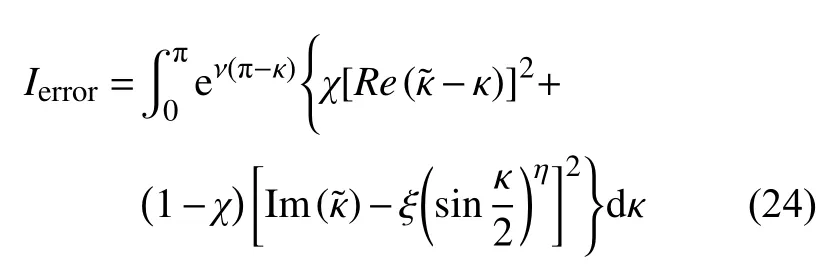
其中,χ,ν ,ξ 和 η 是优化控制参数.

第三步,设置恰当的优化控制参数.

优化控制参数在误差积分函数中分别具有不同的作用[13]: 参数χ控制相位误差和幅值误差的权值;参数 ξ 控制了为确保格式稳定而增加耗散的正弦项;参数 ν 影响数值格式在低波数区的误差;参数 η 影响数值格式在高波数区的误差.

在本文中,优化控制参数的取值与文献[13]相同,分别为第四步,执行优化程序,得到优化结果.

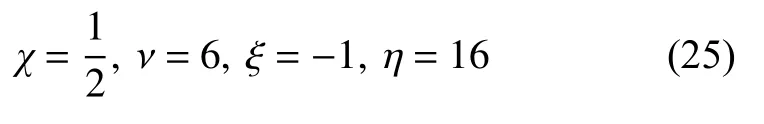
选择优化算法,执行优化程序,确定第一级加权的权系数取值,使得修正波数的误差积分函数取最小值.

第一级加权的权系数优化结果:

内点格式优化系数

边界格式优化系数

经过空间分辨能力优化后的迎风/对称混合型加权非线性紧致格式称之为加权优化紧致格式(weighted optimization compact scheme,WOCS).

2 精度验证

通过一维标量方程算例对加权优化紧致格式(WOCS 格式)的收敛精度进行数值验证.时间推进采用三步三阶TVD Runge-Kutta 方法[4].

一维线性标量方程

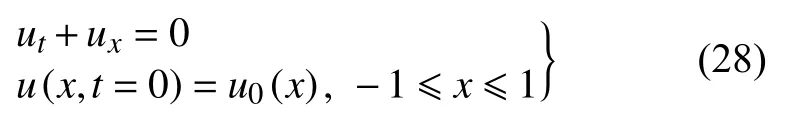
初始条件为

计算采用周期边界条件,总时长为t=1;计算网格由10 逐步加密为160;计算网格为10 时,初始CFL 数为0.5,随着网格的每一次加密,对于r阶格式,CFL 数以因子递减.

表1 列出了WOCS 格式求解该问题时的数值误差和精度阶数.结果显示,WOCS 格式的收敛精度高于5 阶.

表1 加权优化紧致格式的数值误差和精度阶数Table 1 Numerical errors and accuracy order of the weighted optimization compact scheme

3 谱特性分析

数值格式截断误差的精度阶数只能提供数值解向精确解的渐进收敛速率信息,不能给出有限计算网格上的实际误差[27];而差分格式的波传播特性(谱特性)能给出计算网格所支持的Fourier 模态的演化[27].

对于波数为k的单一Fourier 模态,非线性格式不仅会在相同的波数k上产生线性响应,还会在其他波数上产生非线性响应[24,28].对于非线性格式不存在解析的谱关系式,将广泛应用于线性格式的Fourier 分析直接应用到非线性格式的空间分辨能力分析是行不通的.针对非线性格式发展的近似色散关系(approximate dispersion relation,ADR)技术[27]实际上得到的只是非线性格式修正波数的线性响应部分.基于空间导数的修正波数计算方法[24,28]可以得到数值格式的线性响应和非线性响应,具体如下.

非线性格式对于波数k的修正波数为

3.1 线性响应

图2 是WOCS 格式和原CCSSR-HW-6 格式修正波数线性响应部分的对比.线性响应的实部和虚部分别表征色散特性和耗散特性.图2(a)显示,WOCS格式和原CCSSR-HW-6 格式具有相同的色散误差;图2(b)显示,WOCS 格式在中高波数区的耗散误差明显小于原CCSSR-HW-6 格式.总的来说,通过优化使CCSSR-HW-6 格式第一级加权的权系数 σ 取固定值,提高了格式在中高波数区的空间分辨能力.

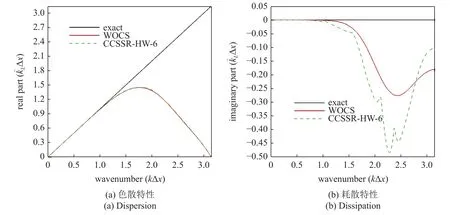
图2 修正波数的线性响应部分Fig.2 The linear response part of the modified wavenumber

3.2 非线性响应

图3 是WOCS 格式和原CCSSR-HW-6 格式的修正波数非线性响应部分的Fourier 系数对比.计算网格点数为N=64,在该网格所支持所有 Fourier 模态中,模态5、模态10 和模态15 是属于中低波数的模态(模态k表示该模态的波数是k).对于任意模态k,非线性格式除了在波数k上会产生线性响应,还会在其他波数 (3+2n)kmodN(N是整数)上产生非线性响应(非物理的寄生波)[24].非线性响应的实数部分代表寄生波的波数响应,虚数部分代表寄生波的幅值响应.图3 显示,在中低波数区间,WOCS格式非线性响应的实数部分与原CCSSR-HW-6 格式相当,而非线性响应的虚数部分则明显弱于原CCSSR-HW-6 格式.综合来看,与原CCSSR-HW-6 格式相比,WOCS 格式降低了中低波数区的非线性响应.

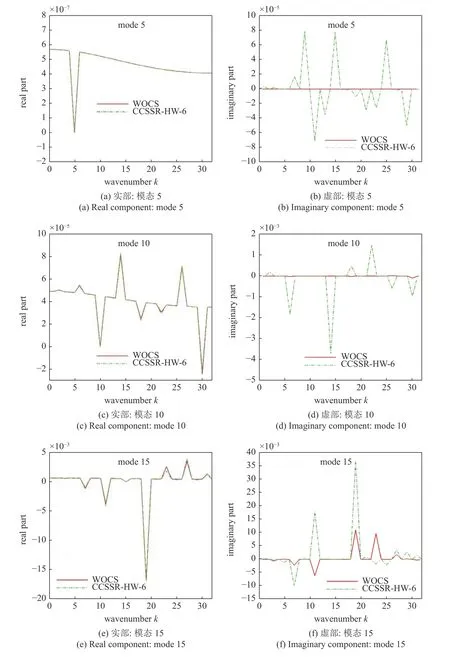
图3 修正波数的非线性响应部分Fig.3 The nonlinear response part of the modified wavenumber

4 数值实验

本节针对加权优化紧致格式(WOCS 格式)在激波噪声问题计算中的适用性进行测试,包括激波捕捉能力、分辨能力和非线性效应.数值实验包括一维Euler 方程算例、二维Euler 方程算例和二维Navier-Stokes 方程算例.无黏数值通量计算采用HLL 型Riemann 求解器[29]或Lax-Fredrichs 通量分裂方法[4],时间推进采用三步三阶TVD Runge-Kutta 方法[4].

4.1 一维Euler 方程算例

(1)激波-声波相互作用

激波-声波相互作用[30]是气动声学中的重要基准问题之一.计算条件如下.

计算域为[0,1],计算网格数为N=401,CFL 数为0.5,计算时长为t=30Tλ;初始时刻,激波位置为xs=0.5,激波马赫数为Ms=2,气体从左向右流动,激波左右两侧的流动变量满足激波关系式.计算域右边界设置为无反射边界条件,在左边界处添加声扰动

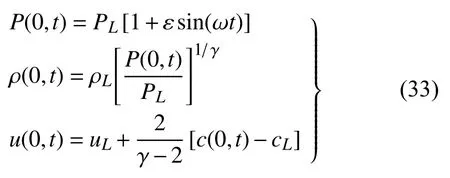
式中参数取值如下

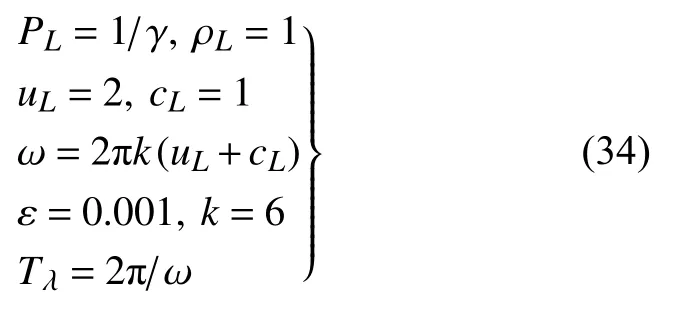
图4 是激波-声波相互作用的数值解及其与参考解的比较.由于解析解是未知的,这里选取五阶精度WCNS-E-5 格式[18]在计算网格数为N=1001 时求解该问题得到的数值解作为参考解.图4(b) 和图4(c) 是图4(a) 的局部放大图.图中的纵坐标δP(t)=P(x,t)-P(x,0)表示声扰动.声波穿过激波后其幅值会被放大.结果显示: 在分辨穿过激波后的声波时,WOCS 格式计算得到的声波幅值与参考解更为吻合,其分辨能力优于原CCSSR-HW-6 格式.

图4 激波-声波相互作用问题的数值结果Fig.4 Numerical results of shock-sound interaction problem

(2)激波-密度波相互作用

激波-密度波相互作用,即Titarev-Toro 问题[31],也是验证数值格式激波捕捉能力和流场细微结构分辨能力的标准算例,在Titarev-Toro 问题中,向右运动的激波(马赫数为1.1)与正弦波形式的高频密度扰动相互作用,产生的流场既包含光滑解,也包含间断.该问题可以看作是激波/湍流相互作用的简化模型.初始条件如下

计算条件: 计算网格数为N=1001,CFL 数为0.5,计算时间为t=5.0;边界条件设置为计算域左、右边界处的守恒变量不随时间变化,这在本算例所感兴趣的计算时长内是适宜的.

图5 是Titarev-Toro 问题的数值解及其与参考解的比较.由于解析解是未知的,这里选取五阶精度WCNS-E-5 格式[18]在计算网格数为N=10 001 时求解该问题得到的数值解作为参考解.图5(b)和图5(c)是图5(a)的局部放大图.结果显示: WOCS 格式数值解的幅值与参考解更为接近,其对高频波的分辨能力远优于原CCSSR-HW-6 格式.这是因为相较于原CCSSR-HW-6 格式,WOCS 格式显著降低了高波数区的耗散误差,如图2(b)所示.

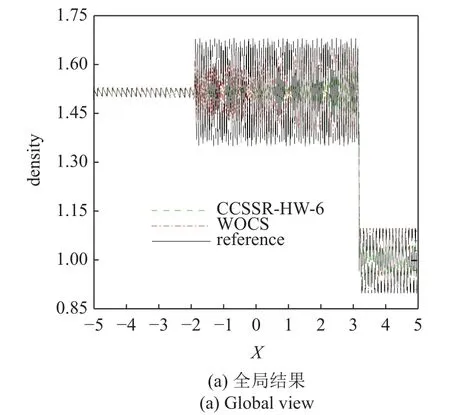
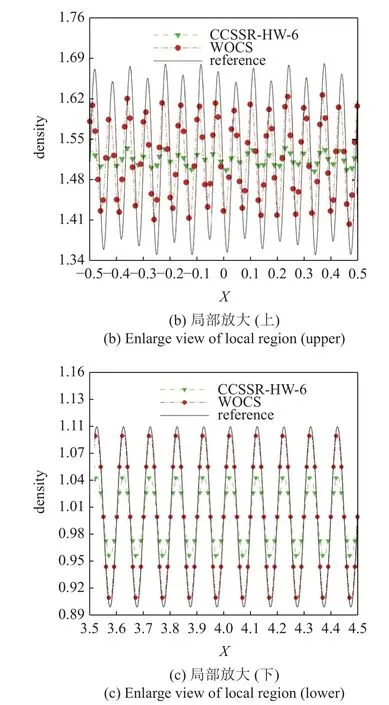
图5 Titarev-Toro 问题的数值结果Fig.5 Numerical results of Titarev-Toro problem

4.2 二维Euler 方程算例

选择激波-涡量波相互作用[32-33]作为二维Euler方程测试算例,该问题是激波-湍流相互作用的二维简化模型.在此算例中,马赫数为Ms=8 的运动激波与散度为零的倾斜涡量场发生相互作用.计算域范围: (x,y)∈[-1.5,1.5]×[-1,1],均匀计算网格,网格间距为 Δx=Δy=0.01 ;计算时长t=0.2.

初始时刻,激波位于x=-1 处,传播速度为

这里的cs1是波前声速(下标1 表示波前状态,下标2 表示波后状态).

波前(x≥-1)初始状态为

波后(x≤-1)初始状态为

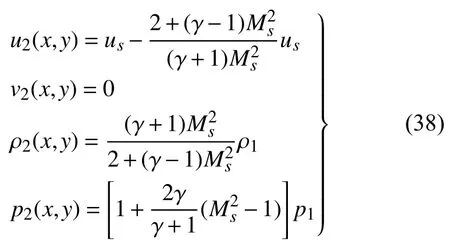
边界条件设置: 在y方向,上、下两端采用周期边界条件;在x方向,左端为超声速入流条件,右端为无反射边界条件.

图6 是采用WOCS 格式计算激波-涡量波相互作用得到的t=0.2 时刻的涡量空间分布.图7 是t=0.2时刻直线y=0 上的涡量分布及其与参考解的比较.参考解是在计算网格数为N=961 × 641 条件下采用CCSSR-HW-6 格式计算该问题时得到的数值解.结果显示: WOCS 格式的数值解与参考解要更为接近,分辨能力优于原CCSSR-HW-6 格式.

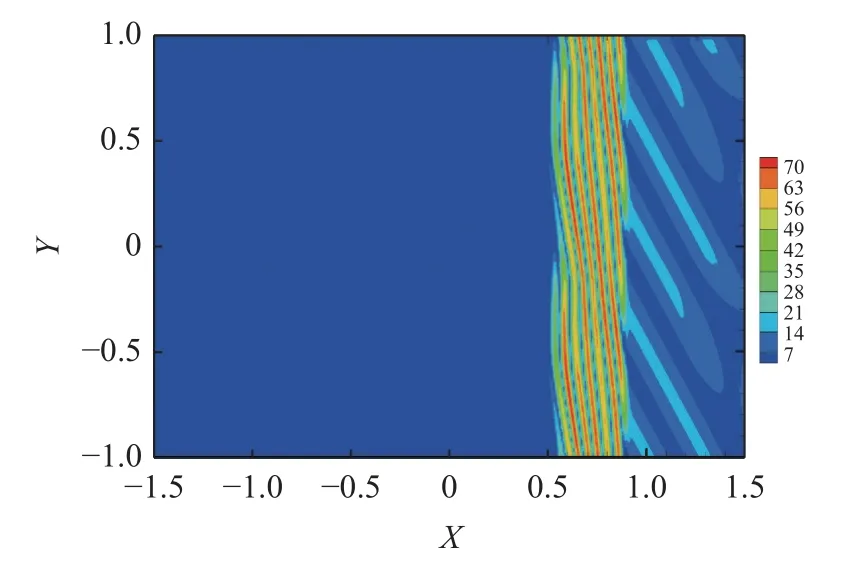
图6 激波-涡量波相互作用在t =0.2 时刻的涡量空间分布Fig.6 The spatial distribution of vorticity in the shock-vorticity wave interaction at t =0.2

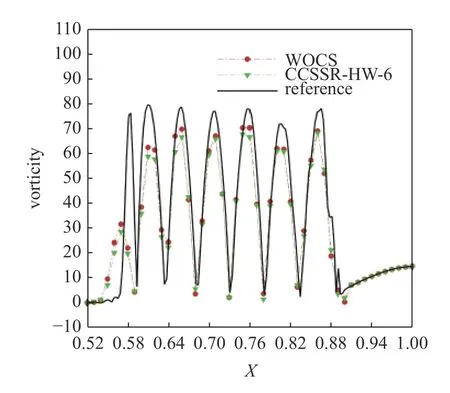
图7 激波-涡量波相互作用在t =0.2 时刻沿直线y=0 的涡量分布Fig.7 The vorticity distribution along the line y=0 in the shockvorticity wave interaction at t =0.2

4.3 二维Navier-Stokes 方程算例

二维Navier-Stokes 方程测试算例选取的是激波-强旋涡相互作用问题[6,34].激波-旋涡相互作用是重要的激波噪声理论研究模型,文献[6,34]对此问题进行了深入细致的研究.此外,该问题也被广泛用作高精度数值方法的验证算例[35].下面简要介绍该问题计算细节.

计算域范围: (x,y)∈[-20,8]×[-12,12],均匀计算网格,网格点数为N=701 × 601,计算总时长t=10.普朗特数Pr=0.75,参考温度T∞=300 K .雷诺数Re=800,具体定义为Re=ρ∞a∞R/μ∞,其中,R是涡核半径,ρ∞,a∞和 μ∞分别是激波前流动的平均密度、声速和黏性系数.初始条件设置如下.

激波马赫数为Ms=1.2,固定在xs=0 的位置.激波前(x≥0)的状态参数为

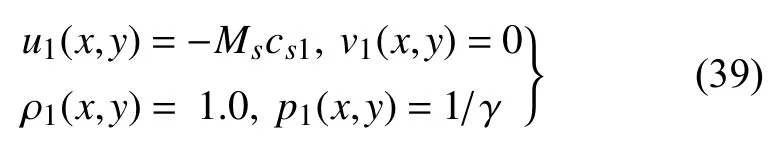
激波后(x＜0)的状态参数为

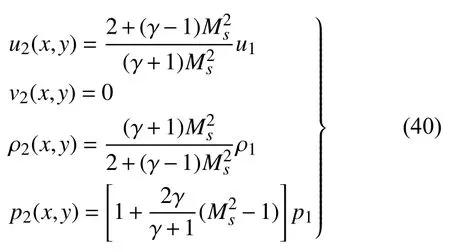
初始时刻,旋涡位于激波波前,其从右向左穿越激波的过程中与之发生相互作用,产生并向外辐射声波.初始涡心位置是 (xv,yv)=(2,0),旋涡强度为Mv=1.0.旋涡的速度、密度和压力分布如下

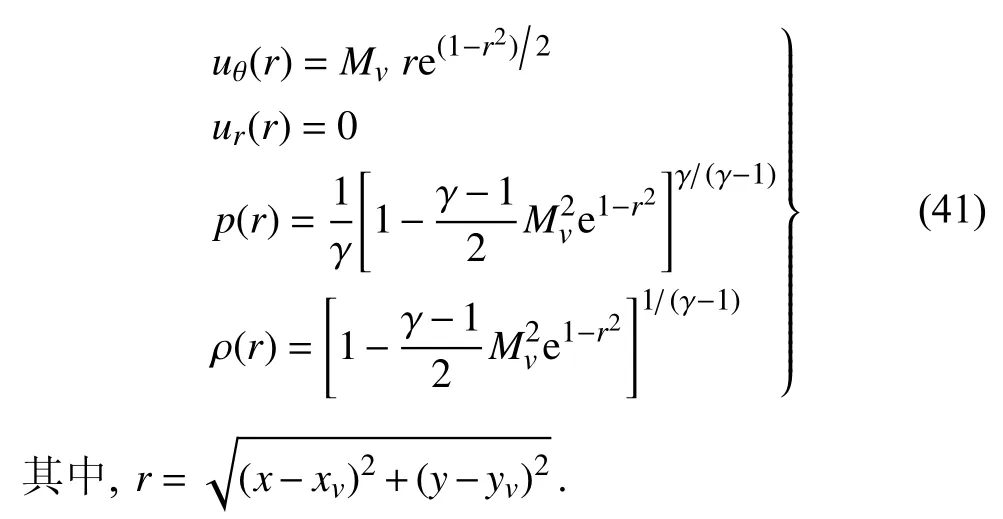
边界条件设置: 在y方向,上、下两端采用周期边界条件;在x方向,右端为超声速入流条件,左端为无反射边界条件.

对于气动声学问题,胀量(速度的散度,∇·V)和数值阴影(∇2ρ)常用来表征声场和流动结构.图8是采用WOCS 格式计算激波-强旋涡相互作用得到的t=10 时刻的胀量空间分布,从中可以看到向外辐射的声波.图9 是t=10 时刻胀量和数值阴影沿径向(θ=π/4,θ 的定义见图8)的分布及其与参考解的比较.参考解是在计算网格数为N=1401 × 1201条件下采用CCSSR-HW-6 格式计算该问题时得到的数值解.对于胀量,WOCS 和CCSSR-HW-6 两种格式的计算结果一致;而对于数值阴影,WOCS 格式的计算结果优于原CCSSR-HW-6 格式的计算结果,其与参考解要更为接近.

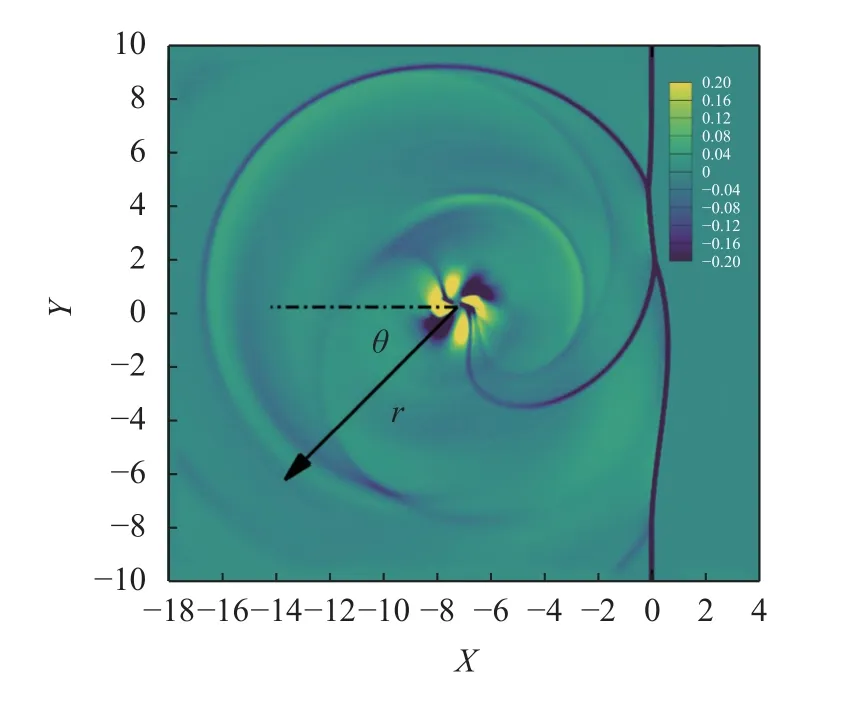
图8 激波-强旋涡相互作用在t=10 时刻的胀量场Fig.8 The dilatation field of shock-strong vortex interaction at t=10

图9 激波-强旋涡相互作用在t =10 时刻的胀量和数值阴影沿径向的分布Fig.9 The radial distribution of dilatation and numerical shadowgraph in shock-strong vortex interaction at t=10

图10 是分别采用WOCS 格式和CCSSR-HW-6 格式计算激波-强旋涡相互作用得到的t=10 时刻的数值阴影空间分布.结果显示: 在CCSSR-HW-6格式计算得到的数值阴影中存在非常明显的非物理振荡,而WOCS 格式计算得到的数值阴影则更为“干净”,上述非物理振荡被显著地减弱.文献[22-24]指出激波捕捉格式在计算时的非线性执行会导致非线性效应,使得数值解中产生此类非物理波动.前文3.2 节中的格式非线性响应分析已经表明,与原CCSSR-HW-6 格式相比,经优化后,WOCS 格式的非线性响应显著降低,由此可以解释这两种格式计算结果之间的差异.

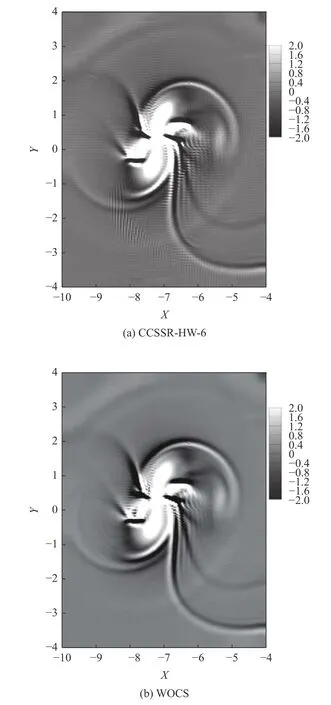
图10 激波-强旋涡相互作用在t=10 时刻的数值阴影Fig.10 Numerical shadowgraph of shock-strong vortex interaction at t=10

5 结论

基于对称模板的迎风/对称混合型加权非线性紧致格式在其构造过程中包含两级加权,并且两级加权的权系数都是非线性函数,格式非线性效应较强.为了减弱格式的非线性效应,改进格式的谱特性,本文基于六阶精度的迎风/对称混合型加权非线性紧致(CCSSR-HW-6)格式,以修正波数的误差积分函数为优化目标函数,通过优化第一级加权的权系数,使其取分辨能力最优的固定值,建立了加权优化紧致格式,记为WOCS 格式.针对WOCS 格式的精度、谱特性和激波噪声问题计算的适用性进行了数值验证.

精度验证表明WOCS 格式的精度高于5 阶.谱特性分析包括了线性响应和非线性响应.线性响应分析表明WOCS 格式在中高波数区的耗散特性明显优于CCSSR-HW-6 格式.非线性响应分析表明:与CCSSR-HW-6 格式相比,WOCS 格式降低了中低波数区的非线性响应.

激波噪声计算适用性的测试算例包括了激波-声波相互作用、激波-密度波相互作用、激波-涡量波相互作用以及激波-强旋涡相互作用.数值实验结果表明: 与原CCSSR-HW-6 格式相比,WOCS 格式不仅降低了耗散误差,提高了对高频波的分辨能力,而且显著地减弱了格式的非线性效应和由此导致的数值解的非物理振荡,较为适合于激波噪声问题的数值模拟.