基于改进粒子群优化的旋翼无人机PID参数整定算法

卢艳军，郭竟翔，李忠海

(1.沈阳航空航天大学自动化学院，辽宁 沈阳 110136；2.辽宁通用航空研究院，辽宁 沈阳 110136)

0 引言

随着科技水平的发展，小型旋翼无人机凭借可操作性强、机动性高、可稳定悬停等优点广泛应用于地形勘察、影视拍摄等领域来代替人类进行各种工作[1-2]。 多旋翼飞行器采用串级比例积分微分(proportion integration differentiation，PID)控制方法，因此PID参数整定就成为了保证动态性能和稳定性的关键要素[3-4]。在实际工程应用之中，由于旋翼无人机具有非线性、强耦合和欠驱动等特性[5]，传统人工整定无人机PID控制参数的方法太过繁琐，只能通过经验法来进行试凑，效率低下且参数较差[6-7]，因此无人机的参数整定是一个亟待解决的问题。

PID参数整定法早在1942年就被提出，随着智能算法的广泛应用，利用其进行PID参数整定优化的方法受到了国内外学者的关注。文献[8]使用基于频域分析算法(FFT)和神经网络方法来自适应整定闭环系统的参数，证实了大部分实际工程中基于闭环系统的输入-输出响应的PID整定方案是可取的；文献[9]利用现有的智能算法，提出和验证了在9种不同的非线性控制系统下，PID 参数整定方法的普遍适用性；文献[10]提出一种改进模糊粒子群控制方法，并且通过6种复杂测试函数的验证，验证了该方法的有效性；文献[11]利用改进粒子群算法应用于数学模型传递函数方程问题，证明该算法的正确性，继而验证该方法可以对于无人机参数进行辨识，并且有很好的鲁棒性。但上述研究仅关注了寻优速度和参数精度对比，却忽略了收敛精度的问题。

本文基于上述研究方法和思想，在其基础之上提出一种改进粒子群优化方法，使用复杂的测试函数验证改进粒子群算法的有效性，利用其对无人机控制系统的PID参数进行整定。

1 四旋翼原理及模型

1.1 四旋翼的工作原理

本文采用四轴“×”形无人机为研究对象。为抵消自身的反扭矩，防止飞机出现自旋现象，无人机相邻机翼旋转方向相反，保证了自身的稳定性。无人机可以通过对不同电机的转速进行调节控制来完成滚转、俯仰和偏航等一系列姿态转换。

无人机机体、惯性坐标系转换如图1所示。为了更好地描述四旋翼无人机的运动，需要将各种运动量以及所受到的力转换到统一坐标系下进行分析，建立对应坐标系并且明确各个坐标系之间的相互转换关系。

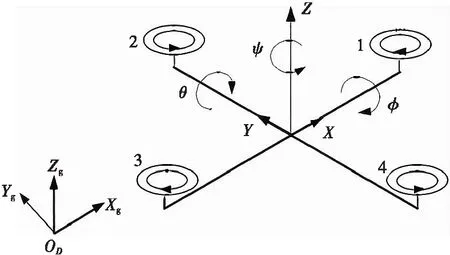
图1 机体坐标系和惯性坐标系Fig.1 Aircraft coordinate system and inertial coordinate system

为了解决上述问题，本文引入欧拉角概念。四旋翼无人机在运动过程中会产生三种角度，其中滚转运动产生滚转角φ，俯仰运动产生俯仰角θ，偏航运动产生偏航角ψ。p、q、r分别代表滚转角、偏航角和俯仰角的角速度。角速度变换如式(1)所示，三次欧拉角变换矩阵如式(2)所示。

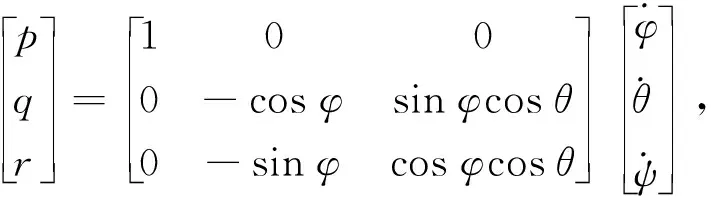
(1)

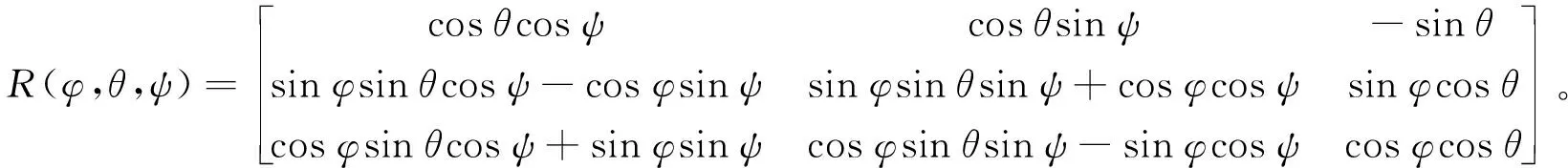
(2)

因为无人机系统处于一种强耦合的状态，以姿态控制环节为例说明，四旋翼无人机姿态采集传感器包括加速度计、陀螺仪、磁力计。当外界突然有风、磁场等干扰时，加速度计和陀螺仪采集到的数据将会出现失真，这种情况下不能准确解算出欧拉姿态角，故而不能使用单级PID回路控制。由于角速度值变化灵敏，完全能够跟随无人机姿态的变化。鉴于此种情况，四旋翼无人机采用双环串级PID控制系统[12-13]。

多旋翼无人机采用分层多环控制，外层控制器为内层控制器提供指令，即将外环控制器所得到的输出值作为理想值。姿态控制是位置控制的基础，只要姿态控制能够被很好地实现，位置控制的问题自然会迎刃而解。

1.2 模型的建立

四旋翼的飞行动力由4个不同的电机提供，可视作系统的4个输入，但其在空间上具有3种平面运动和3种空间转动，即总共有6个方向的输出，因此可视作是一个4输入6输出的欠驱动系统。

常规的四旋翼无人机的动力学模型[14]如式(3)所示。Jx、Jy、Jz是x，y，z方向的转动惯量，φ为滚转角，θ为俯仰角，ψ为偏航角，m为无人机质量，g为重力常数，Ct则是升力系数，Cm是反扭矩力系数，l为半轴距。

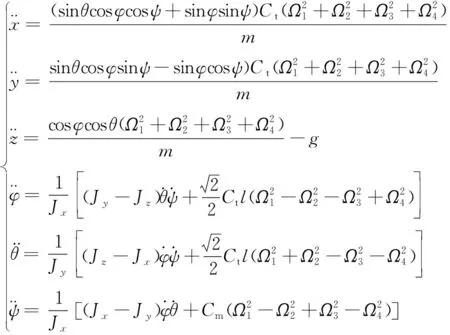
(3)

无人机的状态比较复杂，具有非线性和较强的耦合性，直接对其进行分析可能会比较难，为了简化模型便于求解无人机的传递函数，将其近似模拟在稳定悬停的状态下进行飞行，忽略实际情况中的较小的非线性因素，重力常数g视为不随着高度而变化，同时也不考虑气动效应以及陀螺效应，采取最小扰动法对无人机的数学模型和传递函数进行求解。

将无人机的各个部分都视为刚体。常见的刚体姿态描述方法是欧拉描述以及矩阵描述，文中采用矩阵描述的方法。同时根据升力与转速的平方成正比的数学关系，在小角度偏转和较低的飞行速度下，无人机简化控制模型公式[14-15]为

(4)

式(4)中，τφ、τθ、τψ为3个方向上的力矩，V为电压，b为电机拉力系数，d为电机扭力系数，J为电机转动惯量，Ω为电机转速，Tm为时间常数。该无人机的相关飞行参数如表1所示。

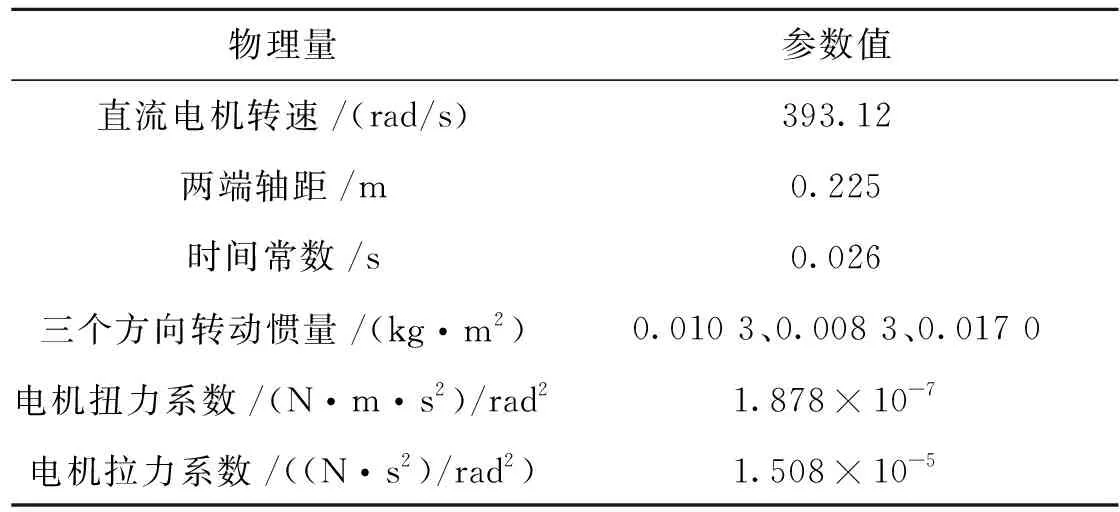
表1 飞行器参数Tab.1 Aircraft parameters

根据文献[14—15]中已有的简化成为对角矩阵的计算方法，利用Matlab代入上述各个相关参数求解得到无人机传递函数的状态空间表达式：

(5)

2 粒子群优化算法(PSO)

2.1 常规PSO方法

2.1.1基本概念

粒子群算法是一种启发式算法，在1995年被美国学者Kennedy和Eberhart共同提出[16]，其思想是利用信息共享原则，以群体感知个体，从单一到具体，从混沌到有序，使其在整个空间域中得到可行解。

粒子群算法的更新迭代公式如下：

(6)

式(6)中，ω是惯性权重(因子系数)，ω取值区间为[0.9，1.2]，通常取值为0.9；c1是个体学习(加速)因子；c2是社会学习(加速)因子；r1、r2是区间[0，1]内的随机值；t一般为1。在整个求解空间中，每个粒子通过不断更新个体极值xpbest和全局极限值xgbest来确定粒子的速度和方向，朝着目标函数值运动。

2.1.2算法实现流程图

粒子群算法的流程图如图2所示。

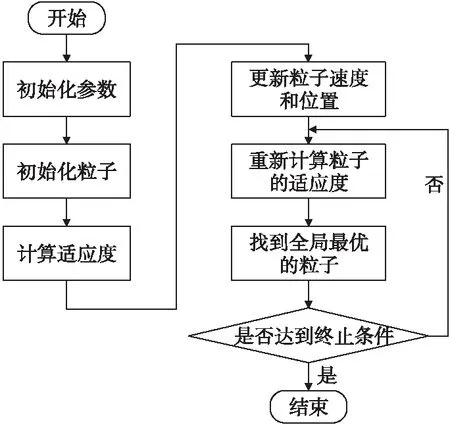
图2 粒子群算法流程图Fig.2 Flow chart of particle swarm optimization algorithm

2.2 改进PSO方法

在经典PSO算法中，优化后期粒子的多样性显得较为缺乏，同时也会提前收敛到局部极值[17-18]，因此可以通过调整学习因子和惯性权重的大小，在搜索的初期，在整个求解空间中进行大范围的搜索，继而获得多样性更好的高质量粒子，在搜索后期小范围调整提升精度，并减小或消去局部极值的影响。

在考虑和解决实际优化问题时，人们对于惯性权重的取值方式通常是线性递减，但PSO的搜索过程极其复杂，并非单一的线性递减，因此本文采用一种具有动态惯性权重的非线性递减PSO算法，改进后的速度更新公式如下：

(7)

式(7)中，ωmin和ωmax是预先给定的最小及最大惯性系数，一般取值为0.4和0.9；i是迭代次数(iteration)，imax是最大迭代次数。

在Kennedy和Eberhart提出的粒子群算法中，c1和c2的取值在2左右较为合适。考虑到学习因子对算法的影响因素，本文采用一种降低自身经验参数，提高群体经验参数，并且c1和c2随时间改变而发生变化的方法。关于c1和c2的改进如下所示：

(8)

式(8)中，c1i、c2i、c1f、c2f分别为c1、c2的迭代初值和终值。如表2所示，将寻优得到的最优解与已知真正的最优解进行误差比较，经过多次实验，结果表明，当c1从2.5降低到0.5，c2从0.5上升到2.5时，最有利于搜索最优解，既保证了搜索能力，提高了数据的收敛精度，又能明显降低搜索优化时间。

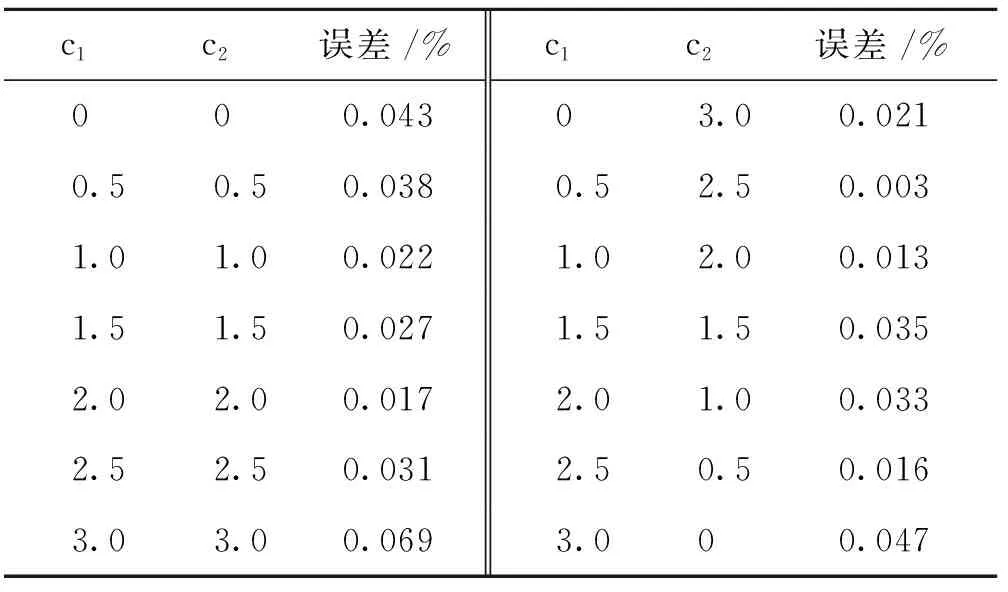
表2 实验误差Tab.2 Experimental error

2.3 改进PSO方法的性能分析

很多优化算法需要利用测试函数来检验算法的可靠性和鲁棒性，常用的测试函数一般包括多维度、多峰值的特点。在学术界，通常用某些固定的测试函数来验证提出的优化函数的质量。所有测试函数都是连续的，可以根据它们的特性分为四类[19]，如表3所示。

表3 测试函数的分类及特点Tab.3 Classification and characteristics of test functions

表3第三类和第四类主要用于检验智能优化方法，例如GA、PSO、TS、SA等。为了验证本文提出的改进粒子群算法的优化性能，选择两个不同的基准函数Acklex函数和Rastrigin函数[19]，对算法的优化性能进行综合测试，这两个函数是被使用频率最高的两个函数，并将算法改进前后的优化结果进行比较。

Acklex函数表达式为

式中，-8≤x≤8。

该函数为一个n维函数，具有较多的局部最小值，函数在(0,0)处取得最小值0。该函数具有较难辨别搜索方向的特点，查找全局最优解较为困难，Ackley的函数图形如图3所示。

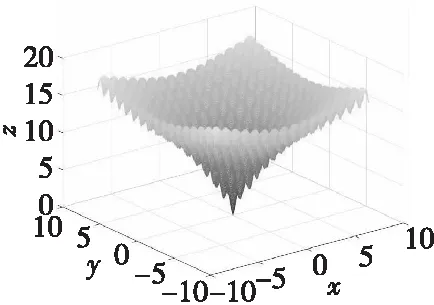
图3 Acklex函数图像Fig.3 Image of Acklex

Rastrigin函数表达式为

式中，-2≤x≤2。

该函数具有较多的局部极值，波形峰谷交替，难以求解到最优值，最值的位置坐标为(0,0)，测试函数如图4所示。

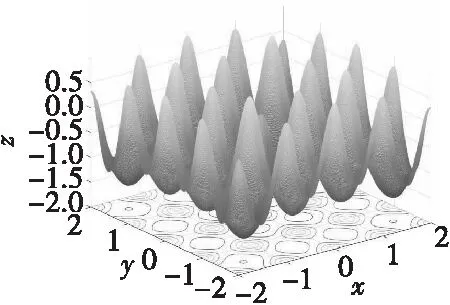
图4 Rastrigin函数图像Fig.4 Image of Rastrigin

首先进行初始化处理，粒子群种群规模设置为20，终止迭代步数设置为200，其中原始粒子群算法的w初值设置为0.9，c1、c2初值设置为2；改进粒子群算法的w初值设置如式(7)所示，c1、c2初值设置如式(8)所示。

如图5所示，分别是使用改进前后的粒子群算法针对于Acklex函数和Rastrigin函数的寻优曲线走势图。

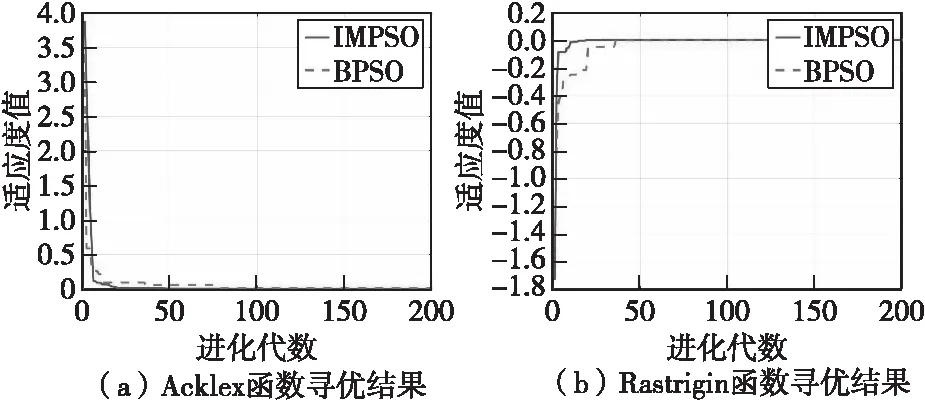
图5 寻优曲线走势图Fig.4 Trend chart of optimization curve

根据图5可以看出，改进前后优化的收敛效果都比较好，对于测试函数起到了较好的寻优效果，但是相对于BPSO(discrete binary particle swarm optimization algorithm)算法，IMPSO(improved particle swarm optimization algorithm)算法的收敛速度相对较快，找到最优解所需要的迭代步数更短。通过Matlab的计算结果得知，改进算法的收敛精度也相对之前的方法大大提升，距离最值点(0,0)的误差在10-5级别。

综上所述，IMPSO算法对于两个不同测试函数的优化结果都要优于BPSO算法，从而验证了改进算法的可行性和解决优化问题的普遍适应性，为该方法融入到无人机参数整定优化的过程提供了可行的依据。

3 改进粒子群算法PID整定仿真结果分析

3.1 仿真模型建立

由于无人机姿态的改变都是通过各个电机转速的不同而实现的。众所周知，无人机的内环是角加速度环，外环则是角速度环，为了方便研究，忽略内外环节之间的负载效应，使得内外环节相互关联[20-21]。使用Simulink对文中无人机的系统模型进行等效模拟。

搭建的实验仿真模型如图6所示。三个通道分别代表单级、串级控制参数整定前和串级控制参数整定后。三个姿态角的仿真框图均如图所示，但是仿真结构中的传递函数和内外环参数各不相同。

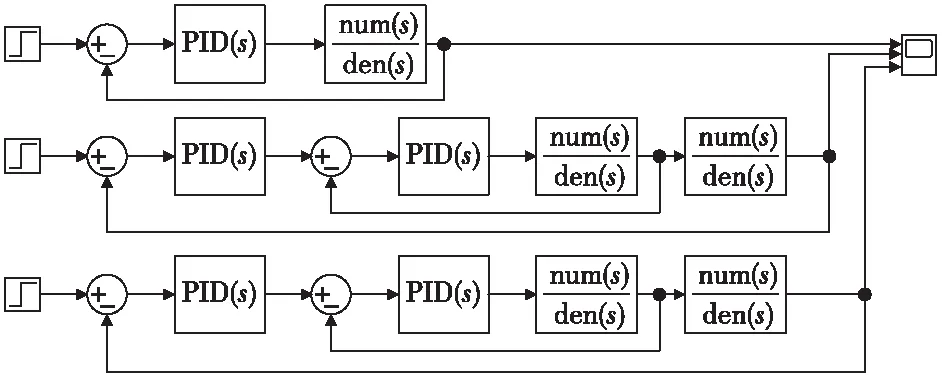
图6 动态响应仿真模型Fig.6 Simulation model of dynamic response

3.2 控制参数的确定

传统的人工整定方法难以快速获得良好的控制器参数，因为其都是通过经验法试凑得到的，整定时间较长且参数效果不佳[22]，因此本文用改进粒子群来对PID参数进行优化整定。首先确定适应度函数确定参数的大致范围，内环和外环参数PID参数的范围从[0，0，0，0，0，0]到[10，10，10，10，10，10]。利用粒子群算法对PID控制器参数进行整定优化，通常使用的误差性能指标包括ITAE、ISE、IAE等，本文选用ITAE误差性能指标作为适应度函数，其定义为

(9)

利用改进粒子群方法进行多次迭代，对比控制效果，得到最优的参数集如表4所示。

表4 整定得到的PID参数Tab.4 PID parameters by tuning

3.3 仿真结果

将寻优整定完成得到的PID参数代入图6所示的动态响应仿真模型中，得到结果如图7—图9所示。

图7 俯仰角通道仿真对比图Fig.7 Simulation comparison of pitch angle

图8 滚转角通道仿真对比图Fig.8 Simulation comparison of roll angle

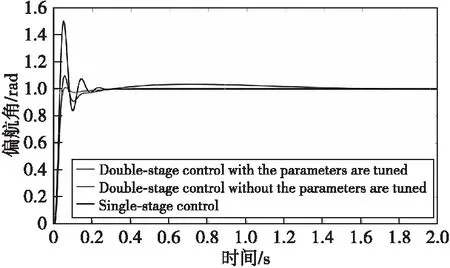
图9 偏航角通道仿真对比图Fig.9 Simulation comparison of yaw angle

由计算得到的直观数据汇总如表5所示。

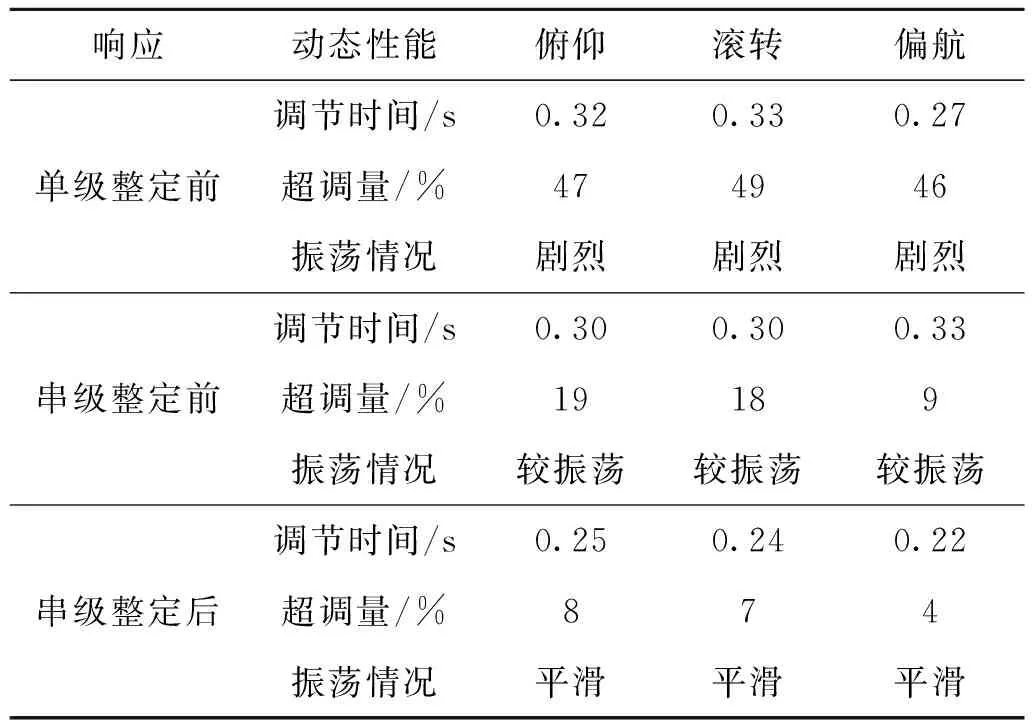
表5 优化前后结果对比Tab.5 Comparison of result before and after optimization

根据上述图表所示结果可以分析得到：

1) 在各个姿态角响应曲线中，单级控制回路的曲线振荡情况比较剧烈，且调节时间稍长一些；而其他两路串级控制响应曲线的调节时间较短，且超调量也要远远小于单级控制。

2) 在两个串级控制回路中，系统使用整定完成的参数后的曲线的动态性能更好，明显优越于参数整定之前，调节时间更短且超调量也更小。

3) 在两个串级回路中，参数整定后相比较于整定前来说，超调量下降大约在60%～70%，调节时间缩短了20%～33%，说明参数整定优化之后，无人机能快速到达稳态，动态性能明显提升。

为了验证整定完成的参数对于控制系统的抗干扰能力，进一步说明本文参数整定优化的正确性和有效性，在仿真通道中分别加入阶跃干扰信号和白噪声干扰信号，分别模拟瞬时强干扰和持续弱干扰情况。图10所示是分别添加两种干扰信号的仿真模型。阶跃干扰信号在T=3 s的时候开始加入，白噪声信号在T=0 s的时候开始加入。

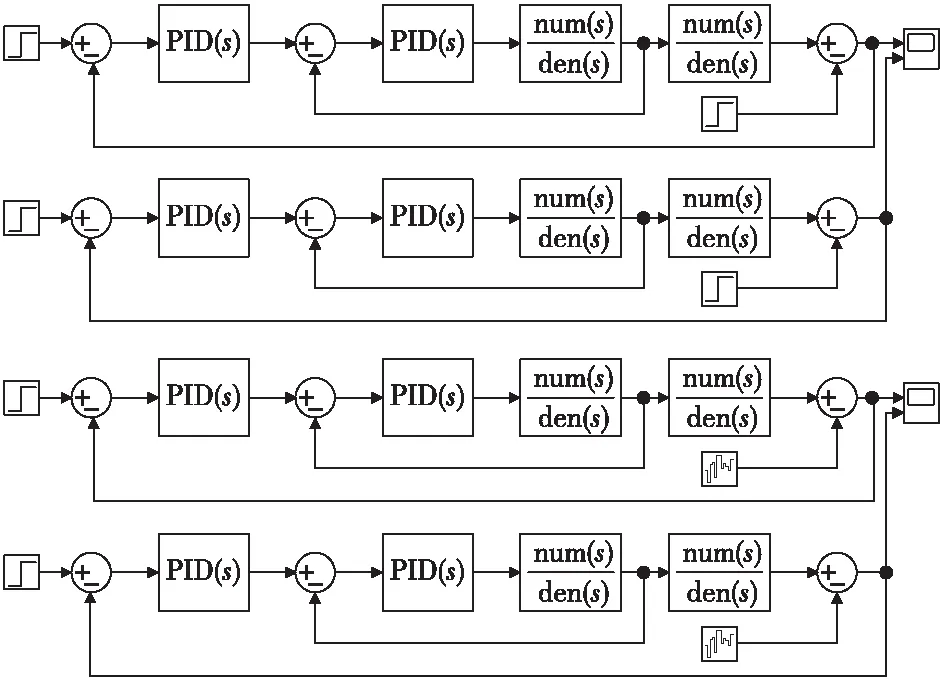
图10 抗干扰仿真模型Fig.10 Simulationmodel of anti-interference

通过图11—图13的仿真效果比较分析可以看出：在两种干扰信号的作用下，使用改进粒子群算法整定得到的参数控制系统抗干扰性能更好，快速性更佳，超调现象较小，曲线恢复至稳态的过程也更加平滑。上述结果均表明了基于该参数组合的系统的抗干扰性能较强，再次验证了基于改进粒子群算法整定得到的参数的优越性。

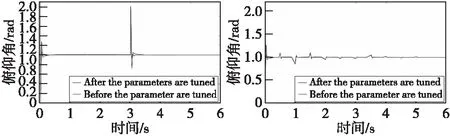
图11 俯仰角抗干扰仿真效果图Fig.11 Anti-interference simulation result of pitch angle

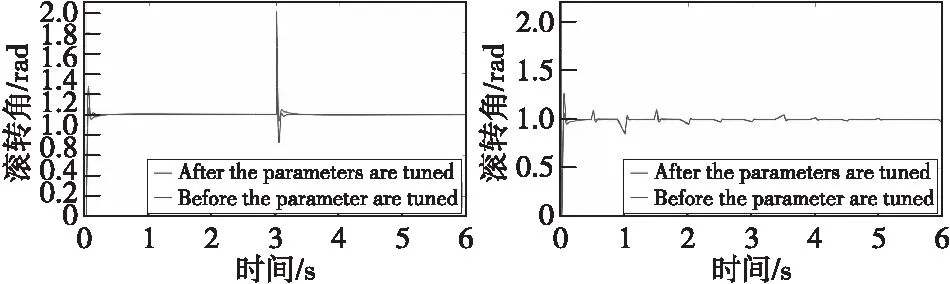
图12 滚转角抗干扰仿真效果图Fig.12 Anti-interference simulation result ofroll angle

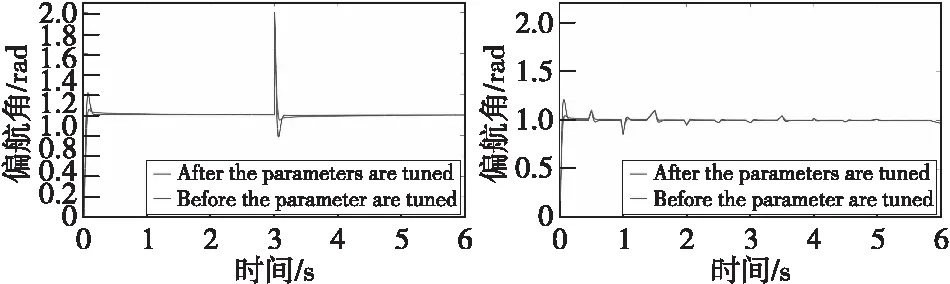
图13 偏航角抗干扰仿真效果图Fig.13 Anti-interference simulation result of yaw angle

为了使本文结论不仅仅停留在理论层面，需要进行实际飞行测试，验证本文的理论结果与实际飞行结果是否相符。首先建立飞行测试系统环节，图14是本次实际飞行测试系统。

图14 飞行测试系统图Fig.14 Flight test system

图15—图17所示是姿态角传感器实际测量的回传数据的可视化分析图，分别显示的是参数整定之前和参数整定之后的无人机飞行姿态角数据。

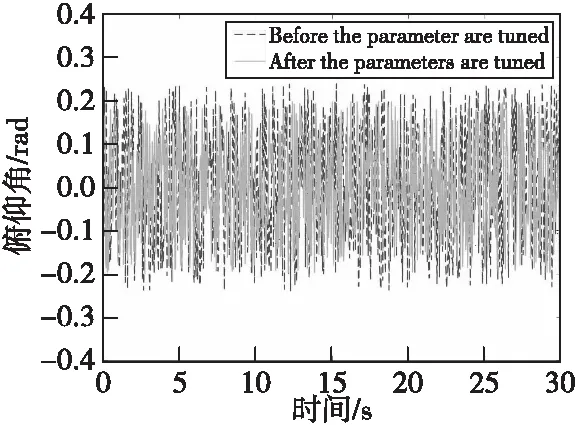
图15 俯仰角传感器数据图Fig.15 Data of pitch angle sensor

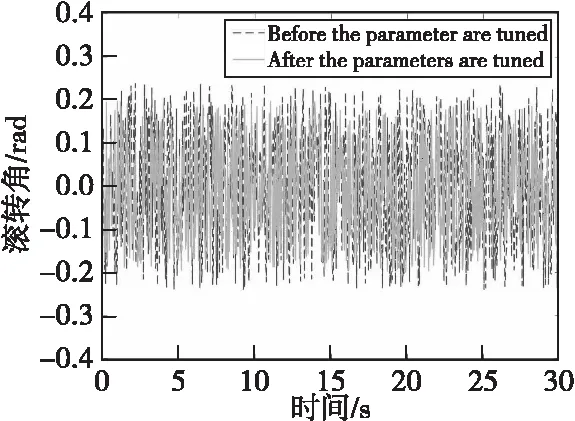
图16 滚转角传感器数据图Fig.16 Data of roll angle sensor

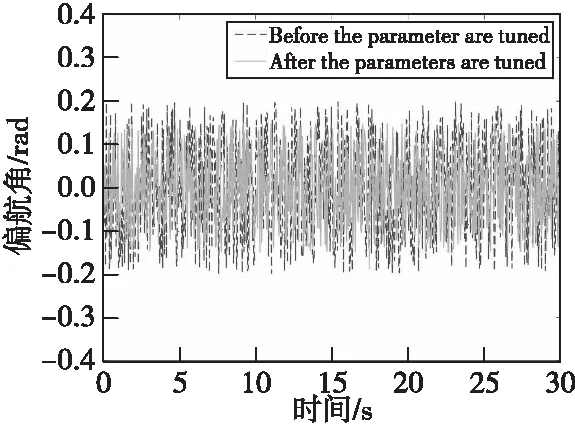
图17 偏航角传感器数据图Fig.17 Data of pitchyaw sensor

对上述三个姿态角数据的分析如表6所示。

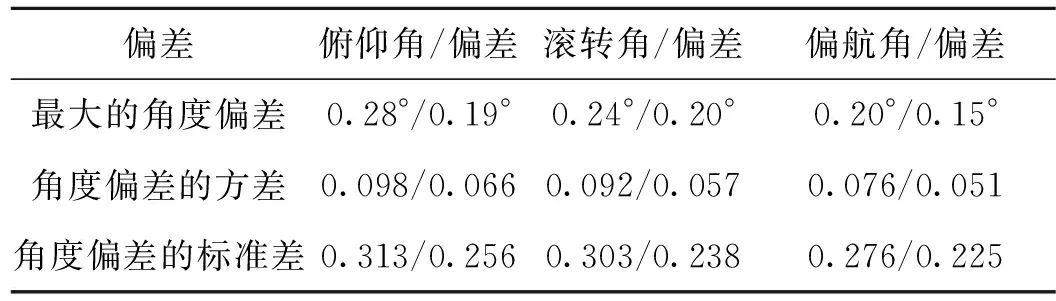
表6 参数整定前后姿态角数据表Tab.6 Attitude angle data before and after parameter setting

根据上述图表的数据分析可以得到：在室外实际飞行环境测试下，使用整定完成参数的无人机系统具有更加良好的稳定性和动态性能，而且在旋翼高速旋转带动飞机震动的情况之下，整定后的系统无人机系统的姿态角变化量更小，与前文的理论结果相符，证实了改进粒子群算法应用在四旋翼无人机参数整定工作的有效性和优越性。

总体来说，通过改进粒子群算法的优化整定后得到的参数所控制的效果相比较于传统方法有了很大的提升，动态性能明显改善，同时也极大地减少了参数整定时间，证实了利用改进粒子群方法对于无人机PID参数进行整定优化的方法是可行的。

4 结论

本文通过改进粒子群寻优算法对无人机PID参数进行整定，减少了参数整定所需时间，避免了人工整定的困难，同时更加方便简捷，提升了无人机的可操作能力和动态性能。

为验证粒子群算法与PID模型的结合效果，使用Matlab/Simulink搭建无人机姿态控制模型并进行仿真。实验结果证明：改进粒子群算法对无人机PID参数整定方法可行，在参数整定优化之后，无人机的动态性能更佳，调节时间缩短了20%～33%；超调量降低了60%～70%，减小了到达稳态过程中的震荡，使得整个过程趋于平滑，抗干扰性能更好，提升了收敛精度。