量子点-金属纳米环杂化系统中量子动力学特性

蔡国庆，刘汉成，程木田

(安徽工业大学电气与信息工程学院，安徽马鞍山 243032)

金属表面等离激元可局域在亚波长尺寸内，进而可突破衍射极限，因而基于金属表面等离激元的纳光子器件引起广泛关注[1-3]。另一方面，量子点具有可集成性等优势，被看成是实现量子计算和量子信息以及量子器件的优良载体[4-5]。因此，金属表面等离激元和量子点之间的相互作用也受到广泛关注，研究者们讨论了采用不同金属纳米结构操控量子点光发射特性[6-7]，发展了局域表面等离激元-量子点复合体系中量子干涉理论[8]，进一步拓宽了微纳尺度的腔量子电动力学[9-10]。

金属环形腔具有超高的珀塞尔因子[11]及较长的表面等离激元传输距离[12]，可支持以驻波模式存在的表面等离激元。基于金属纳米环-量子点耦合系统，学者们对其表面等离激元与激子间的相干相互作用进行了深入研究。Yang等[13]研究了量子点耦合金属纳米环表面等离激元受激辐射而放大；Lin等[14]提出了基于金属纳米环的量子总线且展示了如何实现受控相位门；Chen等[15]针对金属纳米环-量子点耦合系统，讨论当不对称耦合时实现2个量子点的纠缠；Qurban等[16]针对多个量子点与圆环耦合体系，讨论了量子点之间产生最大纠缠的条件，进一步讨论了多个纳米环辅助的手性量子态传输。但前人仅限于讨论等离体子腔被激发的情况，对量子点和表面等离激元的动力学讨论较少。鉴于此，给出不同初始条件下量子点、微腔粒子数解析表达式，分析不同初始条件下2个量子点-金属纳米环耦合系统的量子动力学特性，探讨量子点间纠缠、表面等离激元模式间的纠缠以及量子态转移等，以期为量子点-金属纳米结构复合体系在量子信息处理中的进一步应用提供参考。

1 模型和系统哈密顿量

图1 2个量子点与金属纳米环耦合示意图Fig.1 Schematic diagram of coupling between two quantum dots and metal nanorings

2 纠缠态产生和量子信息转移

2.1 第一种情况，c1(0) = 1

当量子点处于激发态时，通过薛定谔方程可得到4个几率振幅的解析表达式。但由于干涉效应，解析表达式非常复杂。因此，只考虑kd=mπ 和kd=(m+ 1/2)π(m是整数)2 种特殊情况。kd=mπ 时，4 个几率振幅的解析表达式为：

图2 纠缠度C的变化曲线Fig.2 Variation curves of entanglement C

2.2 第二种情况，c3(0) = 1

当环中初始时刻有一个k模式的表面等离激元时(该表面等离激元可通过金属纳米环与表面等离激元波导耦合作用得到)，通过薛定谔方程，同样可得到4个态的复几率振幅表达式，当kd=mπ时，4个态的复几率振幅分别为：

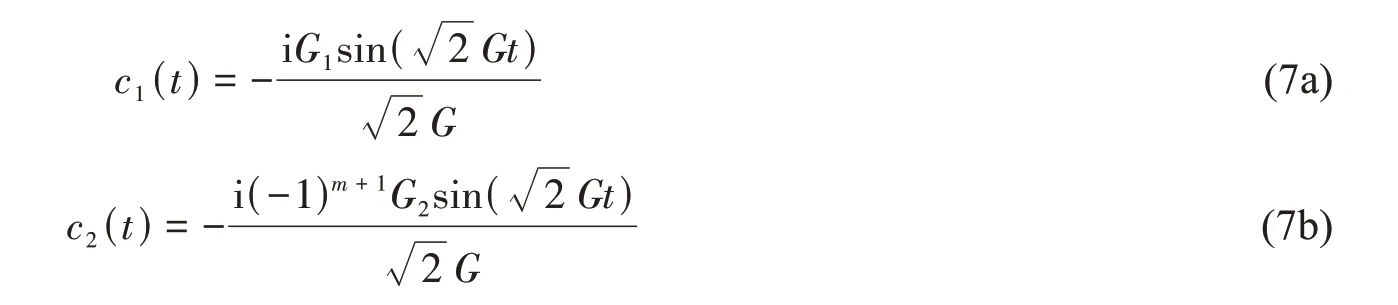
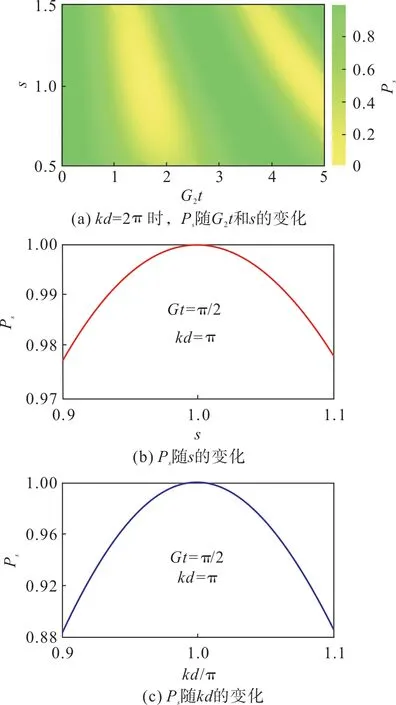
图3 可信度Ps随G2t和s的变化曲线Fig.3 Variation curves of fidelity Ps with G2t and s

图4 2个量子点的纠缠度及粒子数动力学Fig.4 Eentanglement of two QDs and populations dynamics

当kd=(2m+ 1)π/2时，4个态的复几率振幅分别为：

3 耗散对量子点纠缠转移和量子态的影响

上文讨论中，忽略了表面等离激元和量子点的耗散，这些耗散在实际中是不能避免的。为此，在原哈密顿量中加入式(9)来描述耗散的影响[19]。

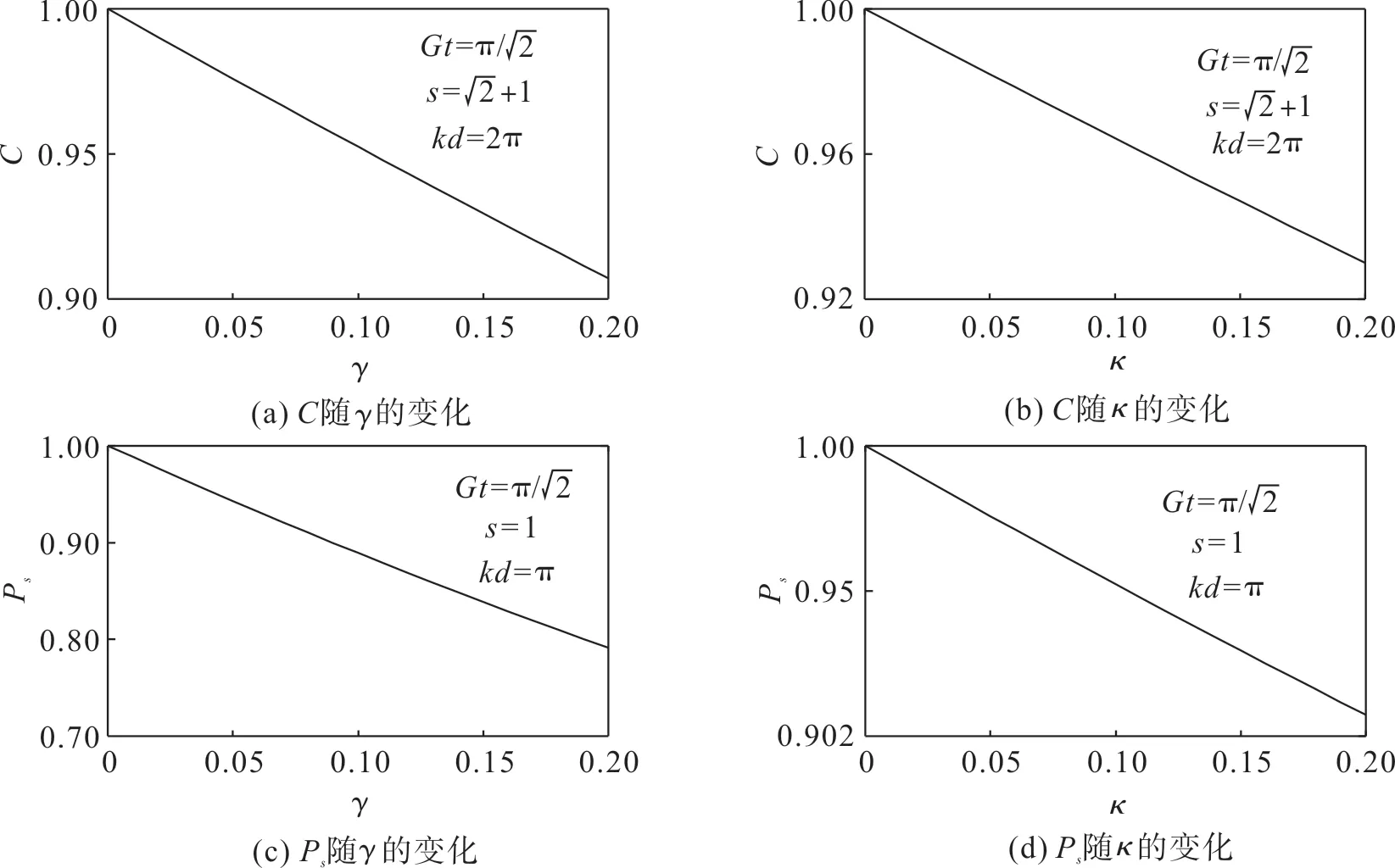
图5 纠缠度C与可信度Ps随γ和κ的变化曲线Fig.5 Variation curves of entanglement C and fidelity Ps with γ and κ

4 结论

研究2 个量子点和金属纳米环耦合系统的量子动力学特性，推导出不同初始条件下量子点和表面等离激元模式的几率振幅解析表达式，得出系统中实现量子点和金属表面等离激元纠缠以及量子态转移的条件。进一步研究表明，即使参量背离理想值，仍可得到较高纠缠度和可信度的量子态转移，这有助于实验中实现量子效应。本文的结果在量子信息及基于表面等离激元的量子器件等方面有一定的应用价值。