面向多目标柔性作业车间调度的强化学习NSGA-II算法

尹爱军，闫文涛，张厚望

(1.重庆大学 a.机械工程学院;b.机械传动国家重点实验室,重庆 400044; 2.中国石油西南油气田分公司 重庆气矿,重庆 400021)

作业车间调度问题(JSP, Job shop scheduling problem)是作业车间系统生产管理的核心部分，在实现制造过程智能化的过程中发挥着重要作用。多目标柔性作业车间调度问题(MO-FJSP, multi-objective flexible job-shop scheduling problem)同时对多个性能指标进行优化，在解决工序排序问题时考虑了工序加工机器选择问题，更加贴近于实际生产环境，因而受到了诸多学者的广泛关注[1-4]。

MO-FJSP是更为复杂的NP-hard问题[5]。Deb等[6]引入快速非支配排序和拥挤距离计算提出了NSGA-II算法，被广泛应用于多目标优化问题求解，但也存在易于早熟和多样性不足等问题，许多学者对该算法做出了改进。Seng等[7]通过计算拥挤度和非支配水平来优化新的种群选择，提出一种基于改进NSGA-II的柔性车间作业低碳调度方法。缪嘉成等[8]针对RV减速器结构优化问题，提出一种离散变量的编码方案改进NSGA-II。陈辅斌等[9]利用免疫平衡原理改进NSGA-II算法的选择策略和精英保留策略，提高了算法的优化性能。胡成玉等[10]提出一种改进拥挤距离和自适应交叉变异的NSGA-II算法求解分布式数据中心负载调度问题，提升了算法收敛速度和精度。以上研究对NSGA-II算法的改进大都采用单一种群的遗传操作模式，进化过程中缺乏激烈竞争关系，难以进化出适应性较强的个体。多种群进化策略可以有效改善算法对解空间的探索能力和开发能力，提高解的多样性和分布均匀性。程子安等[11]提出一种改进的双种群混合遗传算法求解柔性作业车间调度问题，两个种群采用不同的交叉与变异算子以提高种群多样性，然而种群比例参数由人为设定，降低了算法的灵活性。近年来，许多研究将强化学习与智能算法结合应用于实际问题求解，Chen等[12]利用强化学习技术保持遗传算法中种群的多样性，防止GA过早收敛，提出一种基于强化学习的最优RS算法。王晓燕等[13]提出一种基于强化学习的多策略选择遗传算法将种群划分为3个子种群分别进化，提高收敛速度的同时改善了全局收敛问题，但仅优化单个目标。封硕等[14]将支持强化学习RNSGA-II算法应用于无人机多目标三维航迹规划规划问题，通过动态优化种群间迁徙参数保持种群多样性，提高了收敛速度和收敛精度，但遗传操作方式单一减小了局部搜索空间。

根据上述研究内容的优势与不足，提出一种基于强化学习的改进NSGA-II算法用于求解多目标柔性车间调度问题。首先，根据性别判定法和种群比例参数将种群划分为两个不同的种群，并为每个种群分配不同的进化目标与遗传操作，增强算法全局与局部搜索能力。迭代过程中运用强化学习机制动态调整种群比例参数，自主保持种群多样性及分布均匀性在合理范围，有效改善了算法寻优能力与收敛性能。通过对标准算例实验仿真，验证了RLNSGA-II在求解多目标柔性车间调度问题上可以获得较优的Petro解集。

1 多目标柔性作业车间调度模型

MO-FJSP需解决n个工件{J1,J2,…,Jn}的加工机器分配以及在m台机器{M1,M2,…,Mk}(k∈{1,2,…,m})上的加工顺序问题。其中，每个工件Ji(i∈{1,2,…,n})有pi道工序，工序Oij(j∈{1,2,…,pi})的加工时间由所选机器性能决定。调度的目标是在满足加工约束条件下使所期望的多个性能指标得到优化。

调度模型考虑生产效率和设备利用率两个方面，针对最大完工时间(Cm)、机器总负荷(Wt)以及瓶颈机器负荷(Wm)3个指标同时进行优化，调度优化目标集可以表示为min(Cm,Wt,Wm)，其中最小化最大完工时间是为了提高生产效率，而降低机器负荷可以提高机器利用率及机器寿命。目标函数的计算公式如下。

1)最大完工时间。

(1)

2)机器总负荷。

(2)

3)瓶颈机器负荷。

(3)

s.t.

(4)

Cij≤Si(j+1),∀i,j。

(5)

(6)

(7)

Sij≥0,Cij≥0。

(8)

2 RNSGA-Ⅱ算法求解多目标柔性车间调度问题

NSGA-Ⅱ种群进化过程如图1所示。首先对种群Pt执行选择、交叉、变异操作形成种群Qt，并将2个种群合并为种群Rt，然后对种群Rt进行非支配排序形成多个前列面Fi，并从低到高依次加入新一代种群Pt+1，当Fi加入使得种群超出规模大小时，依据拥挤距离从大到小将个体加入新一代种群Pt+1。由于降低了计算复杂度，NSGA-Ⅱ被广泛应用于多目标优化问题。但求解多目标柔性作业车间调度问题时，存在精英选择策略导致种群多样性不足使得算法陷入局部最优解、早熟收敛的问题。因此，笔者通过融合多个多样性度量指标，采用双种群进化策略和强化学习改进NSGA-Ⅱ求解多目标柔性作业车间调度问题。

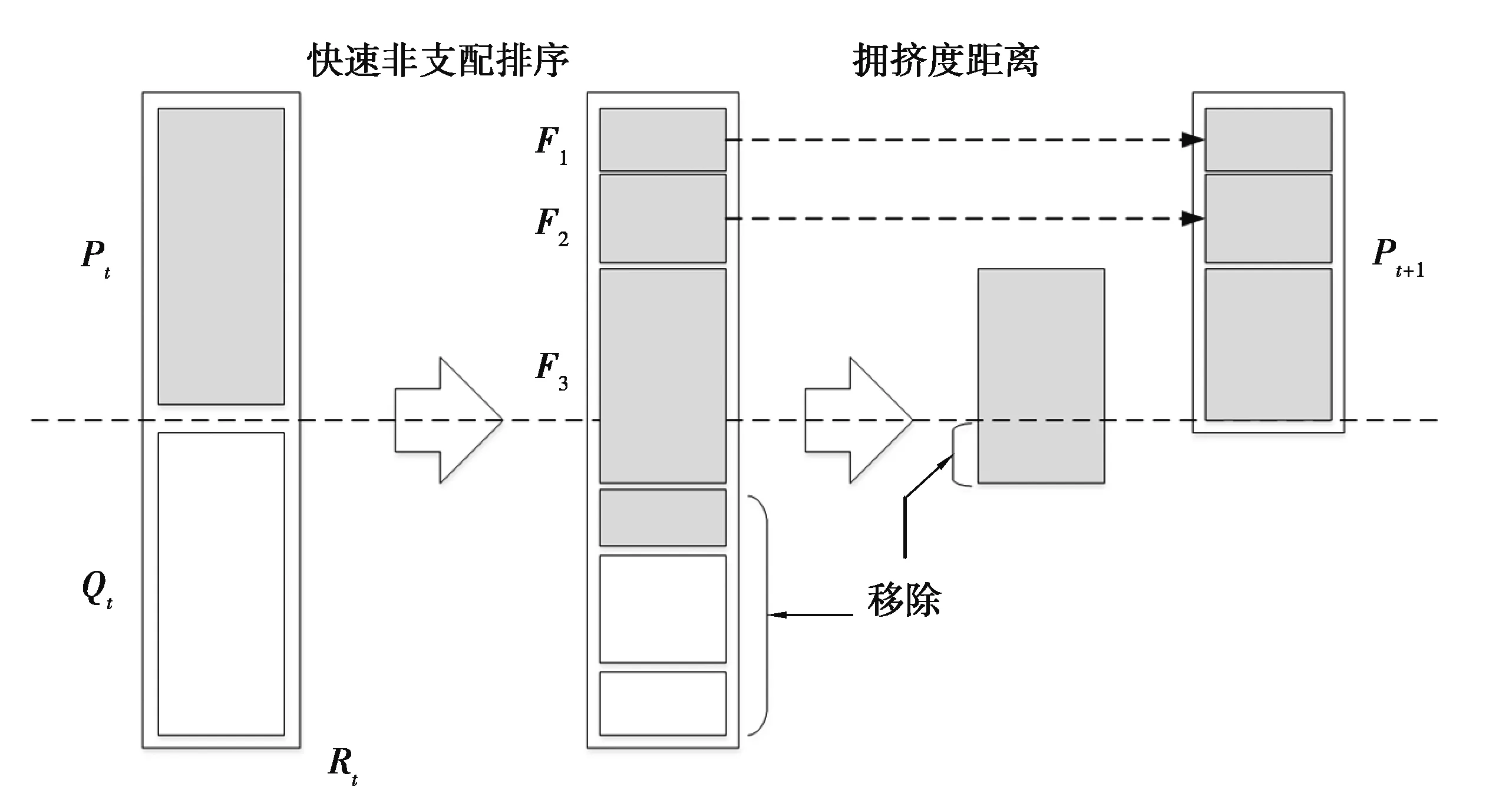
图1 NSGA-Ⅱ种群进化过程Fig. 1 Population evolution process in NSGA-Ⅱ

2.1 双种群进化策略

多目标进化算法大都采用单一进化策略，在一定程度上降低了算法的搜索能力和收敛速度，增加了算法的随机性。采用双种群进化思想可以提高NSGA-Ⅱ进化的方向性和适应性，扩大搜索空间，避免算法陷入局部最优的问题。在进化过程中，根据种群比例参数和性别判定法[15]将种群拆分为两个种群，并对两个种群采用不同的遗传操作。针对多目标优化问题，采用性别判定法拆分种群的流程如下。

1)确定染色体种群规模N、测试种群规模S、种群分割比例参数β。

2)随机生成数量为S的测试种群。

3)计算染色体种群中个体的繁殖能力，具体过程如下。

Fori=1 To N do

Forj=1 To S do

a)个体i与个体j进行交叉操作后产生后代个体；

b)如果后代个体支配个体i，则后代个体替换个体i并将个体i的繁殖能力加1；

End for

End for

4)评判染色体种群中个体的繁殖能力，具体过程如下。

Fori=1 To N do

If(个体i的繁殖能力大于平均繁殖能力)

个体i为繁殖个体；

Else

个体i为普通个体。

End for

5)种群分割。选择繁殖个体中繁殖能力较强的N×β个个体形成子种群1，若数量不够，则挑选普通个体中繁殖能力较强的个体补充；剩余个体形成子种群2。

种群1中的个体由于繁殖能力较强，因此对工序排序部分采用普通的POX交叉和插入变异[16]方式，机器选择部分采用单点交叉和单点变异，从而保持种群的全局优势。而对于种群2，利用普通的遗传操作难以产生新的个体，降低了算法的局部搜索能力，因此对工序排序部分采用改进的POX交叉方式和基因串逆序变异方式，如图2(a)和(b);机器选择部分选择均匀交叉和定向变异方式，以提高算法的收敛能力，如图3(a)和(b)所示。

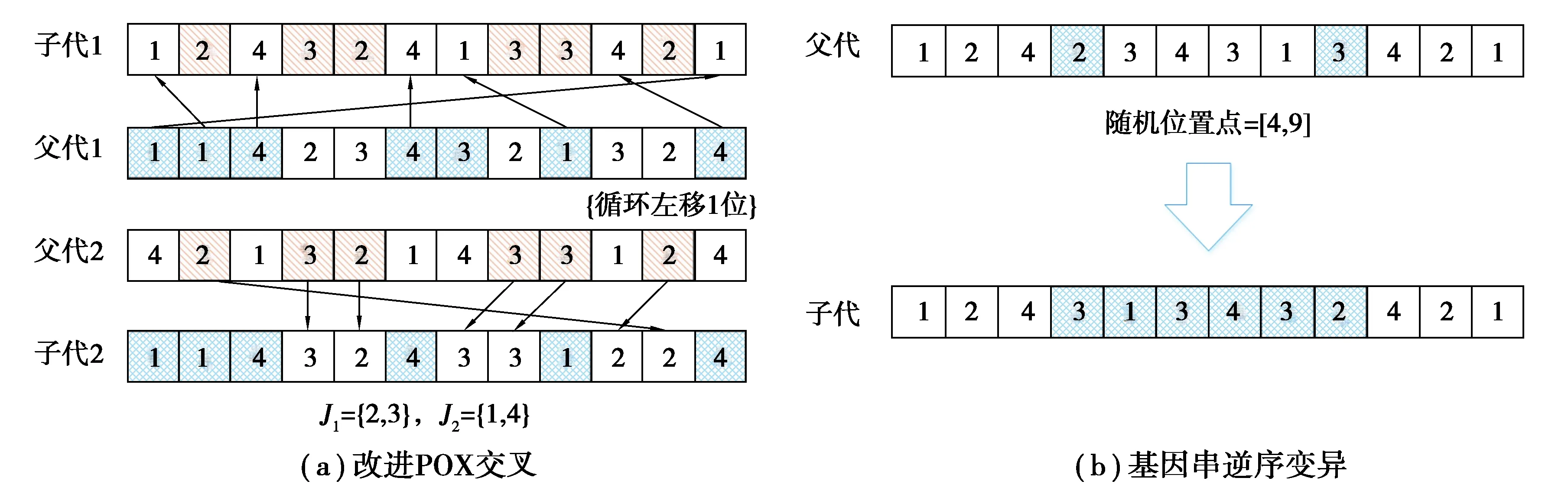
图2 种群2染色体工序部分交叉变异操作Fig. 2 Population 2 chromosome process partial crossover mutation operation

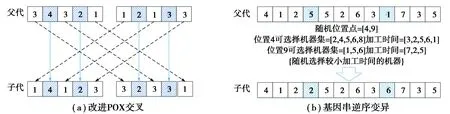
图3 种群2染色体机器部分交叉变异操作Fig. 3 Population 2 chromosome machine partial crossover mutation operation

2.2 多目标问题多样性度量

多目标问题中非劣解集在近似Pareto前沿上分布得越均匀、越离散则表明多样性更好。常用的指标包括[17]Sigma度量、解间距度量、网格度量、熵度量和个体空间度量等。然而，单一评价指标会导致一定程度的偏差。因此考虑解间距和熵度量值两个指标对多样性进行度量，并结合强化学习动态控制种群比例参数，实现多目标柔性车间调度问题优化求解。

2.2.1 解间距度量(spaceing metric)

设算法搜索到的具有Pareto性的前沿解的个数为|A|，则解间距指标Sp定义为：

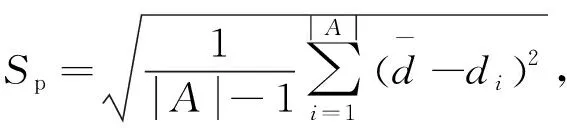
(9)

其中

(10)

2.2.2 熵度量(Entropy)

设种群X有划分X={X1,X2,…,XQ},其中1≤i≤Q,Q为划分数，则

(11)

式中：Pi表示个体i落入第i个划分的概率;|Xi|表示第i个划分的个体数目;N表示整个种群的规模。种群多样性熵的计算公式为

(12)

当熵值越大时，种群中个体分布得越离散、越均匀，种群的多样性也越好。

2.3 基于强化学习的比例参数调整策略

强化学习是一种目标驱动的自适应优化控制方法，智能体Agent通过与环境进行交互来调整自己的行动策略。其最终目标是获得最优策略π*，使得期望累积回报E=[Rs|st=s]最大。强化学习的迭代计算公式为

Q(st,at)=Q(st,at)+α[rt+1+γmaxQ(st+1,at)-Q(st,at)]，

(13)

式中：α称为学习因子；γ为折扣率；r为获得的即时奖励。

将NSGA-Ⅱ中的种群视为Agent，最终目标是比例参数学习，Agent通过感知种群多样性变化来控制种群比例参数，进而控制种群进化方向，当解间距较初始种群减小而熵度量值增加时，种群比例设置合理。强化学习的状态划分、动作设计以及奖赏机制如下。

2.3.1 状态

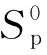
表1 状态集合

2.3.2 动作

强化学习Agent的动作是对种群比例参数的调整，包含增加、不变、减少3种。计算公式如式(14)所示。

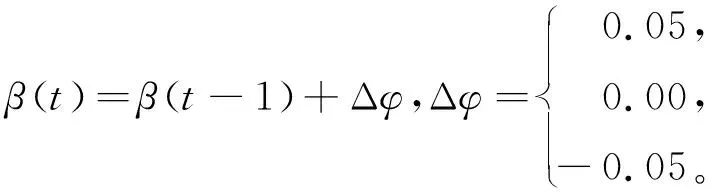
(14)

式中β(t)、β(t-1)分别为第t和t-1代种群的分割比例参数。

依据解间距与熵度量值的变化决定Agent的奖赏，目标是学习最优的比例参数β(t)。具体计算公式为

R=Rd+Re

(15)

(16)

2.4 RNSGA-II算法求解MO-FJSP问题流程

RLNSGA-II算法求解MO-FJSP的流程如图4所示。

图4 基于强化学习的改进NSGA-II算法流程图Fig. 4 Flow chart of improved NSGA-II algorithm based on reinforcement learning

操作步骤如下：

Step1 输入工件信息，设置算法参数：迭代次数G，初始种群比例参数β，种群规模N，交叉概率Pc，变异概率Pm，强化学习Q值表，学习率α以及折扣率γ。

Step2 产生初始种群，计算初始种群解间距值和熵度量值。染色体编码采用基于工序的实数编码方式，分为工序调度与机器选择两部分。

Step3 对种群进行快速非支配排序和拥挤度计算。

Step4 采用性别判定法按照比例参数β拆分种群，通过双种群进化策略获得新一代种群。

Step5 判断是否达到最大迭代次数，如果是，则结束迭代；否则，执行Step6。

Step6 计算种群的解间距和熵值，获得状态st。

Step7 计算奖励值R，根据公式(14)更新Q值表。

Step8 采用ε-贪心策略选择动作at，更新种群比例参数,转到Step3。

3 试验仿真与分析

算法采用C#程序语言在Visual Studio2017软件实现，运行环境为Intel©CoreTMi5-4430 CPU@3.00 GHz。RLNSGA-II算法的参数设置如下：种群规模N=100，最大迭代次数G=200,初始种群比例参数β=0.5,交叉概率Pc=0.8，变异概率Pm=0.1，强化学习的学习率α=0.9,折扣因子γ=0.9。

3.1 算例测试

为验证RLNSGA-II算法求解的有效性，选取Kacem[18]等提出的不同规模的标准算例进行测试，用n×m表示一组n个工件与m台机器的算例，每组算例均独立运行10次，并将运行结果与多策略融合的Pareto人工蜂群算法[19]、改进粒子群算法[20]、混合人工蜂群算法[21]、自适应Jaya算法[22]及基于正态云的状态转移算法[23]的仿真结果进行对比，比较结果如表2所示。

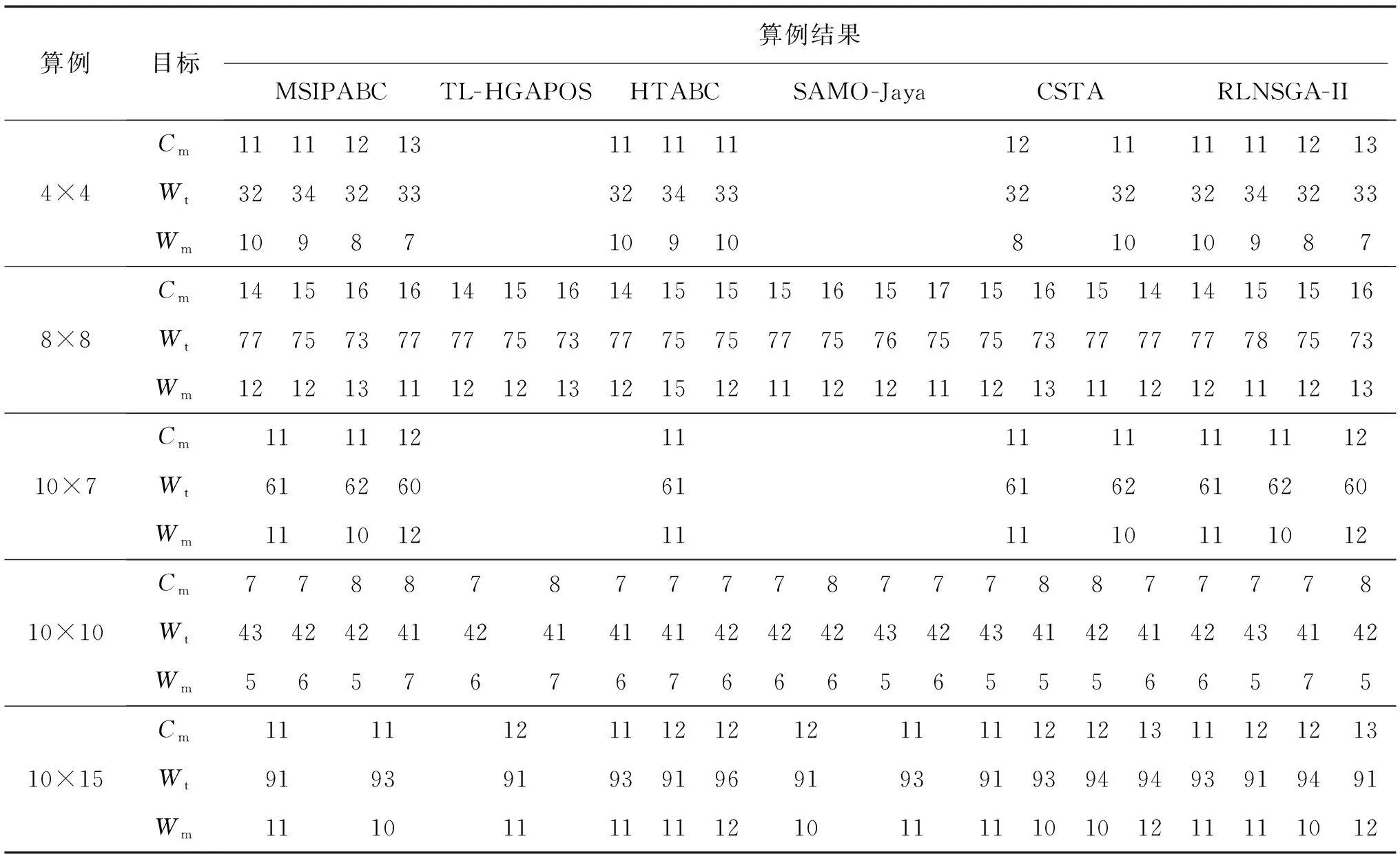
表2 Kacem算例结果对比

通过表2可知，运用RLNSGA-II求解多目标FJSP均可以得到最优组合解，且在总体运行结果和解的多样性上与所提文献中算法的结果基本一致。根据表格中的运算结果， RLNSGA-II算法在求解算例4×4和算例10×7时与MSIPABC算法的结果相同，相比于其他几种优化算法Pareto解更多样且在单个目标值上有所突破；而对于算例8×8和算例10×10，RLNSGA-II的运行结果与MSIPABC、SAMO-Jaya和CSTA相近，但获得Pareto解的个数多于TL-HGAPOS和HTABC算法,且与其相比在Wm优化目标上更优，图5和图6分别展示了RLNSGA-II求解算例8×8和算例10×10运算结果的甘特图；对于算例15×15，RLNSGA-II的运算结果接近于其他几种算法求得的最优解，但解的多样性优于MSIPABC、TL-HGAPOS、HTABC和SAMO-Jaya 4种算法的仿真结果。综合上述分析可知，RLNSGA-II可有效求解柔性作业车间多目标优化调度问题。

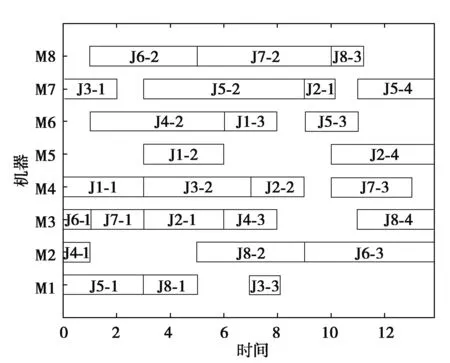
图5 8×8算例甘特图Fig.5 Gantt chart of 8×8 calculation example

图6 10×10算例甘特图Fig.6 Gantt chart of 10×10 calculation example

3.2 算法改进性能分析

为了验证各改进部分对NSGA-II影响， 针对Kacem 8×8算例进行收敛性能及多样性度量指标对比分析。以3个目标函数之和作为适应度值，分别采用NSGA-II、只加入双种群进化策略的改进NSGA-II及RLNSGA-II进行求解，得到收敛性能对比图及多样性度量指标图(如图7所示)。

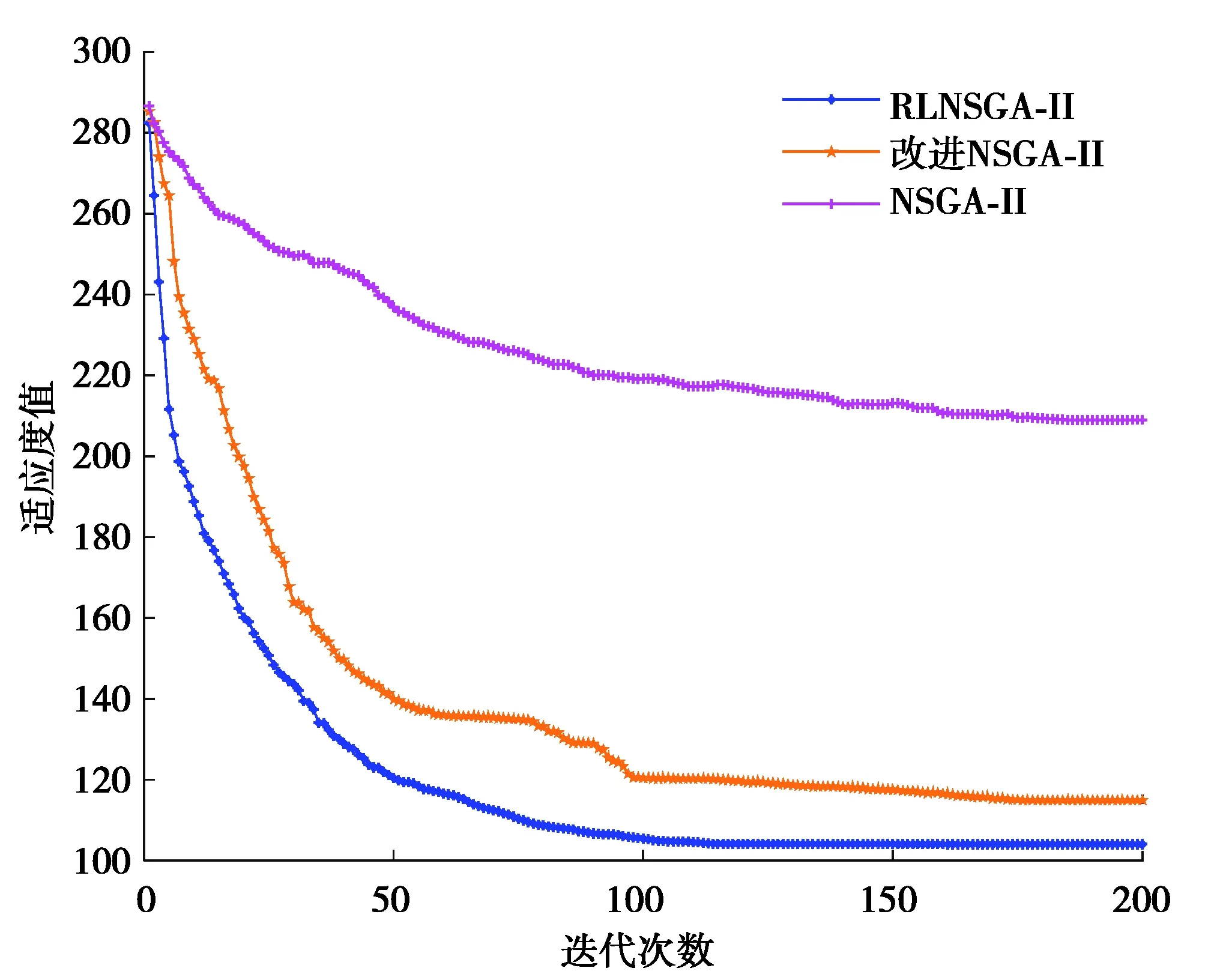
图7 算法收敛性对比Fig.7 Algorithm convergence comparison

由图7中收敛曲线对比分析可知，采用双种群进化策略改进NSGA-II后，可以明显提升算法的收敛速度，克服NSGA-II易于局部收敛问题。而RLNSGA-II同时引入双种群进化策略和强化学习机制，收敛速度更快，种群适应度值更优。验证了RLNSGA-II算法能够有效改善NSGA-II的收敛性能。

图8和图9分别为算法求解过程中两个多样性度量指标的变化曲线。由图8可知，采用强化学习对NSGA-II改进后，种群的解间距能够快速地降低并保持在较小的范围内，说明RLNSGA-II得到的解更加均匀。图9为熵度量值对比图，相比于NSGA-II和改进NSGA-II，RLNSGA-II在前100次迭代过程中可以更好地保持种群熵度量值在较大的范围；而在后100次迭代过程中，RLNSGA-II相比于改进NSGA-II在加快收敛的同时仍能有效保持熵度量值，增加解的离散性，验证了RLNSGA-II能够较好保持种群的多样性。

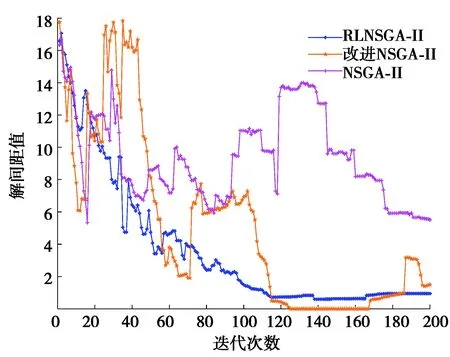
图8 解间距值对比Fig. 8 Comparison of solution spacing values

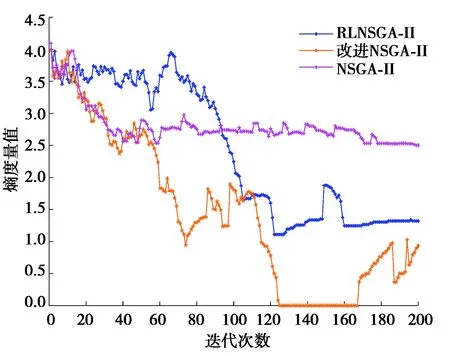
图9 熵度量值对比Fig. 9 Comparison of entropy measures

4 结束语

针对完工时间、机器总负荷和瓶颈机器负荷3个调度目标，提出了一种基于强化学习的改进NSGA-II算法求解MO-FJSP问题。运用性别判定法对种群进行拆分，并采用双种群进化策略改进NSGA-II的进化过程，增加算法局部搜索空间和全局搜索能力，改善收敛性能；根据种群解间距和熵值两个度量指标建立状态空间，通过强化学习机制调整种群比例参数，间接调整种群的进化方向，将种群多样性保持在合理范围内，避免了NSGA-II易于收敛至第一等级非支配曲面的缺陷。最后，通过仿真基准算例验证了算法求解的有效性和对NSGA-II改进的优越性。未来将继续对算法进行优化，进一步研究RLNSGA-II用于柔性作业车间多目标动态调度等复杂问题。