深水环境下压力补偿泵柱塞副的润滑特性分析

曹学鹏，鞠健阳，田富元，卫昌辰，丁 凯，王德硕，贺占瑞

(1.长安大学 工程机械学院机电液一体化研究所，西安 710064； 2.先进节能驱动技术教育部工程研究中心，成都 610031)

陆地资源枯竭迫使人类将目光投向了广袤的深海。随着“蛟龙号”“深海勇士”潜水器的相继问世，中国深海勘探技术取得了长足的进步，同时对深海领域液压传动技术提出更高的要求。斜盘式轴向柱塞泵凭借其功率密度大，在高压工况下，容积效率高等突出特点，成为目前深水环境下应用较为广泛的一类油压动力源，柱塞副作为其关键摩擦副之一，在深水环境下，柱塞副油膜的良好润滑性能是提高柱塞泵工作性能的关键。

研究的压力补偿式柱塞泵(压力补偿泵)位于薄壁油箱内，假定深水压力未超过泵体所能承受的容许值，不考虑壳体变形，且柱塞-缸体间压差不受水深变化影响。考虑深水环境下柱塞副油液介质属性变化，建立深水环境压力补偿泵柱塞副流体动力润滑模型，构建数值寻优求解方法，获得深水环境下柱塞副的膜厚、压力、间隙泄漏量及轴向摩擦力的变化规律，为深水环境下压力补偿泵摩擦副的性能分析和设计提供理论指导。

1 压力补偿泵柱塞副动力学分析

1.1 柱塞泵的深水压力补偿原理

深水环境下柱塞泵的压力补偿原理如图1所示，柱塞泵、深海电机、换向阀等元件浸入充满液压油的油箱中，油箱采用薄壁结构，外设有活塞式压力补偿器[13]。当水深变化时，海水压力、温度等环境参数通过压力补偿器和油箱壁面实时传至箱内液压介质和柱塞泵，始终保持箱体内外压力平衡，进而使液压泵工作在深海油压环境中，而执行元件则处在外界海水中。

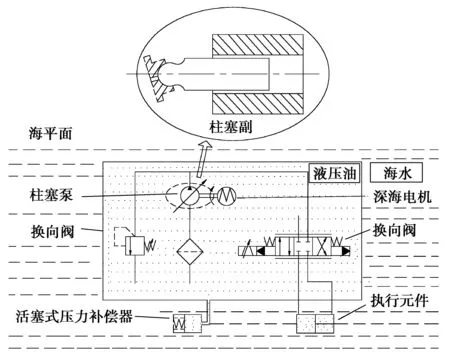
图1 深水环境下柱塞泵压力补偿原理图Fig. 1 Schematic diagram of pressure compensation of plunger pump in deep water environment

1.2 柱塞副的动力学分析

考虑上述工作环境，柱塞副润滑为完全流体动力润滑，在给定工况下，柱塞副的油膜厚度和相对压力分布同大气工况，均由外负载决定。柱塞运动主要包括3部分：自旋、轴向运动以及随泵体的旋转，图2所示为柱塞受力示意图。

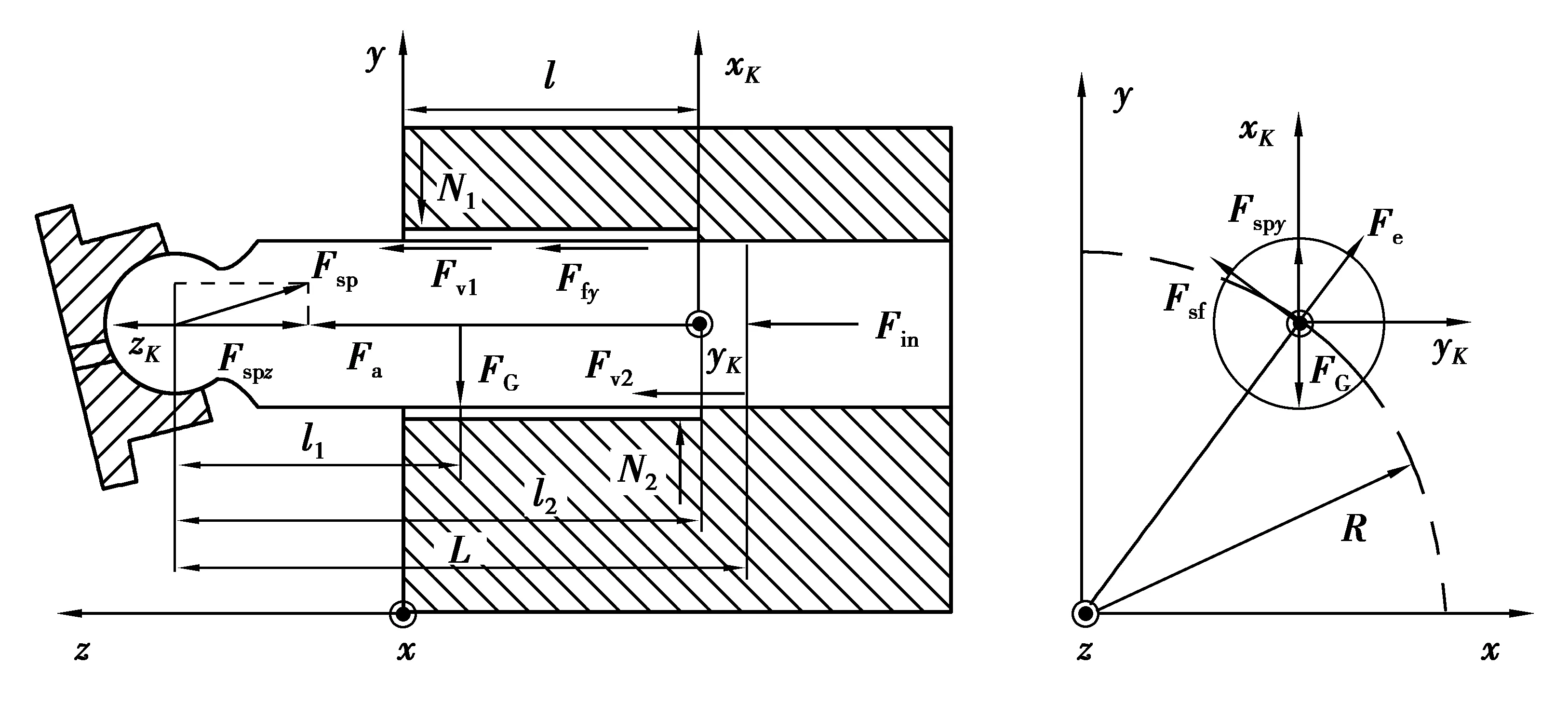
图2 柱塞受力示意图Fig. 2 Schematic diagram of plunger force

其中，l1、l2分别表示柱塞球心到质心和端面的距离，m；Fin为柱塞腔入口油液的压力，N；Fa为柱塞轴向往复运动惯性力，N；Ffx、Ffy分别为柱塞圆周和轴向运动引起的黏性摩擦力，N；N1、N2分别表示不同位置柱塞与缸体的固体接触力，N；Fv1、Fv2分别表示不同位置柱塞与缸体接触产生的滑动摩擦力，N；Fsp表示斜盘对柱塞的支撑力，N；Fsf表示柱塞球头滑靴所受摩擦力，N；FG表示柱塞自身重力，N；Fe表示柱塞绕主轴运动的离心力，N。

假定柱塞质心保持在自身轴线上，且不受滑靴旋转的影响，则柱塞轴向往复运动惯性力：

(1)

式中：ms、mp分别为滑靴和柱塞的质量，kg；a为轴向运动加速度，m/s2；ω为角速度，rad/s；R为柱塞的分布圆半径，m；β为斜盘倾角，(°)；φ为柱塞以上死点为参考的顺时针转过的角度，(°)。

在zk轴正方向上的合力：

Fspz=Fin+Fa+Ffy+Fv1+Fv2。

(2)

其中，Fv1=N1f，Fv2=N2f，f为柱塞和缸体间的摩擦系数。

柱塞球头端受到斜盘的支撑力可以沿z轴、y轴方向分解，其中沿z轴方向的分力为：

(3)

外力于xK和yK轴方向上的合力、合力矩分别为:

Fsx=Fecosφ+Fspsinβ-FG+Fsfsinφ，Fsy=Fesinφ-Fsfcosφ，

Msx=Fesinφ(l2-l1)-Fsfcosφl2，Msy=(FG-Fecosφ)(l2-l1)-(Fsfsinφ+Fspsinβ)l2。

(4)

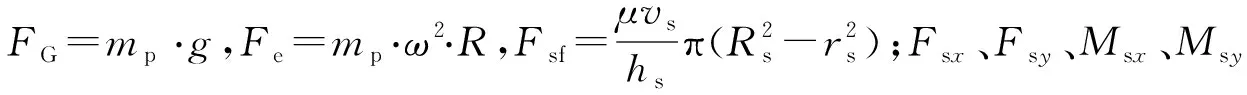
惯性力Fa和离心力Fe与柱塞宏观运动有关。柱塞在轴向力的驱动下沿缸孔的轴线往复运动。在径向力作用下，柱塞在缸孔径向上产生微运动。鉴于油膜的厚度为微米级，柱塞的径向加速度非常小，故忽略径向惯性力。油膜的压力用于平衡所有其他外力，柱塞的力与力矩平衡方程式为：

(5)

式中：Fpx、Fpy、Mpx、Mpy分别为沿xK、yK轴方向流体对柱塞的作用分力、力矩。

上述柱塞平衡方程为含有4个未知偏心变化e的非线性方程组。在不同位置和姿态，柱塞与缸体的接触间呈动态变化，故方程组(5)的求解实际上为有约束的非线性优化问题，即在给定角度位置φ处，需寻找一组偏心距E=[E1,E2,E3,E4]及相应的固体接触力，满足：

||ϑ(E)||≤ea，

(6)

式中ea表示求解精度，取10-6；当范数小于10-6认为柱塞已达平衡状态。

2 柱塞副流体动力润滑模型

2.1 柱塞副的油膜厚度模型

柱塞副在缸孔中的位置姿态，如图3(a)所示，通过柱塞轴线相对缸孔中心偏移值[e1,e2,e3,e4]来衡量其倾斜程度[14]。考虑到油膜厚度相对较小，可沿着缸孔轴线展开，如图3(b)所示。得到油膜展开前后坐标系的关系：

x=rpγ，y=zk，z=h(γ,zk)，

(7)

式中：rp为柱塞半径，m；γ为油膜上任意点的角度，(°)。

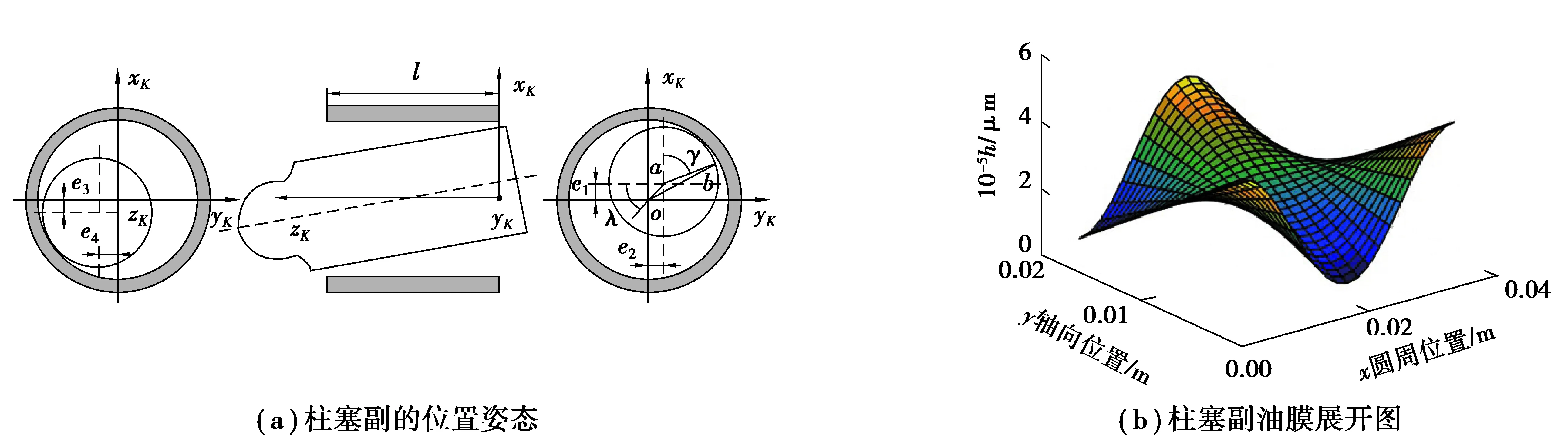
图3 柱塞在缸孔中的倾斜姿态Fig. 3 Inclined posture of plunger in cylinder bore

根据空间几何关系，可得油膜厚度h公式为：

(8)

式中：c为平均间隙，m；l为油膜长度，m。

2.2 柱塞副油膜的压力方程

2.2.1 深水环境下油液介质模型

参考文献[15]热带海域水温铅直向分布情况，可得环境参数如压力、温度随水深变化呈现如图4所示的变化。

图4 深水环境参数随水深的变化曲线Fig. 4 Dynamic change curve of pressure and temperature in deep water environment

当柱塞泵外部采用图1所示的带有压力补偿器的薄壁油箱结构时，环境压力、深水温度等通过油箱壁面影响泵内液压介质，引起工作介质属性的变化。根据已有研究成果获得了深水环境参数作用下的油液黏度、密度等介质特性变化规律[16]，分别表示为：

(9)

式中：K、B、C、a1、a2、b1、b2为黏度参数；T为环境温度，℃；P为压力，MPa。

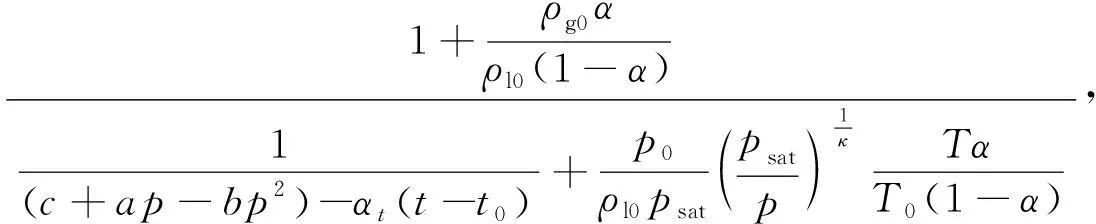
(10)

式中：a、b、c、αt为相应参数；ρ为油液密度，kg/m3；ρg0、ρl0分别表示标准状态下空气和纯油液的密度，kg/m3；α为油液含气率；t为油液温度，℃；t0、T0分别为初始油液温度和环境温度，℃；p0为大气压力，MPa；psat代表饱和状态时的压力，MPa；κ表示空气体积多变指数。式中各参数的取值如表1、2所示。

表1 深水环境下油液黏度模型中参数取值表[17]

表2 纯油液的密度方程中的参数取值表[17]

2.2.2 深水环境下柱塞副油膜压力方程

假定柱塞、缸体为刚性体，不考虑柱塞弹性变形及油膜厚度的影响。对柱塞副油膜的压力方程中，摩擦副表面的粗糙度小于最小油膜厚度，柱塞副间的油液是层流牛顿流体，同一水深下沿厚度方向压力、油液物理属性等保持不变，考虑不同水深下的油液介质属性变化，柱塞副的流体压力控制方程可表示为：

(11)

式中：vx为柱塞的自转速度，m/s；vy为柱塞轴向运动速度，m/s。

为提高数值结果的通用性和计算过程的稳定性，对压力偏微分方程量纲化：

(12)

式中ps为水下环境压力，MPa。

(13)

式中：ε=ρ*H3/μ*；μ*表示油液量纲为1的黏度，μ*(x,y)=μ(x,y)/μ0；ρ*表示油液量纲为1的密度，ρ*(x,y)=ρ(x,y)/ρ0。

3 柱塞副润滑模型的数值求解

3.1 油膜厚度的数值求解方法

油膜厚度的数值求解过程包括2个环节，即全斜盘转角位置下偏心值求解和全周期内柱塞副的油膜厚度分布的求解。

1)求解边界：当柱塞与缸孔中心线不重合，且偏离程度较大时，柱塞端部易与缸体内壁产生挤压，视柱塞与缸孔均为刚体，设两表面粗糙度均为Rz=0.05 μm，许用油膜厚度取[h]=0.1 μm。当柱塞副的油膜厚度达到[h]时，认为柱塞与缸孔发生局部接触摩擦。此时，油膜厚度保持[h]不变，偏心量最大。

2)全斜盘转角位置下偏心值的寻优及求解：

a.先求解某斜盘转角位置的油膜厚度分布，见公式(8)，采用坐标轮换法[18]迭代求解柱塞偏心距E，设其迭代初值:Eφ=[1,0,-1,0]。

b.由式(13)求柱塞副的油膜压力场，据数值积分求力与力矩FPX，FPY，MPX，MPY。令ϑ(E)=0，经式(5)变换后获得两端接触力：

(14)

c.对N1、N2进行迭代判断，交替使用黄金分割法进行一维搜索。

d.计算||ϑ(E)||，判断循环或进入下一角度位置计算，最后获得全转角位置下柱塞的偏心量。如图5所示为单个角度位置偏心量寻优求解流程图。

3)借助该偏心量计算全周期内柱塞副的油膜厚度分布，其求解流程如图6所示，设定的偏心量收敛条件为：

(15)

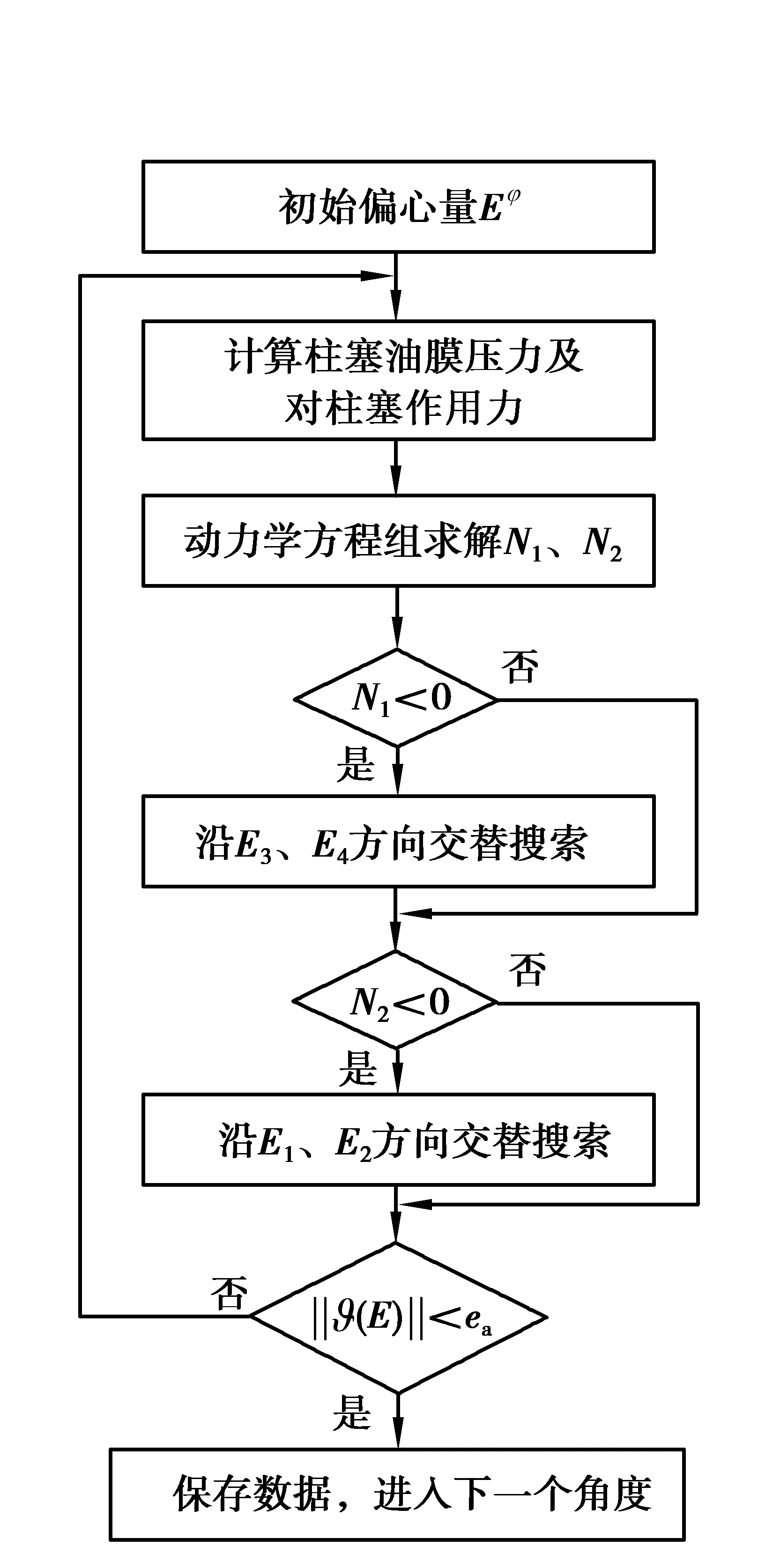
图5 单个角度位置偏心量寻优求解流程Fig. 5 Single angular position eccentricity optimization solution process

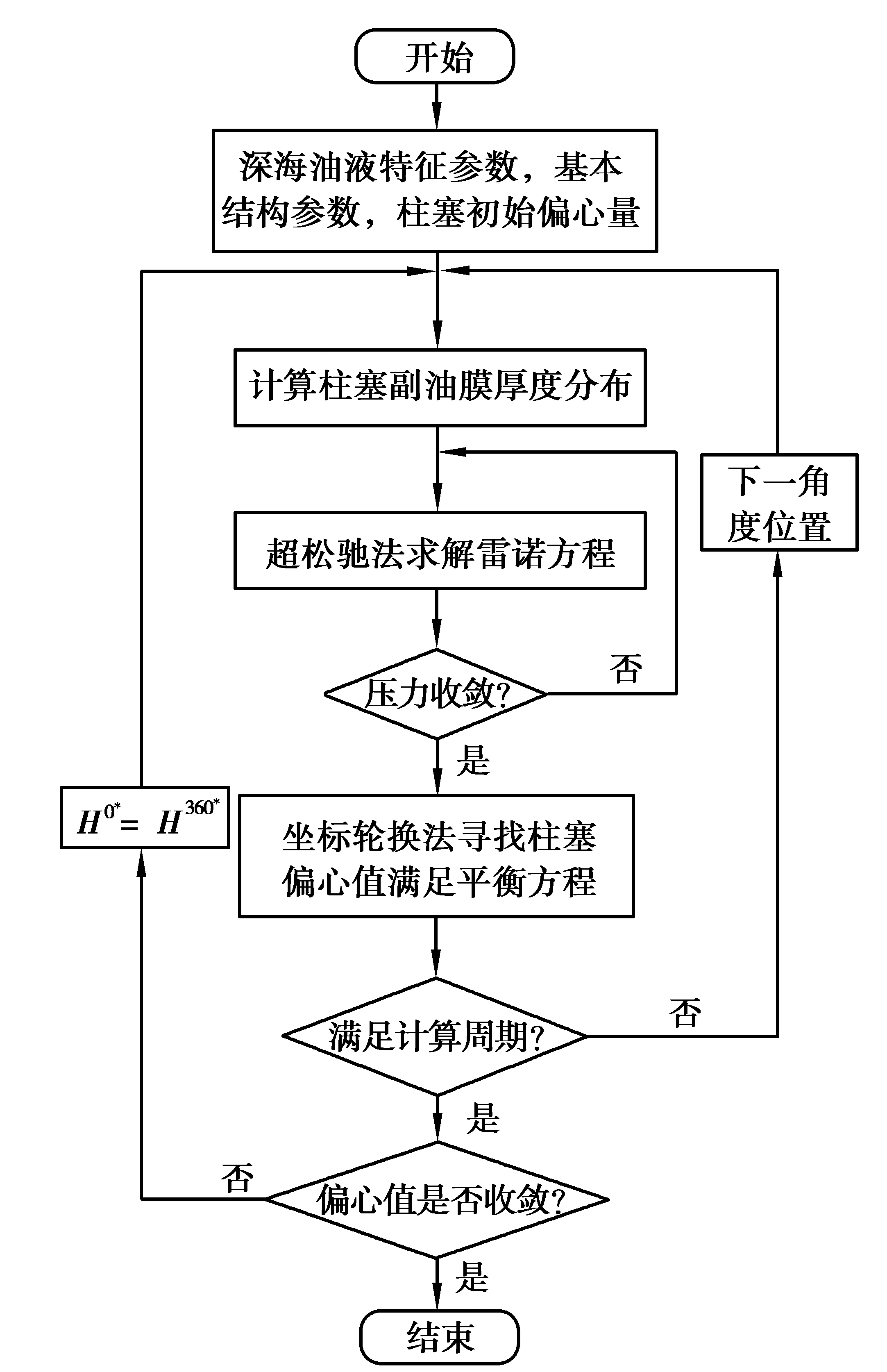
图6 深水环境下全周期内柱塞副油膜厚度的求解流程Fig. 6 The solution process of the plunger pair oil film in the full cycle in the deep sea environment

3.2 油膜压力分布的数值求解方法

由于压力方程式(13)为椭圆形偏微分方程，有效解析解通过常规计算较难求得，为此采用有限数值差分法[19-21]求解柱塞油膜压力。将流体计算域划分成若干等间距网格，如图7所示。

图7 流体域的网格划分Fig. 7 Mesh division of fluid domain

节点P(i,j)处一阶偏导数中心差分格式：

(16)

节点P(i,j)处二阶偏导数中心差分格式：

(17)

油膜挤压项的差分格式为：

(18)

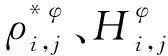
将式(16)～(17)代入到式(13)中，得到压力方程的差分格式为：

(19)

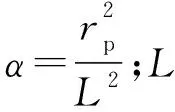
进一步整理压力求解可得：

(20)

利用加权求和的方法整理式(20)所得的压力与未修正压力，下一轮压力用此压力进行求解：

(21)

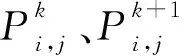
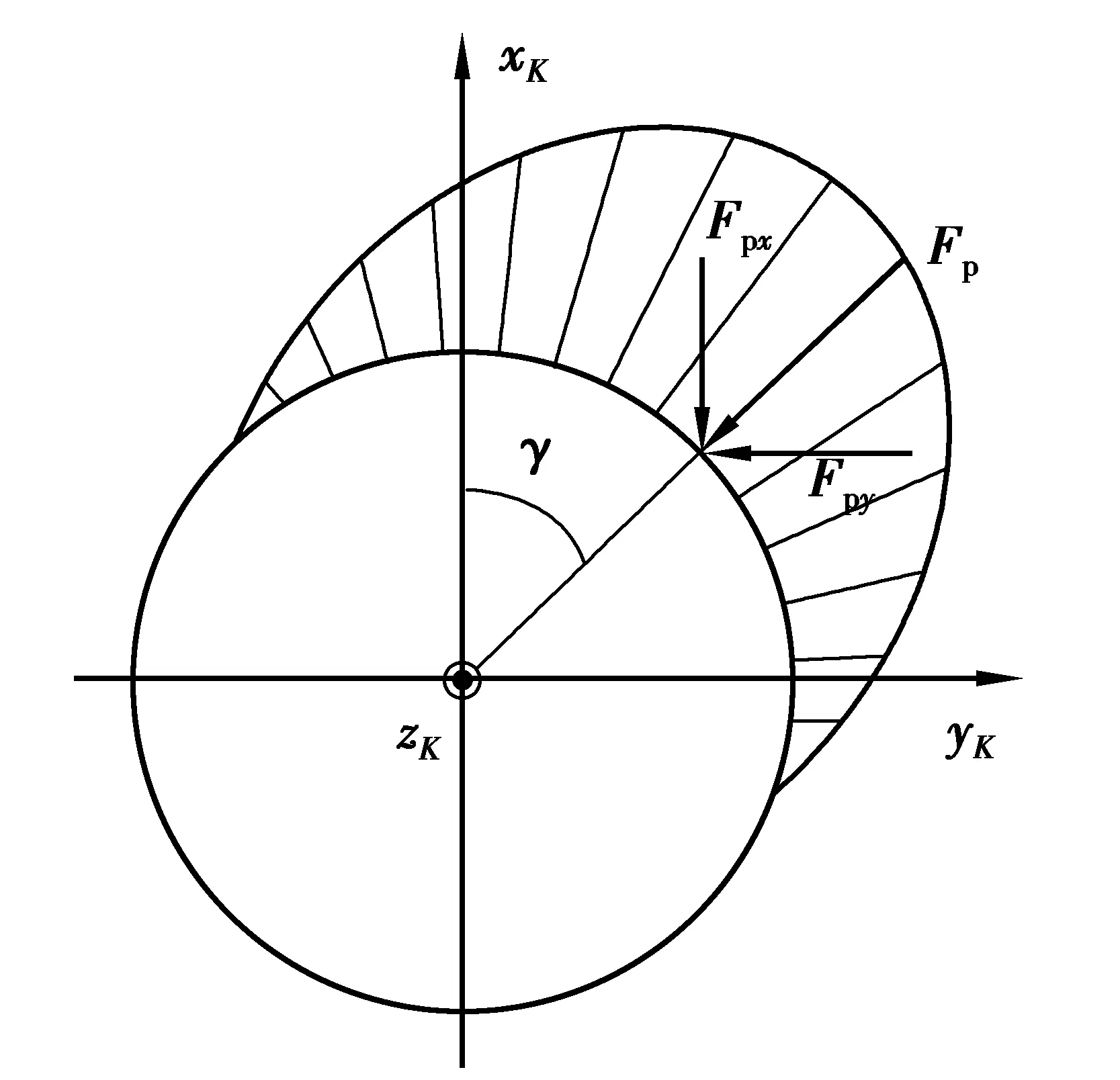
图8 柱塞副的油膜力作用示意图Fig. 8 Schematic diagram of oil film force action of plunger pair

压力迭代求解过程的结束条件：

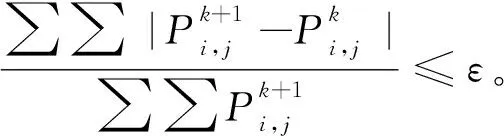
(22)

式中相对精度ε取10-6，此时各节点处压力分布即为柱塞副的压力分布。

运用数值积分方法求解柱塞副油膜作用力与力矩，如图8所示，其表达式为：

(23)

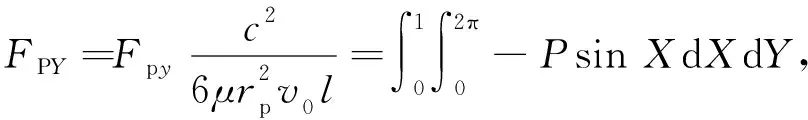
(24)

(25)

(26)

同理，可获得油膜对柱塞的轴向摩擦力及柱塞副间隙的泄漏量，分别表示为：

(27)

(28)

4 模型验证及数值分析

4.1 模型验证

通过与经实践验证的经典计算结果进行对比，以验证上述模型的有效性。设置与文献[2]相同的工况参数，即满足：

(29)

在柱塞不同转角下的模型求解，得油膜压力分布结果(图9(a)(b)下图)与文献[2](图9(a)(b)上图)的对比。可知，VY=-1时(图9(a)),球头端油膜压力峰值与偏心值成正相关，上、下两三维曲面所示的油膜的分布吻合度高；VY=1(图9(b))，油液入口处的油膜压力亦与偏心值成正相关，同样上、下两图曲面形貌和趋向亦接近一致，从而验证了本文所建模型及其求解流程的合理性及有效性。

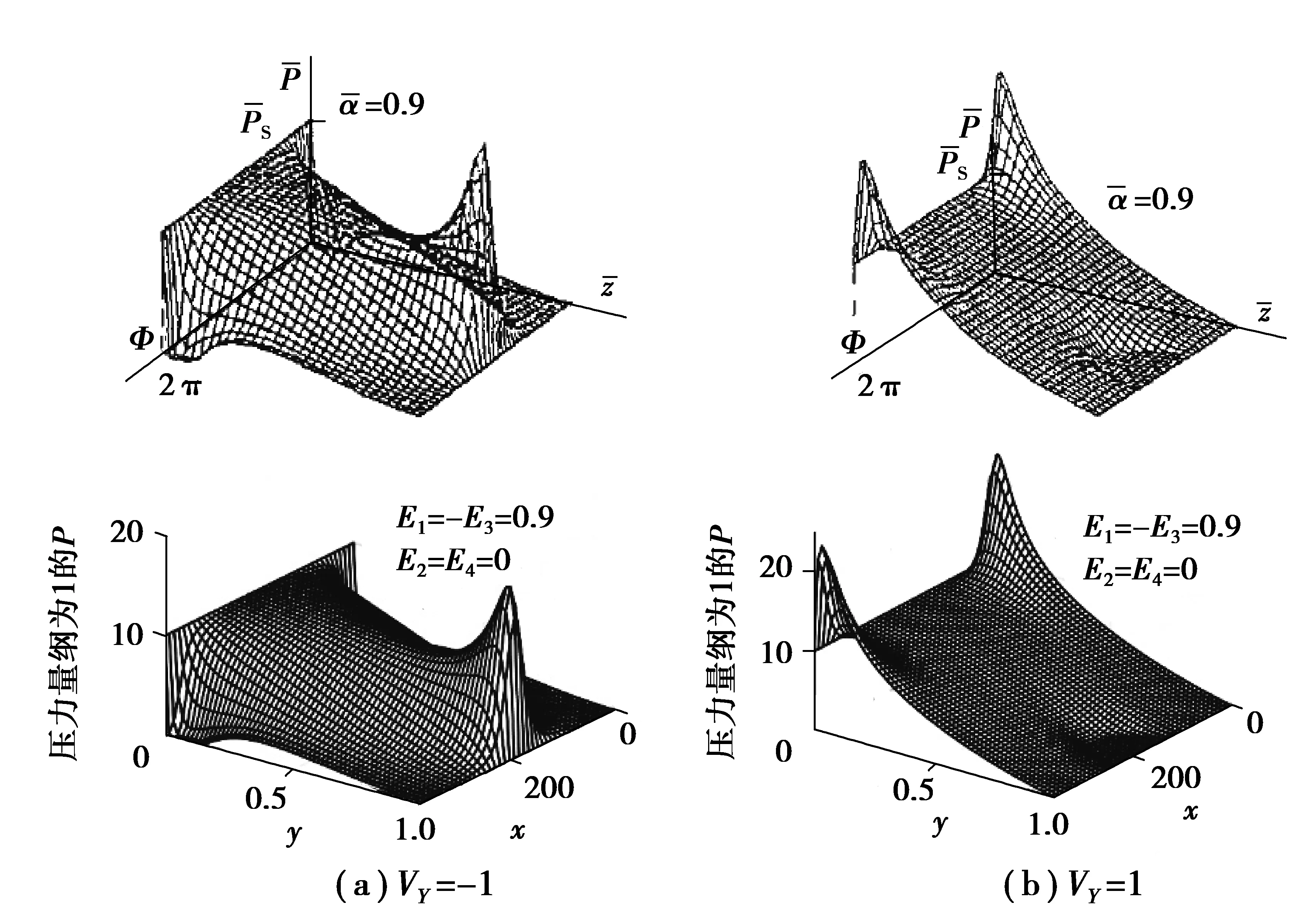
图9 油膜压力求解的结果对比图Fig. 9 Comparison of the solution results of oil film pressure

4.2 数值分析

4.2.1 定水深下的柱塞副润滑特性分析

根据图6所示的全周期内油膜厚度计算流程图编写相应程序，当结果收敛后将各角度下油膜厚度、压力等的分布输出。首先分析给定水深下的柱塞副油膜的润滑特性，初始计算参数如表3所示。设定柱塞轴向运动速度随主轴转角的变化如图10所示。

表3 柱塞副相关参数

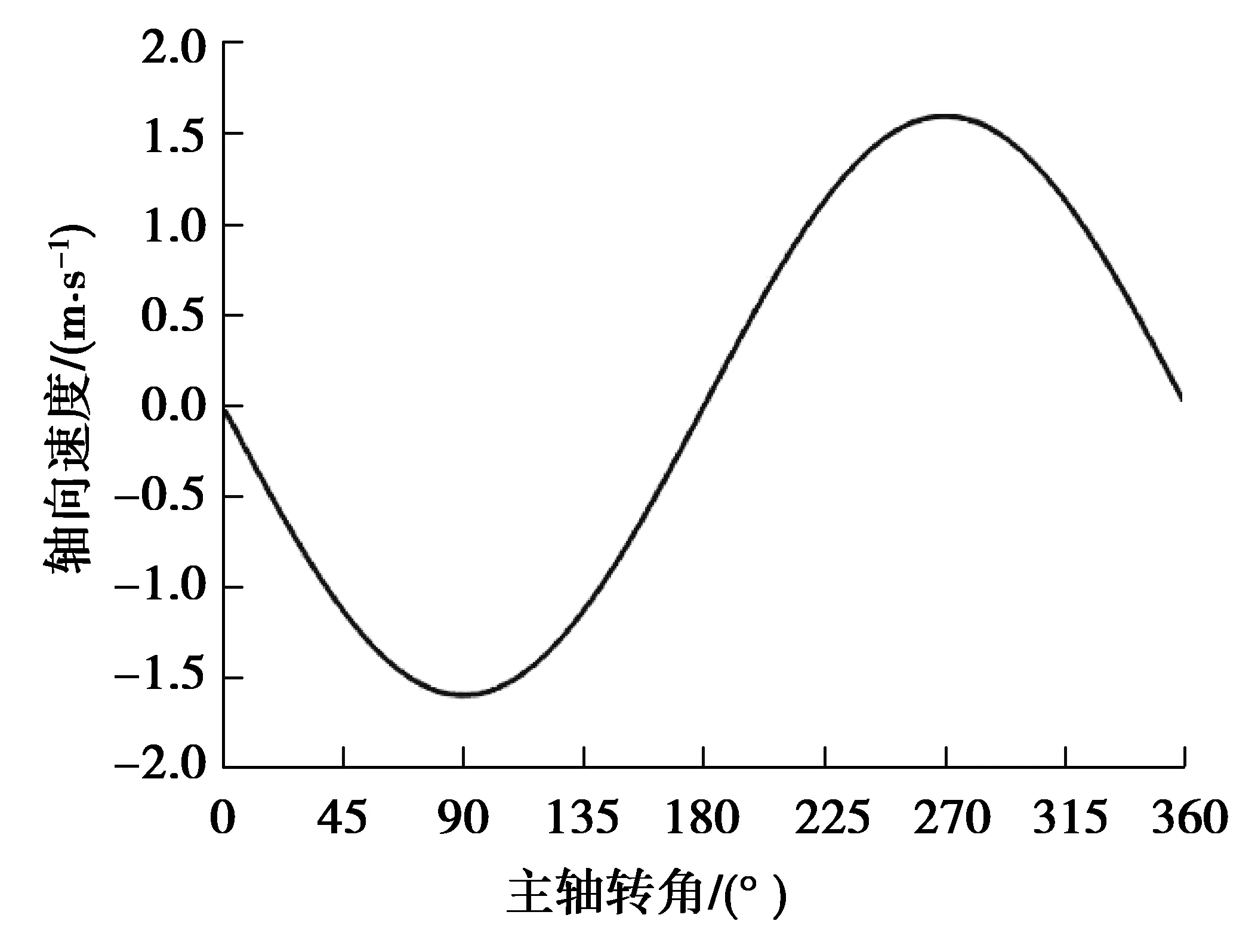
图10 柱塞轴向运动速度变化曲线Fig. 10 The changes of the axial movement speed of the plunger

设水深1 000 m，泵轴转速为1 500 r/min，工作压力为16 MPa，斜盘倾角12°，柱塞转角位置分别为2°, 30°,90°,182°，其油膜的厚度和压力分布如图11～12所示。

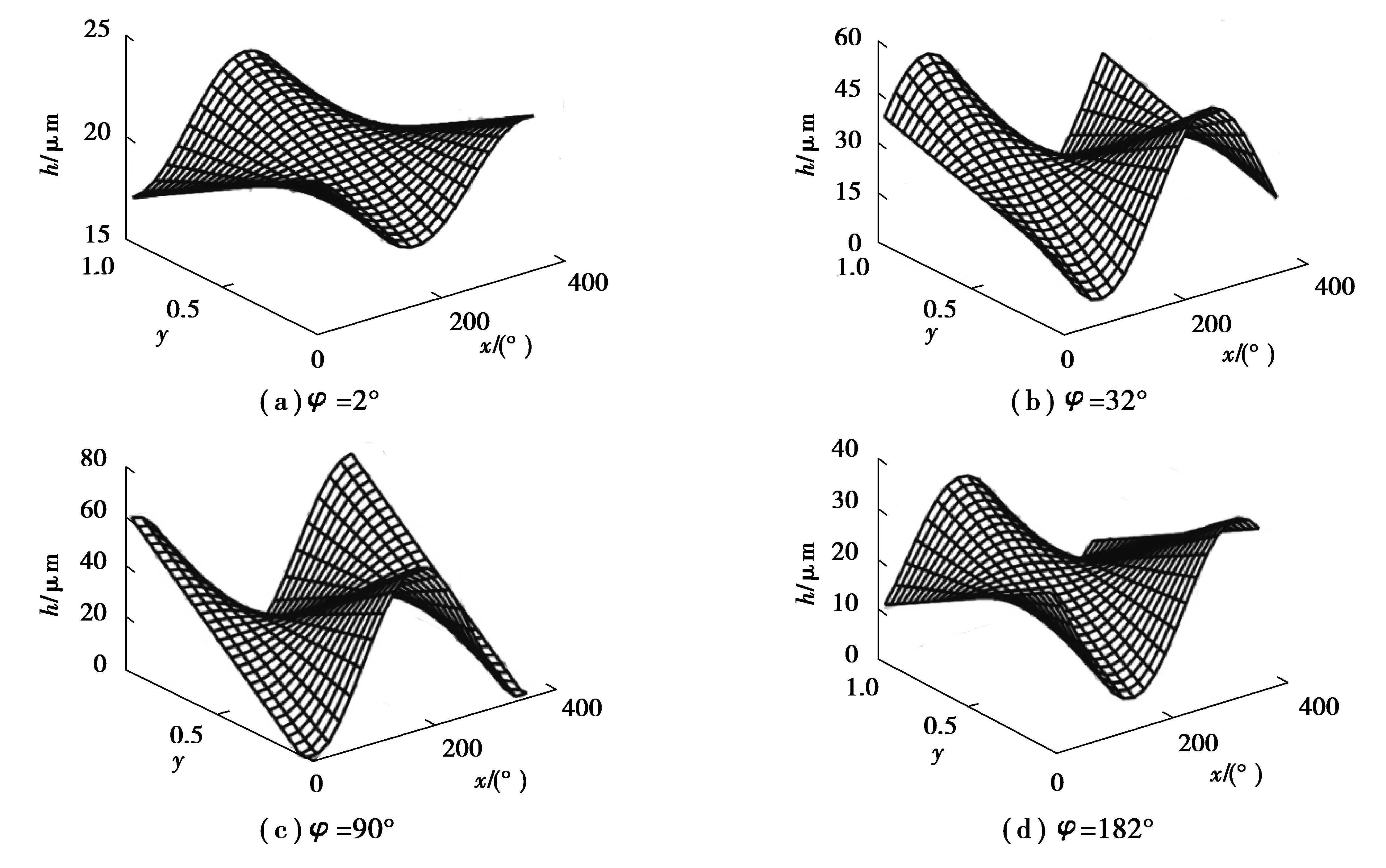
图11 水深1 000 m下不同转角时柱塞副的油膜厚度分布Fig. 11 Distribution of oil film thickness of plunger pair at different turning angles at a water depth of 1 000 m

图12 水深1 000 m下不同转角时柱塞副的油膜压力分布Fig. 12 Oil film pressure distribution of plunger pair at different rotation angles at a water depth of 1 000 m

水深1 000 m下不同转角时柱塞副的油膜压力、厚度变化如表4所示。当泵转角φ=90°时，油压最大峰值达到80 MPa，该位置柱塞偏心达极限，膜厚极薄，极有可能与缸体间发生固体接触。由以上图表可得，柱塞副的油膜压力分布与油膜厚度分布同步变化，油膜压力随着该处油膜厚度的减小而逐渐增大，但两分布的波动均随着柱塞偏载的增大而增大。在柱塞泵工作过程中，由于负载的时变性，柱塞需不断改变自身偏斜程度来动态平衡外负载。

表4 水深1 000 m下不同转角时柱塞副的油膜压力、厚度变化

不同水深下油膜厚度极差变化曲线如图13所示。在转角φ为0°～45°时，油膜厚度极差平稳上升，油膜厚度分布相对均匀；在转角φ=90°左右，油膜厚度极差达到最大值，该区域油膜厚度波动大，柱塞与缸体产生接触；在转角φ为135°～360°时，油膜厚度极差缓慢减小，油膜厚度恢复均匀分布。当水深增加时，油膜厚度整体波动更加剧烈，油膜厚度最大极差转角区间以φ=90°为中心向两边拓宽，柱塞产生固体接触的转角提前，接触转角范围扩大。

图13 不同水深下油膜厚度极差变化曲线Fig. 13 Variation curve of oil film thickness range under different water depths

水深1 000 m工况下在一个周期内柱塞副泄漏量变化曲线如图14所示。上死点是柱塞开始运动的起点，在起始状态柱塞做缩回运动，运动速度逐渐增大，整个过程泄漏量为正；随着运动速度继续增大，柱塞间隙慢慢开始吸收油液，泄漏量出现负值；转角φ=90°时，柱塞运动速度为反向最大，泄漏量最小；转角超过φ=180°后，柱塞进入低压区伸出吸油，运动方向与压力作用方向相同，泄漏量为正，但柱塞副两端压差较小，由于剪切流的作用，泄漏量呈与轴向速度相一致的正弦变化规律，转角φ=270°时，轴向速度达正向最大，泄漏量最大。

水深1 000 m工况下在一个周期内柱塞轴向摩擦力变化曲线如图15所示。在一个周期内高压区的轴向摩擦力数值相比于低压区的轴向摩擦力数值要大一些，这是因为在高压区柱塞两端压差较大，此时压差流的存在增大了黏性摩擦力。转角φ=90°时，轴向黏性摩擦力随柱塞轴向运动速度同步达到正向最大；在低压柱塞两端油压偏小，此时压差流的作用效果较小，剪切流主导黏性摩擦力的大小。转角φ=270°时，轴向黏性摩擦力达反向最大。

图14 水深1 000 m下柱塞副泄漏量变化曲线Fig. 14 Leakage curve of the plunger pair at a water depth of 1 000 m

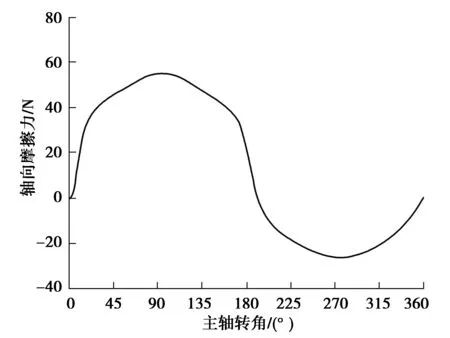
图15 水深1 000 m下柱塞副轴向摩擦力变化曲线Fig. 15 Variation curve of axial friction force of plunger pair in water depth of 1 000 m

4.2.2 变工况参数下柱塞副润滑特性分析

1)主轴转速的影响。在水深1 000 m，设定工作压力16 MPa，斜盘倾角15°，取泵主轴转速分别为1 000，1 500，2 000 r/min，缸体转动一个周期柱塞副泄漏量和轴向摩擦力的变化如图16所示。

图16 不同转速下柱塞副泄漏量和轴向摩擦力Fig. 16 Piston pair leakage and axial friction at different speeds

如图16(a)所示，泄漏量曲线变化随着主轴转速的提高而增大。在转角φ=0°～180°范围，柱塞做缩回运动，此时剪切流与压差流方向相反，随着主轴转速的增加，柱塞轴向速度和剪切流占比均增大，泄漏量会减小，甚至出现负值，即出现油液倒吸现象；在转角φ=180°～360°范围，柱塞做伸出运动，此时剪切流与压差流方向相同，主轴转速增加，泄漏量增大。随着主轴转速增加，柱塞副油液速度梯度增大，轴向摩擦力增加，如图16(b)所示，在高压区和低压区柱塞的运动方向相反，轴向摩擦力存在负值，在变转速工况下，高压区的摩擦力数值变化更为显著。

2)斜盘倾角的影响。在水深1 000 m，设定工作压力16 MPa，泵体转速1 500 r/min，取泵斜盘倾角分别为8°、12°、15°，一个周期内柱塞副油液泄漏量和轴向摩擦力的变化如图17(a)(b)所示。

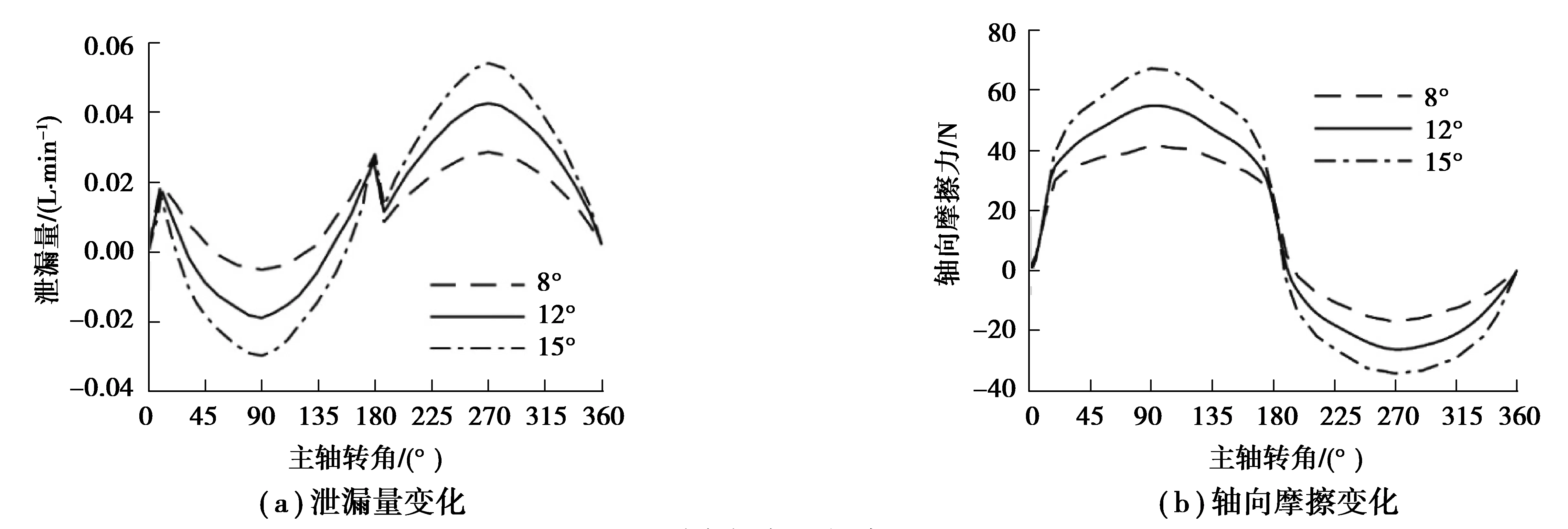
图17 不同斜盘倾角下柱塞副泄漏量和轴向摩擦力Fig. 17 Leakage and axial friction of the plunger pair at different swashplate inclination angles

如图17(a)所示，在高压排油区，倾角越大，柱塞副泄漏量越小，在低压吸油区则相反；如图17(b)所示，柱塞轴向摩擦力变化与斜盘倾角变化呈正相关；这是因为斜盘倾角增加使柱塞轴向往复运动行程、速度均增加，油液速度梯度增大，泄漏量和轴向摩擦都会增大。在一个周期内，斜盘倾角变化对总泄漏量影响较小，而轴向摩擦损失随着倾角的增大而增大。

3)变水深环境的影响。设定泵转速为1 500 r/min，工作压力16 MPa，斜盘倾角12°时，当工作水深分别为1 000，2 000，3 000 m时，一个周期内柱塞副油液泄漏量和轴向摩擦力的变化如图18(a)(b)所示。

图18 不同水深下柱塞副泄漏量和轴向摩擦力Fig. 18 Leakage and axial friction in different water depths

如图18(a)所示，水深增加，在高压区，间隙从泵体内吸油量增加，低压区，间隙向外泄漏油液减少，整个周期内柱塞副泄漏量减小；这是因为在压力补偿器的作用下，虽然水深增加，但柱塞副出入口的相对压力保持不变，即可保持轴向运动速度和压差不变，由式(9)可知，水深增加使油液黏度增加，导致泄漏量减小。如图18(b)所示，轴向摩擦力与水深成正相关变化，由式(10)可知，这是由于水深增加以后流体黏性增大，各节点上对应的切应力增大，从而使整个周期内的轴向摩擦力增加。由此可见，深水环境使柱塞副的容积效率提升，但机械效率下降。

5 结 论

1)考虑深水环境因素对液压介质黏度、密度等属性的影响，获得表征压力补偿泵柱塞副润滑特性的压力控制方程，与已有经实践验证的计算结果相吻合，表明建立的压力控制方程的有效性。

2)提出适应于深水工况柱塞副的油膜厚度和压力控制方程的求解方法和数值计算流程，获得表征柱塞副的油膜厚度、压力分布、泄漏量等润滑特性的变化规律，为深水环境下压力补偿泵摩擦副的性能分析和预测打下基础。

3)深水环境下的研究结果表明，在水深1 000 m，当柱塞泵转角90°左右，柱塞副的油膜压力达最大，此时柱塞偏载达极限，出现膜厚极薄区域，为油膜润滑的危险点。此外，随水深的增加，柱塞副的容积效率提升，但机械效率下降。