疲劳荷载对橡胶-钢纤维混凝土变形、能量及损伤性能的影响

刘家兴， 杨荣周， 徐颖,2*， 顾柯柯， 谢昊天

(1.安徽理工大学土木与建筑学院， 淮南 232001； 2.安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室， 淮南 232001)

随着中国经济社会发展不断深入，生态环境的地位和作用日益凸显，因此，国家越来越关注废弃物产生量高及其再处理的问题，如报废轮胎产生的橡胶废弃物等[1]。根据预测，全世界每年约有10亿个废旧轮胎在垃圾场堆积并处理(掩埋、焚烧等)[2]，这对生态环境产生的负面影响尤其令人担忧[3-4]。为了解决废旧轮胎带来的生态环境问题，许多研究人员持续在开发所谓的橡胶混凝土，来研究橡胶在混凝土中的应用[5-7]。

文献[8-9]通过试验分析发现，橡胶可以改善普通混凝土的疲劳性能，同时提高变形、抗冲击[10]和耐磨能力[7]，但减小了动态压缩比能量吸收值[11]；刘妙燕等[12]、徐颖等[13]对疲劳荷载下橡胶混凝土的损伤和断裂能进行分析，结果表明损伤因子呈倒S形规律变化，且断裂能与橡胶掺量有关；Yang等[14]、杨荣周等[15]对橡胶水泥砂浆进行动静态循环载荷试验，结果表明随着循环荷载等级的增大，试件的加载应变和累积残余应变均增大。文献[16-18]对纤维橡胶混凝土进行动静态试验，结果表明纤维和橡胶混掺时，其阻裂能力好。Alsaif等[19]、刘雨珊等[20]对纤维橡胶混凝土进行研究，结果表明掺入纤维可以提高橡胶混凝土的强度，同时又增强其峰后能量吸收的能力。Abdel等[21]通过试验分析发现，橡胶和钢纤维混掺可以提高循环荷载下梁柱节点的变形和耗能能力。赵秋红等[22]通过对纤维橡胶混凝土进行理论分析，提出了单轴循环受压应力-应变关系模型。综上所述，目前对橡胶混凝土和纤维橡胶混凝土已经进行了大量的试验研究，但较少对橡胶-钢纤维混凝土(rubber-steel fiber concrete，R-SFC)在静态压缩增幅循环加-卸载下的变形性能、能量特征以及损伤规律进行系统且全面的分析，且分别从变形和能量的角度定义损伤变量来衡量R-SFC的损伤程度的研究更鲜见报道。

为此，通过对3种橡胶粒径下4种橡胶取代率的R-SFC试件分别进行静态压缩增幅循环加-卸载试验，对其在试验过程中产生的应力-应变全曲线、变形、总输入能、弹性应变能和耗散能进行了系统且全面的分析。最后，基于变形和能量的分析过程，提出了累积残余应变损伤和能量耗散损伤，并讨论了循环次数、不同橡胶取代率和橡胶粒径对其的影响。

1 试验概况

1.1 原材料和配合比

水泥为普通硅酸盐水泥(P·O 52.5)；水为实验室自来水；粒径分别为0.85、2、4 mm的橡胶颗粒；钢纤维为端钩型，其长径比为46.7；减水剂为聚羧酸高强减水剂；Elkem940微细硅灰；密度和细度模数分别为2 600 kg/m3和2.40的河砂；R-SFC的配合比如表1所示，其中橡胶颗粒以等体积取代河砂的方式掺加，其取代率分别为0、10%、20%和30%(体积分数)；钢纤维采用外掺的方式，其体积率为2%。

1.2 试件设计和试验方法

以橡胶取代率和橡胶粒径为研究变量、钢纤维为研究定量，通过浇筑的方法，每组浇筑3个立方体试件(100 mm×100 mm×100 mm)，共计10组。24 h后脱模，将脱模的试件放在相对养护湿度大于90%、温度为(20±2) ℃的养护室内养护28 d。

本试验利用YAW-1 000 KN电液伺服万能试验机对立方体试件施加静态增幅循环压缩荷载；试验的加载方式以程序控制进行，其加、卸载速率均为1 500 N/s。试验测试方法为：以0～60 kN为第一个循环加-卸载区间，之后第i(i≥1)个循环加-卸载区间为0～60ikN，直至加-卸载到试件失稳破坏。

2 试验结果及其分析

2.1 R-SFC的变形性能

2.1.1 循环受压应力-应变全曲线

图1为各组试件在增幅循环加-卸载下的应力-应变全曲线。可以看出：①在加-卸载前期，加-卸载曲线相对紧密，应力退化微乎其微，在加-卸载中期，随着循环次数的增加，加-卸载曲线逐渐变疏，应力退化逐渐增加，且在某一次循环时，滞回环(加载曲线和卸载曲线形成的滞回环[23])突然增大，塑性变形突增，且R-SFC的增大量明显小于SFC，这充分说明橡胶颗粒具有良好的阻裂特性，在加-卸载后期，与SFC试件相比，R-SFC试件的能量耗散明显，主要体现在R-SFC试件受荷后形成的不闭合滞回环相对较大；②对于任意一个加-卸载循环区间，当应力水平较低时，加载曲线和卸载曲线非线性特征明显；随着应力水平的增加，加载曲线和卸载曲线呈现明显的线性特征；当第i次加载曲线与第i-1次卸载曲线形成公共点之后，加载曲线再次呈现非线性特征，且随着循环次数的增加，非线性特征更加明显；③橡胶颗粒对SFC的疲劳应力方面表现出明显的负效应，会降低SFC的力学性能(降低程度与橡胶取代率成正比)，究其原因是掺加的橡胶颗粒弹模低，从而致使SFC的承载能力减小；④SFC试件在破坏后卸载曲线出现陡降，而R-SFC试件在破坏后卸载曲线更加缓和，应力退化更加平缓，耗能能力更加显著。

表1 试验混凝土配合比Table 1 Test concrete mix ratio

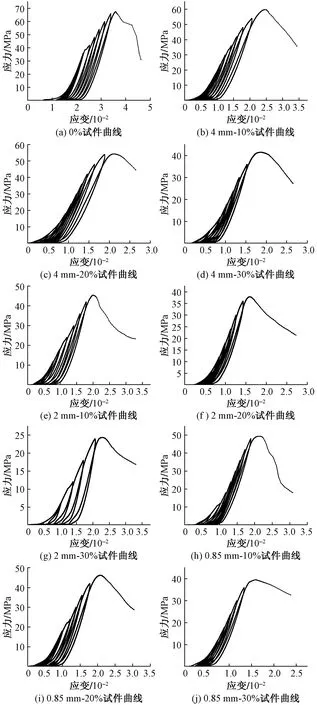
以4 mm-10%为例，表示橡胶粒径及其取代率分别为4 mm和10%图1 各组试件的单轴循环受压应力-应变全曲线Fig.1 Uniaxial cyclic compressive stress-strain curves of each group of specimens

2.1.2 不闭合度

各组试件的不闭合度与循环次数的关系如图2所示，不闭合度为相应的第i次循环加-卸载完成产生的应变。可以看出，随着循环次数的增加，不闭合度总体上呈现先减小后趋于稳定再增大的“三阶段”变化，值得注意的是在循环加-卸载后期，SFC的不闭合度值明显大于R-SFC。也就是说各组试件在第一次循环加-卸载完成后就产生了不可逆变形(初始缺陷快速发育阶段)；之后微裂隙平稳发展，于是不闭合度也逐渐趋于稳定，且此阶段占整个加-卸载过程的大部分；到循环加-卸载后期，损伤持续累积，导致各试件的不闭合度均快速地增加，但由于橡胶颗粒和钢纤维具有正向协同阻裂的能力，且在试件开裂后，协同的优势越加突出，故在循环后期R-SFC的不闭合度值明显小于SFC。

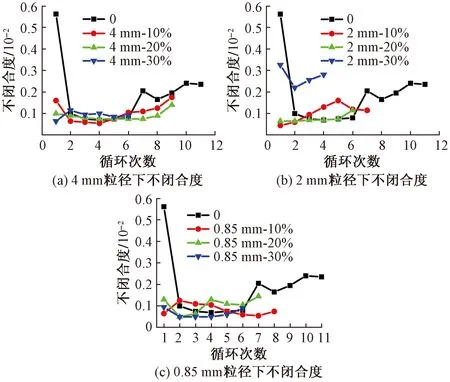
图2 不闭合度与循环次数的关系Fig.2 Relationship between the unclosed degree and the number of cycles

2.1.3 加、卸载变形模量

图3给出了各组试件的加、卸载变形模量与循环次数的关系曲线。加载变形模量、卸载变形模量计算公式分别为[15]

(1)

(2)

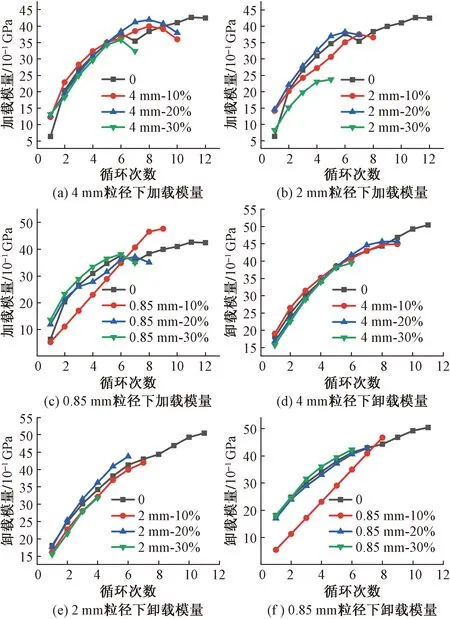
图3 加、卸载变形模量与循环次数的关系Fig.3 Relationship between the loading and unloading deformation modulus and the number of cycles

式中：EL为第i次循环加载完成时起点和终点之间的割线模量；EU为第i次循环卸载完成时起点和终点之间的割线模量；σOi、σAi和σBi分别为第i次循环的初始加载应力、卸载起始应力和卸载完成应力；εOi、εAi和εBi分别为第i次循环相应应力对应的应变。

由图3可知，加载变形模量、卸载变形模量均随循环次数的增加而逐渐增大，然而在试件临近破坏的一两次循环时，加载变形模量的增长速率开始逐渐减小，甚至出现了负增长，其本质在于损伤在循环前期的过程中逐渐累积增大，从而很大程度上削弱了试件的原有承载力，故在循环后期加载变形模量减小。通过对比加、卸载变形模量，可以发现在整个循环加-卸载过程中，卸载变形模量均大于相应的加载变形模量，究其原因是试件在第i次加载完成后，对试件内部造成了非结构性压密损伤，从而产生了不可恢复的压密变形，但此时试件并没有产生结构性损伤，反而压密变形使得每次循环卸载变形比加载变形小，因此卸载变形模量大于相应的加载变形模量。

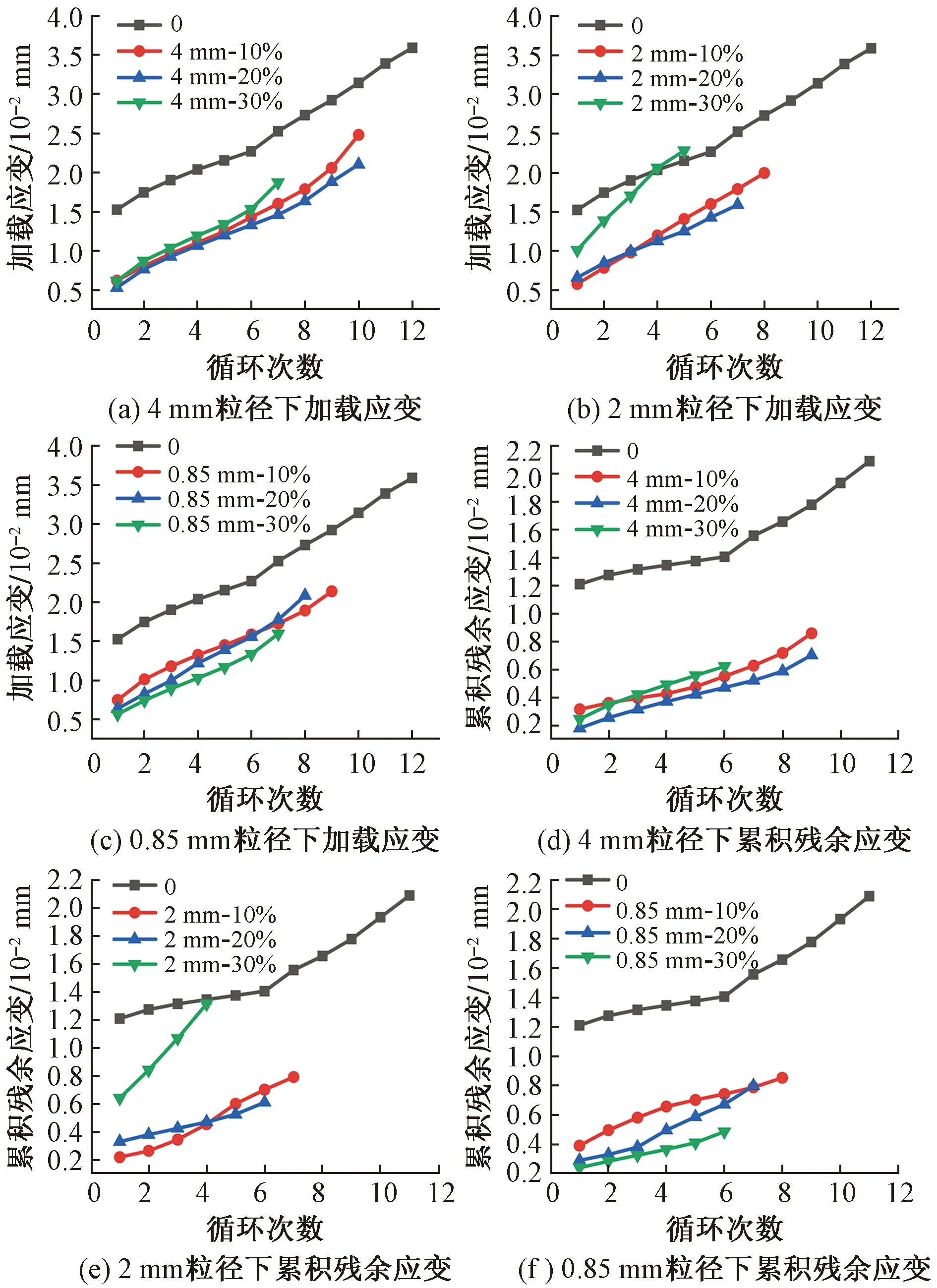
图4 加载应变、累积残余应变与循环次数的关系Fig.4 Relationship between loading strain, cumulative residual strain and number of cycles

2.1.4 加载应变、累积残余应变

各组试件的加载应变、累积残余应变与循环次数的关系如图4所示，加载应变为从初始加载原点到第i次循环加载的最大加载值的过程引起的应变，累积残余应变为从初始加载原点到第i次循环卸载的最小卸载值的过程引起的应变[24]。由图4可知，加载应变、累积残余应变均随循环次数的增加而增大，且SFC试件的加载应变和累积残余应变均明显大于R-SFC试件；在橡胶取代率相同时，对于仁意一次循环，SFC试件与R-SFC试件之间的加载应变差值和累积残余应变差值与橡胶取代率或橡胶粒径的变化无明显规律。以上说明橡胶颗粒和钢纤维协同逐级多层次耗能，从而减弱了基体破裂耗能，因此R-SFC试件发生的变形小，但是由于循环荷载区间逐渐增大，变形依然会增大。

2.2 R-SFC的能量特征

混凝土的疲劳破坏是能量反复驱动下的一种状态失稳。因此，为了更深入地探究R-SFC在增幅循环加-卸载下的疲劳性能，对其在试验过程中产生的总输入能、弹性应变能和耗散能进行了以下分析。根据热力学定律，在增幅循环加-卸载下，试件第i次加-卸载下的总输入能、弹性应变能、耗散能计算公式为

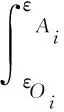
(3)

(4)

(5)

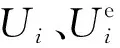
2.2.1 R-SFC的总输入能、弹性应变能

图5分别给出了各组试件的总输入能、弹性应变能与循环次数的关系曲线。可以看出，3种橡胶粒径下试件的总输入能速率、弹性应变能速率均随着循环次数的增加而增大，且在低次循环时，其增长速率基本相同，而在高次循环时，其增长速率出现了显著的不同。在整个循环加-卸载过程中，试件的总输入能都大于弹性应变能，且二者的差值随循环次数的增加而逐渐增大。与橡胶取代率为0%的试件的弹性应变能相比，其余3种橡胶取代率的试件的弹性应变能均较小。

综上分析，在低次循环时，虽然循环加-卸载区间逐渐增大(增幅)，各试件基本上仍处于弹性阶段前期，因此各试件产生的变形都较小，但是试件内部的孔隙和橡胶颗粒与基体相互摩擦错动的过程依旧会消耗小部分能量；在高次循环时，各试件产生

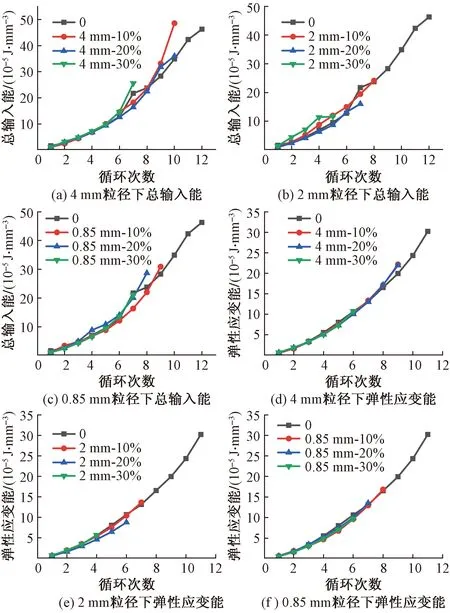
图5 总输入能、弹性应变能与循环次数的关系Fig.5 Relationship between total input energy, elastic strain energy and the number of cycles

了不同程度的损伤，许多能量主要以裂纹表面能、塑性应变能和孔隙贯通能耗散释放；而且低弹模的橡胶颗粒取代高弹模的骨料，会使试件强度降低，同时弱化了试件的储能机制[25]。

2.2.2 R-SFC的耗散能

图6给出了各组试件的耗散能与循环次数的关系曲线。可以看出，随着循环次数的增加，各试件的耗散能在低次循环时增长速率缓慢，在高次循环时，其增长速率较快，且3种粒径下R-SFC的耗散能基本上都大于SFC的耗散能。与橡胶取代率为0%的试件相比，其在第7次循环时，耗散能突增，而在之后的循环，耗散能先降低再二次增加，曲线增长不稳定；反观橡胶取代率为10%、20%和30%的试件，其耗散能增长曲线相对稳定。

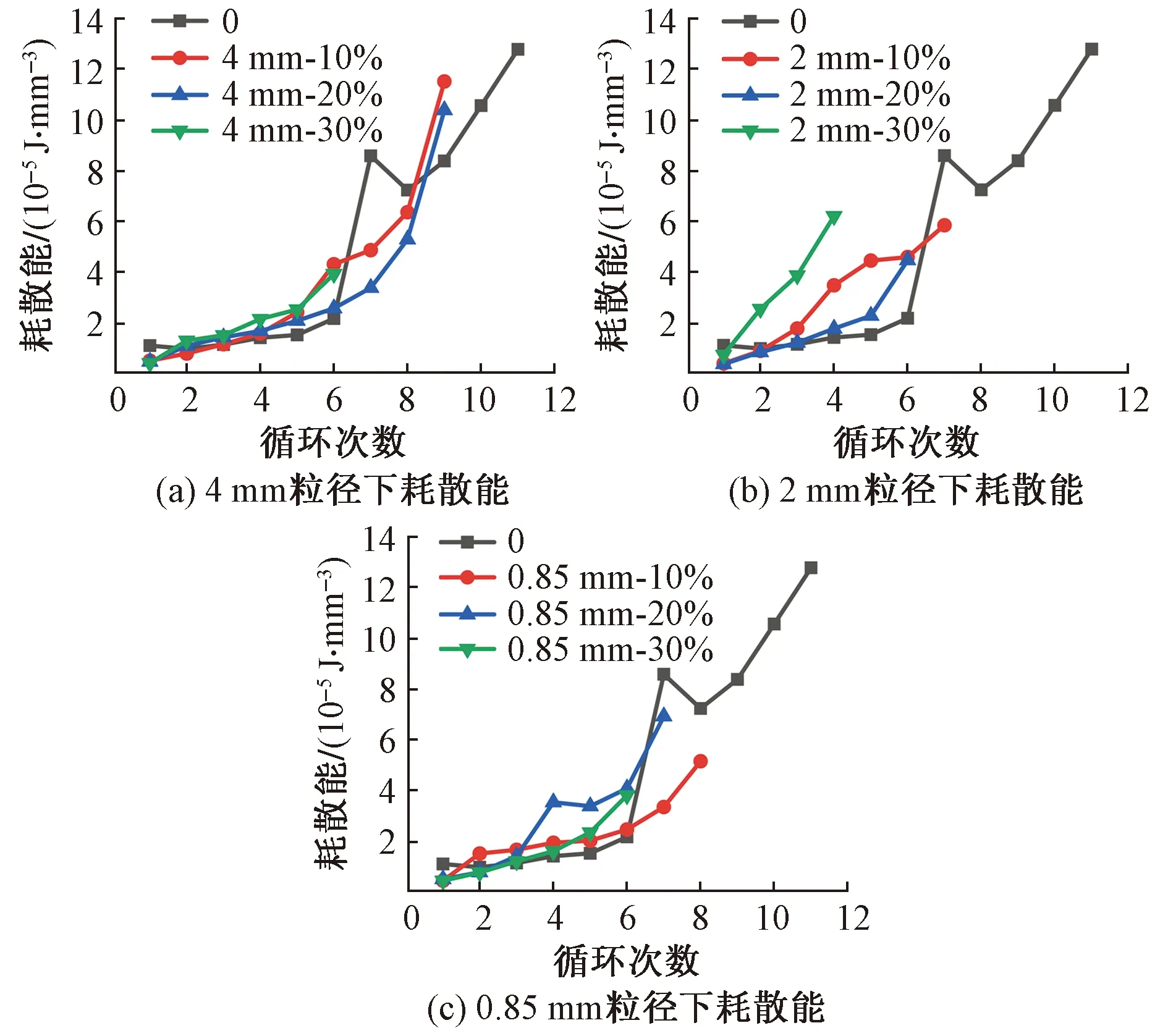
图6 耗散能与循环次数的关系Fig.6 Relationship between the dissipative energy and the number of cycles

综上分析，对于SFC和R-SFC在循环加-卸载过程中，相同点是在循环加-卸载前期，外载对试件几乎未造成明显的损伤，因此总输入能大部分转化为弹性应变能，储能机制占主导作用，故耗散能增加缓慢；在循环加-卸载后期，试件在循环加-卸载的作用下损伤逐渐累积，导致裂隙开始萌生、搭接、甚至贯通，该过程会持续消耗输入能，故耗散能开始快速增大。不同点是橡胶颗粒在循环加-卸载过程中会以自身发生弹性变形的形式消耗输入能，也就是说相比于SFC，R-SFC增添了新的耗能单元(橡胶)，故R-SFC的耗能能力优于SFC。

2.3 R-SFC的疲劳损伤

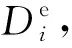
(6)

(7)

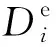
2.3.1 累积残余应变损伤

各组试件的累积残余应变损伤与循环次数的关系如图7所示。可以看出：①3种粒径下4种橡胶取代率的累积残余应变损伤均随着循环次数的增加而逐渐增大，且R-SFC的累积残余应变损伤增长速率微大于SFC，其本质在于循环次数的增加同时伴随着循环荷载的增大，以及低弹模的橡胶颗粒会降低R-SFC的强度，这就导致了R-SFC的累积残余应变损伤增长速率较快；②对于任意一次循环，除了橡胶粒径为2 mm、橡胶取代率为30%的一组试件，SFC的损伤值明显大于R-SFC的损伤值，且二者的差值随循环次数的增加而逐渐减小，减小量尤其以橡胶粒径为2 mm和0.85 mm明显，说明掺加橡胶颗粒可以强化SFC的阻裂能力，并降低其损伤程度，究其原因是橡胶颗粒以弹性应变能的形式储存消耗部分输入能[25]，同时橡胶颗粒与水泥基体形成的薄弱面更易滋生小裂隙，这就使试件内更多的钢纤维参与阻裂，从而充分发挥钢纤维的拉结耗能，因此可用于试件破裂的能量得到了有效地减弱，故R-SFC的损伤值小；③R-SFC的损伤值与橡胶取代率的增加和橡胶粒径的减小之间无明显的规律，但R-SFC的累积损伤增长速率表现出随橡胶取代率的增加而增大，由此可以看出增幅循环加-卸载下累积残余应变损伤增长速率与试件的强度有关。

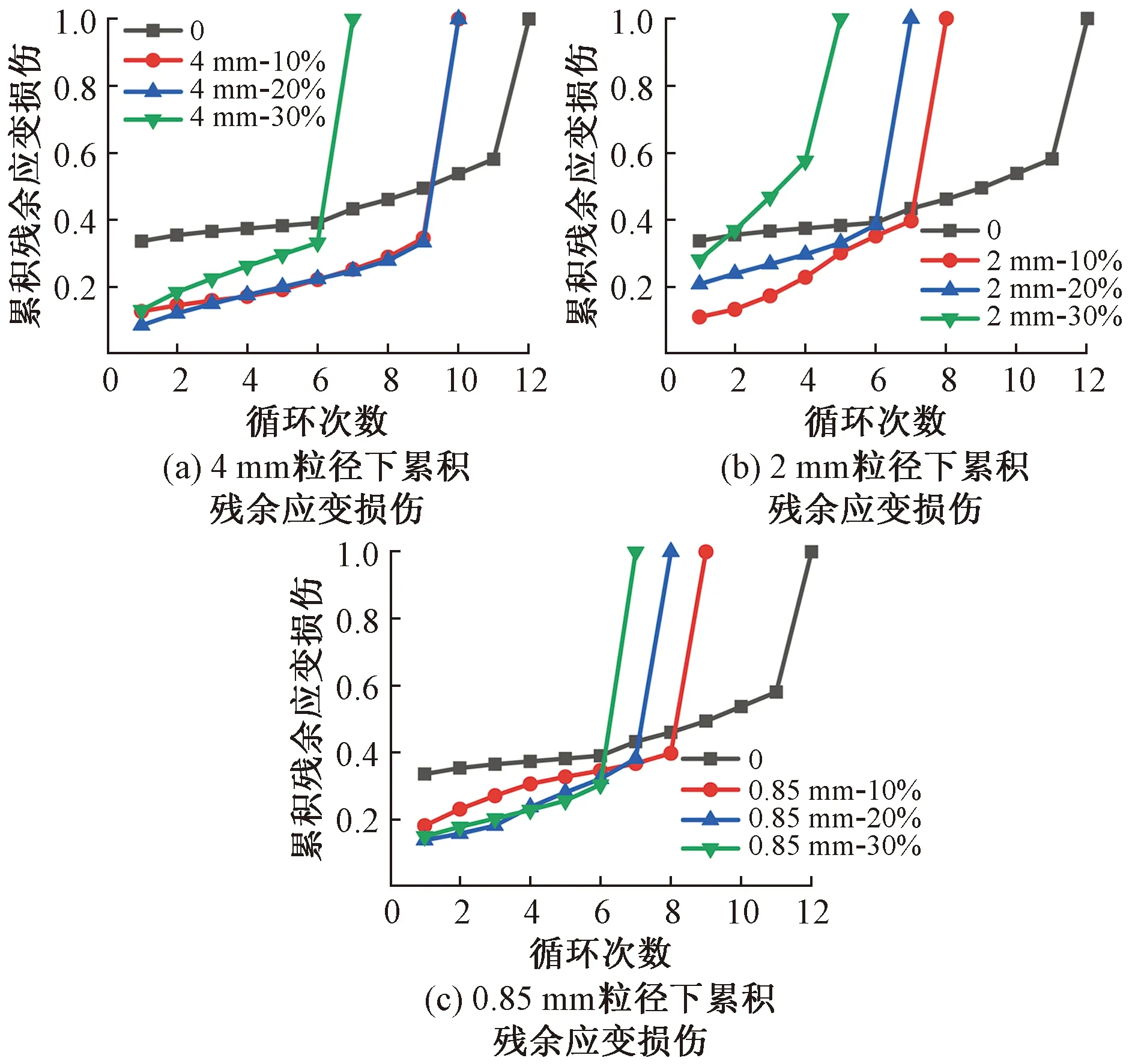
图7 累积残余应变损伤与循环次数的关系Fig.7 Relationship between the cumulative residual strain damage and the number of cycles

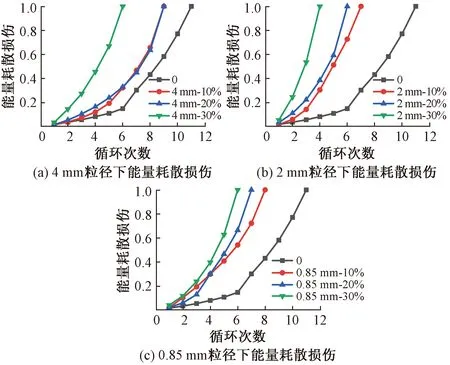
图8 能量耗散损伤与循环次数的关系Fig.8 Relationship between energy dissipation damage and the number of cycles

2.3.2 能量耗散损伤

图8给出了各组试件的能量耗散损伤与循环次数的关系。可以看出，在第一次加-卸载完成后，各组试件的内部就已经产生了不同程度的细微损伤；至第6次循环结束前，SFC的能量耗散损伤速率增加较慢，而R-SFC的能量耗散损伤速率增加相对较快；之后随着循环次数的增加，各组试件的损伤速率均迅速增加。对于任意一种粒径，随着橡胶取代率的增加，能量耗散损伤逐渐增大，且相邻橡胶取代率间的损伤的增大幅度随橡胶取代率的增加而逐渐增大，这说明能量耗散损伤增长速率与橡胶取代率有关，其本质以在耗散能小节赘述，这里不再重复解释。

3 结论

(1)在增幅循环加-卸载作用下，试件的应力-应变全曲线呈现先密后疏的“两阶段”变化，而不闭合度则呈现先减小后趋于稳定再增大的“三阶段”变化；其加、卸载变形模量、加载应变和累积残余应变均随着循环次数的增加而增大，且卸载变形模量大于相应的加载变形模量，而SFC的加载应变和累积残余应变大于R-SFC。

(2)在增幅循环加-卸载作用下，总输入能和弹性应变能均随着循环次数的增加而迅速增大，且R-SFC的弹性应变能小于SFC的弹性应变能，而耗散能则随着循环次数的增加先缓慢增大后迅速增大，且R-SFC的耗散能大于SFC的耗散能。

(3)对比累积残余应变和耗散能定义的损伤变量，随着循环次数的增加，两种损伤变量均逐渐增大，且R-SFC的两种损伤变量的增长速率均大于SFC；而随着橡胶取代率的增加，能量耗散损伤相邻橡胶取代率间的损伤的增大幅度逐渐增大，而累积残余应变损伤则与橡胶取代率的变化无明显规律。