混凝土裂纹扩展的非线性超声表征试验研究

聂智超, 连磊, 李绍令, 韩阳, 周荣武, 刘现鹏*

(1.交通运输部天津水运工程科学研究所港口水工建筑技术国家工程试验室, 天津 300456； 2.重庆交通大学水工建筑物健康诊断技术 重庆市高校工程研究中心, 重庆 400074； 3.长江宜昌航道工程局, 宜昌 443000； 4.浙江鸿海工程勘察设计有限公司, 温州 325000)

混凝土材料具有显著的固有非线性特征，即使对于制作工艺良好的构件，其内部亦包含大量微裂纹和微孔隙等初始损伤[1]。已有研究表明，传统超声检测技术对混凝土微损伤敏感性较低，无法用于损伤萌发和演化过程的检测与表征[2-3]，近年来新兴的非线性超声检测技术对材料微观结构的变化极为敏感，同时具有高效、便捷的优点，可作为超声检测技术体系的良好补充[4-6]。

常用的非线性超声检测方法包括高次谐波法、边带峰值计数法、非线性混频法等。陈军等[7]基于高次谐波法，利用嵌入式传感器对混凝土受压、钢筋混凝土梁受弯形成的损伤进行了非线性超声检测，证明了高次谐波法具有表征混凝土微观结构变化的能力。Nie等[8]、Zhao等[9]基于高次谐波法对含半贯通裂纹混凝土立方试样进行了超声扫描，探究了激励幅值、裂纹角度等因素对高次谐波产生的影响规律，提出了基于EEMD-小波的联合去噪技术，提取了更为精确的基波和二次谐波幅值。文献[10-12]验证了非线性超声技术对混凝土微损伤的敏感性，探究了水泥基材料在循环加载、硅-碱反应和外加剂作用下的非线性超声规律。Bompan等[13]通过加载引入混凝土损伤，利用线性和非线性超声方法对其进行检测与表征。许颖等[14-15]利用边带峰值计数法检测砂浆和混凝土试样微裂纹，获得了水灰比增大将导致非线性超声指标增大的结论。郑丹等[16]对高温条件下的混凝土非线性参数变化规律进行了研究，讨论了非线性超声检测方法表征混凝土宏观损伤的适用性。Liu等[17]利用非线性混频技术检测不同传播距离下的混凝土累积损伤，并与高次谐波法进行了对比，获得非线性混频技术对混凝土微损伤敏感程度更高的结论。

综上所述，现有混凝土非线性超声试验侧重于验证该技术对混凝土初始损伤的敏感性，鲜有混凝土微裂纹萌生-裂纹扩展-材料失效全过程的非线性超声响应规律研究，且混凝土非线性超声试验样本不足。为此，基于高次谐波法对混凝土的裂纹萌生与扩展过程进行了检测与表征，结合应力-应变曲线探究了不同加载水平下的非线性参数β变化规律，对比首波幅值与非线性超声参数，进一步讨论线性与非线性超声参数在表征混凝土裂纹演化过程的优势与不足。

1 非线性超声基本理论

假设一列纵波在固体介质内传播，将应力-应变关系扩展至二阶，代入一维波动方程，则该非线性波动方程的解u(x,t)可表示为[7, 9]

u(x,t)=u0(x,t)+u1(x,t)

=A1cos(kx-ωt)+A2cos(2kx-2ωt)

(1)

式(1)中：u0(x,t)为解u(x,t)的线性部分；u1(x,t)为解u(x,t)的非线性部分；x为质点位移；t为时间；k=ω/cL为波数，其中，ω为入射波角频率，cL为纵波波速;A1为基波幅值;A2为二次谐波幅值，其表达式为

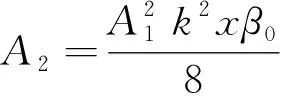
(2)

式(2)中：β0为二阶非线性参数。

则基波、二次谐波与非线性参数β0的关系可表示为

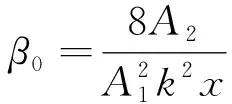
(3)

由于质点的绝对位移测量较为复杂，非线性超声试验中采用相对非线性参数β代替β0，则β的表达式为

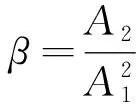
(4)

非线性参数β不仅与材料损伤程度有关，还取决于超声波传播距离和波束大小。经计算，受压过程中的混凝土最大侧向位移约为2 mm，由此引起的试样长度变化率仅为1.3%，故可忽略位移变化对非线性参数β的贡献。此外，试验过程中激励信号的频率保持不变，则k为常数。

2 单轴受压下的混凝土非线性超声测试

2.1 试样制备与养护

本试验共计制作4组混凝土试样，试样的几何尺寸为150 mm×150 mm×150 mm，配合比设计参照《普通混凝土配合比设计规程》(JGJ 55—2011)，混凝土配合比及抗压强度如表1所示。混凝土的制作使用重庆小南海水泥厂生产的42.5型普通硅酸盐水泥，粗骨料的最大粒径为20 mm。浇筑完成后，将混凝土试样放置在振动台上振捣15 s，然后覆盖聚乙烯塑料薄膜静置24 h等待脱模，成型后将混凝土试样移至Ca(OH)2饱和溶液中养护，养护时间为28 d。

表1 混凝土试样配合比

2.2 混凝土单轴受压测试

采用液压式压力试验机(DYE-2000型)对混凝土试样进行单轴加载，仪器可提供的最大荷载为 2 000 kN。加载前利用千分表检查混凝土试样的平整情况，确保承压接触面无明显高度误差，再将试样放置在承压板中心，打开送油阀门使上、下承压板与试样表面发生接触。混凝土单轴加载前，进行 20 kN 预压以保证承压钢板与试样表面紧密接触，接着关闭回油阀并打开送油阀，逐渐增大压缩荷载，期间控制平均加载速率为0.6 kN/s，直至试样完全破坏。

混凝土应变测量采用数显千分表，千分表量程为12.7 mm，通过磁力杠杆支架固定，固定完成后观察千分表读数5 min以保证其安装的稳定性。加载过程中记录上、下承压板位移，据此计算混凝土轴向应变。为获取更为准确的应力-应变曲线，荷载为0～200 kN加密位移采集的频次，间隔10 kN记录上、下千分表数值；当荷载大于200 kN，记录间隔为50 kN；当混凝土试样表面能够观察到裂纹，间隔 20 kN 记录千分表数值。

2.3 非线性超声测试

图1 受压条件下的混凝土非线性超声测试Fig.1 Nonlinear ultrasonic testing of concrete under uniaxial compression

图1(a)和图1(b)分别为受压条件下的混凝土非线性超声系统示意图及测试现场。试验采用Rigol 1022 U信号发生器发射10个周期的脉冲波，频率为40 kHz。由于信号幅值较高时会引起更强烈的超声波非线性特征，利用高压信号放大器ATA-2042将输出信号放大至200 V。发射与接收端分别采用 PXR 04型和PXR 07型接触式平面纵波换能器，换能器的频率响应曲线如图2所示，在基波频率f0=40 kHz和二次谐波频率2f0=80 kHz附近，换能器的灵敏度均大于60 dB，表明其具有良好的信号发射与接收效果。示波器型号为Tektronix 1072B，采样频率为50 MHz，满足Nyquist-Shannon采样定理。换能器安装时将发射与接收换能器完全对齐，试样与换能器间使用凡士林耦合并通过松紧带缠绕固定。选取接收信号中连续7个稳定波形做快速傅里叶变换获得频谱曲线，进而计算非线性参数β，典型的测试信号时、频域曲线如图3所示。

单轴加载过程中的超声信号采集方式与位移采集方式类似：当荷载低于200 kN，采用加密方式采集信号，采集间隔为10 kN；当荷载大于200 kN，采集信号间隔为30 kN；当混凝土表面出现裂纹，信号采集间隔调整为20 kN。在超声信号采集过程中，需要保证所接收波形处于稳定状态，对于临近失效的混凝土试样，其内部裂纹迅速扩展，示波器难以捕捉到稳定的波形，此时超声测试结果无意义，故停止超声信号的采集。

图2 发射与接收换能器频率响应曲线Fig.2 Frequency response curves of transmitting and receiving transducers

图3 典型超声信号时、频域曲线Fig.3 Typical time and frequency domain curves of ultrasonic signals

3 结果与讨论

3.1 混凝土试样微观形貌

在4个混凝土试样中任选一个进行扫描电子显微镜(scanning electron microscopy, SEM)试验，观察其微观结构以确保受压前无显著缺陷。为了避免电子积聚或样品表面的充电效应，试验前将自然断裂的两个薄片样品进行喷金处理。

如图4(a)所示，集料颗粒被界面过渡区(interfacial transition zone, ITZ)和砂浆基质紧密包裹，而ITZ被认为是混凝土内的薄弱区域。此外，在微观尺度下未观察到混凝土内存在显著的空隙和裂纹等损伤。微观尺度下的砂浆基质形貌如图4(b)所示，即使对于颗粒组分相对均匀的砂浆材料，仍能够观察到一定程度的随机性和不连续性，证明了非线性是混凝土材料的固有特征。鉴于微观尺度未发现明显的损伤，且试样的抗压强度高于设计强度，故可认为试验使用的混凝土试样制作工艺良好。

图4 典型超声信号时、频域曲线Fig.4 SEM micrographs of the concrete with a magnification of 400 times

3.2 加载过程中的非线性参数变化规律

为便于对比和分析，将应力σ、应变ε和非线性参数β进行归一化处理。图5为3个混凝土试样的σn-βn曲线与σn-εn曲线，其中，σn为应力σ与峰值应力σ0之比，βn为非线性参数β与峰值非线性参数β0之比，εn为应变ε与峰值应变ε0之比。受压过程中混凝土非线性参数变化可划分为P1、P2和P3阶段，P1阶段非线性参数比β/β0随着荷载增加逐渐增大，此时的应力水平较低，混凝土试样处于压密阶段和早期的弹性变形阶段；随着外部荷载增加，P2阶段非线性参数比β/β0由极大值迅速下降，混凝土试样仍处于弹性变形阶段；随着荷载继续增大，P3阶段非线性参数比β/β0呈显著波动变化趋势，直至无法接收到稳定波形，该规律发生于混凝土的弹性变形后期和塑性变形阶段。

线性与非线性超声参数在表征混凝土裂纹演化过程中具有较大差异。利用线性超声参数对混凝土结构进行检测，当混凝土裂纹未发生不稳定扩展或尚未达到临界应力时，波速、衰减等声学参数保持相对稳定状态[18-19]，相比之下，非线性超声参数对混凝土准弹性(30%～40%极限抗压强度)阶段具有良好的表征效果，故非线性超声技术能够弥补线性超声检测技术精度较低的缺陷。

3.3 裂纹扩展与非线性参数的关系

试验结果表明，非线性参数β的变化与混凝土内裂纹萌生与扩展存在密切联系，单轴受压下的裂纹扩展规律如图6所示[20]。当压缩荷载低于混凝土裂纹的起裂应力，试样内部水平方向微裂纹和微孔隙逐渐闭合，同时产生新的竖向微裂纹，故加载初期非线性参数β逐渐增大；随着应力水平的继续增加，水泥基质与骨料周围的应力集中效应愈加明显，内部应力达到微裂纹的起裂应力后，裂纹发生稳定扩展，此时超声波的吸收、散射等作用对基波和高次谐波存在较大干扰，非线性参数β迅速下降；随后裂纹发生非稳定扩展，其演化速度和方向均具有明显随机性，非线性参数β呈波动变化的趋势。

图5 混凝土的应力-非线性参数与应力-应变曲线对比Fig.5 Comparison of stress-nonlinear parameters and stress-strain curves of concrete

图6 单轴受压下的混凝土应力-应变曲线与裂纹扩展示意图Fig.6 Typical stress-strain graphs of concrete under uniaxial compression and its relation to (micro-) cracking

图7 受压破坏混凝土试样裂纹分布Fig.7 Distribution of crack in concrete after compressive failure

研究表明，非线性超声技术对材料损伤初期敏感性较强，非线性参数β随着材料微损伤的积累逐渐增大，当混凝土内的损伤达到一定规模，非线性超声效应反而显著降低[6,21]。受压破坏后的混凝土表面裂纹分布情况如图7所示，可以看出，受压过程中混凝土表面裂纹的出现与扩展具有较强随机性。此外，非线性超声测试中发现，当换能器周围微裂纹数量增多，接收到的信号稳定性明显下降，非线性参数β的波动程度显著增加。

综上分析，随着压缩荷载的增加，混凝土内的微裂纹数目增多，从而引起非线性参数β增大；当原先孤立的微裂纹发展成一个更为广泛和连续的裂缝体系，超声波在裂纹界面处发生显著的吸收、散射等效应，非线性参数β迅速下降；随着应力水平继续增加，裂纹发生不稳定扩展，非线性参数β随之波动变化。非线性超声参数具有表征混凝土结构微损伤的能力，然而实际工程中的混凝土构件往往排布钢筋，导致超声波在材料内部的传播异常复杂，对钢筋混凝土的非线性超声相关研究却鲜有报道[22]，需在后续研究中进一步补充和完善。

3.4 基于线性与非线性超声的损伤表征

对接收信号首波幅值A进行归一化处理，并与βn-σn曲线进行对比，结果如图8所示。P1阶段声波振幅An略有下降，对应的非线性参数比β/β0显著增大，最大首波幅值比A/Amax的平均变化率为26%，其中Amax为单轴加载过程中的最大幅值。非线性参数比β/β0的平均变化率为452%，说明利用超声波的衰减特性表征混凝土初始损伤的敏感性较低，而高次谐波法对混凝土微观结构的变化极为敏感。随着外部荷载进一步增加，混凝土损伤逐渐积累和扩展，其表面能够观察到多条裂纹，此时最大首波幅值比A/Amax显著降低，而非线性参数比β/β0先减小随后发生波动变化，反映了当混凝土出现较严重损伤时最大首波幅值比的表征效果更好。

微裂纹在混凝土内萌生与扩展过程中，最大首波幅值比A/Amax变化较小，而非线性参数比β/β0显著增加；当裂纹由微观扩展至宏观尺度，超声波在裂纹处发生的反射、吸收、散射等作用不可忽略，此时A/Amax显著减小，非线性参数比β/β0则发生波动变化。因此，在后续研究中建议联合线性与非线性超声方法共同表征混凝土损伤，在实际工程中既能提高检测的精度和灵敏度，又能够保证检测效果的稳定性和可靠性。

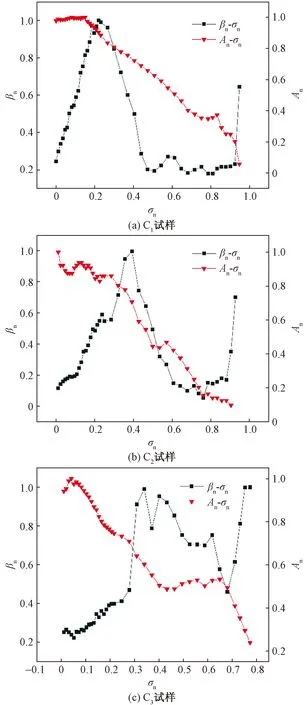
An为归一化首波幅值图8 最大振幅比和非线性参数随荷载的变化关系Fig.8 Relation between the maximum amplitude ratio and nonlinear parameters with the load increasing

4 结论

通过压缩荷载引起混凝土裂纹萌生和扩展直至试样破坏，在此过程中探究了非线性参数β变化规律，并结合线性声学参数讨论了高次谐波法表征混凝土宏观损伤的适用性和有效性，得出如下主要结论。

(1)加载初期β迅速增大，该现象对应于混凝土压密和弹性变形阶段早期；随后β显著下降，该过程仍出现在混凝土弹性阶段；随后非线性参数β波动变化，该过程对应于混凝土弹性阶段后期及塑性阶段。

(2)当外部荷载低于裂纹起裂应力，微裂纹逐渐积累与演化，非线性参数β显著增加；随着裂纹开始扩展，非线性参数β发生下降，并呈波动变化趋势，直至混凝土试样完全破坏。

(3)微裂纹萌生与演化初期非线性参数β最大变化率达452%，而首波幅值An的最大变化率仅为26%；随后非线性参数β下降并波动变化，而首波幅值An下降趋势明显，故非线性参数更适用于混凝土微观损伤表征，而首波幅值表征宏观损伤效果较好。