山区输电塔滚石撞击响应分析及撞击力计算

汪峰， 唐现梓， 黄伟

(1.三峡大学防灾减灾湖北省重点实验室， 宜昌 443002; 2.三峡大学土木与建筑学院， 宜昌 443002)

输电塔是电网系统的重要基础设施，输电线路穿越复杂山区和不良地质区域时，输电塔极易受到侧方滚石撞击，会造成输电塔结构破损和倒塌事故，严重时危及线路的运营安全。如2016年7月，四川凉山州西昌地区遭遇暴雨侵袭，境内500 kV普洪二线51号塔受到滚石冲击，破损严重。2019年8月，四川甘洛县山体滑坡，滚石导致该区域35 kV的高压输电线路多座铁塔倒塌，阿兹觉变电站被迫跳闸断电。

目前，针对滚石撞击及输电塔防护安全问题，中外学者开展了广泛的研究。王学良等[1]针对山区输变电工程中崩塌(滚石)灾害识别与预测方法等开展了相关研究。郭元凯等[2]建立了滚石撞击桥墩三维有限元模型，模拟了桥墩滚石撞击的动力响应。贾兴隆等[3]建立江中输电塔撞击有限元模型，分析了输电塔不同部位的位移响应时程以及撞击力特点。刘成清等[4]对滚石各个运动阶段进行公式化推导，并结合现有滚石模型进行验证。严波等[5]分析了输电塔在覆冰和风荷载作用下的动力稳定性。王丽平[6]分析了不同冲击能量下角钢薄弱点的变形响应以及冲击受损后角钢的承载能力减损情况。Guo等[7]针对杆塔状态评估方法复杂、实用性差的问题,提出一种符合实际需要的杆塔健康状态评估实用方法。Hu等[8]建立了输电塔系统可靠性评估模型并定义了可靠性相关指标。Hisashi等[9]调研统计了日本某铁路发生落石冲击事件中的落石冲击能量，发现落石冲击能量大于10 kJ的落石情况占总落石事件的55%。

上述研究为输电塔滚石撞击分析奠定了坚实的基础。但针对山区输电线路滚石撞击研究相对较少，为了满足中国特高压输电线路工程防护的快速发展，输电塔滚石撞击响应特性及破坏机理还有待进一步研究。为此，以某800 kV特高压直流输电塔线滚石撞击为例，构建山区输电塔滚石撞击有限元模型，分析滚石撞击作用下输电塔动力响应，考察滚石撞击位置、撞击角度、撞击速度以及直径对撞击响应的影响规律，并拟合滚石撞击力峰值计算公式。研究结果可为山区输电塔的防护设计提供理论依据。

1 输电塔滚石撞击模型

T型输电塔总高87.5 m，呼高81 m，塔脚根开20.67 m。塔身结构主要由主材、斜材和辅材连接而成，分沿塔身高度方向，划分13个区段。主件(主材)采用Q420B型角钢，截面有L160 mm×12 mm、L140 mm×12 mm、L140 mm×10 mm、L125 mm×10 mm、L125 mm×8 mm，斜材采用Q345B型角钢，类型包括L90 mm×7 mm、L80 mm×6 mm、L75 mm×6 mm、L70 mm×6 mm，其中L为截面形状样。其他辅材(辅件)使用Q235B型钢材。主材、斜材和辅材参数如表1所示。

1.1 输电塔模型构建

采用Workbench/LS-DYNA非线性动力分析方法，构建滚石撞击输电塔的空间有限元模型，模拟分析滚石撞击塔身。输电塔各角钢构件采用空间Beam梁单元模拟，并运用Hughes-Liu单节积分算法，提高运算效率和准确性。输电塔滚石撞击模型如图1所示。

研究表明，材料的本构关系对仿真计算的影响较大[10]。钢材受撞击时屈服极限明显提高，屈服也会出现滞后现象。因此，考虑钢材应变率的变化，选择塑性随动硬化模型，根据钢材有效塑性应变定义结构失效，钢材屈服强度计算公式为

(1)

表1 输电塔杆件材料参数

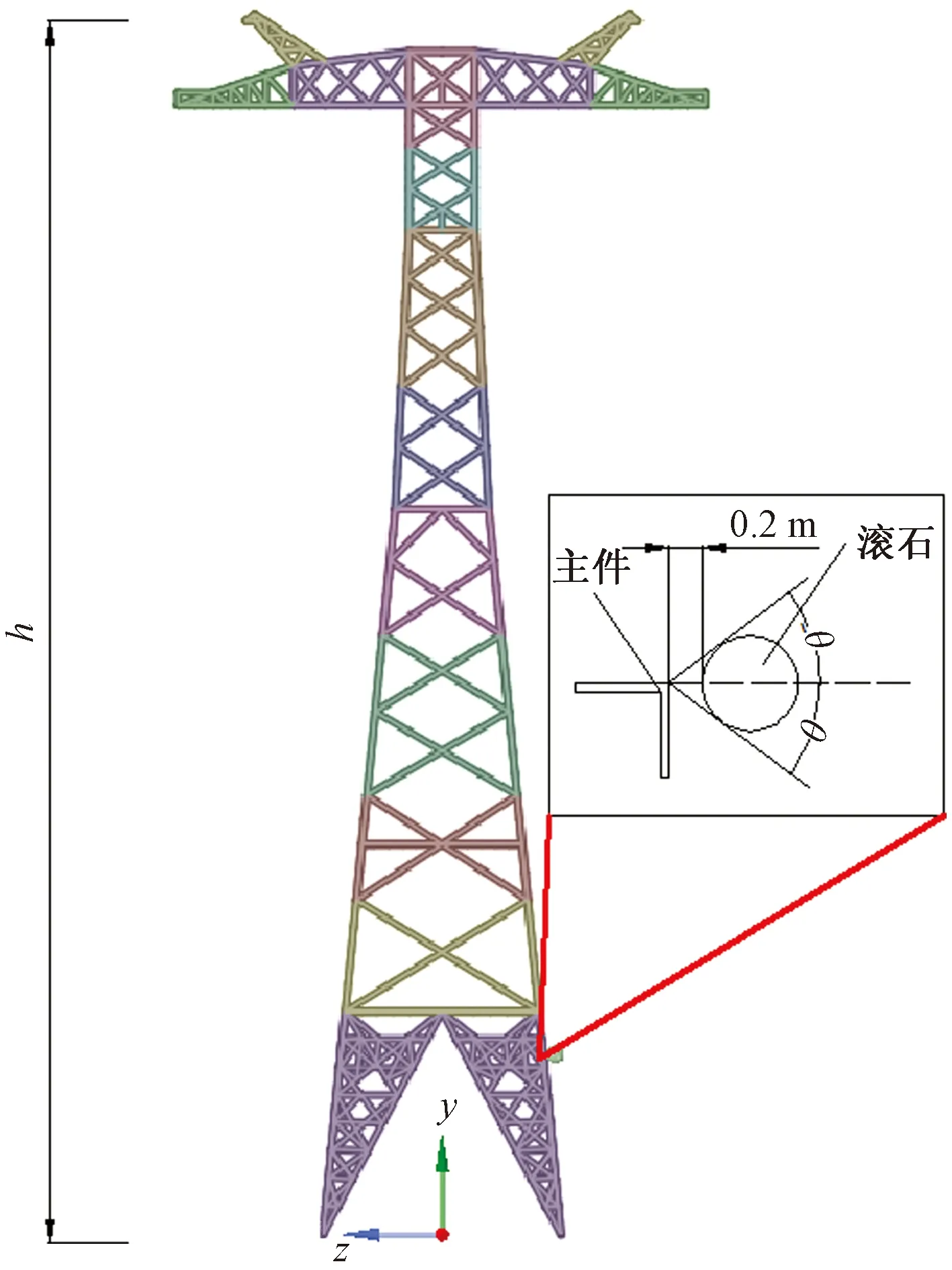
θ为滚石撞击角度；模型x方向为顺线路方向；y方向为塔身竖向; z方向为横担方向，也是滚石撞击的方向；h为塔高图1 输电塔结构有限元模型Fig.1 Finite element model of transmission tower

1.2 滚石撞击参数

为了节省计算机时间，将滚石假定为刚体材料，采用关键字MAT_RIGID进行定义，采用Mass质量单元模拟。滚石与输电塔初始间距为0.2 m，滚石几何模型参照欧洲ETA27标准，选取圆形刚性块。滚石设为花岗岩，密度为2 960 kg/m2，弹性模量5.5 GPa，泊松比为0.21。滚石速度计算公式为[11]

(2)

式(2)中：v0为滚石初始速度；K为滚石质量和形状相关的常数，K=m+J/R2，其中，J为滚石转动惯量，J=0.4mR2，R为滚石半径，m为滚石质量；H为滚石落下高度；βr为滚动摩擦角；α为坡度角；g为重力加速度，g=9.8 N/kg。

1.3 边界条件和接触设置

输电塔塔脚采用固定约束。输电塔塔杆主材、斜材和辅材之间采用高强度螺栓连接，各杆件简化成刚性连接。为了有限元模型节点准确合，采用Design Modeler软件合并Part集命令，使结构共节点形成刚性连接。利用全局网格控制和局部网格控制，进行网格单元划分，达到合理准确的网格化模型。输电塔撞击模型共划分27 223个单元，最小尺寸为0.2 m。

滚石撞击输电塔时，需定义滚石和输电塔接触面，模拟滚石和输电塔之间的接触和滑移。滚石和输电塔撞击接触设为点面接触，采用非对称接触算法计算接触效应。滚石设置为目标面，输电塔的撞击接触区域塔杆为接触面。考虑滚石的不规则性，撞击过程摩擦系数设为0.15，阻尼系数为0.1，衰减常数为0.2。

1.4 撞击模型方法验证

为了验证滚石撞击输电塔建模方法的正确性，依据文献[12]给出的典型滚石撞击输电塔模拟试验参数及研究结果，采用所提出的滚石撞击建模方法，构建缩尺输电塔的有限元模型，分析试验工况下模型撞击力大小，计算撞击角度的加速度峰值，结果表2所示。

由表2可知，有限元仿真结果与实验模拟结果吻合，说明滚石撞击有限元建模方法的正确性。撞击角度为40°时，有限元仿真与实验结果相差较大，分析其原因是撞击边界条件偏差导致。

表2 撞击力模拟结果与实验结果对比

2 输电塔滚石撞击响应分析

参考文献[13-14]，计算典型工况如下：选取滚石速度9 m/s、落石直径1.4 m(质量为4 250.64 kg，体积约为1.436 m3)，撞击角度45°，落石撞击位置为1/6塔高，重点分析输电塔撞击区域塔杆响应。

2.1 滚石撞击力分析

滚石撞击力时程曲线如图2所示。可以看出，撞击接触时间约为0.105 s，滚石撞击力整体上呈现三角脉冲形态，撞击开始撞击力瞬间达到第1主峰值，撞击力最大值达到1 091.2 kN，然后迅速衰减振荡形成第2主峰，撞击力为568.5 kN，最后撞击力衰减为零，撞击过程结束。说明滚石撞击力持续时间短，冲击力大。

图2 撞击力时程曲线Fig.2 Time history curve of impact force

2.2 输电塔杆件轴应力

图3 轴向应力云图Fig.3 Nephogram of axial stress

输电塔撞击区域的塔杆轴应力分布云图如图3所示。由图3可知，在不同撞击时刻，撞击区域塔杆轴向应力最大，远离撞击区域的杆件轴向应力逐渐减小，撞击区域塔杆轴向应力在-214～420 MPa变化。由于斜材横截面较小，在滚石撞击0.4 s时刻，撞击区域斜材轴力应力较大，达到548.3 MPa，接近Q345钢材的极限抗拉强度470～680 MPa，说明此时小截面塔杆受力最为危险。

为掌握滚石撞击输电塔时塔杆主材、斜材和辅材的轴应力时程变化规律，选取碰撞区编号为11990和11997的主件单元，编号23244和23278的斜材单元，编号为15123和15234的辅材单元。各单元编号及位置、轴向应力时程计算结果如图4所示。

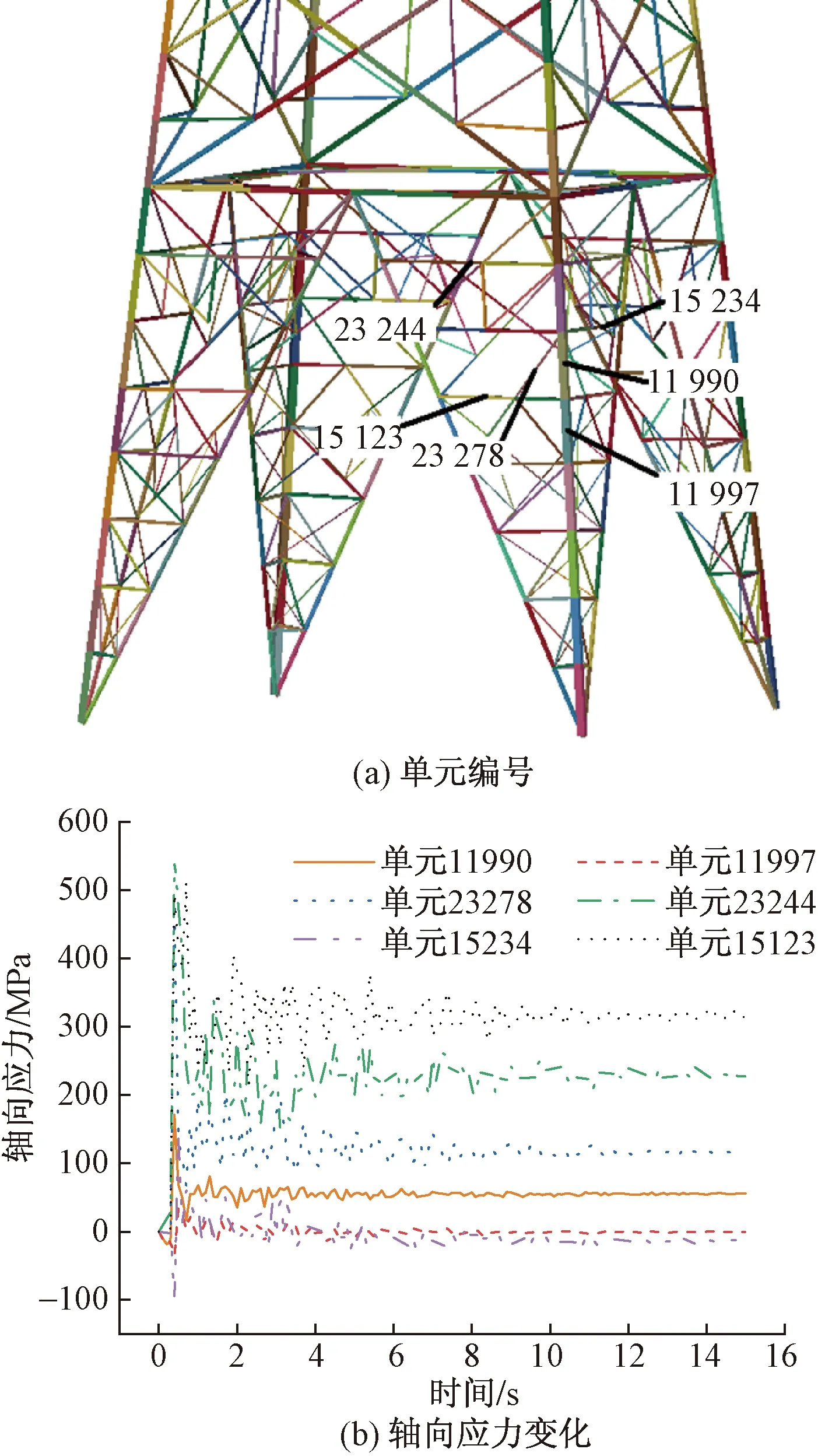
图4 塔杆轴向应力时程曲线Fig.4 Time history curve of axial stress of tower rod

由图4(b)可知，滚石撞击瞬间，输电塔撞击区域的主材、斜材以及辅材的轴向应力急剧增大，较短时间内应力达到峰值，碰撞结束后各杆件轴向应力呈现振荡衰减，并逐渐趋于稳定。编号23244的斜材单元轴向应力出现峰值，达到548.3 MPa，而主材单元轴向应力峰值为171.07 MPa。整体而言，斜材和辅材的轴向应力较大，其原因是斜材和辅材结构尺寸较小，滚石撞击时将承担较大的应力水平。

由图4(b)还可知，滚石撞击后，输电塔撞击区域的塔杆发生了塑性变形，存在残余应力。其原因是输电塔杆件吸收了滚石的动能。由此可见，滚石撞击输电塔时，撞击区域的塔杆轴向应力水平急剧增大，瞬时达到峰值，随后迅速振荡衰减，并趋于稳定。撞击后输电塔塔杆发生塑性变形，存在残余应力。

2.3 输电塔杆件剪应力

撞击区域塔杆剪应力云图如图5所示。选取撞击区域编号为11983和11990主件单元、编号为21724和21916的塔脚主件单元以及编号15125、23260的辅件单元，比较撞击区域塔杆剪应力时程特性，计算结果如图6所示。

由图5可知，撞击区域塔杆剪应力较大，远离撞击区域的杆件剪应力较小。在撞击后0.4 s时刻，塔杆剪应力最大178.6 MPa，但小于材料的极限强度。

图5 剪切应力云图Fig.5 nephogram of shear stress

图6 塔杆剪应力时程图Fig.6 Time history of shear stress of tower rod

由图6可知，滚石撞击输电塔后，塔杆剪应力值呈现先急剧增大后迅速衰减趋势，最后逐渐趋于稳定。撞击过后，塔杆存在残余剪应力。撞击区域的辅件单元23260和15125剪应力峰值最大，分别为150、83.9 MPa；塔脚和碰撞区主材单元的剪应力峰值较小，分别为13.4、4.14、30.4、5.5 MPa。由此可见，滚石撞击时，各塔杆的剪应力变化规律和轴向应力类似，但是撞击区域的塔杆残余剪应力水平小于残余轴向应力。

2.4 塔杆变形分析

输电塔滚石撞击时位移变形如表3所示。

由表3可知，输电塔撞击区域塔杆的位移变形较大，且沿撞击水平Z方向位移大于竖向Y方向位移。撞击区域辅件位移最大，最大水平位移为93.8 mm，最大竖向位移为12.2 mm。

表3 输电塔位移

3 滚石撞击因素分析

为了捕获滚石撞击位置、撞击角度、撞击速度、撞击质量等因素对输电塔受力的影响，分析了不同因素条件下撞击力峰值、主件残余轴向应力的变化规律，并以输电塔撞击区域的主材单元为分析对象。

3.1 撞击位置

滚石直径取1.4 m，撞击速度9 m/s，撞击角度45°，撞击位置从输电塔底部塔脚起算，分别为h/14、h/12、h/10、h/8、h/6、h/4、h/2，其中h为塔高。滚石撞击时塔杆主材撞承受的撞击力、撞击区域的主材残余轴向应力计算结果如图7所示。

由图7(a)可知，随着滚石撞击位置的增高，滚石撞击力呈现先增大后减少趋势。当滚石撞击位置为h/2时，撞击力为706.1 kN；滚石撞击位置为h/6时，撞击力达到1 221.6 kN，其原因是撞击位置越高，滚石传递给输电塔的动能越大。

图7 不同撞击位置时撞击力及主材残余轴向应力Fig.7 Impact force and residual axial stress of the main material at different impact positions

由图7(b)可知，随着滚石撞击位置的增高，输电塔撞击处主件的轴向残余应力也呈现先增大后减少趋势；当滚石撞击位置为h/6时，主件的轴向残余应力达到最大值238.4 MPa。由此可见，滚石撞击位置在h/6～h/8范围，滚石撞击力峰值和杆件的残余轴向应力较大。建议在输电塔该位置处，安装相应的防护设备，保证输电塔的运营安全。

3.2 撞击角度

滚石直径1.4 m，撞击速度9 m/s，撞击位置为h/6，撞击角度θ为-45、-35°、-25°、-15°、-5°、0°、5°、15°、25°、35°、45°。撞击区域的塔杆主材撞击响应计算结果如图8所示。

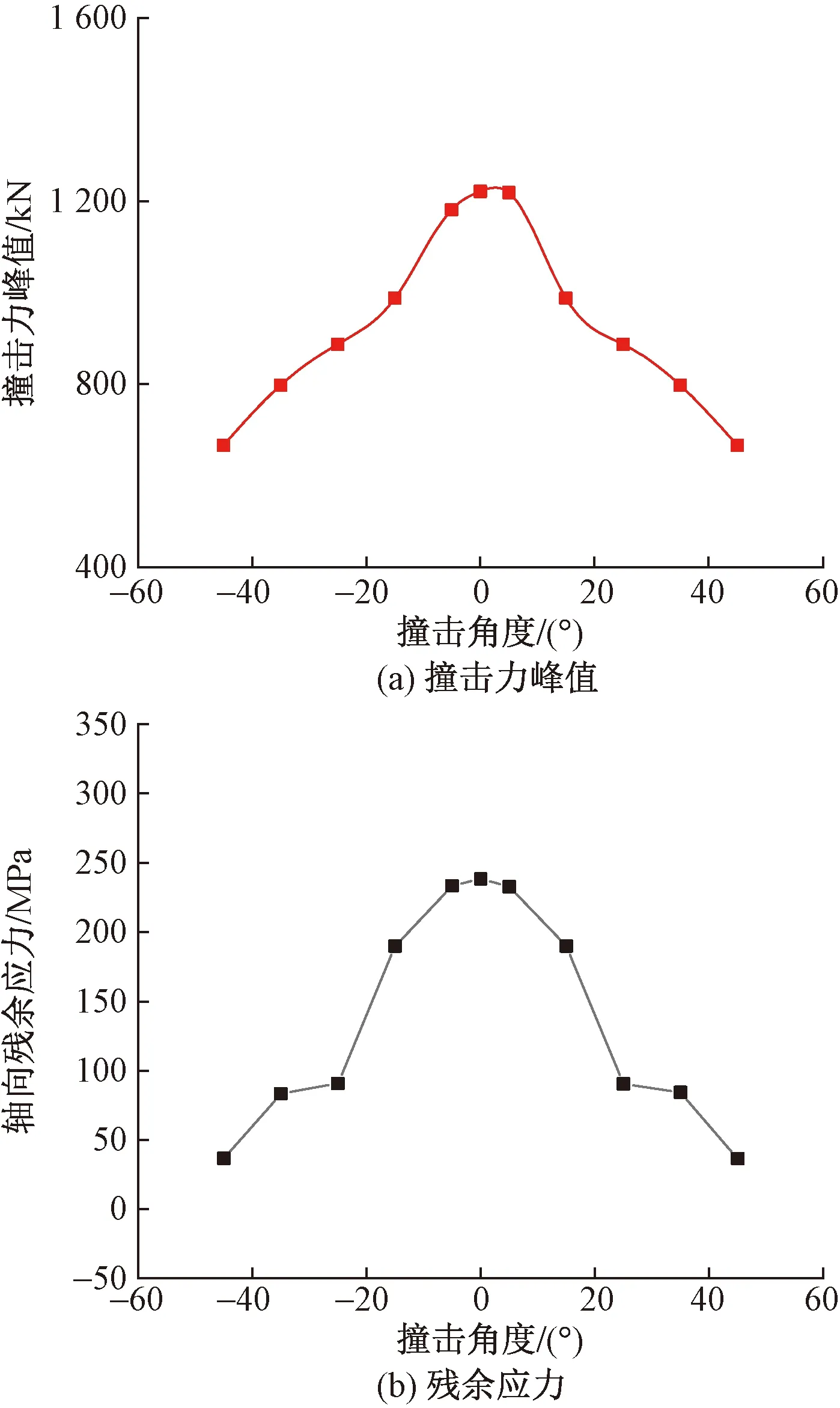
图8 不同撞击角度时撞击力及主材残余轴向应力Fig.8 Impact force and residual axial stress of the main material at different impact angles

由图8(a)可知，随着滚石撞击角度的增大，滚石撞击力呈现先增大后减少趋势；当滚石撞击角度为0°时，撞击力达到最大值为1221.7 kN。由此可见，滚石与输电塔的撞击角度为0°时，撞击力响应最为剧烈。

由图8(b)可知，随着滚石与输电塔的撞击角度增大，输电塔撞击处主材的轴向应力呈现先增大后减少趋势；在滚石撞击角度为0°时，主件的轴向应力达到最大值238.4 MPa；-45°和45°时，输电塔主件的轴向应力相对较小。由此可见，滚石的撞击角度对输电塔的影响较大，撞击角度为0°时，输电塔的撞击响应最为剧烈。

3.3 撞击速度

滚石直径1.4 m，撞击位置为h/6，撞击角度为45°，滚石撞击速度分别为1、3、5、7、9、11、13、15、17、19、21、23、25、27、29 m/s。输电塔的撞击响应如图9所示。

由图9(a)可知，随着滚石撞击速度增大，滚石撞击力呈非线性增大趋势；当滚石撞击速度为1 m/s时，撞击力为162.28 kN；滚石撞击速度增大为31 m/s时，撞击力达到最大值为2 356.603 kN。

由图9(b)可知，随着滚石运动速度不断增大，输电塔主件的轴向应力呈现增大趋势；轴向应力增长呈现两个阶段，即先快速后缓慢：滚石运动速度在1～13 m/s时，主件的轴向应力增长快，撞击速度位于13～31 m/s，主件的轴向应力增长慢。由此可见，滚石的撞击速度越大，输电塔的撞击力响应越大。

3.4 撞击直径

撞击高度h/6，撞击速度9 m/s，撞击角度为45°，滚石直径为0.2、0.4、0.6、0.8、1.0、1.2、1.4、1.6、1.8、2.0、2.2、2.4、2.6、2.8 m。撞击区域的塔杆主材撞击响应计算结果如图10所示。

图9 不同撞击速度时撞击力及主材残余轴向应力Fig.9 Impact force and residual axial stress of the main material at different impact speeds

图10 不同撞击质量时撞击力及主材残余轴向应力Fig.10 Impact force and residual axial stress of the main material at different impact masses

由图10(a)可知，随着滚石撞击直径增大，滚石撞击力呈现非线性增大趋势。当滚石撞击直径为0.6 m时，撞击力峰值为236 kN；滚石撞击速直径为1.8 m时，撞击力峰值达到最大值为1 450 kN。

由图10(b)可知，随着滚石直径不断增大，输电塔主件的残余轴向应力呈现增大趋势，且与撞击力增长趋势类似；在滚石撞击直径为0.6 m时，主件的轴向应力为59.1 MPa，滚石撞击直径为1.8 m时，主件的轴向应力为136 MPa。由此可知，滚石的直径越大，输电塔撞击响应越大。

综合因素分析可知，撞击速度和滚石直径对输电塔撞击损伤影响较大。撞击角度和撞击位置相对较小。目前输电线路设计规范，并未明确给出滚石撞击输电塔的具体防治意见，建议在设计时重点关注高边坡滚石灾害地区，并增大滚石撞击侧输电塔主件材料的受力面积(宽度和厚度)和强度，防撞设备的布置主要针对来自0°方向和h/6～h/8处的撞击区域。

4 滚石撞击力峰值计算公式

为了估算滚石撞击力，选用滚石直径和滚石速度作为主要拟合因素，拟合滚石撞击力峰值计算公式。不同直径D、撞击速度条件下滚石撞击力峰值如表4所示。

撞击力峰值拟合分两个步骤，首先对同直径的滚石不同撞击速度与撞击力峰值进行拟合，得到不同直径拟合的系数C′、E，其次对同速度的滚石不同直径指数系数E取平均值，并简化成一个固定指数，最后对不同直径的速度与撞击力峰值进行再次拟合，得到相关指数E拟合的新的系数C′，拟合结果如表5所示。

根据上述思路可进行数值拟合，得到撞击力峰值与滚石速度拟合关系式为

PM=C′V0.82

(3)

拟合系数E是一个与质量无关的固定系数，对于滚石撞击力峰值与速度的函数关系表达式必包含与直径有关参数，所以拟合的系数C′应该与直径相关。再次拟合的系数C′与滚石直径，如图11所示。

表4 各参数作用下撞击力峰值

表5 撞击力峰值与速度拟合

由图11可知，相关系数C′与滚石直径呈现正相关，且相关系数R趋近于0.95。相关系数C与直径D的拟合关系为

C′=89.63lnD+131.78

(4)

将式(4)代入式(3)，可得到输电塔撞击力峰值与滚石直径和速度的关系表达为

PM=(89.63lnD+131.78)V0.82

(5)

式中：PM为滚石撞击力峰值，kN；V为滚石的撞击速度，m/s；D为滚石的直径，m。

为了验证滚石撞击输电塔撞击力峰值的简化计算公式正确性，选取两组因素与有限元计算值进行比较，第1组撞击角度为0°，位置h/6，直径为1.4 m，滚石速度依次为1、13、17、19 m/s；第2组撞击角度为0°，位置为h/6，速度为9 m/s，直径分别为1、1.8、2.2、2.6 m，结果如表6所示。

由表6可知，撞击力峰值拟合公式计算结果与有限元计算结果基本吻合。说明了撞击力峰值计算公式的合理性。但少数工况下撞击力峰值的误差偏大，其原因是拟合计算公式只考虑的滚石直径和滚石速度，若要提高计算精度，还需要考虑更多的影响因素。

选用瑞士算法[式(6)]和隧道手册[式(7)]进行比较[15]，其中，瑞士算法是瑞士学者 Labiouse结合Hertz理论及室内试验，给出的一种冲击力半理

图11 相关系数C′与滚石直直径关系曲线Fig.11 Relation curve between correlationcoefficient C′ and straight diameter of rolling stone

表6 公式计算值与有限元值的比较

论半经验算法[式(6)]；隧道手册是《公路隧道设计手册》[16]中结合动量定理，给出的一种滚石冲击力的计算方法[式(7)]。分析撞击力峰值公式的适用性。滚石撞击角度为0°，撞击位置为h/6，直径为1.4 m，速度为1～21 m/s，计算结果如图12所示。

(6)

式(6)中：P为滚石冲击力；R为滚石半径；ME为垫层土体的弹性模量；Q为滚石的重量；H为滚石的下落高度。

(7)

式(7)中：v0为滚石速度；h为滚石下落高度；ρ0为垫层土体的密度；c为压缩波波速；μ为垫层材料的泊松比；tw为滚石下落时间。

由图12可知，现有规范公式与所拟合撞击力峰值公式都是随着速度的增加呈现非线性增大的趋势；瑞士算法[式(6)]计算的峰值最大，其次是隧道手册[式(7)]，拟合的计算公式计算结果最小。

图12 滚石撞击速度与撞击力关系曲线Fig.12 Relation curve between impact velocity and impact force of rolling stone

5 结论

以800 kV特高压直流电输电塔为研究对象，构建了山区输电塔滚石撞击有限元模型，分析了滚石撞击作用下输电塔动力响应，考察了滚石质量、撞击速度、撞击角度和撞击位置对输电塔内力的影响规律，并给出了滚石撞击力峰值计算公式，得出如下结论。

(1)输电塔遭受滚石撞击时，将承受持续时间较短，冲击力大的脉冲荷载。滚石撞击区域的塔杆位移较大，塔杆撞击方向的水平向位移大于竖向位移，辅件整体变形较大。

(2)输电塔撞击区域的塔杆轴向应力和剪应力较大，远离撞击区域的杆件轴向应力逐渐减小，且小截面塔杆受力最危险。

(3)滚石撞击时，输电塔各杆件轴向应力瞬时达到峰值，随后迅速振荡衰减，并逐渐趋于稳定，且各杆件均出现残余应力。各塔杆残余剪应力变化规律和轴向应力类似，但是残余剪应力水平小于输电塔的轴向应力。

(4)撞击角度为0°时，输电塔的撞击响应最为剧烈。相比于其他撞击位置，滚石撞击h/6～h/8塔高处，滚石撞击力峰值和杆件的残余轴向应力相对较大。

(5)滚石直径和撞击速度对输电塔撞击响应影响较大，滚石直径和撞击速度越大，输电塔的撞击力响应越剧烈。该拟合公式可用于输电塔滚石撞击力峰值估算。