考虑道路受损的震后应急物资运输路径优化
闫森, 齐金平,2*, 张儒
(1.兰州交通大学机电技术研究所, 兰州 730070; 2.甘肃省物流及运输装备信息化工程技术研究中心, 兰州 730070)
中国地震灾害频发,给人们的生命财产造成了巨大的损失,应急物资的配送在救灾过程中十分重要。合理的规划配送路径,不仅能够保证物资送达的及时性,还能降低成本,能有效地提高物流效率。中外学者在这方面已开展了大量的研究。Bozorgi等[1]考虑需求、时间和运输成本的不确定,引入需求不满足率为优化目标,并同时考虑时间和成本最小,建立了配送路径优化模型;Shiri等[2]考虑需求时间的不确定性,利用陆运和空运两种运输方式,建立了不确定条件下的混合整数非线性开放位置路径优化模型;Maharjan等[3]考虑总成本和需求覆盖率两个目标,建立了临时物流枢纽可靠性分配模型;Maghfiroh等[4]面对不可预测的需求和条件,提出了考虑随机和动态情况的路径优化模型;Jeong等[5]考虑时间重要性,需求信息的不确定性和动态性以及信息传递的不确定性建立模型;刘松等[6]考虑运输环境和速度的不确定性,建立了带班期限制的鲁棒路径优化模型;梁永梅等[7]分别以路径最短和时效性最优为目标求解了应急医疗物资配送模型;曲冲冲等[8]以时效性与分配公平性为目标,建立了多种运输方式、多时段的配送路径优化模型。上述文献针对运输时间、物资需求的不确定性,以及路径优化的多种目标进行了研究,但其对需求不确定性的界定,物资种类的多样性和路网的破环性研究有所欠缺。Rawls[9]和Salman等[10]考虑道路受损,建立了成本最小化的路径优化模型;Petroianu等[11]考虑车辆数量、道路通行性和天气条件等因素,建立了应急物流路径优化模型;狄卫民等[12]地震灾害对道路的损毁,道路复杂程度和需求等不确定性因素,提出了物资拆分配送的方法,建立了应急物资配送模型;张乃平等[13]考虑震后道路损毁和需求不足等因素,以分配公平性最大和配送总时间最小为目标构建了分配-运输模型。上述研究考虑到了地震灾害中道路的受损情况,但其对道路受损率的界定和对运输的影响研究不够深入,未考虑到道路通行能力和需求点时间窗约束的影响,这会对实际的救灾效率产生影响。
Kara等[14]用各种的算法求解了带时间窗的TSP问题;韩孟宜等[15]以运输成本和惩罚成本之和最小为目标,构建了带时间窗约束的路径优化模型;陈畴镛等[16]考虑道路时间窗及配送次序公平性因素,构建了运输时间最短和惩罚成本最少的双目标模型;姚书婷等[17]建立了多禁止时间窗的应急物资配送路径优化模型;郭咏梅等[18]以物流响应能力最大化为目标建立了等带时间窗的车辆路径模型;李卓等[19]以系统满意度最大、系统配送时间和总成本最小为优化目标,建立带软时间窗的多目标混合车辆路径优化模型。以上研究加入了救灾点时间窗的约束,但都是基于单一配送中心的路径优化,实际的应急物流是错综复杂的,可能包含多配送中心,多种应急物资和不确定信息等情况。在路径优化模型求解方面,由于选址-路径问题(Location-Routing problem, LRP)的(non-deterministic polynomial hard,NP-hard性质,遗传算法,蚁群算法,多头绒泡菌算法,智能水滴算法和强化学习算法等启发式算法具有良好的求解效果[20-21],但对算法的求解精度和收敛性还可以进一步的研究。
地震灾害由于其强大的破环性会对道路造成损坏。为此,从运输速度和道路通行能力等方面考虑地震灾害对道路的损毁情况,利用多种因素确定道路损毁率,针对多应急物资种类、多配送中心的物流网络,以配送时间和配送成本最小为目标,建立了考虑道路受损的带时间窗约束的应急物资运输路径优化模型,并设计遗传算法和模拟退火算法的混合算法求解该模型,为应急救援物资配送提供科学决策,减少地震灾害带来的人员和财产损失。
1 问题描述
地震发生后,在应急物流网络中产生V个节点,包括P个配送中心与M个需求点,救灾车辆需要在时间窗内将救灾物资送往需求点。由于应急物流的突发性和不可预知性,需求点对物资的需求量由三角模糊数表示。每个需求点规定两个时间窗,一个为惩罚时间窗,另一个为硬性时间窗。即当车辆在惩罚时间窗与硬性时间窗之间到达时,会造成人员或财产的损失,产生惩罚成本。所有车辆必须在硬性时间窗内到达。而每条道路由于其地形、与震中的距离、道路等级等因素的不同也会有不同的受损情况。问题的目标是在考虑道路受损的情况下,尽量在各需求点的时间窗内,选择合适的配送中心和配送路径对需求点进行配送,使得总的配送时间和配送成本最小。
根据问题的特点,提出如下假设:①应急车辆在不考虑道路受损时的配送速度为正常速度;②应急车辆在需求点的停留时间可以忽略不计,假设停留时间为0。
2 模型建立
2.1 道路通行能力和行驶速度计算
(1)通行能力计算。地震发生后,道路会由于其自身的损坏程度和周边设施的损坏程度影响通行能力。为了方便研究,道路的损坏程度由道路的损毁率表示,其计算方法为式(2),周边设施的损坏程度由需求点的受灾程度表示,根据文献[22]得到道路受损后的通行能力计算公式为
C=C′(1-α)(1-β)
(1)
α=
(2)
式中:C为考虑道路受损时的通行能力;C′为道路正常情况下的通行能力,可通过查询公路通行能力手册得到;α为道路的损毁率;Dj为需求点j到震中的距离;yj为需求点j的地形;Mou为山地地形;Pla为平原地形;TR为二级公路;TFR为三级公路和四级公路;Rl为路径l的道路等级;β为受灾程度,根据地震发生后收集的受灾信息确定。
(2)行驶速度计算。震后车辆在有受损情况的道路上的行驶速度与道路损毁率有关,根据文献[23]建立的模型并进行改进,得到考虑道路受损时的行驶速度的计算公式为
(3)
式(3)中:v为救灾车辆考虑道路受损时的平均行驶速度;v′为救灾车辆正常情况下的平均行驶速度。
2.2 模型构建
模型的目标为应急救援的总时间和总成本最小,总时间为车辆运输时间;应急救援成本包括车辆固定成本,各节点之间的运输成本以及违反时间窗的惩罚成本。模型可表示为
(4)
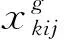
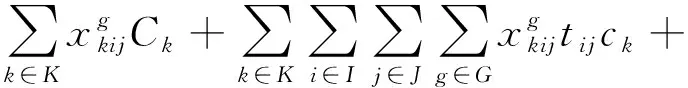
(5)
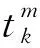
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
模型中,式(4)、式(5)为目标函数,式(4)为运输时间最小;式(5)为救援成本最小,主要由车辆的固定成本、运输成本和超出时间窗的惩罚成本组成;式(6)表示需求量的满足;式(7)为库存约束,表示配送中心的应急物资运输量总和不超过其最大库存;式(8)表示每个需求只对应一个配送中心;式(9)表示道路通行能力的约束;式(10)表示硬性时间窗约束;式(11)表示车辆容量约束;式(12)表示车辆开始运输时的时间记为0;式(13)~式(16)表示决策变量的约束。
3 模型求解
3.1 不确定约束条件的处理
(17)
3.2 双目标的处理
在模型中,时间目标和成本目标是由于时间与成本的计量单位不同,对目标进行简单的线性加权法也不合理。为此我们考虑通过计算单目标的最优值来将两个目标单位消除。因此目标函数f1和f2可表示为
(18)
3.3 算法设计
采用遗传算法-模拟退火算法(genetic algorithm-simulated annealing,GA-SA)混合算法进行求解,在遗传算法的变异操作和适应度函数中加入模拟退火算子,可以解决遗传算法种群早熟问题,确保结果向全局最优解收敛。
Step 1编码方法。Mpoint个需求点,Pcenter个配送中心,采用双层编码,第一层编码长度为Mpoint,基因为1-Mpoint,表示节点的访问顺序。第二层编码为长度为Mpoint的整数编码,基因位为[1,Pcenter]的整数,表示节点由什么配送中心服务,其中Pcenter为配送中心数量。
Step 2遗传算子设计。
(1)变异。采用两点互易进行变异:①产生2个随机自然数r1、r2;②交换第r1位和r2位的基因。
(2)两点交叉。①随机选择两个染色体作为父本;②产生2个随机自然数r1和r2;③将两个父本染色体r1~r2的基因片段进行交换, 得到两个子代染色体,并对得到的两个染色体进行修订处理,使得不发生冲突
(3)修补方法。交叉后, 取交叉片段的补集重新随机排列到非交叉片段。
Step 3选择设计。采用轮盘赌选择。
Step 4模拟退火算子。
在遗传算法中加入模拟退火算子,模拟退火的基本原理如下:①某个温度T下得到一个解(这个解用遗传算法优化得到);②如果这个解比上一个温度的解好,则接受这个新的解,否则转③;③计算T下的概率,其计算公式为
(19)
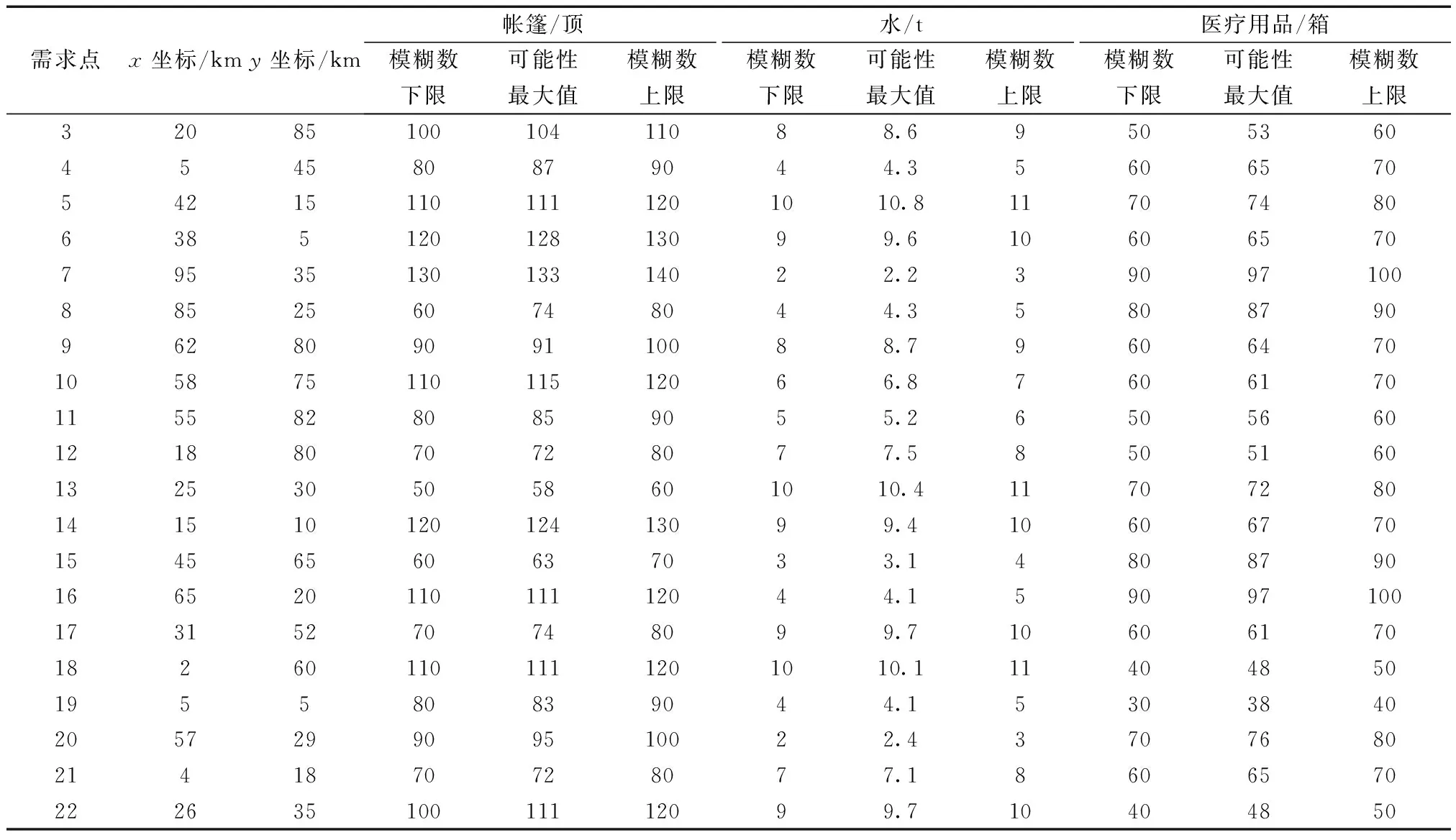
式(19)中:dE为目标函数变化量;k为冷却系数;随机产生[0,1]区间的随机数a,如果a 已知点A(75,70)为震中,该应急物流网络内有2个配送中心,20个需求点以及3种应急物资。应急物资为帐篷、水和医疗用品,体积分别为0.2 m3/顶、1.5 m3/箱、0.2 m3/t,车辆容量为40 m3/车,正常情况下的行驶速度为60 km/h,固定成本为每辆300元,配送过程中单位运输成本为5元/km,违背时间窗单位惩罚成本为4元/min。配送中心以及需求点相关信息分别如表1、表2所示。 表1 配送中心信息Table 1 Distribution center information 设种群规模N=200,最大迭代次数Maxgen=200,交叉概率=0.8,变异概率=0.1, 冷却系数=0.95,初始温度T0=2 000,终止温度Tend=20,T=T0。使用MATLAB软件,分别用一般遗传算法与上述设计的算法进行求解,目标值的收敛变化情况如图1所示。各节点之间的路径如图2所示。具体路径信息如表3所示。 可以看出,SA-GA比遗传算法所得结果的配送总时间降低5.4%,总成本降低了4.4%,表明了SA-GA比遗传算法有更好的求解效果。 图1 算法迭代比较Fig.1 Algorithm iteration comparison 表2 需求点信息Table 2 Demand point information 图2 优化路径结果Fig.2 Optimizing path results 表3 路径信息Table 3 Path information 表4 考虑与不考虑道路受损的结果对比Table 4 Comparison of results considering and not considering road damage 为了进一步验证构建模型的有效性,求解不考虑道路受损的应急物资物流车辆路径,其结果如表4所示。 通过对比发现考虑道路受损的最优配送路径可以更多的在惩罚时间窗内送达,同时可使总时间减少7.5%,总费用减少5.0%。而在时间性要求非常高的应急物资配送中,更多的物资在时间窗内运达,会对灾害造成的损失有一定的抑制作用。因此,所建立的路径优化模型对地震灾害发生时的道路受损进行了较好地还原,更加符合实际场景,同时还对成本和时间进行优化,表明了本文模型的有效性。 (1)考虑了地震灾害对道路的损坏,考虑多种应急物资种类,并在其需求量不确定的情况下的进行应急物资配送路径优化,以配送时间最小和总成本最小为目标建立了带时间窗的双目标模型。 (2)考虑了在配送过程中物资的需求量具有不确定性,使用三角模糊数对应急物资需求量进行描述;考虑地震灾害中道路损毁,结合需求点到震中的距离、地形、公路等级等因素来确定道路损毁率,利用道路损毁率来描述其对车辆行驶的影响,更加符合实际情况,并且提高了路径优化的准确性。 (3)设计了GA-SA算法对模型进行求解,在遗传算法的变异操作中加入了模拟退火算子,解决遗传算法种群早熟问题。算例表明,该算法对收敛速度和求解结果都有提升,可以解决考虑道路受损的应急物资配送路径优化问题。进一步对比考虑与不考虑道路受损的结果,考虑道路受损在运输总时间和总费用都有减少,产生惩罚成本的时间减少了41 min,验证了算法与模型的正确性和适用性。 地震灾害中道路其受损情况会由于余震和道路修复产生动态变化。因此,应进一步考虑道路受损动态变化的情况,使应急物资配送路径优化更加考虑实际,更具科学性。4 算例分析
4.1 算例描述
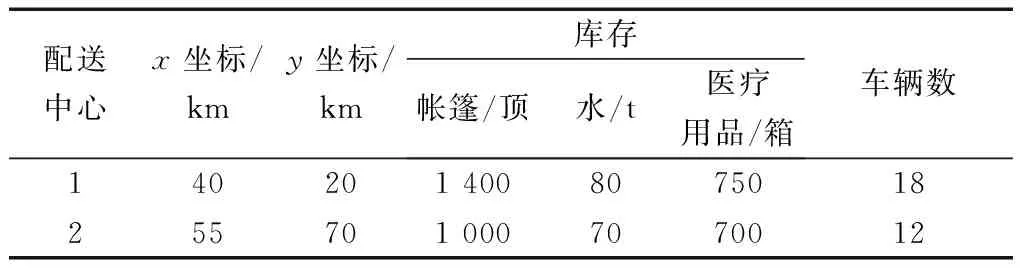
4.2 算法结果
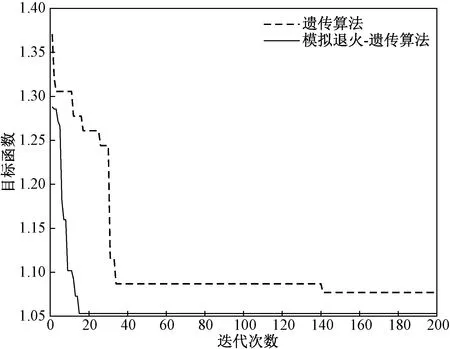
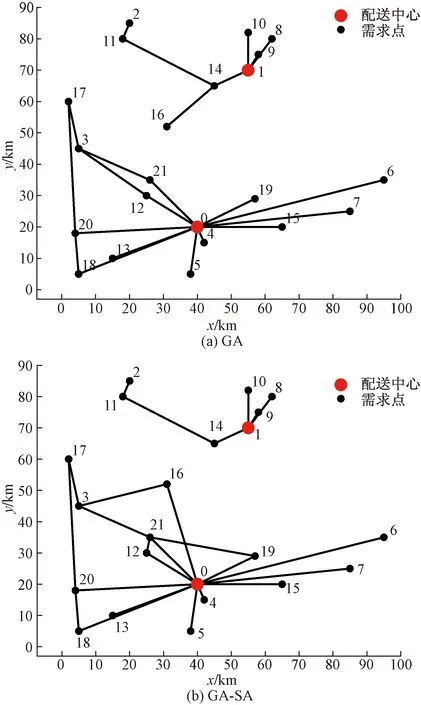


5 结论

