斜弯独塔混合梁斜拉桥参数敏感性分析

杨懋， 缪长青， 王旭东

(东南大学土木工程学院， 南京 211189)

斜弯独塔混合梁斜拉桥作为一种新型的斜拉桥结构形式，结合了钢箱梁跨度大和混凝土箱梁刚度大的优点，具有良好的受力性能、跨越能力和经济性，斜弯桥塔也增加了桥的美观性。同时，复杂的体形结构也增加了施工难度，受结构参数变化影响程度大。

近年来，学者们针对各类斜拉桥的参数敏感性分析开展了大量研究。王生武等[1]以安徽某大桥为背景，详细分析了成桥状态下，桥梁结构自重、斜拉索索力和整体温度三种参数对异型独塔斜拉桥的影响。鲍英基等[2]以洪溪特大桥为研究对象，研究拉索索力、预应力、桥面铺装层厚度以及混凝土徐变系数4个参数对预应力混凝土梁矮塔斜拉桥运营阶段主梁的应力和位移的敏感性。周勇军等[3]以某预应力混凝土矮塔斜拉桥为工程背景，选取梁重度与刚度、斜拉索初张力与刚度、温差荷载和预应力效应为控制对象，研究了其对成桥状态下主梁线形的影响程度，并根据敏感程度大小将各参数划分成3个等级。

目前，斜拉桥参数敏感性的研究对象主要集中在主梁形式单一的预应力混凝土梁斜拉桥或者钢箱梁斜拉桥，对参数的选择多为主梁自重、预应力和整桥整体温度变化，对于异型桥塔混合梁结构体系的参数敏感性研究较少，且缺少较为明确的敏感度评估体系。鉴于此类桥梁在运营和成桥过程中受到的影响因素较多，为研究此类斜拉桥的参数变异对成桥结构状态的影响规律，以一座异型桥塔混合梁斜拉桥为背景，引入无量纲的参数敏感度指标，以该桥成桥状态下的结构响应(内力、位移、索力等)为控制目标，分析成桥状态下不同结构参数影响结构状态的敏感度。

①～④轴线分别为0号墩、桥塔墩、辅助墩和边墩图1 纬二桥桥型布置图Fig.1 Bridge layout of Wei’er Bridge

1 工程概况

本桥为异型斜弯独塔斜拉桥，采用墩、塔、梁固结结构体系，桥梁主梁部分为钢-砼混合梁结构形式，桥梁跨径布置为47 m+86 m+29 m=162 m，如图1所示。桥边跨采用61 m预应力混凝土箱梁，材料采用C60混凝土，且箱梁高度沿桥纵向变化；主跨为101 m扁平钢箱梁，材料选型Q345qD钢材，钢箱梁钢板厚度随钢箱梁段位置而改变；混凝土梁和钢梁之间通过2.5 m钢-混结合段连接，标准段桥梁中心线处高1.9 m，箱梁宽度为51 m，桥塔为变截面斜弯钢塔，塔高约42 m，倾斜角度随高度变化，沿横桥向对称布置。钢桥塔分为上下两个塔柱，上塔柱高29 m，为单肢矩形截面，下塔柱高13 m，为双肢矩形截面。主跨布置24根斜拉索，为放射状双排索，上端锚固于主塔上，下端锚固于钢箱梁上；边跨布置4根背索，上端锚固于主塔上，下端锚固于混凝土主梁中间及端横梁附近。

2 有限元模型建立

采用MIDAS Civil有限元软件进行空间结构分析，以左侧支座点为原点，建立全桥空间杆系模型，如图2所示。主梁采用鱼骨梁模型，梁截面采用截面特性值计算法导入，其中预应力混凝土箱梁单元采用Plane形式生成截面，计算截面特性，通过变截面组平滑连接各混凝土箱梁；钢箱梁单元采用Line形式生成截面，计算截面特性计算，钢箱梁厚度随桥纵向变化；钢混结合段通过实心混凝土箱梁和钢箱梁叠加组合模拟[4]。对斜拉索，考虑拉索的垂度效应，采用只受拉桁架单元模拟，并通过Ernst公式对其弹性模量进行折减。异型桥塔同样选取梁单元模拟，导入带肋空心钢梁截面，通过调整梁单元的倾角及创建变截面组顺滑连接各单元[5]。分别通过约束全自由度的支座和可纵向活动的竖向铰支座模拟桥塔、梁、桥墩固结作用和辅助边墩支撑作用；在塔梁连接处建立简化的无容重混凝土横梁，模拟塔梁墩固结处内力及刚度的分配关系；斜拉索与主梁和桥塔通过刚臂进行连接。

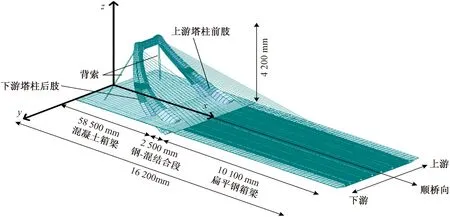
图2 桥梁整体MIDAS模型Fig.2 The overall MIDAS model of the bridge

3 结构参数敏感性分析

鉴于异型桥塔混合梁斜拉桥是一种由混合梁、异型塔、斜拉索三种构件组合成的复杂空间超静定体系，与传统桥梁结构的受力特点存在较大的区别，文中选用结合段位置、桥塔局部温度、斜拉索初张拉力和背索倾斜角度四个参数进行敏感性分析。在其他参数不变的情况下，控制单一参数变化，以成桥状态下结构响应(桥塔和主梁的内力、位移以及索力等)为控制目标，定性分析参数变化对结构响应参数的影响，确定关键参数对结构响应的敏感性[6-7]。同时为了定量评判各个参数对控制目标的影响程度，通过选取结构特性值变化量与关键结构参数变化量的比值作为敏感度评判标准[8]。敏感度公式为

(1)

式(1)中：sensi是一组无量纲的非负实数，反映成桥状态下控制目标p对参数变量i的敏感程度；Δp、Δi分别为控制目标和参数变量的变化量。

通过对sensi中各实数的大小比较，可以对成桥状态下各关键结构参数的敏感性进行评估。

在固定其余参数不变的情况下，以塔梁固结处弯矩值、桥顶纵向位移值、背索S1索力值、主梁跨中挠度作为控制目标，计算某一参数变量在可能范围内的摄动值下控制目标值并组成控制点，采用牛顿差值公式[式(2)]，拟合出控制点的关系式，得到控制目标随着参数变化的变化曲线函数N(x)。对于结构参数变量x，敏感度可用式(3)对变化曲线函数求一阶导数近似计算[9-10]。

二次牛顿差值公式为

N(x)=f(x0)+(x-x0)f[x0,x1]+

(x-x0)(x-x1)f[x0,x1,x2]

(2)

式(2)中：x为某单一结构参数变量；x0、x1、x2为3种工况下控制目标值。

(3)

3.1 钢混结合段位置的影响分析

在斜弯独塔混合梁斜拉桥中，钢梁与混凝土梁结合段的位置直接改变了混合梁斜拉桥的质量和刚度分布，是主梁刚度的突变点，对斜拉桥的受力和变形有着很大的影响，因此有必要通过改变钢混结合段位置，研究其对结构的影响程度并确定敏感度大小[11-12]。选取结合段顺桥向距离实际设计位置4.5、6.5、8.5 m三种情况。

为了便于进行钢混结合段位置对于控制目标的影响分析，采用混凝土梁和钢梁的跨度比η的概念[式(4)]，其中混凝土梁跨度为混凝土箱梁跨度和钢混结合段跨度总和，具体数值如表1所示。

(4)

图3、图4给出钢混结合段在3个不同位置时，下游塔柱钢混结合段位置变化前后的弯矩和正应力的差值。可以看出，结合段位置离实际位置距离增大时，下游塔柱弯矩和正应力均减小，且随着钢混结合段越远离桥塔，桥塔弯矩和正应力变化幅值越明显，跨度比达到0.751时，桥塔弯矩最大变化幅值达到1 400 kN·m，正应力最大变化幅值也达到0.9 MPa。

图5、图6给出钢混结合段在3个不同位置时主梁挠度值和钢混结合段位置变化前后的差值。由图可见，钢混结合段的位置变化对主梁和桥塔线形都产生了较大的影响。主梁中跨发生下挠，最大变化幅度值达到25 mm，主梁边跨产生上挠，沿桥纵向方向挠度变化值基本成对称分布，且随着钢混结合段越远离桥塔，竖向挠度变化幅值都呈增大规律。在混凝土梁和钢梁的跨度比为0.699的工况下，桥塔纵向变形未出现较大变化；在混凝土梁和钢梁的跨度比为0.714和0.751的工况下，桥塔纵向变形出现较大浮动，变化幅值明显增大，最大差值达到4.5 mm。

表1 混凝土梁和钢梁的跨度比Table 1 Span ratio of concrete beam and steel beam

表2列出了钢混结合段位置变化前后所选4个控制目标的数值，并根据式(2)、式(3)计算出敏感度。由表2结果可知，钢混结合段位置对斜弯独塔混合梁斜拉桥梁结构响应的影响程度从大到小依次为：塔顶纵向位移、主梁最大挠度、背索索力和塔梁固结处弯矩。其中，混凝土梁和钢梁的跨度比增大15.73%时，塔顶纵向位移、主梁最大挠度将分别减小30.3%，增加29.4%。混凝土梁和对钢梁的跨度比变化18.2%时，塔顶纵向位移、主梁最大挠度、将分别增加162.8%%，增加37.5%。混凝土梁和钢梁的跨度比变化24.4%时，塔顶纵向位移、主梁跨中挠度、将分别增加211.8%，增加41.8%。而混凝土梁和钢梁的跨度比增大时，背索索力、塔梁固结处弯矩较初始位置变化很小。由以上分析可以看出，塔顶位移和主梁挠度对钢混结合段位置较为敏感，而其对背索索力和塔梁固结处弯矩影响较小。表明斜弯独塔混合梁斜拉桥桥塔和主梁的线形容易受到结合段位置的影响，对控制桥梁变形起到了重要作用，在设计阶段应重点考虑。

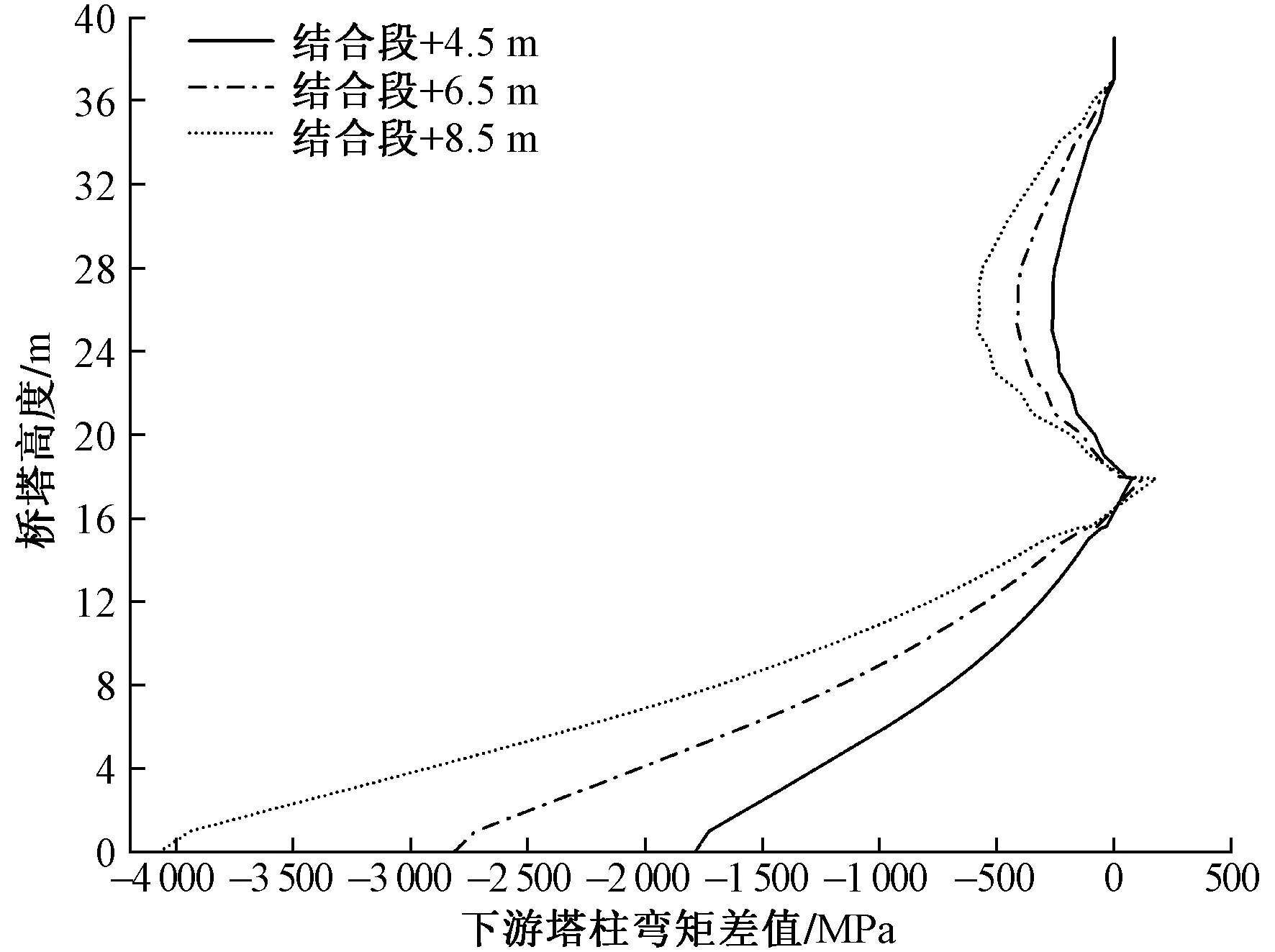
图3 结合段位置变化前后下游塔柱弯矩差值Fig.3 The difference of the bending moment of the downstream tower column before and after the position change of the joining section

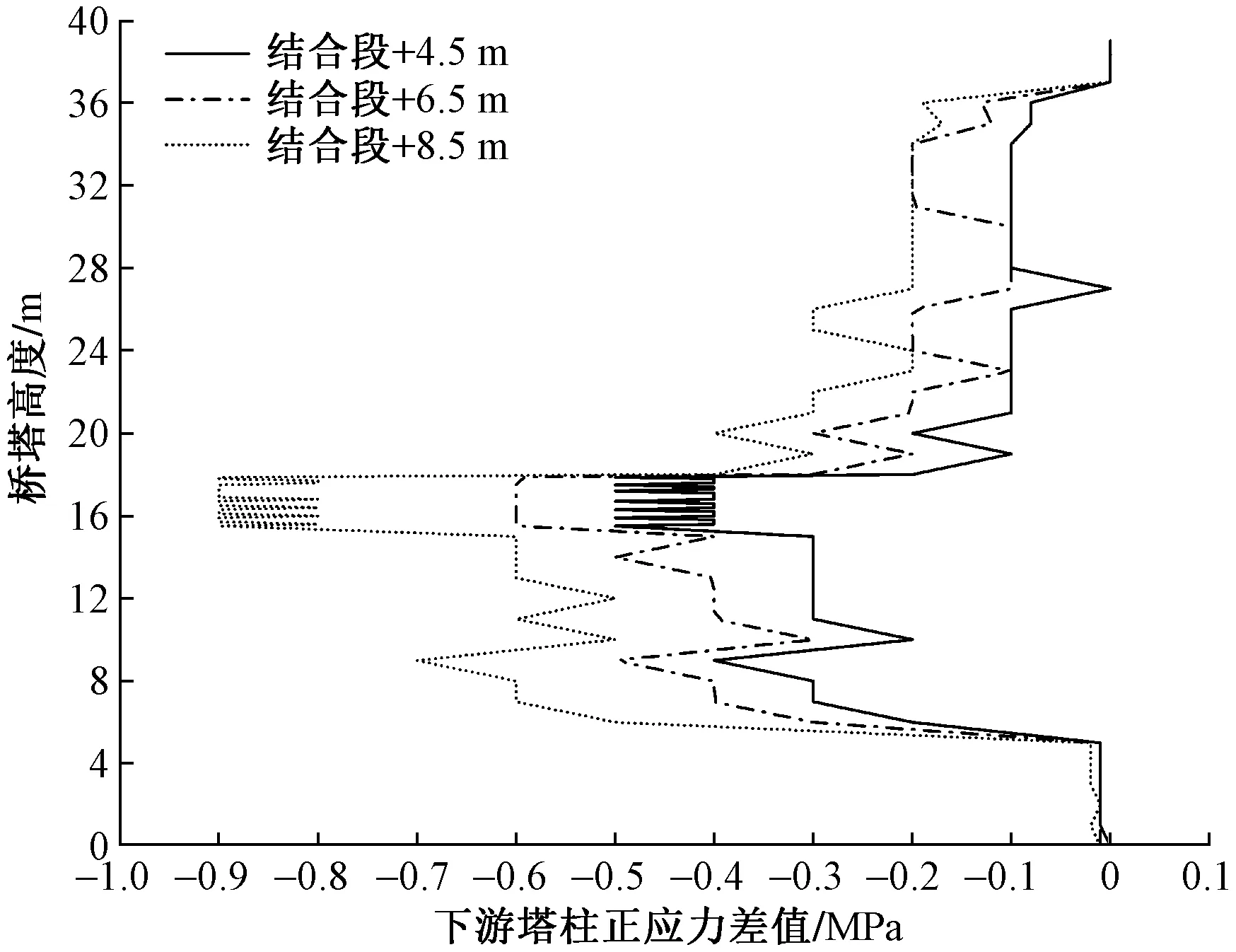
图4 结合段位置变化前后下游塔柱正应力差值Fig.4 The difference of the normal stress of the downstream tower column before and after the position of the bonding section changes

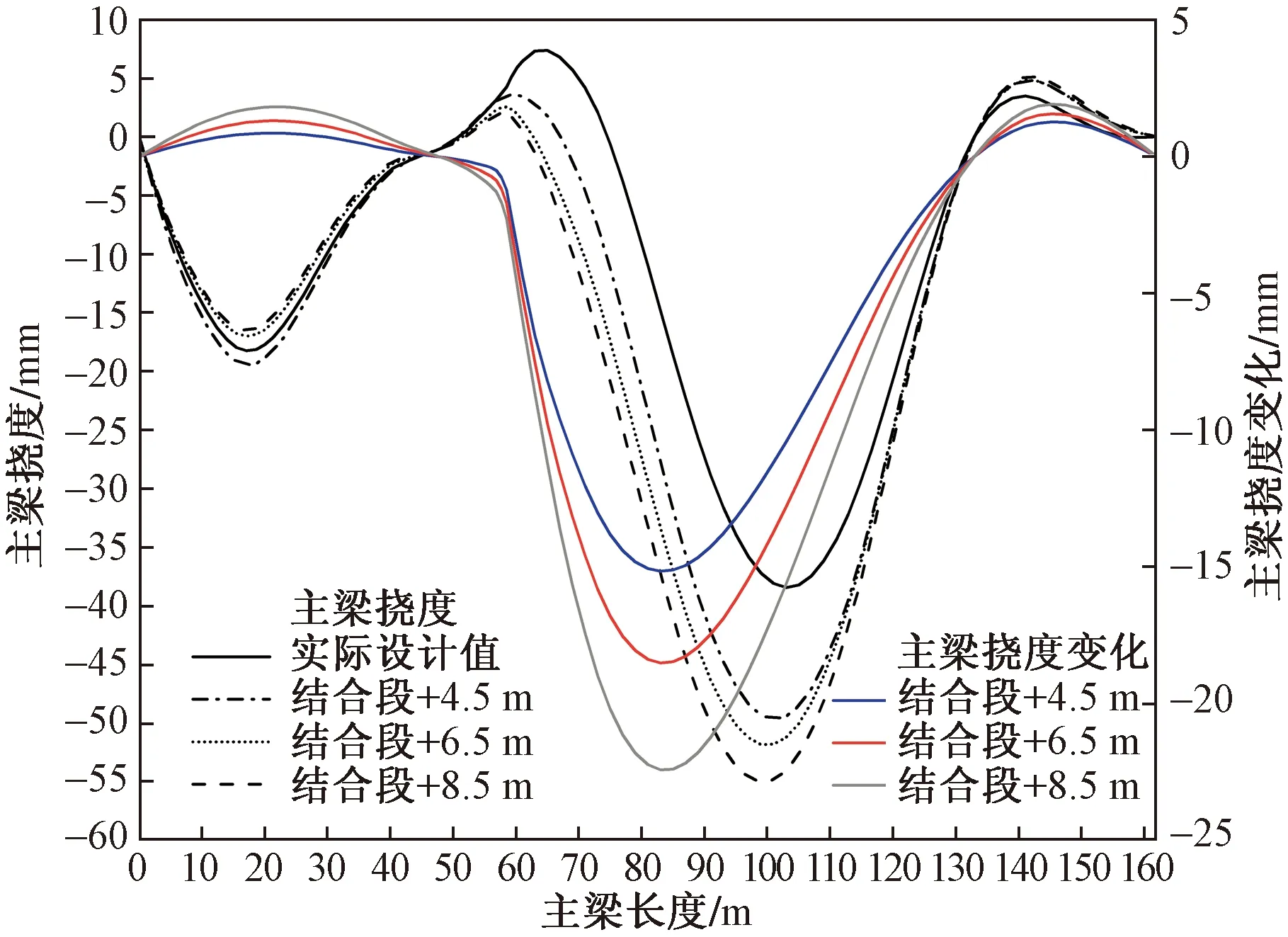
图5 结合段位置变化前后主梁挠度值和差值Fig.5 The deflection value and difference of the main girder of the right pylon before and after the position of the connecting section changes

图6 结合段位置变化前后下游塔柱纵向变形值和差值Fig.6 Longitudinal deformation value and difference of the downstream tower column before and after the position change of the combined section

表2 钢混结合段位置对于控制目标的敏感度Table 2 Sensitivity of steel-concrete joint position to control target

3.2 桥塔温度变化的影响分析

由于桥塔单向受阳光照射，桥塔背阳处和向阳处温度不均匀，产生日照温差，导致桥塔产生挠曲变形。而本桥桥塔在纵桥向和横桥向均采用异型曲线布置，属于典型的异型桥塔，在受到局部温差的影响时，桥塔的变形和受力问题更为显著，所以有必要对桥塔在受到局部温度荷载时进行模拟分析。以系统无局部温度荷载为基准，选取桥塔顺桥向前侧面局部升温20 ℃和桥塔顺桥向后侧面局部降温10 ℃两个工况进行计算，模拟桥塔的单面受阳光照射导致的温度不均匀情况，分别得到成桥状态下两种工况的主梁挠度和桥塔变形的改变量以及下游塔柱的弯矩值[13]。

图7～图9分别给出了在有限元模拟分析中，桥塔受到局部升温20 ℃和局部降温10 ℃后，桥塔的纵向变形和下游塔柱的弯矩值以及主梁的挠度变化。

从图7～图9的结果可以看出，成桥状态下，桥塔局部温度变化会对主梁和桥塔都产生一定程度的变形。局部升温20 ℃荷载下，主梁中跨主要产生下挠变形，挠度差值最大达到1 mm。桥塔纵向变形有所减小，纵向变形变化幅度最大值达到8.5 mm，下游塔柱弯矩增大，变化幅值最大达3 000 kN·m。局部降温10 ℃荷载下，主梁中跨主要产生上挠，挠度变化值最大为0.5 mm，桥塔纵向变形主要呈增长变化，变化幅度最大值达到4.2 mm，下游塔柱弯矩减小，变化幅值最大为1 500 kN·m。综上，桥塔局部温度荷载对主梁成桥线形影响较小，对桥塔成桥线形和桥塔下游塔柱弯矩影响较大。

表3 桥塔局部温度变化对于控制目标的敏感度Table 3 Sensitivity of the local temperature load of the pylon to the control target

图7 桥塔局部温度变化前后桥塔纵向变形值和差值Fig.7 The longitudinal deformation value and difference of the pylon before and after the local temperature change of the pylon

图8 桥塔局部温度变化前后下游塔柱弯矩值和差值Fig.8 The bending moment and difference of the downstream tower column before and after the local temperature change of the pylon

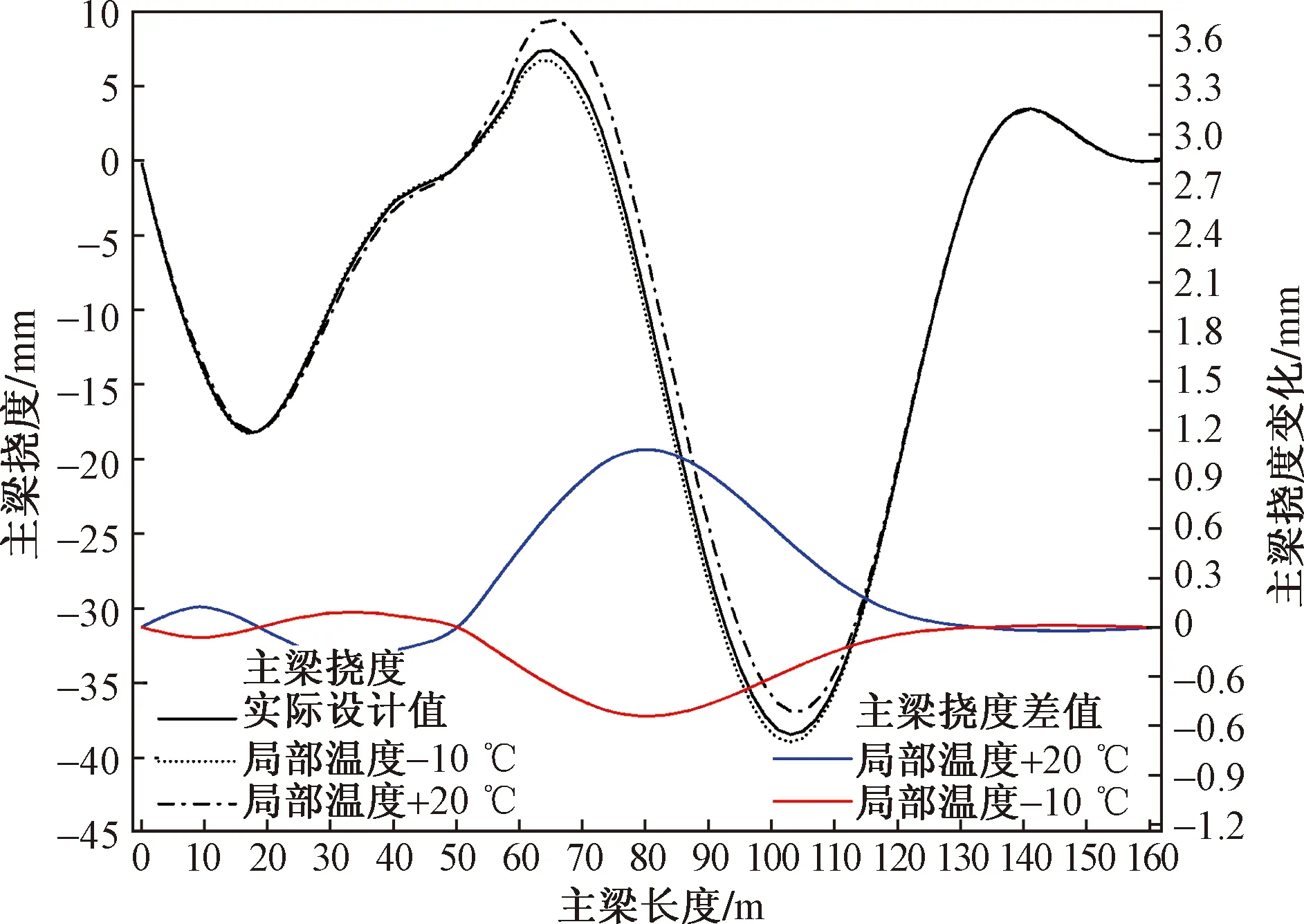
图9 桥塔局部温度变化前后主梁挠度值和差值Fig.9 The deflection value and difference of the main girder before and after the local temperature change of the bridge tower

表3列出了桥塔局部温度变化前后所选4个控制目标的数值，并根据式(2)、式(3)计算出敏感度。可以看出，塔顶纵向位移对桥塔局部温度的敏感度达到6.452，桥塔固结处弯矩、背索索力和主梁中跨跨中挠度对桥塔局部温度荷载敏感度都较低，当桥塔局部升温20 ℃时，塔顶纵向位移、主梁最大挠度和背索S1索力分别减小119.04%、减小4.16%和减小8.5%，桥塔纵向位移发生反向变形，当桥塔局部降温10 ℃时，塔顶纵向位移、主梁最大挠度和背索S1索力分别增加238.1%、增加1.35%和增加25.38%。由以上分析可得，桥塔局部温度荷载对桥塔线形影响较大，对桥塔弯矩和主梁线形基本无影响，对斜弯独塔斜拉桥结构设计需要注意桥塔纵向变形，特别是塔顶纵向位移。

3.3 斜拉索初拉力的影响分析

由于测量、温度变化、张拉技术的限制以及应力松弛等原因，桥梁斜拉索张拉时索力很难精确达到预定值，而且大桥运营过程中斜拉索的疲劳损伤也会导致斜拉索承载力变异，导致斜拉索承载力偏离正常设计状态，对结构产生重大的影响[14]。因此,将斜拉索初拉力分别增加和减少10%，将有限元模拟值与理性成桥状态下主梁挠度和桥塔纵向变形、下游塔柱弯矩进行对比，分析斜拉索初拉力偏差对斜弯独塔斜拉桥的影响。

图10～图12分别给出了在有限元模拟分析中，斜拉索初拉力增加10%和减小10%后，桥塔的纵向变形和下游塔柱的弯矩值以及主梁的挠度变化。

由图10可知，斜拉索初张拉力增大10%，会使主梁跨中发生上挠，边跨会出现些许下挠，同样斜拉索初张拉力减小10%，主梁跨中会发生下挠，边跨会出现些许下挠，挠度变化与初张拉力增大10%时基本成对称分布，线性最大改变量发生在跨中右侧，峰值达5 mm，影响程度在支座或桥墩附近较小在跨中部位附近变化幅度较大。

同样，斜拉索初张拉力变化前后，下游塔柱正应力也发生了较大变化， 由图11可知，在下游塔柱的上肢和下肢交接处正应力差值达到了4.5 MPa。

由图12可知，斜拉索初张拉力变化也对下游塔柱弯矩产生了较大的影响，尤其在桥塔与主梁连接处，弯矩变化值达到8 000 kN·m，从桥底到桥顶，弯矩变化的幅值也逐渐减小。由此可见，该类桥梁的成桥下的线形以及内力、应力分布对斜拉索初张拉力都较为敏感。

表4列出了斜拉索初拉力变化前后所选4个控制目标的数值，并根据式(2)、式(3)计算出敏感度。

图10 斜拉索初拉力变化前后主梁挠度值和差值Fig.10 The deflection value and difference of the main beam before and after the change of the initial tension of the stay cable

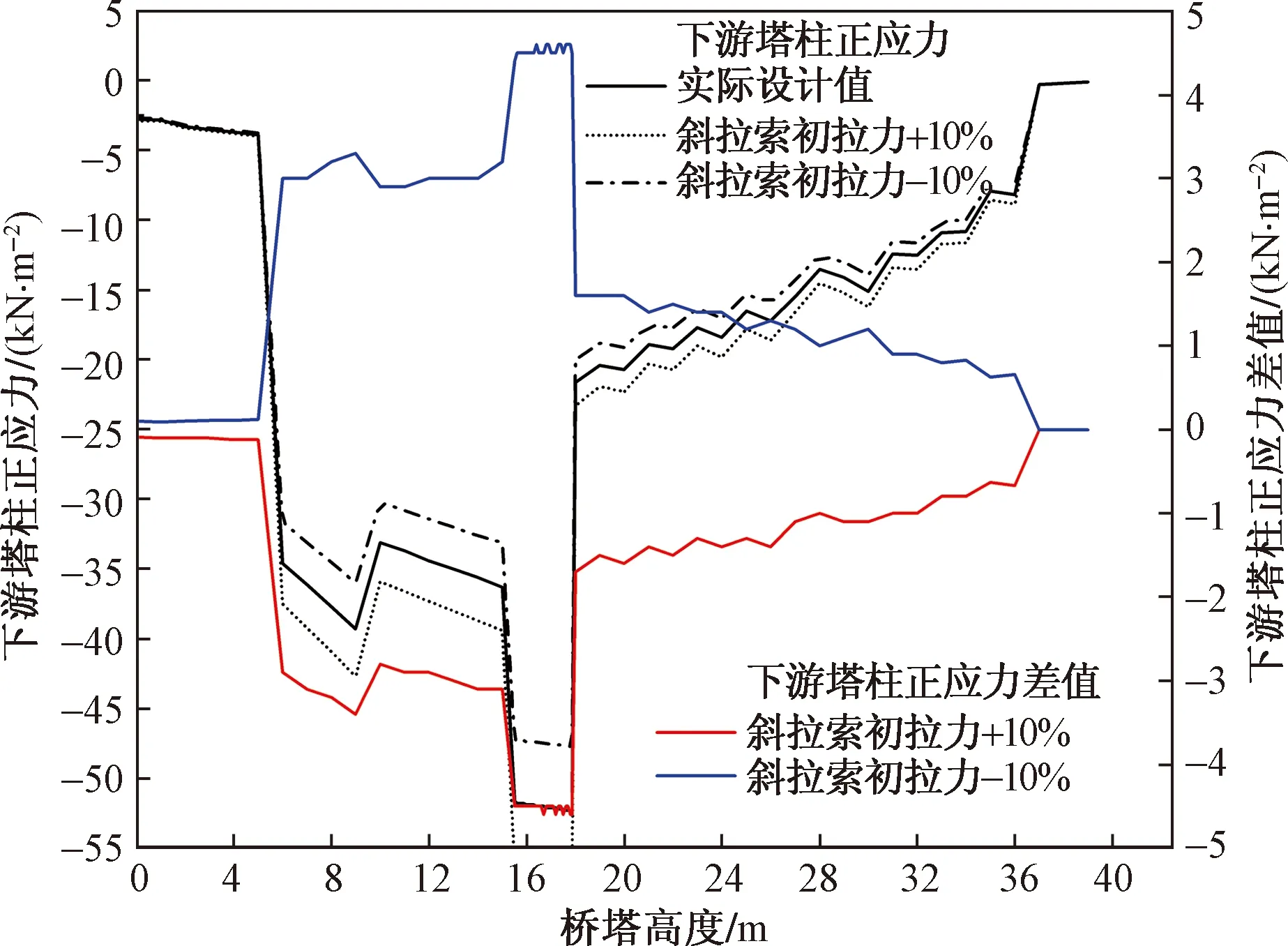
图11 斜拉索初拉力变化前后下游塔柱正应力值和差值Fig.11 The normal stress value and difference of the downstream tower column before and after the initial tension of the stayed cable changes

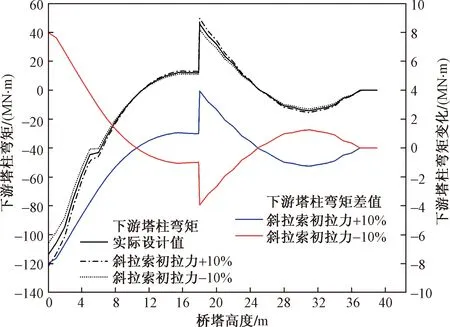
图12 斜拉索初拉力变化前后下游塔柱弯矩值和差值Fig.12 The bending moment and difference of the downstream tower column before and after the initial tension of the stayed cable changes

由表4结果可知，斜拉索初拉力对斜弯塔混合梁斜拉桥梁结构响应的影响程度从大到小依次为：塔顶纵向位移、跨中挠度、背索索力和塔梁固结处弯矩。其中，斜拉索初拉力每增加10%，塔顶纵向位移、主梁最大挠度、背索索力、塔梁固结处弯矩将分别减少67%，增加26%，减少9.4%，增加7%。由以上分析可以看出，斜拉索初拉力对塔顶位移和主梁挠度较为敏感，而其对背索索力和塔梁固结处弯矩影响较小，施工和成桥阶段桥塔顶点处位移要注意监控，背索索力也是重点监控对象。

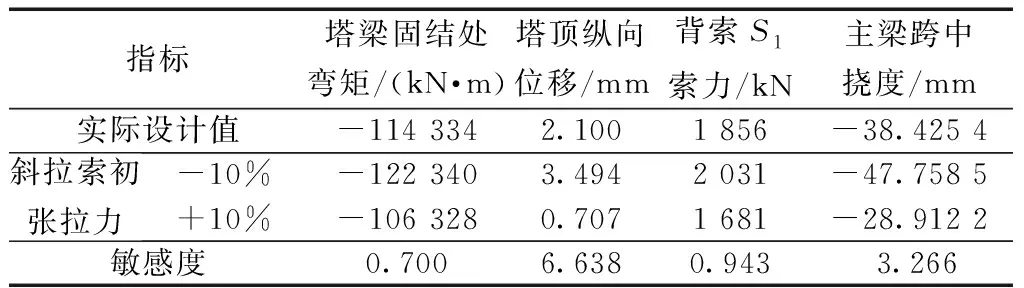
表4 斜拉索初拉力对于控制目标的敏感度Table 4 Sensitivity of initial tension of stay cables to control targets

3.4 背索倾角的影响分析

此桥桥塔为变截面斜弯钢塔，桥面宽幅达51 m，同时属于少背索体系，背索呈双向倾斜，背索倾斜角度关系到墩、塔、梁、索的受力是否能够达到最优状态，直接影响到斜拉索的合理索力分布，以及桥梁后期运营性能，所以有必要对背索倾角进行分析研究，确定此类桥梁对背索倾角的敏感性程度。选用背索竖向倾角来更明确地分析背索倾角对异型桥塔混合梁斜拉桥的影响程度[15]。背索竖向倾斜角度即背索在x-z平面上投影与主梁顺桥向的夹角(坐标系规定如图2所示)。

图13～图15给出了在有限元模拟中，通过改变背索在主梁上的锚固点位置改变背索竖向倾角时，桥塔下游塔柱的应力值和弯矩值及其变化值。由图13可知，无论背索竖向倾斜角度变大还是减小时，下游塔柱正应力值都出现增大，最大幅值可达到4.7 MPa，随着背索竖向倾斜角度增大，变化幅度减小，随着背索竖向倾斜角度减小，变化幅度增大。下游塔柱剪应力分别在桥塔钢混结合段和双肢交点处出现突变，变化幅度突出，在进行结构设计和运营监测时需要重点关注。由图14可知，桥塔剪应力值变化不大，最大变化值达1.55 MPa，在钢混结合段处发生突变后，变化幅度呈减小趋势。由图15可知，弯矩值在桥塔高9 m处，差值出现交叉变化，从正增加变成负减小，同样在双肢交点处突变后，变化幅度开始减小。

图13 背索竖向倾斜角度变化前后下游塔柱 正应力值和差值Fig.13 The normal stress value and difference of the downstream tower column before and after the vertical inclination angle of the back cable changes

图14 背索竖向倾斜角度变化前后下游塔柱 剪应力值和差值Fig.14 The shear stress value and difference of the downstream tower column before and after the vertical inclination angle of the back cable changes

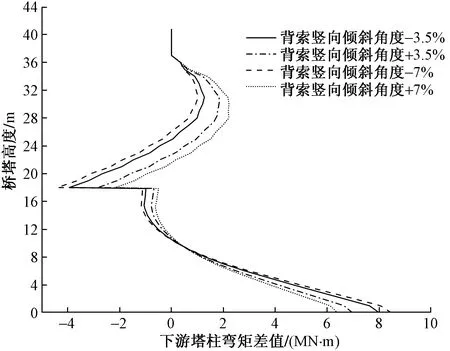
图15 背索竖向倾斜角度变化前后下游塔柱弯矩值和差值Fig.15 The bending moment and difference of the downstream tower column before and after the vertical inclination angle of the back cable changes

由表5可得，桥塔线形和主梁线型对背索竖向倾斜角度的敏感较高，其中，背索竖向倾斜角度变化3.5%，塔顶纵向位移、主梁最大挠度将较理想成桥状态最大变化达102.6%和30.1%。背索竖向倾斜角度变化7%，塔顶纵向位移较理想成桥状态最大变化也达到205.8%，主梁最大挠度将较理想成桥状态变化70.2%。但在背索竖向倾斜角度变化的过程中，背索索力和塔梁固结处弯矩变化并不明显，所以敏感度不高。由以上分析可以看出，塔顶位移和主梁挠度对背索竖向倾斜角度较为敏感，而背索索力和塔梁固结处弯矩对背索竖向倾斜角度敏感度不高，施工过程中要严格选取背索的合理倾斜角度，后期运营过程中也要考虑对桥塔顶点和主梁跨中挠度重点监控，塔柱双下肢交叉处也要重点监控。

表5 背索竖向倾斜角度对于控制目标的敏感度Table 5 The sensitivity of the vertical inclination angle of the back cable to the control target

4 结论

对某异型桥塔混合梁斜拉桥建立空间几何有限元模型，通过引入敏感性指标，分析不同参数对成桥状态下斜拉桥的影响程度，得出如下结论。

(1)主梁线形和桥塔纵向变形对钢混结合段位置的敏感度较高，但塔梁固结处弯矩和背索索力的敏感度较低，所以在设计阶段，钢混结合段的位置的选取尤为重要。

(2)桥塔局部温度荷载对桥塔线形的影响显著高于对桥塔弯矩的影响，对主梁线形和塔梁固结处的影响可以忽略。在设计过程中要充分考虑局部温度荷载的影响，合理地选取对局部温度荷载敏感度高的关键构造参数，保证桥梁运营的安全性。

(3)成桥状态下桥塔线形及主梁竖向挠度对斜拉索初拉力较为敏感，在施工阶段中要严格控制斜拉索初拉力的的精度，保证索力的合理性和安全性，避免因索力变异和施工误差对桥梁后期运营过程产生安全问题。

(4)背索竖向倾斜角度在斜弯独塔斜拉桥中较为显著，其对主梁和桥塔的线形以及桥塔受力和背索拉力均有较大影响，是控制斜拉索结构整体平衡和桥塔局部平衡的重要构件，在设计阶段，要考虑桥塔的合理受力，严格选取背索的合理倾斜角度。