三维数值流形法覆盖系统并行分区生成算法
潘帅琪, 张亚军, 张友良, 刘哲亨
(海南大学土木建筑工程学院, 海口 570228)
数值流形法(numerical manifold method,NMM)是Shi[1-2]提出的一种能够统一求解物体的小变形开裂以及分析非连续大位移的新数值方法。这种数值方法能够模拟物体从连续到非连续状态的全过程。NMM是将有限单元法(finite element method,FEM)和非连续变形分析(discontinuous deformation analysis,DDA)统一起来的推广,在计算非连续面的滑动、开裂等问题上具有独特优势,适宜求解自由初边值问题。尽管二维NMM目前已经在诸多领域得到了广泛应用[3-6],但三维NMM作为明显更符合实际工程问题的方法,受限于接触判断和计算效率上遇到的瓶颈,目前使用三维NMM进行计算的算例规模都相对较小[7-9]。
目前三维NMM多采用六面体或四面体网格生成数学覆盖系统,流形单元的生成过程较二维更复杂。且与二维NMM相比,三维NMM具有更复杂的接触判断和单个流形元更多的自由度。三维NMM在求解过程中,需要计算的整体刚度矩阵的维数也较二维高,在相应时间步内还有大量耗时的迭代、接触判断过程,而在每一次的开闭迭代中都需要进行方程组的求解。在模型较大时,如果时间步过小,数学网格设置过大则其收敛性难以保证,需要设置合适的网格大小以及设置较小的时间步使精度满足工程需求;而且NMM的局部覆盖位移函数由于使用全局坐标的多项式形式,导致积分项阶次提高以及自由度增大,虽然相较于FEM提高了计算精度,也使得NMM的计算量增大。这都使得程序的运算时间大幅增加。接触判断和计算效率问题成为三维NMM研究应用的关键性问题,在接触判断方面,石根华新提出的EAB(entrance block between block A and B)理论可初步解决目前三维NMM在接触判断方面面临的困境。然而,EAB理论的引入也使得接触判断的计算量增加,因此亟需有效算法提升三维NMM的计算效率。
由于硅材料以及微观尺度的限制,目前摩尔定律已逐渐失效,单个CPU主频已很难获得较大的提升,从软件角度提升计算机的计算能力成为研究热点。并行计算是一种强大的计算工具,能够发挥多核CPU计算机或计算机集群优势,充分利用计算机资源,加快计算速度。在工程数值计算模拟仿真领域,大量研究人员正在使用并行计算技术来提升计算能力和扩大计算规模[10-14]。将并行计算技术引入三维NMM覆盖系统生成程序,可以有效提高三维NMM的整体计算速度。
在三维NMM覆盖系统串行生成算法方面,已有多位学者提出了生成算法。李海枫等[15]利用块体切割技术,实现了三维NMM流形单元的生成;杨石扣等[16]采用六面体数学网格覆盖问题域,然后将复杂块体与六面体网格进行布尔交运算, 进一步生成流形单元和物理覆盖。柯锦福等[17]运用布尔运算实现了简单的三维块体切割功能,将四面体网格与问题域进行布尔交运算得到流形块体;李伟等[18]、伍书重等[19]对三维NMM覆盖的生成算法及其改进进行了研究。张友良等[20]使用MPI(message passing interface)对二维NMM覆盖系统并行生成算法进行了研究。对于三维NMM覆盖系统并行生成算法则尚未有学者开展相关研究工作。并行计算的工具有很多种,如MPI、OpenMP、OpenACC等。其中MPI适用于粗粒度并行计算[21],不仅可用于多核计算机,且可应用于机群系统进一步扩大计算规模。由于本三维数值流形法程序基于Windows系统开发并采用C++编写,使用MSMPI(Microsoft MPI)实现三维数值流形法覆盖系统生成的粗粒度的并行化是比较合适的方案[22]。
鉴于此,基于布尔运算的三维NMM覆盖系统串行生成算法的基础上,借鉴二维NMM覆盖系统并行生成算法思路,对三维NMM覆盖系统并行生成算法展开研究。主要研究三维NMM前处理过程中覆盖系统、流形单元的并行生成算法,以及基于分布式内存并行编程模式下覆盖系统生成中界面数据传递算法,为后续的接触判断、方程组求解等模块的并行计算提供并行前处理器。
在基于布尔运算的三维NMM覆盖系统串行生成算法基础上,用分布式存储系统的MPI编程接口将三维数值流形法前处理的串行程序改为并行程序,实现了三维NMM覆盖系统的并行生成,为后续三维NMM应用于大规模实际工程数值模拟开展基础研究工作。
1 基于布尔运算的三维数值流形法覆盖系统生成算法

基于布尔运算的三维NMM覆盖生成算法中,定义在同一个数学覆盖内的流形单元,如果两个流形元的交集为数学面,则此数学面为这两个流形元的公共数学面。物理覆盖根据“在覆盖问题域的一个数学覆盖内,彼此有公共数学面的流形元并集形成一个物理覆盖”。对于所使用的六面体数学网格,所生成的每个流形单元应当与8个物理覆盖相关联。可据此检查物理覆盖是否生成正确。
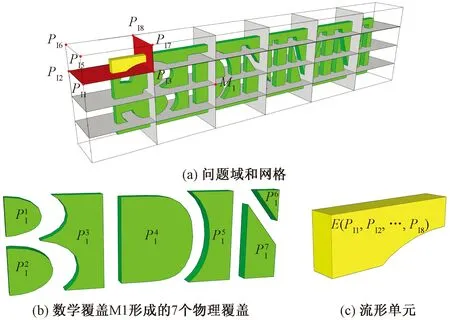
图1 三维NMM的覆盖系统和流形单元Fig.1 Covers and manifold elements for 3D-NMM
本文算法中一个数学网格与体模型进行布尔交运算生成流形单元的过程主要步骤如下。
步骤1将数学网格与物理模型进行面面相互求交,得到物理交线集合,物理线和数学线进行迹线求交得到数学、物理有向边集合。
步骤2将六面体数学网格分别与物理模型进行块体布尔交运算,将两个求交块体的各个面分割成许多个小面,若有向面的线段中有数学线即为数学面,否则就为物理面,同时根据面的坐标及法向量确定需要删除的面。
步骤3求各个面的法向量,按照空间块体搜索的最大右转角准则[23]形成块体。
步骤4三维流形单元块体生成后,通过几何运算寻找每个流形单元关联的数学覆盖。
在三维流形块体生成后,根据Shi[24]提出的三维块体拓扑性检查方法,对所有任意形状的多面体进行有效性检查,如果能够满足:
∂(∂Bi)=0
(1)
(2)
式中:Bi为三维多面体;T为目标体外边界。
本文方法中物理覆盖的搜索生成是通过每个数学覆盖进行的,在生成物理覆盖的过程中不会相互影响,在并行程序中便于界面物理覆盖生成以及与界面流形单元相关联。用这种方法生成物理覆盖时需要先生成流形单元,在形成物理覆盖的同时,可确定跟某个物理覆盖关联的所有流形单元以及生成物理覆盖的数学覆盖。整体物理覆盖的生成过程如图2所示。

图 2 物理覆盖系统生成流程图Fig.2 Generating flow chart based on physical coverage system
程序中三维数学覆盖、三维物理覆盖和三维流形单元分别用MathCover3D、PhysicalCover3D和Manifold Element3D三个类来定义,基于分区计算算法的子区域用SubDomain3D类定义。这4个类之间的关系如图3中UML类图所示。在MathCover3D类中,_pc3D和_me3D分别表示此数学覆盖所包含的物理覆盖和流形单元。 PhysicalCover3D类中,_mc3D表示此物理覆盖位于此数学覆盖当中;并且该物理覆盖与_me3D容器中所存储的流形单元相关联。在ManifoldFlement3D类中,_pc3D表示与该流形单元相关的物理覆盖,_mc3D表示与该流形单元相关的数学覆盖。子区域中的_intfPc3D表示界面物理覆盖,_intfMe3D表示界面流形单元,界面物理覆盖与界面流形单元用于计算过程中区域间数据交换。

图3 三维数值流形法数学覆盖、物理覆盖、流形单元及子覆盖区UML类图Fig.3 UML graph of math cover3D,physical-cover3D,manifold element3D,and SubDomain3D
2 三维NMM覆盖系统并行生成算法
三维NMM覆盖系统生成串行算法与并行算法主要不同点前节已经阐述,以下将对这些不同点及对应的处理算法进行介绍。
2.1 并行任务分配与子计算区域划分
粗粒度并行编程模式下覆盖系统生成的核心是计算区域划分。对于基于六面体数学网格生成数学覆盖的三维NMM,采用分区覆盖生成方法,并考虑2个并行算法重要约束条件:一是处理器负载基本均衡,即各个处理器分配的区域大小相似,最优利用硬件资源,避免部分处理器处于闲置状态而增加等待耗时;二是子区域边界接触面尽量小,降低界面单元数量,从而减少处理器间通讯耗时,降低程序并行过程中数据传递消耗,进一步提升并行计算速度。
在三维NMM并行算法上采用分区计算方法来实现覆盖系统的并行生成,将体模型在不同处理器上分别对体模型不同范围区域的覆盖系统进行生成,在生成流形单元时各个子区域内的数学网格同时与体模型进行布尔交运算来生成,把整个模型覆盖系统生成任务分解为不同的子区域上覆盖系统生成任务,然后不同处理器负责不同计算区域的覆盖系统的生成,最后通过界面单元信息传递实现区域间的数据交换,实现三维NMM覆盖系统的并行生成。子计算区域生成的具体算法实现过程如下。
SubDomain3D生成算法1具体步骤如下。
步骤1输入体模型几何数据。
步骤2根据模型几何数据计算模型的问题域尺度。
步骤3用粗六面体网格覆盖模型域。
步骤4检查六面体网格是否至少有一个顶点在模型范围内,去除在模型边界外的六面体网格。
步骤5对与模型边界相交或在模型内部的六面体网格进行子区域划分。
步骤6合并分配到不同处理器的网格,得到子区域。
图4~图6为算法1的过程说明。其中,图4为一个边坡问题的模型,图5为用粗六面体网格覆盖模型后的图形,图6为图4与图5叠加,然后去掉与问题域不相交的粗六面体网格后的图形。粗六面体网格不同于数值流形法中的数学网格,它比数学覆盖网格要大。用大小相等的粗六面体网格覆盖问题域的目的是之后利用划分工具得到负载基本均衡的子计算区域。步骤5中子计算区域划分通过调用METIS库的网格分区函数来实现, Metis是由Karypis Lab公司开发,可用于划分不规则图、网格,具有高质量的划分结果。其命令行程序模式也方便集成到C++程序中。另外METIS具有很低的注入元(fill-in),从而降低了存储负载和计算量。该软件能够很好地满足粗粒度模型级并行计算中区域划分的基本约束条件,即处理器负载基本均衡和不同处理器之间通讯数据量最小的两个条件[25],是科学并行计算中的重要的分区工具。三维数值流形元的数学覆盖是规则的六面体网格,每个网格大小相等,因此子区域的计算量与其单元数量近似成正比。使用函数METIS_PartMeshDual对粗网格进行子计算区域划分,即可得到基本计算量均衡的子计算区域。在METIS manual中可以了解该函数的详细使用规则。

图4 边坡问题模型Fig.4 Boundary of the slope problem

图5 粗六面体网格Fig.5 Coarse hexahedron grids
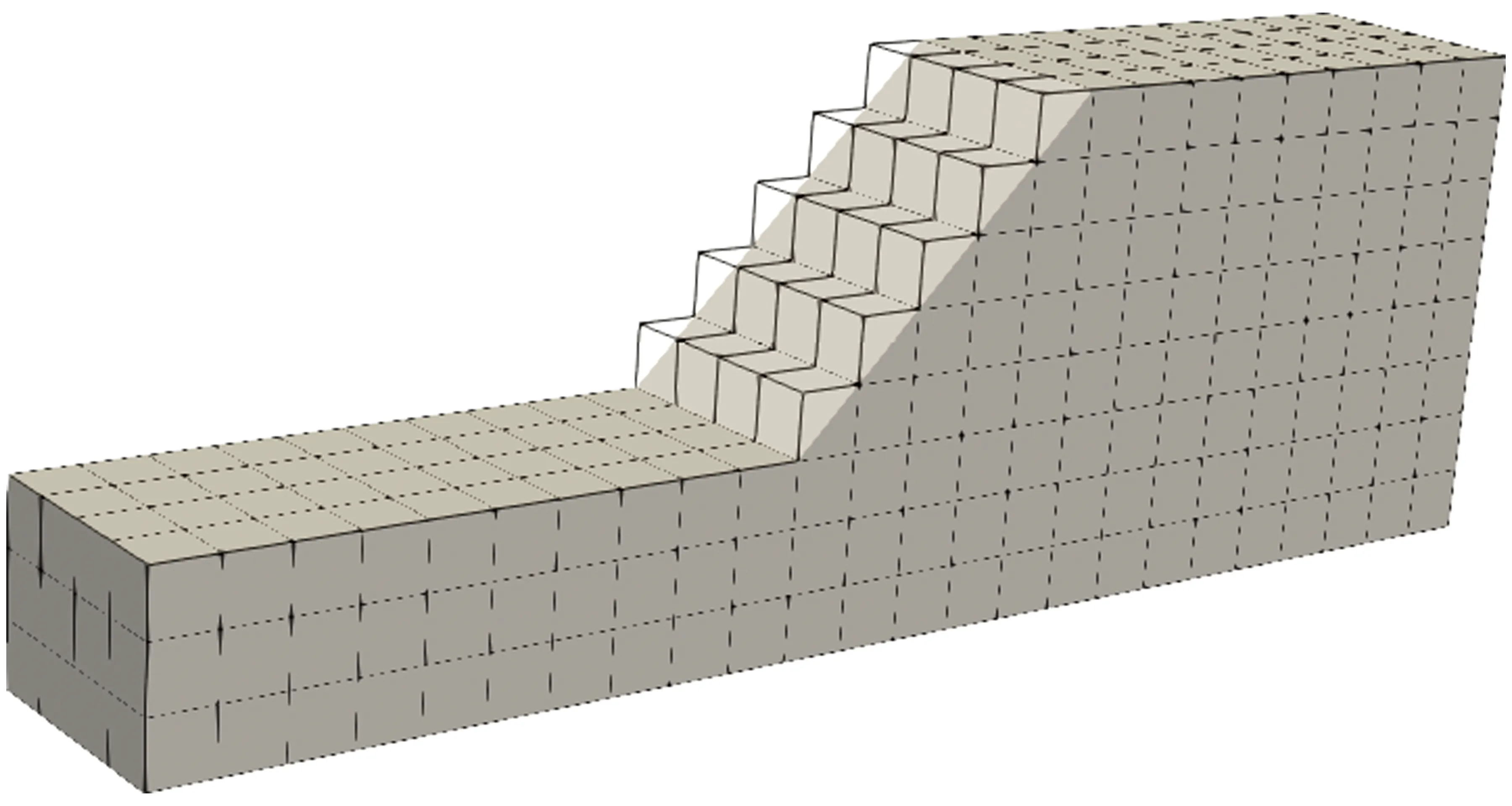
图6 参与划分的粗六面体网格Fig.6 Hexahedral mesh that participates in the partition
图7为算法1中步骤5中使用METIS划分后形成的4个子计算区域网格图形的结果。各个子区域合并形成整体覆盖区域(图8)被子计算区域间共享的面称为子计算区域间的相邻界面, 相邻界面在随后的界面元素的确定及区域数据传递非常重要。将子计算区域几何信息发送至各个处理器,每个处理器负责体模型各自计算区域范围内的覆盖系统以及流形单元生成。

图7 子区域划分结果Fig.7 SubDomain3D interval partition results

图8 由各个子区域形成的整体区域Fig.8 The whole region formed by each subdomain

图9 子区域数学网格Fig.9 Mathematical grids for a subdomain
2.2 三维NMM子计算区域覆盖系统生成算法
每个区域内的数学覆盖与串行相同,其生成可重复使用串行算法的代码。但要注意在布置子区域数学网格时,要求所有子区域数学网格大小相同,并采用相同参照点,以免在子区域界面处出现网格不协调情况。
在子区域数学覆盖系统生成过程中, 各个子计算区域的数学网格应当在完全覆盖本子计算区域的同时外扩一圈,如图9所示。如果在布置子区域的数学网格时将数学覆盖范围完全限制在子计算区域内,则不便于后续三维NMM算法程序中界面单元的确定。另外,在与体模型进行布尔交运算生成各个子区域的流形元时,需要先判断数学网格是否在子区域范围内,只有在子区域范围内的网格需要与体模型相互求交生成三维流形单元。除此以外,三维NMM覆盖系统的并行生成算法代码与串行生成算法代码基本相同。图10为边坡模型覆盖系统和流形单元的在并行算法下的生成结果。在覆盖系统和三维流形单元生成后,即可根据覆盖系统信息确定UML类图(图3)中SubDomain3D的类中成员:数学覆盖(_mc3D)、物理覆盖(_pc3D)和流形单元(_me3D)。
2.3 三维NMM子计算区域界面信息建立算法
三维NMM覆盖系统并行算法数据通信交换中包括3个基本概念:一是子区域相邻界面,指一个子区域与其他子区域间相邻的边界面,如图11中直线所指的界面;二是界面物理覆盖,指被多个子区域共享的物理覆盖;三是界面流形单元,指包含界面物理覆盖的流形元,这部分流形元与其他子区域流形元共享一些物理覆盖。
界面物理覆盖属于2个或以上子计算区域。为实现计算过程中不同区域间数据传递,界面信息搜寻算法详细过程见如下算法2。算法2中步骤1被标记为INTERFACE_Node_notConfirmed的数学覆盖部分仅是位于区域外部边界处的数学覆盖,因此在步骤2中通过处理器间相互通信确定真正的界面数学覆盖。获得的界面物理覆盖和界面流形单元分别保存在子计算区域成员变量_intfpc3D和_intfme3D中。
界面信息生成算法2步骤如下。
步骤1对数学覆盖循环,依据数学覆盖与子区域边界几何关系,搜寻界面数学覆盖,标记为INTERFACE_Node_notConfirmed。
步骤2子计算区域与相邻子区域相互通信,通过数学覆盖几何信息,得到与其他计算区域相邻界面处的真实界面数学覆盖集合,更新标记为INTERFACE_Node。
步骤3将状态为INTERFACE_Node的界面数学覆盖中的流形元标记类型为界面流形单元。
步骤4在同一界面数学覆盖中的界面流形单元,按照前述物理覆盖生成办法生成该数学覆盖内的物理覆盖,并标记状态为界面物理覆盖。

图10 并行算法下生成的覆盖系统和流行单元Fig.10 Cover systems and manifold elements generated by parallel algorithm
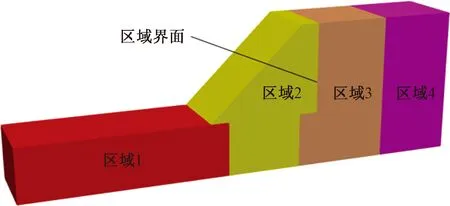
图11 子区域界面Fig.11 Subdomain3D interfaces
本文算法2通过对图10中子计算区域覆盖系统和流形单元的进一步处理,得到的界面流形单元如图12所示。

图12 区间界面流形单元Fig.12 Interface manifold elements between different regions
在本算例中,区域1生成流形单元1 056个,区域2生成流形单元1 040个,区域3生成流形单元1 064个,区域4生成流形单元1 024个,平均1 046个,各个区域内流行单元数量与均值相差很小,区域间最大差值为40,相交于流形单元总体数量是十分小的数量。说明本并行算法的区域负载是基本均衡的。
3 算例
2.1节中给出了一个简易边坡模型的算例。给出一个大型边坡工程覆盖系统的并行生成算例,几何模型的示意图如图13所示。图14为采用不同计算核心得到的模型和子区域覆盖系统。

图13 问题域模型Fig.13 Problem domain model
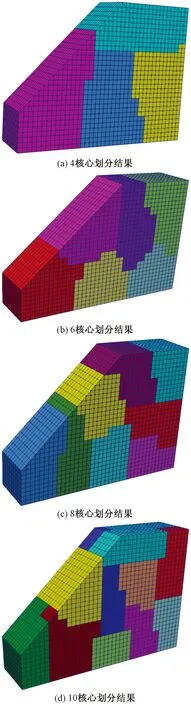
图14 不同核心下生成的覆盖系统和流形单元Fig.14 Covering systems and manifold elements produced under different number of processors
图15为不同核心情况下至界面单元计算完成后的计算时间对比,通过比较可知,三维数值流形法并行算法的实际加速效果并不与核心数成线性关系,没有完全达到理想加速效果。其主要原因有:①并行计算过程中,各个处理器计算量不均匀导致其他处理器等待问题;②随着核心数及划分区域增多,界面单元数学增加,处理器之间数据通讯传递耗时增加;③目前本算法在进行区域划分时未考虑区域内节理对计算效率的影响,导致含节理区域流形单元数目较其他区域多,这个因素将在后续并行算法研究中结合METIS网格权重功能对含节理区网格识别并增加划分权重,进一步实现区域划分的平衡性。
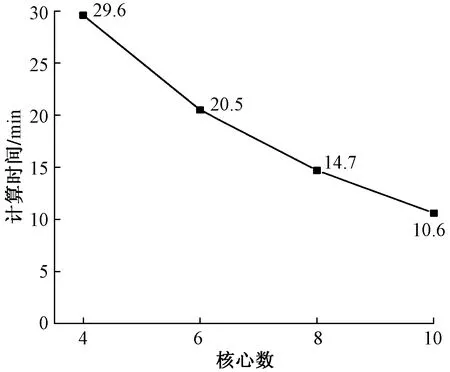
图15 不同核心情况下计算时间Fig.15 Computation time with different number of CPU
图16为4种不同分区情况下下各子区域流形单元个数,可以看出,4核心下区域间流形元最大差值为144,6核心下区域间流形元最大差值为158,8核心下区域间流形元最大差值为106,10核心下区域间流形元最大差值为78,无论哪种划分方式,各个子区域的流形元个数均差别较小,且随着划分区域的增多,其差值总体越来越小。说明本并行覆盖生成方法具有较好的负载均衡性。
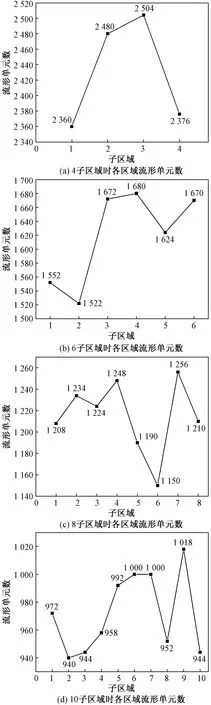
图16 不同分区情况下各区域流形单元数Fig.16 Number of manifold elements in each region under different partition conditions
4 结论
三维NMM覆盖系统并行生成算法只需要输入体模型几何数据,这些数据与串行算法过程中数据输入方法完全相同。同时,本文并行算法输出的三维NMM覆盖系统数据可以直接传递至后续三维NMM计算求解器计算,是高效的粗粒度模型级并行算法。
(1)在基于布尔运算的三维NMM覆盖系统生成算法上,研究了粗粒度并行下三维NMM覆盖系统生成算法,并取得了预期的加速效果,结果表明,该并行计算策略加快了三维NMM覆盖系统的生成速度,而且能够适应各种规模的问题。
(2)三维NMM覆盖系统并行算法中保证各个处理器计算任务的负载基本均衡可以提高程序运行效率,充分利用并行优势与计算机硬件资源。
(3) 三维NMM覆盖系统生成算法中计算量最大的是流形单元生成,利用分区覆盖生成方法可实现三维NMM覆盖系统的并行化生成,是高效的基于粗粒度分布式内存编程模式下的并行算法。
(4)如何设计能快速确定界面单元的算法至关重要,界面信息用于后续计算过程中数据交换和数据通信。
本文算法是针对计算模型进行基于区域分解思想的粗粒度并行算法。针对三维NMM计算中方程组的求解进行算法级的细粒度并行数值方程求解还需进一步的研究。另外,云计算计术是当今兴起的技术热点,可以为用户提供弹性计算资源,用户可以根据自身需求创建使用不同配置的虚拟主机或计算机节点集群来进行计算。为了三维NMM的进一步推广应用,结合云计算技术与三维NMM并行数值求解是下一步需要进行的研究工作。

