一种新的基于特殊离群样本优化的三维点云特征选择算法

黄 祥，王红星，顾 徐，孟 悦，王浩羽

一种新的基于特殊离群样本优化的三维点云特征选择算法

黄 祥，王红星，顾 徐，孟 悦，王浩羽

(江苏方天电力技术有限公司，江苏 南京 211102)

随着元宇宙、数字孪生、虚拟现实与增强现实等前沿技术的快速发展，三维点云在电力、建筑、先进制造等行业中得到广泛应用，随之而来的，如何降低三维点云数据冗余度、有效进行点云特征选择，已在充分利用海量点云数据中扮演着关键角色。考虑到现有大多数三维点云特征选择算法忽略了特定样本在特征评估中的表现，提出一种新的有监督特征选择算法，即基于特殊离群样本优化的特征选择算法(FSSO)。具体地，为获得精准的特殊离群样本(SOs)，FSSO优化均值中心并动态地界定类簇主体；计算SOs的类内相对偏离程度，通过减小类内相对偏离对特征进行打分，实现特征选择过程。在3个公共的三维点云模型分类数据集上(ModelNet40，IntrA，ShapeNetCore)的实验，以及4个高维人工特征数据集的验证实验结果表明，相较于其他特征选择算法，FSSO可选择出具有更强分类能力的特征子集，并提升分类准确率。

三维点云数据；有监督特征选择；特殊离群样本；类内相对偏离程度；分类

三维点云数据分析旨在从无序、非结构化的三维数据中解构出有用信息，是机器学习和计算机视觉领域中的热点问题[1-2]。在诸如元宇宙、数字孪生、数字城市、虚拟现实等现实应用中，不同技术手段获取的三维点云数据往往含有大量冗余特征，增加了点云数据分析和解读的难度。特征选择是从原始特征集中选出有识别力的特征子集，不仅可以有效地降低数据维度，还能提升对样本的表征能力，是点云数据分析的有效手段。

根据是否依赖样本的类别标签，特征选择算法可以分为：有监督、无监督和半监督特征选择[3]。有监督特征选择方法又可以进一步划分成过滤式、包裹式和嵌入式。其中，过滤式模型不依赖任何分类器的表现，通过衡量训练样本的本质属性对各特征进行评分，因此计算效率很高。包裹式模式基于随机搜索序列，需要依据分类结果选择得分最高的特征子集，故计算量较大。嵌入式模型将特征选择问题与分类问题结合成单一目标规划问题，虽然相较于包裹式模型，其计算成本大大降低，但仍不及过滤式模型。考虑到三维点云数据含有丰富的内在属性，且数据规模较大，因此本文设计采用过滤式模型的特征选择算法。

此外，大多数特征选择算法将数据库中的每个样本均视为同等重要。但在实际应用中，某些特定样本如离群(outliers)，往往隐含更有价值的信息待挖掘。如图1所示，类别“aneurysm”(记为类别1)中有一些样本，如1(k1)，表现为远离所属类内大多数样本，却进入到了类别“blood vessel”(记为类别2)中。显而易见，从信息论的角度而言，相较于普通样本2(k1)，形如1(k1)这类特殊离群样本信息熵大，含有更多有价值的信息，理应在特征选择过程中获得更多关注。

通过上述分析可以发现，为实现基于特殊离群优化的特征选择算法，需解决如何准确地获取特殊离群样本(specific outliers，SOs)和基于SOs的特性进行特征选择2个问题。本文基于SOs表现，提出了一种有监督、滤波式的，基于特殊离群样本优化的特征选择(feature selection based on specific outliers，FSSO)算法。首先，相较于常见的类均值中心，FSSO采用去除部分离群样本后，计算剩余样本的均值作为优化的类中心；然后，利用该优化的均值中心，计算各类中的SOs；最后，计算SOs的类内相对偏离程度，并引进具有统计意义的样本正态分布3原则作为可调节阈值，将超过阈值的大片特征视为冗余特征，从候选特征集中筛除。基于3个不同类型的大规模点云模型数据集(ModelNet40，IntrA，ShapeNetCore)，以及4个高维人工特征数据集的对比实验发现，本文提出的FSSO算法相比其他特征选择算法，能够选出有较强识别力的特征子集、并提高了分类准确率。

图1 三维点云分类数据集IntrA中的特殊离群样本x1(k1)

1 相关工作

1.1 三维点云数据处理

随着深度学习的发展，出现了许多使用深度神经网络进行点云分类的工作。CHARLES等[4]提出的PointNet是将多层感知机用于点云分析，但其无法获取完整局部特征信息及学习邻接点间关系。QI等[5]随后提出的PointNet++则解决了提取点云局部特征的问题。后续研究者继续提出了更多的基于PointNet++框架的点云分类网络，其中代表的工作有PointWeb[6]，So-Net[7]和Grid-GCN[8]等。

本文的工作是基于三维点云特征选择，因此实验时只使用点云分类网络中的特征提取层的输出作为后续特征选择算法的输入。点云特征提取有CurveNet[9]网络，其连接点(曲线)序列首先通过点云进行引导式步行分组，然后再重新聚合以增强其逐点的特征。3DMedPT[10]是专门针对医疗点云的基于注意力的深度网络模型，在查询中增加上下文信息和总结本地响应，并在注意力模块中捕获本地上下文和全局内容特征交互。DGCNN[11]中的EdgeConv可以在保持点云排列不变性的情况下，提取点云局部形状的特征。

然而，通过深度神经网络从三维点云数据中提取的高维特征不可避免包含冗余特征，会直接影响分类的准确率。因此，对三维点云特征进行特征选择以提升后续分类器的准确率是有实际价值的。

1.2 特征选择算法

根据是否使用样本的标签信息，特征选择算法可分为无监督、半监督、有监督3类。由于无标签信息，即无监督方法通常使用数据的相似度、数据重建误差等准则来评估特征的重要程度[12]。半监督方法的动机是使用少量的有标签数据作为无监督方法的补充信息来提升方法的性能，其适用于小样本问题。Fisher算法[13]是一种常见的特征选择算法，可计算全体样本的类内方差和类间偏离程度，将两者的比值作为特征的得分。ReliefF[14]算法根据样本以及邻近样本的相关性来评价特征。量化MI[15]算法利用量化的离散变量计算信息熵，是十分适用于大规模超高维的数据集。ILFS[16]是全部可能的特征子集的得分。TRC[17]优化了特征子集的得分准则。在半监督和无监督方法范畴下，RLSR[18]利用重新调节的回归系数来对特征进行评估；Inf-FS[19]将特征视为全连接图上的节点；LRLMR[20]将潜在的代表行学习嵌入进无监督特征选择；DGUFS[21]基于L2,0范数设计了无映射特征选择模型。然而，上述方法对特征的评估准则均基于数据库中全部样本的表现，而忽略了一些特殊样本对特征评分的影响。为公平起见，本文重点关注有监督特征选择算法。但为了更加全面地验证本文提出的FSSO方法，半监督和无监督特征选择算法也参与了实验比较。

2 本文方法

图2为FSSO算法的总体框架。

图2 FSSO算法的总体框架

2.1 相关符号和定义

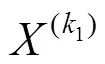
2.2 三维点云优化的类均值中心计算方法

一般特征选择方法基于全部样本计算类均值中心，由于特殊离群样本不能准确地反映类簇的主要特性，使用其得到的均值中心往往会偏向于离群样本聚集的区域，从而影响特征评分(图3)。

图3 常见的均值中心和优化的均值中心比较

本文三维点云类中心计算方法的关键步骤为：

(2) 基于剩余样本计算各类均值中心。根据上述公式和定义，三维点云优化的类中心计算算法为：

算法1.三维点云的类中心计算算法。

输入：各类样本集(k),= 1, 2,···,；各类的样本总数n；参数。

输出：优化的类均值中心(k),=1, 2,···,。

for=1, 2,···,do

显然，由于在计算三维点云类中心时排除了离群者，此优化类均值中心能更加准确地代表类别的特性，且不受离群样本影响。

2.3 三维点云的离群样本和冗余特征

2.4 基于特殊离群样本优化的三维点云特征选择

本文受文献[22]采用方向性离群样本的特征选择算法的启发，提出了基于上述特殊离群样本优化的特征选择算法，并将直接筛除冗余特征的优化操作用于计算各个特征的得分，从而更加精准地实现对特征的选择。即将={1,2,···,}记为初始特征集合。

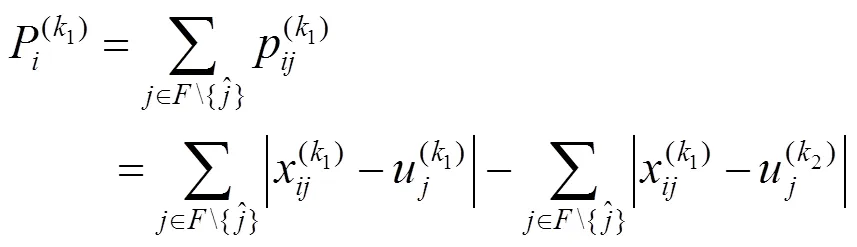
基于上述公式和分析，三维点云特征选择算法为：

算法2:基于SOs的特征选择算法。

输入：参数；选择的特征数。

输出：经选择的特征集合。

初始化={1,2,···,};

do

6. 最终选择得分最高的个特征。

3 实 验

本文实验选择在3个开源的大规模三维点云分类数据集(ModelNet40，IntrA，ShapeNetCore)上进行实验，分别与5种方法进行了比较，并使用评价指标——分类准确率进行评估对比。此外，为论证FSSO的适用性，还在4个高维人工特征数据集(USPS，TOX_171，lymphoma，CLL_SUB_111)上进行了验证。

3.1 数据集

ModelNet40[23]是人造物体点云数据集，包含12 311个物体，涵盖40个类别。遵循官方提供的实验设置，其中9 843个物体用于训练，剩余的2 468个物体用于测试。对该数据集使用CurveNet[9]进行特征提取，取网络分类层的输入作为提取的样本特征，维数为2 048。

IntrA[24]是一个二分类的颅内动脉瘤的3D数据集，包含正常的血管片段和动脉瘤片段共2 025个样本。实验设置遵循五折交叉验证方式。采用3DMedPT[10]对IntrA数据集进行特征提取，取网络分类层的输入作为提取的样本特征，相应特征维数为512。

ShapeNetCore[25]数据集包含51 300个三维模型，覆盖55个类别。依据官方提供的实验设置，该数据集的训练集、验证集和测试集分别含35 708，5 158和10 261个样本，其中验证集仅在训练深度模型时用到，保存验证集上表现最好的模型参数。使用DGCNN[11]对ShapeNetCore数据集进行特征提取，取网络分类层的输入作为提取到的样本特征，相应的维数为512。

这里CurveNet，3DMedPT和DGCNN均作为三维点云样本的特征提取器，提取到的特征直接作为特征选择算法的输入。

此外，为充分地验证FSSO的有效性，还在4个高维/较大规模手工特征数据集上进行了实验：USPS，是手写体数据集，含9 298个样本，涵盖0～9是个类别，特征维数是256；TOX_171，是生物数据集，涵盖4个的共171个样本，特征维数是5 748；lymphoma，是生物基因数据集，有来自 9个类别的96个样本，维数是4 026；CLL_SUB_111是基因数据集，共111个样本，来自3个类别，特征维数是11 340。

3.2 对比方法和实验设置

表1展示了9种对比方法和基准方法(Baseline)的相关信息，其中基准方法指所有原始特征均被选择。，，，分别代表样本数、特征维数、类别数和算法的迭代次数。

表1 本文实验涉及到的对比方法的基本信息

表1还给出各算法的时间复杂度，其数据均来自其参考文献，若未提及，则用符号“-”替代。本文FSSO的时间复杂度包含2个部分，一是优化的类均值中心算法的时间复杂度，需要()的时间；二是基于类内相对偏离的特征选择算法的时间复杂度。该特征选择算法基于特殊离群样本的类内相对偏离，考虑到一个数据库中的离群样本数远小于样本总数，因此特征选择算法需要的时间小于()，那么FSSO的时间复杂度则最多为(+)。对于大多数的三维点云数据集，FSSO方法的时间损耗是可接受的。

本文实验采用2种常见的分类器验证分类效果，即：线性支持向量机(support vector machine，SVM)和K-近邻分类器(K-nearest neighbor algorithm，KNN)。其中，设置KNN分类器的参数为=2,3,···,10，并选取最高分类准确率作为最终的结果。

遵循文献[22,26]的工作，本文对所有方法采用网格搜索法，选择不同百分比下的特征数并计算相应的分类准确率，将其中的全局最优的结果作为实验结果展示。

3.3 实验结果与分析

表2为不同对比方法、不同分类器在三维点云数据集ModelNet40，IntrA和ShapeNetCore上的全局最优分类结果。值得注意的是，由于TRC，DGUFS和LRMLR涉及计算求逆矩阵或成对样本之间的距离，计算成本十分巨大，故不使用LRMLR对样本数超过50 000的大规模数据集ShanpeNetCore进行实验。图4为在ModelNet40，IntrA和ShapeNetCore上，当选择不同百分比特征数时得到的分类准确率，5种进行比较的方法为：ReliefF，MI，ILFS，RLSR和Inf-FS。注意到，由于二分类数据集IntrA的2个类别下的样本数差别巨大，因此，基于SOs筛选特征的FSSO算法会在类内偏离不再减小时自动停止特征选择，故在图4(c)和(d)中，分别选择前65%，70%，···，95%特征数进行比较。显然对于3种数据集，本文的FSSO算法位于其他对比方法的上方，说明FSSO选择出的特征子集表现更好，能获得更高的分类准确率。此外，还可以得到如下结论：

(1) 表2展示的在全部数据集上、无论何种分类器，FSSO算法得到的分类准确率稳定地优于Baseline，这不仅说明对三维点云数据进行特征选择是十分有必要的，并且表明了FSSO算法能有效地选出有识别力的特征子集。反观一些对比方法，如Inf-FS，DGUFS和LRMLR等，其分类表现普遍劣于Baseline；

(2) 相较于其他对比方法，FSSO选出的特征子集表现的更加出色，如，在ModelNet40上，FSSO+SVM (93.03%)比次佳的ReliefF+SVM (92.95%)多正确分类了3个样本；在IntrA上，FSSO+KNN (96.99%)比次佳的ReliefF+KNN (96.94%)多正确分类了1个样本。值得注意的是，对于像IntrA这样的医学影像数据集，正确分类样本数的提高是具有实际应用价值的；

(3) 结合图4可以发现，选择50%～90%特征数时，FSSO比其他对比方法有更加显著地分类优越性。这说明FSSO能够优先筛除冗余特征、更多地保留特征原始信息。

表2中有多个方法在ModelNet40和IntrA上取到了相同的全局最优分类准确率，因此在表3中列出了取得该准确率时对应的特征数。结合表3可以看到，在大多数情况下FSSO在选择较少特征时已可以取得其全局最优结果，这是因为在FSSO特征选择过程中，最冗余的特征总是被最先找到并被赋予较小的得分，这种方式得到的特征评分相较于其他对比方法更加准确。

表2 各方法在ModelNet40，IntrA，ShapeNetCore上的全局最优分类准确率(%)

注：加粗数据为最优值

图4 5种对比方法(ReliefF，MI，ILFS，RLSR和Inf-FS)与FSSO在不同特征数百分比下的分类准确率比较

表3 各方法在取得最优分类准确率时的特征维数百分比(%)

3.4 FSSO在高维手工特征/较大规模数据集上的补充验证

表4给出了本文方法在4个高维/较大规模手工特征数据集上的结果。可见，本文方法比其他特征选择算法的分类准确率更高，说明本文方法在高维和较大规模的手工特征数据集上仍然表现出较好的性能。

表4 在高维/大规模手工特征数据集上的全局最优分类准确率，采用SVM分类器(%)

注：加粗数据为最优值

3.5 参数分析

使用SVM作为分类器对FSSO中的参数和进行分析。由图5可见，FSSO在5个数据集上的准确率均较稳定，而出现下降的情况集中在图的四周，即当或过大或过小时，准确率略有下降。图5结果表明，FSSO对参数不敏感，当参数在一个较大的范围内变化时，FSSO的分类准确率仍能保持稳定。因此，ModelNet40上建议参数区间为Î[0.7,0.9]，Î[3.8,4.2]；IntrA建议为Î[0.7,0.9]，Î[2,2.4]；ShapeNetCore建议为Î[0.7,0.9]，Î[8.2,8.6]；TOX_171建议为Î[0.5,0.7]，Î[2,2.2]；CLL_SUB_111建议为Î[0.9,1]，Î[1.6,1.8]。

图5 不同参数组合下FSSO的比较结果(SVM分类器)

4 总结与展望

针对三维点云特征中包含大量冗余成分的问题，本文提出了一种新的特征选择方法——基于特殊离群样本优化的特征选择算法(FSSO)。首先计算优化的均值中心，接着通过计算特殊离群样本的类内相对偏离程度给特征赋值并进行筛选。与其他特征选择算法相比，本文方法有2个显著优势：①在3个广泛使用的点云分类数据集和4个高维/大规模手工特征数据集上取得了最优或接近最优的准确率，表明了本文方法有效地去除了冗余特征；②在一定范围内调节2个参数，算法仍保持较高的准确率，表明算法对参数不敏感。实验结果表明FSSO选择出的特征能够获得更好地分类效果，且计算效率更高。后续工作将聚焦于设计出更加合理的类中心算法、设计更准确的特殊离群样本捕捉算法，以提升特征选择算法的性能。

[1] 王文曦, 李乐林. 深度学习在点云分类中的研究综述[J]. 计算机工程与应用, 2022, 58(1): 26-40.

WANG W X, LI L L. Review of deep learning in point cloud classification[J]. Computer Engineering and Applications, 2022, 58(1): 26-40 (in Chinese).

[2] DENG S, FENG Y D, WEI M Q, et al. Direction-aware feature-level frequency decomposition for single image deraining[C]//The 13th International Joint Conference on Artificial Intelligence. California: International Joint Conferences on Artificial Intelligence Organization, 2021: 650-656.

[3] 刘艺, 曹建军, 刁兴春, 等. 特征选择稳定性研究综述[J]. 软件学报, 2018, 29(9): 2559-2579.

LIU Y, CAO J J, DIAO X C, et al. Survey on stability of feature selection[J]. Journal of Software, 2018, 29(9): 2559-2579 (in Chinese).

[4] CHARLES R Q, HAO S, MO K C, et al. PointNet: deep learning on point sets for 3D classification and segmentation[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2017: 77-85.

[5] QI C R, YI L, SU H, et al. PointNet++: deep hierarchical feature learning on point sets in a metric space[C]//The 31st International Conference on Neural Information Processing Systems. New York: ACM Press, 2017: 5105-5114.

[6] ZHAO H, JIANG L, FU C, et al. Pointweb: Enhancing local neighborhood features for point cloud processing[C]//IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2019: 5565–5573.

[7] LI J, CHEN B, LEE G. So-net: self-organizing network for point cloud analysis[C]//IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2018: 9397-9406.

[8] XU Q, SUN X, WU C, et al. Grid-gcn for fast and scalable point cloud learning[C]//IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2020: 5661-5670.

[9] XIANG T G, ZHANG C Y, SONG Y, et al. Walk in the cloud: learning curves for point clouds shape analysis[C]//2021 IEEE/CVF International Conference on Computer Vision. New York: IEEE Press, 2021: 895-904.

[10] YU J, ZHANG C, WANG H, et al. 3D medical point transformer: introducing convolution to attention networks for medical point cloud analysis[EB/OL]. [2022-01-04]. https://arxiv.org/abs/2112.04863.

[11] WANG Y, SUN Y, LIU Z, et al. Dynamic graph CNN for learning on point clouds[J]. Acm Transactions on Graphics, 2019, 38(5): 1-12.

[12] LI J D, TANG J L, LIU H. Reconstruction-based unsupervised feature selection: an embedded approach[C]//The 26th International Joint Conference on Artificial Intelligence. New York: ACM Press, 2017: 2159-2165.

[13] DUDA R O, HART P E, STORK D G. Pattern classification[M]. 2nd Edition. Boston: McGraw-Hill, 2001: 177-179.

[14] KONONENKO I. Estimating attributes: analysis and extensions of RELIEF[J]. European Conference on Machine Learning, 1994, 784: 171-182.

[15] ZHANG Y, WU J, CAI J. Compact representation of high-dimensional feature vectors for large-scale image recognition and retrieval[J]. IEEE Transactions on Image Processing, 2016, 25(5): 2407-2419.

[16] ROFFO G, MELZI S, CASTELLANI U, et al. Infinite latent feature selection: a probabilistic latent graph-based ranking approach[C]//2017 IEEE International Conference on Computer Vision. New York: IEEE Press, 2017: 1407-1415.

[17] NIE F, XIANG S, JIA Y, et al. Trace ratio criterion for feature selection[C]//The 23th AAAI. Palo Alto: AAAI, 2008: 671-676.

[18] CHEN X J, NIE F P, YUAN G W, et al. Semi-supervised feature selection via rescaled linear regression[C]//The 26th International Joint Conference on Artificial Intelligence. New York: ACM Press, 2017: 1525-1531.

[19] ROFFO G, MELZI S, CRISTANI M. Infinite feature selection[C]//2015 IEEE International Conference on Computer Vision. New York: IEEE Press, 2015: 4202-4210.

[20] TANG C, BIAN M, LIU X, et al. Unsupervised feature selection via latent representation learning and manifold regularization[J]. Neural Netw, 2019, 117: 163-178.

[21] GUO J, ZHU W W. Dependence guided unsupervised feature selection[EB/OL]. [2021-12-13]. https://zhuanlan.zhihu.com/p/ 37216951.

[22] YUAN L, YANG G, XU Q, et al. Discriminative feature selection with directional outliers correcting for data classification[J]. Pattern Recognition, 2022, 126: 108541.

[23] WU Z R, SONG S R, KHOSLA A, et al. 3D ShapeNets: a deep representation for volumetric shapes[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2015: 1912-1920.

[24] YANG X, XIA D, KIN T, et al. Intra: 3d intracranial aneurysm dataset for deep learning[C]//IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2020: 2656-2666.

[25] CHANG A, FUNKHOUSER T, GUIBAS L. Shapenet: an information-rich 3D model repository[EB/OL]. [2022-01-06]. https://arxiv.org/pdf/1512.03012.pdf.

[26] NIE F P, YANG S, ZHANG R, et al. A general framework for auto-weighted feature selection via global redundancy minimization[J]. IEEE Transactions on Image Processing, 2019, 28(5): 2428-2438.

A new 3D point clouds feature selection method using specific outliers optimization

HUANG Xiang, WANG Hong-xing, GU Xu, MENG Yue, WANG Hao-yu

(Jiangsu Frontier Electric Power Technology Co., Ltd., Nanjing Jiangsu 211102, China)

With the rapid development of technologies in metaverse, digital twins, virtual and augmented reality, three-dimensional (3D) point clouds have been widely applied to electric power, construction, advanced manufacturing, and other industries. As a result, how to reduce the redundancies of 3D point clouds data and how to effectively select useful point cloud features have played a critical role in the full use of massive point clouds data. Considering that most of the current feature selection methods pay little attention to specific instances, in this paper, we proposed a novel supervised feature selection method, named feature selection based on specific outliers optimization (FSSO). Specifically, in order to obtain accurate specific outliers (SOs), we first optimized the traditional mean center of class, and automatically defined the class majority. Then, we proposed the feature selection algorithm that could compute the intra-class relative deviation of SOs, and score features based on the deviations. Extensive experiments on 3D data clouds classification datasets (ModelNet40, IntrA, and ShapeNetCore), and on four high-dimensional handcrafted datasets show that the proposed FSSO can select discriminative features, and improve the classification accuracy.

three-dimensional point clouds; supervised feature selection; specific outliers; intra-class relative deviation degree; classification

TP 391

10.11996/JG.j.2095-302X.2022050884

A

2095-302X(2022)05-0884-08

2022-04-02；

2022-06-22

2 April，2022；

22 June，2022

黄 祥(1990-)，男，工程师，本科。主要研究方向为高压电气试验、无人机电力巡检作业及电力巡检图像识别等。E-mail：huangxiang1124@sohu.com

HUANG Xiang (1990-), engineer, bachelor. His main research interests cover include high-voltage electrical test, UAV power patrol operation and power patrol image recognition. E-mail：huangxiang1124@sohu.com