三角形外心创设，创新题向量应用

胡景月

(南京市雨花台中学，江苏南京，210000)

与三角形的“心”有关的问题，是巧妙融合初中与高中知识的一类综合应用问题，也是很多同学处理起来比较困难的一类问题．而三角形的外心经常与平面向量加以交汇，巧妙融合了平面几何中的三角形与圆这两个基本图形，同时隐含着对应的垂直关系，以平面向量的数量积的不同形式来创设，情境创新，应用性强，是平面向量与解三角形问题中比较热点的一类题型，倍受各方关注．

1 数量积的值

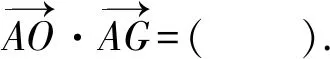
A． 16 B. 8 C. 24 D. 32

分析：根据题目条件，通过平面几何图形的直观形象，结合平面向量的线性运算，通过平面向量的数量积公式加以展开，合理分解与转化，并利用投影的几何意义加以转化与应用，进而得以确定对应平面向量的数量积的值．

图1

解析：如图所示，取AB的中点D，联结OD，依题意可得OD⊥AB，

故选择答案：D．

点评：借助三角形外心的几何特征与结构性质，利用平面几何中辅助线的构建确定对应边之间的垂直关系，从而为进一步利用平面向量的数量积公式转化提供依据，方便数量积公式的化简与运算，特别是投影的几何意义的应用以及两垂直平面向量的数量积为零等性质，为解决平面向量的数量积的值指明方向．

2 数量积的最值

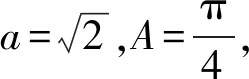
A． 0 B. 1 C. 3 D. 5

分析：根据题目条件，通过正弦定理确定三角形的外接圆的半径，由此确定三角形边的取值范围，通过数形结合，结合三角形外心的性质，利用平面向量中投影的几何意义以及余弦定理的平面向量公式分别确定对应的关系式，进而确定所求数量积的表达式，利用二次函数的图象与性质来确定最值问题．

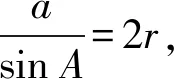
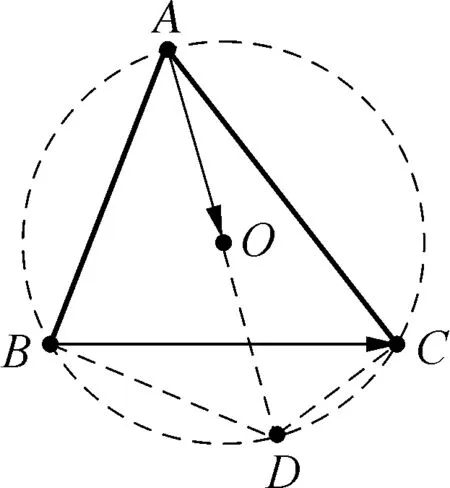
图2

结合三角形的外接圆的几何性质，则有b∈(0，2]，

如图所示，延长AO交外接圆O于点D，连接BD，CD，

由于AD是外接圆O的直径，则有AB⊥BD，AC⊥CD，

点评：抓住三角形外心的几何性质，从“数”的视角内涵上确定三角形边长的取值范围，又从“形”的视角实质上确定平面几何中的垂直关系，两者综合应用，进一步将平面向量中投影的几何意义、余弦定理的平面向量公式等加以融合，有“数”的内涵，有“形”的特征，创新新颖．

3 代数式的值

分析：根据题目条件，利用平面向量的线性关系，通过平面向量数量积公式，结合三角形外心的性质，利用平面向量中投影的几何意义，从两个不同层面构建对应的数量积关系式，进而确定两个不同的线性关系式，结合线性规划问题来分析与处理，进而确定对应的代数式的取值问题．

解析：如图所示，连接OB，OC，

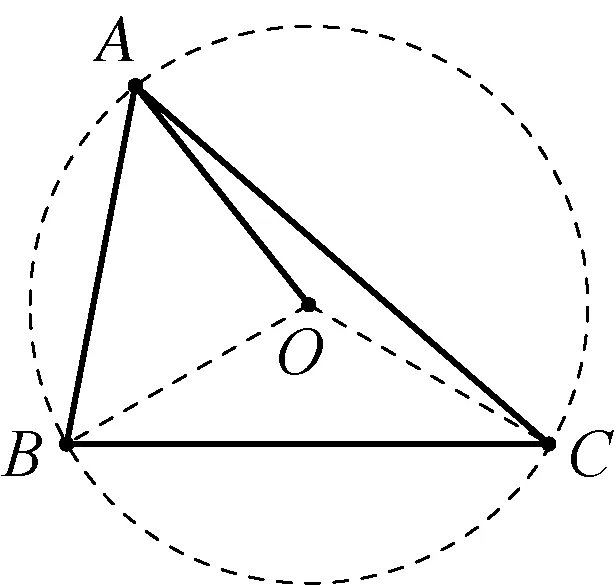
图3

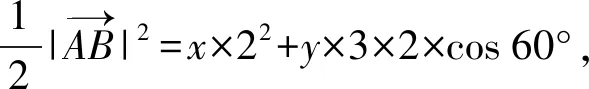
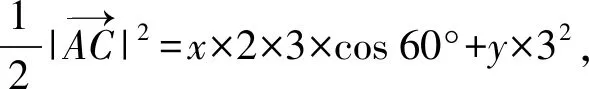
点评：解决问题的关键就是从题中平面向量的线性关系的“数”的性质，综合三角形外心的“形”的特征，数形结合，利用三角形的外心的性质以及投影的几何意义加以应用，合理构建满足条件的关系式，为进一步代数式的求值提供条件．“数”与“形”的合理融合与巧妙过渡，共同实现问题的解决与应用．

4 综合问题

例4(多选题)已知点O是△ABC的外心，则( ).

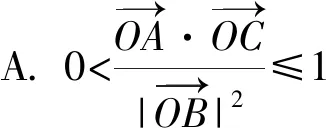
分析：根据题目条件，以点O是△ABC的外心，结合各选项中不同的条件，借助平面向量的线性运算、数量积公式、投影的几何意义以及平面向量的夹角公式等加以转化与运算，从而实现命题真假的判定．

对于选项B，设AB中点为M，则OM⊥AB，如图所示，

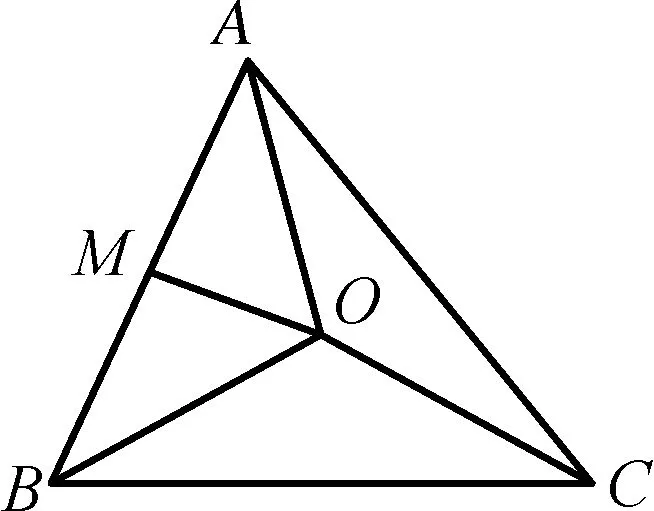
图4

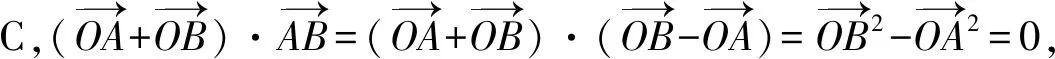
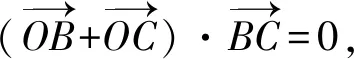
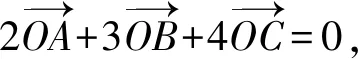
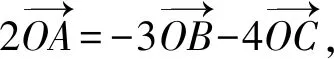
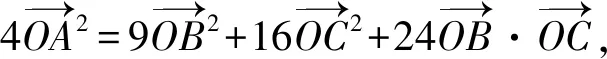
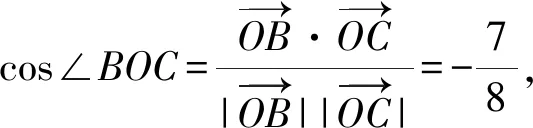
故选择答案：BCD．

点评：借助三角形外心的问题背景，可以交汇与融合平面向量的线性运算、数量积公式、投影的几何意义以及平面向量的夹角公式等众多的平面向量知识，结合多选题、命题真假判定等形式来设置，实现综合问题的展示与应用．此类综合应用问题，可以渗透更多的知识点、数学能力等，充分考查逻辑推理、直观想象、数学运算等核心素养．

根据不同场景下三角形外心问题的巧妙创设，合理将平面向量与解三角形中的相关知识加以合理交汇与融合，以平面向量的数量积的不同形式与场景出现，进而解决形式多样的数学问题，巧妙挖掘题目条件的内涵与实质，实现基础知识、基本能力的综合与应用，加强初中与高中相关数学之间的联系与应用．