数形结合思想在小学数学计算教学中的应用

■山东省枣庄市台儿庄古城学校 刘汉民

数形结合思想是数学教学中十分重要的思想形式，可以通过数与形之间的结合来帮助学生进行数学知识的理解，也可以帮助学生进行解题，有效促进小学生数学素养的同步提升。学生的计算能力培养十分关键，教师可以利用数形结合思想来进行计算教学过程中的渗透，从而实现学生计算能力的提升。那么如何才能在数学计算教学中进行数形结合思想的应用呢？笔者对此进行了探究和分析。

一、数形结合思想概述

数形结合思想是数学学习中十分重要的一种思想方式，主要是能更好地将数字和图形进行一定的结合，从而能有效帮助学生来进行数学知识的学习和数学问题的解答。数形结合思想进行互相转化，能将数字转化为图形，也可以将图形转化为数字。有时候数字和图形之间是对应关系，不同的数学题中，可以进行数字的表示，也可以进行图形的表示，可以根据具体的内容来帮助学生进行数学题意的理解，也能帮助学生找到具体的解题思路，促进学生数学计算能力的提升。

二、数形结合思想的重要性

数形结合思想对小学生的数学计算学习来讲具有十分重要的作用，一方面，能培养学生的数形结合思想，让其能在小学生的大脑中形成一定的概念，在日后的数学学习中发挥作用。数形结合是一种非常常见的思想，无论是小学数学的学习，还是后来的初中、高中数学，都会进行数形结合思想的应用，教师可以在小学初级阶段的数学教学中进行数形结合思想的渗透，对学生日后数学成绩和学科素养的提升起到非常重要的作用。另一方面，还能帮助学生进行计算题的解题工作，很多计算题有一点难度，对小学生而言，他们的数学学习基础比较薄弱，解题的数量比较少。因此，在解题中会遇到一定的困难。而利用数形结合思想能更好地帮助学生进行解题，有效促进学生的数学理解，提升学生数学解题水平。

三、数形结合思想的使用原则

（一）科学性原则

教师在进行数形结合思想的运用时，应该遵循一定的使用原则，这样才能让课堂教学具有更好的效果。教师应该运用科学性原则来进行数形结合思想的渗透，数形结合思想虽然具有非常重要的作用，但是不是所有的计算教学都能进行应用。教师应该具体问题具体分析，不能为了应用而应用，这样会造成形式化主义严重的问题出现，不但不利于学生的数学成绩提升，而且会浪费数学课堂的教学时间。

（二）主体性原则

教师在小学数学计算教学中应该采用主体性的原则来进行数形结合思想的融入，教师应该明白学生才是计算学习的主体。那么就应该在教学设计中对学生的学习情况进行考虑，这样才能进行数形结合思想的应用，让其应用质量变得更高，促进学生学习成绩的提升。教师还应该让学生充分参与到数形结合思想的使用中，只有这样才能让学生对此种数学思想更了解。通过主动参与，学生在日后的自主学习中适当地进行数形结合思想的运用，从而促进学生的计算水平提升。

（三）实践性原则

教师在进行计算教学时，应该采用实践性的原则来进行数形结合思想的渗透。数形结合思想的学习不仅要进行理论方面知识的了解，更要通过不断实践练习才能为学生打牢基础，从根本上进行概念的理解和运用。教师可以通过具体的例题分析来进行教学讲解，有效促进学生的对数形结合思想的掌握，帮助学生实现自身数学计算能力的提升。教师可以利用课堂时间进行计算作业的例题分析，让学生能不断进行数形结合思想的应用练习，这样才能实现对学生的学习帮助，发挥数形结合思想的有效作用。

四、数形结合思想在小学数学计算教学中的运用

（一）通过数形结合理清数量关系

教师在进行计算教学的过程中，要让学生进行数量之间关系的厘清，这样才能让学生对整个计算题目更加了解，对学生的解题工作具有非常清晰的思路。因为很多数学计算题都是通过汉字的形式来进行阐述，这样会让学生在理解方面具有一定的困难，只有通过图形的形式来进行展示，才能给学生更直观的感受，促进学生进行数量之间关系的梳理。教师就可以在进行计算教学中进行数形结合思想的使用，帮助学生厘清各个数量之间的关系，提升学生的感悟能力。

比如，在解这道题时：某仓库中存储了一定数量的水泥，第一天运走了整个仓库水泥数量的第二天又运来了22吨水泥。此时，仓库中的水泥数量比最开始多了那么请问原来仓库里一共存储了多少吨水泥？

一般学生在进行计算工作前，都要进行题目的阅读和理解，但是很多学生阅读之后都存在着一定的理解性困难。题目中的各个数量关系到底是如何呢？会在学生的大脑中产生非常多的疑问。学生之所以会产生各种疑问，是因为题目中的数量关系比较复杂，而且其中出现的分数之间可能会有一些重叠的关系，这样会让学生的大脑出现混乱，不利于最终的解题。那么教师就可以通过数形结合的思想来进行计算教学，让学生能厘清题目中各个数量之间的关系，这样才能帮助学生进行解题。题目中各个数量之间的关系如图1所示：

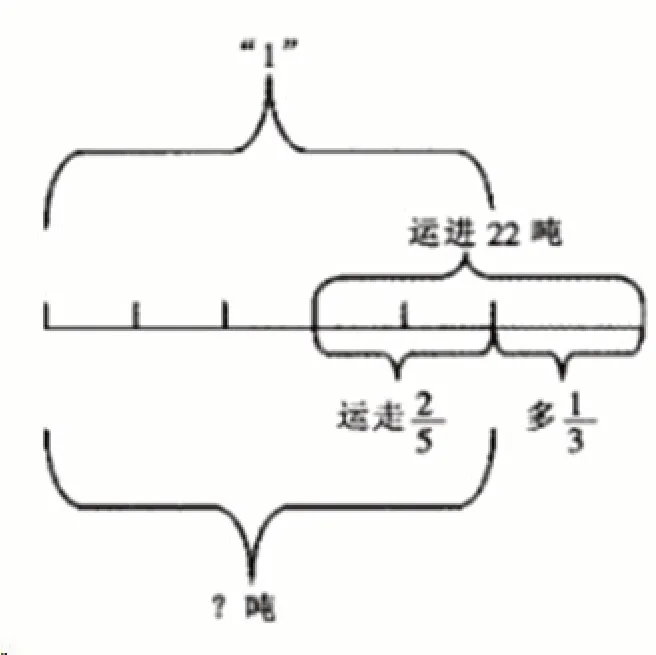
图1 水泥存储数量关系

教师在进行图片的展示后，可以通过数形结合的思想来进行例题的讲解，这样能更好地帮助学生进行数形结合思想的学习，也能促进学生数学计算能力的提升。为了能让学生成为数学计算教学中的主体，教师可以通过一定的互动形式来进行课堂教学实施。例如，教师可以问学生，从图形中能看到什么样的数量关系呢？可以通过学生的举手来进行回答，也可以教师随机进行提问。当学生课堂回答结束后，教师可以进行具体的例题讲解。通过这样的课堂互动教学，不但有助于学生的课堂思考和主动探究，还能实现学生对数形结合思想的领悟。从图中能看到原来的水泥整体数量被看作是1，后来运走了，之后又运来了22吨水泥，不仅将原来运走的进行填充，还多出了原来水泥数量的，那么我们就能在其中找到一定的等量关系，那么就是原来水泥量的的和也就是22 吨，这样就能算出来原来的水泥量。教师已经为学生进行解题思路的查找，学生要通过这个等量关系进行计算，最后求出结果。教师通过数形结合的方式来进行例题的讲解，会给学生提供更加直观的数量关系，从而能帮助学生完成计算工作。此题虽然是计算类的应用题，但是其中的关键是要厘清各个数量之间的关系，利用数形结合思想可以更好地进行解题，有助于促进学生解题能力的提升。

（二）通过数形结合提高理解能力

在进行数学计算工作中，很多学生因为缺乏一定的抽象思维能力，这样会造成对计算题无法进行深入理解，这样不利于学生的计算题解答。那么教师就可以进行数形结合思想的运用，帮助学生理解计算题的内在原理，这样才能让学生真正地实现对数学计算的理解，促进学生计算水平的提升。

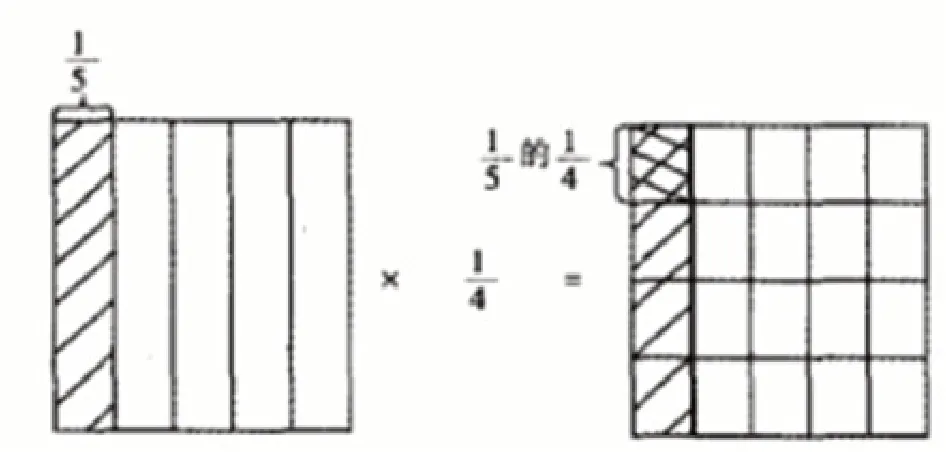
图2 分数乘法计算

从图中能看到，教师将一个正方形平均分成了5份，取其中的一份来用斜线标记，证明该区域是整个图形中的然后教师又将的区域平均分成4份，并且将其中的一份用斜线进行标记。那么重叠的部分就是二者之积。通过数形结合的方法能让学生明白分数乘法的内在含义，就是将一个整体中的一个部分再看成整体，然后再平分取出其中对应的分数，这样就实现分数乘法的计算。教师可以让学生通过数格子的方式来求出最后的结果为就是将整个大格子平均分成了20份，而最后的结果就是其中的一份。通过数格子解出的最后结果能看出，分数相乘就是分母相乘和分子相乘，最后得到结果。通过教师最后的总结也能告诉学生快速的分数乘法计算方法，提高学生的计算效率。

（三）通过数形结合培养空间观念

很多学生在日常的数学学习中对平面图形具有非常多的了解，但是对三维立体图形的计算却存在一定的问题。之所以会出现这样的情况，就是因为学生不具备三维空间的观念，对学生来讲十分抽象，从而无法完成数学计算工作。那么教师就应该利用数形结合思想来进行学生空间观念的建立，让学生在大脑中能形成三维图形，这样才能帮助学生进行数学计算的思考，有助于帮助提升学生的数学计算能力。比如，在解这道题时：已知一个长方体的长度为5 厘米，宽度为4 厘米，高度为3 厘米。那么请问长方体的占地面积是多少平方厘米？长方体的表面积是多少平方厘米？

因为很多学生无法理解长方体是三维空间图形，在他们的心里只有长方形这样的概念。为了能帮助学生建立三维立体图形的概念，教师可以利用数形结合的方式来进行教学讲解。教师可以通过多媒体大屏幕来进行长方体的图形展示，为了使学生对三维空间的明晰，在图形中运用不同的颜色而进行长、宽、高的标注，如图3所示：

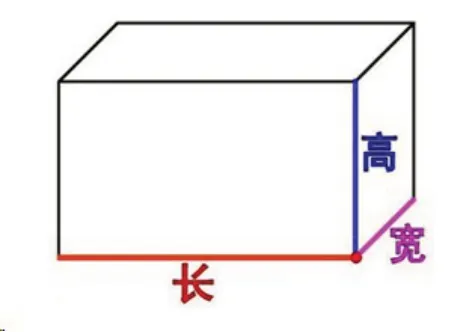
图3 长方体表面积计算

通过图形能看到，长方体的长为红色标注，长方体的宽为紫色标注，长方体的高为蓝色标注。这样标注能让学生建立起初步的三维空间概念，为了能更形象地帮助学生进行三维空间的理解，可以将长、宽、高的交点看作是教室的一个角落，教室的长度、宽度和高度就分别代表了长方体的长、宽、高。通过这样的方式能让学生更直观地进行三维立体图形的观察，也能在大脑中想象到三维图形的样子，有助于学生的计算工作。通过读题，能对长方体的长度、宽度和高度进行全面了解。而题目中第一个问题是问长方体的占地面积是多少平方厘米，占地面积主要是长方体底部所占据的大小决定，那么就是长方体的底部面积，也就是用长度乘以宽度为5×4=20平方厘米。第一个计算问题已经解决，那么第二个问题是要求长方体的表面积，表面积就是所有面的面积之和。教师可以让学生通过图形来观察长方体一共有多少个面，通过观看发现一共有6 个面，分别是2 个长乘以宽，2 个长乘以高和两个宽乘以高，那么就能算出长方体的表面积为5×4×2+5×3×2+4×3×2=40+30+24=94平方厘米。总之，教师通过数形结合的方法能促进学生进行小学数学计算题的解答，可以帮助学生建立三维立体空间的概念，有助于学生的解题。

综上所述，小学生的数形结合思想培养十分重要，不仅能促进学生进行数学学习能力的提升，还能在数学计算教学中发挥十分有效的效果。对小学生而言，只有学生对题目进行深入了解，才能为后续的解题工作带来更多的思路，促进小学生计算能力的提升。