具有时滞的Lotka-Volterra食饵-捕食者成年种群模型的稳定性分析

杨巧艳,廖代琴,颜向平

(兰州交通大学数理学院,甘肃 兰州 730070)

1.引言

随着生物科学的迅速发展,越来越多的研究者逐渐意识到时滞对种群生物学的巨大影响,在种群的进化中,时滞是不可避免的.在现实世界里,任何生物种群都处于某一群落中,且与别的种群发生着一定的联系,因此,在不同的种群之间既存在着相互依存,又有相互制约.捕食模型的动力学关系是生物数学研究的重要课题之一,至今已有很多学者根据两个物种间的相互作用关系及物种自身的特征建立模型,并对模型的动力学进行了研究.[1-6]考虑到年龄结构与环境等因素的影响,越来越多的研究开始讨论具有时滞的生物模型.如Gopalsamy[7]研究了两种群具有时滞的竞争系统,并建立了共存平衡点的全局稳定性结果.文[8]研究了具有交叉扩散和Holling-II型功能反应的Lotka-Volterra食饵-捕食者模型,讨论了在交叉扩散和Holling-II型功能反应联合作用下是否存在正解.Alomari和Gourley[9]通过考虑两成年种群间的相互竞争作用,提出了下面具有时滞的Lotka-Volterra竞争模型

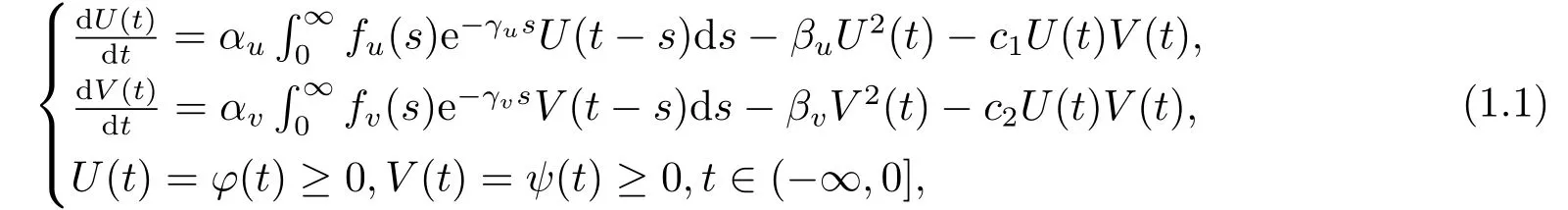
其中U和V分别表示两竞争种群的成年种群密度;正的常数αu和αv分别表示两成年种群的出生率;γu,γv ＞0表示种群在成熟过程中的死亡率;βu,βv ＞0 表示成熟种群的死亡率;c1和c2分别表示两成年种群间的竞争效应.

利用上下解方法和单调迭代原理,Alomari和Gourley[9]分析了系统(1.1)平衡点的全局渐近稳定性,获得了当系统(1.1)的一个边界平衡点线性稳定的而另一个不稳定时,线性稳定的平衡点同时也是全局渐近稳定的;当系统(1.1)的两个边界平衡点都不稳定时,系统(1.1)的共存平衡点是全局渐近稳定的.

在自然界中,种群间的相互作用除了竞争关系外,食饵-捕食者关系也是一种非常重要的种群关系.基于此,本文主要考虑具有时滞的Lotka-Volterra食饵-捕食者模型

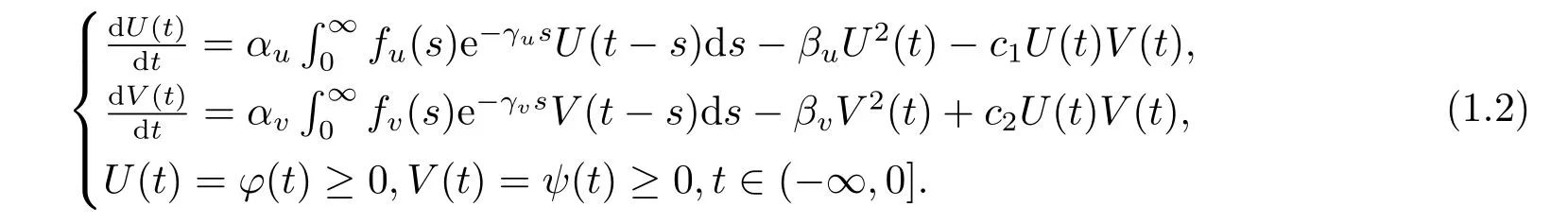
本文首先利用线性化方法和分析特征根在复平面上的分布情况,获得了系统(1.2)边界平衡点的局部渐近稳定性,然后利用比较原理和上下解方法证明了系统(1.2)半平凡平衡点和共存平衡点的全局渐近稳定性.

2.边界平衡点的局部渐近稳定性

容易看到系统(1.2)总是有可行平衡点

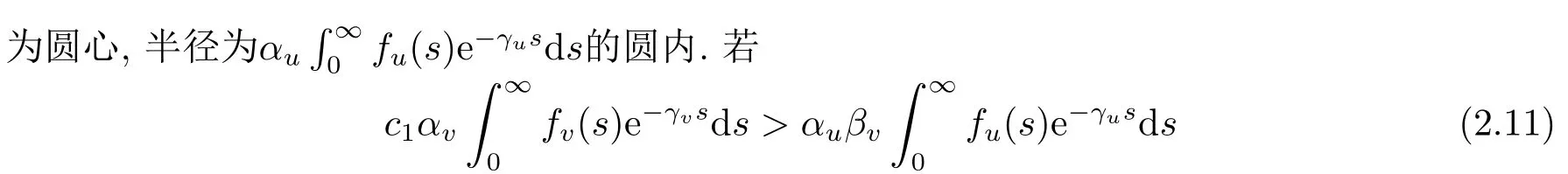
成立,则方程(2.10)的所有根λ具有负实部.因此,当条件(2.11)成立时,系统(1.2)的平衡点是线性稳定的.

3.平衡点的全局渐近稳定性