基于分布式大数据的Expectile回归分析
胡爱军 ,李楚进
(1.湖北第二师范学院数学与经济学院,湖北 武汉 430205;2.华中科技大学数学与统计学院,湖北 武汉 430074)
1.引言
现代技术的发展使得数据采集的规模前所未有,大规模数据集无法在单台服务器上存储,必须分布在具备有限内存的多台机器上,因此通常的经典统计方法不再适用,许多估计和推理方法需要重新研究.在多台机器之间进行数据分块以及并行计算[1]是缓解此类瓶颈的常用方法.
随机抽样和随机投影算法[2-3]已被应用于解决大规模数据的分位数回归问题.但是,在该类算法中,执行子采样需要主内存中有足够大存储空间来存储整个数据集.而且,估计过程中只使用了数据集中的部分数据,而忽略整个数据集来执行估计过程.因此,随机抽样和随机投影算法效果并不理想,并且所得估计效率较低.为了解决这些问题,FAN和CHENG[4],FAN等[5],LI等[6]提出了分块平均估计方法,这种方法显著地解决了存储内存和估计效率两个问题.同样,ZHANG等[7],CHEN和XIE[8]提出了一种分而治之(divide-and-conquer,DC)的方法.它已成功用于解决海量数据集上的均值回归问题,可以大大缩短计算时间并减少存储内存需求.
上述关于DC的研究主要集中在最小二乘线性回归上,而普通最小二乘线性回归对负残差和正残差赋予相同的权重,并将响应变量的期望值估计为协变量的线性函数.基于不对称l1范数的分位数回归,对残差的正负部分赋予不同的权重来改进最小二乘线性回归模型[9-11].与分位数回归模型不同,Newey和Powell[9]基于l2范数提出了以下非对称二次损失函数
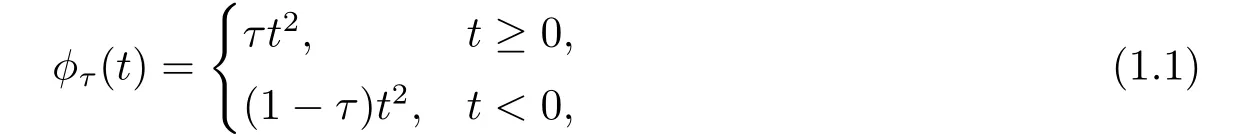
这里τ∈(0,1).随机变量ξ的τ-expectile定义为μτ=自从Newey和Powell[9]提出该模型以来,对expectile回归(ER)统计推断进行了大量广泛的研究[10-12].但是这些方法只能用于中等样本数据的计算.
相对于分位数回归而言,非对称最小二乘法有独特的优点,首先它充分考虑数据的距离和位置信息,期望值比分位数的统计推断更有效,而经验分位数仅利用关于观测值是低于还是高于预测值的信息[13].此外,与样本分位数不同,样本expectile值提供了一类作为水平τ的平滑曲线函数,并且对重尾分布数据表现出更强的鲁棒性[14-15].
然而上述提到的大数据回归建模方法大多是针对均值回归和分位数回归问题的,而对于ER问题的研究很少,尤其是对于大规模数据的ER问题.在本文中,我们提出了分块平均ER(BAER)方法在海量数据集上进行有效的ER估计.该方法包含三个具体步骤: 1)按块顺序分区、存储和读取具有可管理的样本大小的数据集,该数据集可以完全存储在主内存中;2)分别计算每个块内的ER估计量;3)将从每个块获得的估计量的平均值聚合为最终估计量.所提出的BAER方法在海量数据下可以显著地降低对计算机存储硬件的要求,并且得到的估计与将整个数据集集中一起分析的结果一样有效.此外,我们研究了所得估计量的渐近正态性.
2.分布式expectile回归
设随机样本{(xi,yi),i=1,···,N}来自于如下ER模型:

这里xi和yi分别表示p维预测变量和响应变量,εi的τ-expectileφτ(εi)=0.
ER未知参数的估计量可以通过最小化以下非对称最小二乘损失函数得到,

由于上述估计没有显示表达式,通常只能采用迭代的方法计算,然而迭代对于相对较小的数据量是可行的,但是对于海量数据变得越来越困难,当(2.2)中当样本量N过大时,计算空间和时间被确定为潜在的瓶颈.我们的工作建立在FAN等[5],ZHANG等[7],CHEN和XIE[8]等人的方法之上.将观察数据分布式存储在多台机器中.然后我们对每台机器中的数据应用标准ER,并通过简单的平均值组合这些回归结果.我们将此过程命名为BAER方法,它将DC的思想扩展到ER框架.
不失一般性,我们首先将整个数据集随机存储在K台机器中,为简单每台机器数据量为n,即N=nK.记y=(y1,y2,···,yK)T,x=(x1,x2,···,xK)T,这里yk=(y1k,···,ynk)T∈Rn,xk=(x1k,···,xnk)T∈Rn×p,k=1,···,K.
3.算法



迭代BADM算法,直到满足某个停止标准.我们采用Boyd等[16]的停止准则:
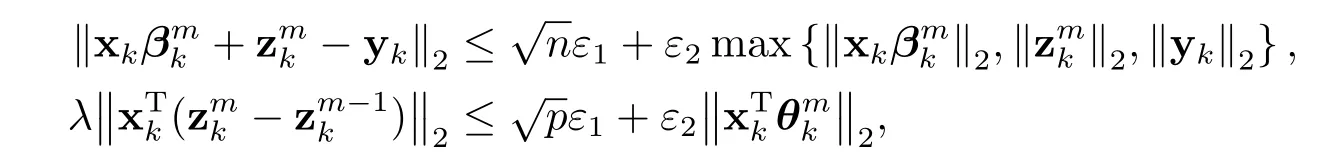
这里通常选择ε1=ε2=10-3,或者当迭代次数超过一定数量如105.
4.渐近性质


5.模拟研究
本节通过模拟研究所提出方法的有限样本性质.比较我们的方法(BAER)与将全部数据集中存储在一台机器内分析的理想方法(Oracle)的表现.
我们考虑数据模型:yik=+σεik,这里φτ(εik)=0,τ∈(0,1),k=1,···,K,i=1,···,n,β0∈Rp,p=20,N=105是总样本量,分布式存储在K=10,100,500台机器中,因此,n=N/K是每台机器上局部样本量.p维协变量xik~Np(0,Σ),Σ=(Σjl)p×p,这里Σjl=0.5|j-l|.真实回归系数β0的每个分量独立并来自U(-3,3).我们考虑三种不同的误差分布:εik~N(0,1),εik~t(3),εik~χ2(2).取σ=1,1+|xik2|分别产生同方差和异方差的数据,这里xik2是xik的第2个分量.我们选择三种不同水平τ=0.3,0.5,0.7,计算估计误差来比较两种方法的表现,独立重复模拟100次.图5.1和图5.2分别给出了同方差和异方差情形下两种方法估计误差的箱线图.表5.1给出了两种方法的计算时间.
根据图5.1和图5.2可以看出,BAER方法估计的结果都与Oracle方法很接近,尤其是机器数K取10和100时,在K=500时估计误差略微增大,这主要是由于此时每块的数据量n=200相对较小.根据表5.1从模拟计算的时间来看,Oracle方法对于大规模数据在实际中通常不可行或者计算耗时较长,而BAER方法即使是在计算最慢的情形下,其计算时间都要比Oracle方法要少,BAER方法在能保证得到较高的估计精度下既提高了计算效率且不受存储内存的限制,这显示出我们的方法在处理大规模数据分析的优良表现.
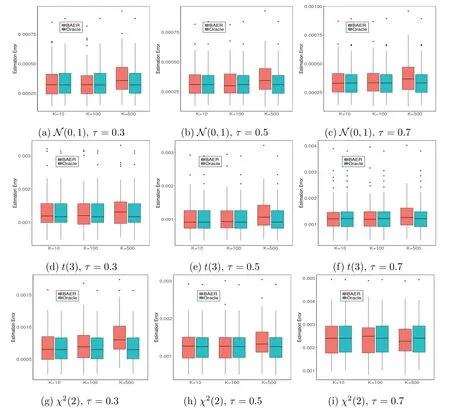
图5.1 两种方法应用于K=10,100,500的同方差模拟数据下的估计误差的箱线图
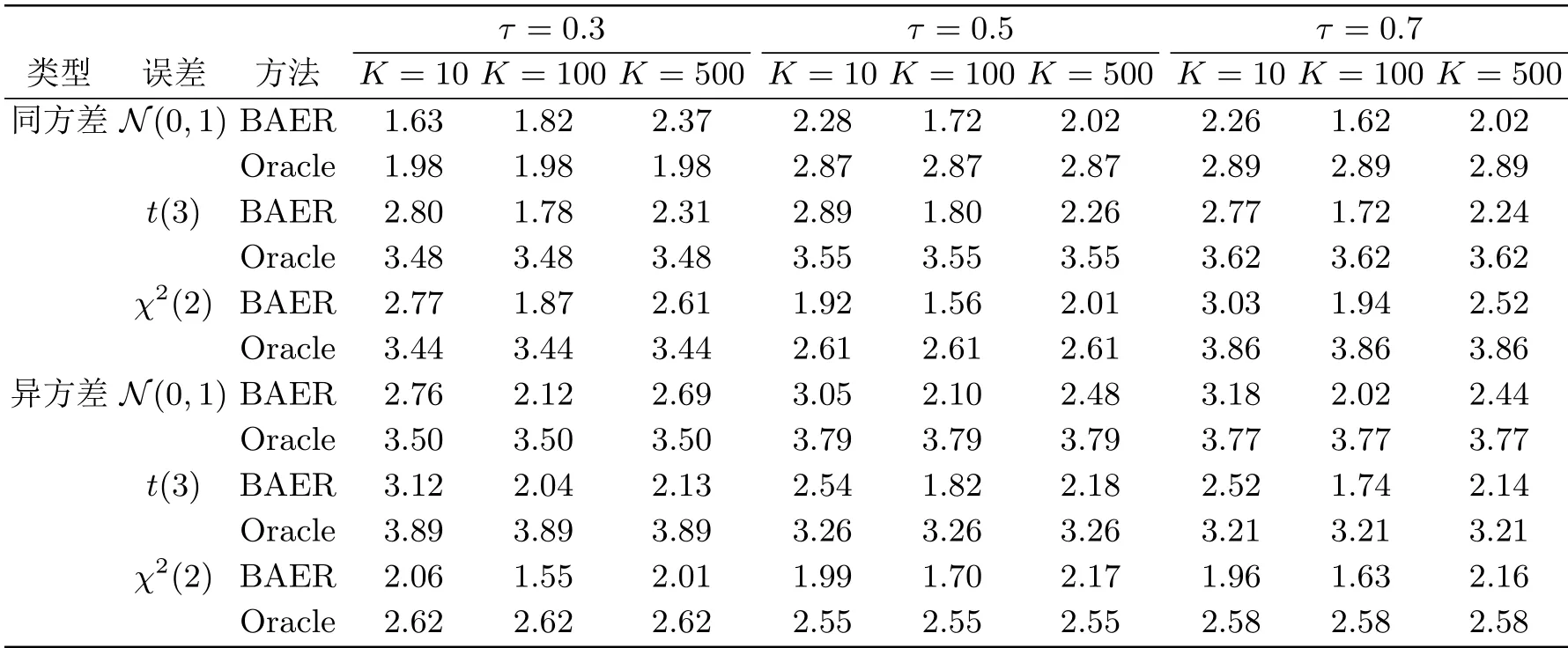
表5.1 两种方法应用于K=10,100,500的同方差与异方差模拟数据下的计算时间(单位: 秒)
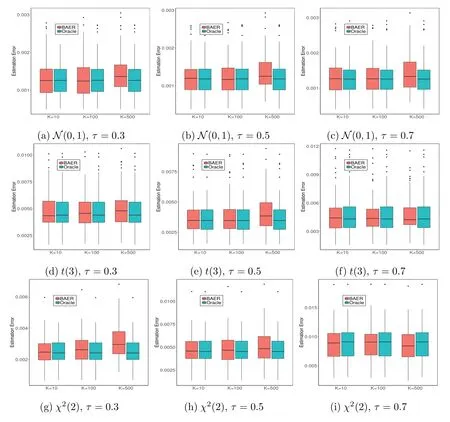
图5.2 两种方法应用于K=10,100,500的异方差模拟数据下的估计误差的箱线图
6.真实数据分析
为了说明我们提出的方法的有效性,我们选取大规模真实数据集进行了分析,以比较上述两种方法的性能.该数据集来自UCI Machine Learning Repository.1http://archive.ics.uci.edu/ml/datasets/Gas+Turbine+CO+and+NOx+Emission+Data+Set该数据集包含来自位于土耳其西北部地区的燃气轮机在一小时内(通过平均值或总和)汇总的11个传感器测量值的36733个实例,用于研究烟气排放,即CO和NOx(NO+NO2).
我们使用其中的10个环境变量: 环境温度(AT),环境压力(AP),环境湿度(AH),空气过滤器压差(AFDP),燃气轮机排气压力(GTEP),涡轮入口温度(TIT),涡轮后温度(TAT),压缩机排气压力(CDP),涡轮发电量(TEY),氮氧化物(NOx)作为预报变量,以空气中一氧化碳(CO)含量作为响应变量建立expectile回归模型.
我们选择τ=0.3,0.5,0.7三种水平下使用交叉验证法来比较上述两种方法的表现.通过对样本随机划分100次,每次随机选取30000个样本作为训练集Dtrain,将剩下的6733个样本作为测试集Dtest.我们将N=30000个训练样本随机地分别存储在K=10,100,300台机器中,相应地每台机器样本量n=3000,300,100.按照WANG等[18],定义预测误差(1/6733)).预测误差的结果在下图6.1中.
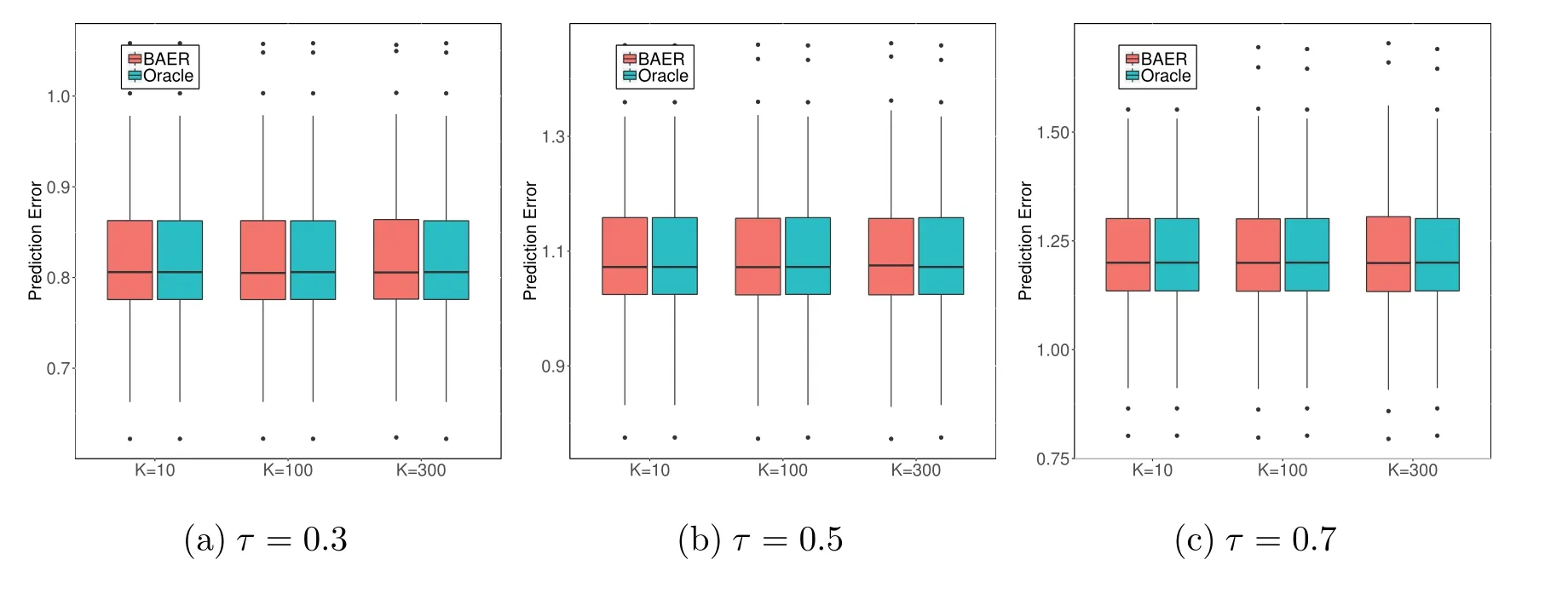
图6.1 两种方法应用于K=10,100,300的燃气轮机排放数据集下预测误差的箱线图

表6.1 两种方法应用于K=10,100,300的燃气轮机排放数据集的计算时间(单位: 秒)
从图6.1中我们可以看出,我们的方法BAER对于三种水平以及三种分块机器数下,都呈现出优良的结果,其预测误差都与Oracle方法非常接近,几乎是没有区别.从表6.1中可以看到,两种方法计算时间基本没区别,当K=300时,BAER方法只比Oracle方法计算时间多0.1秒,这主要由于总体数据量不太大且数据集维数较小,此时分割数据的机器数不宜太大.

