固定效应变系数空间自回归面板数据模型的空间效应检验

翟树芬,苏宇楠,魏传华

(中央民族大学理学院统计学系,北京 100081)

1.介绍

近年来,空间面板数据模型作为空间截面数据和普通面板数据的推广受到越来越多的关注,在理论上得到了深入研究,并被广泛的应用到区域经济学,劳动经济学,房地产经济学等各领域实际问题中.[1-3]

空间面板数据模型从个体效应的设定上可分为固定效应模型和随机效应模型两大类.从空间效应的设定形式上可分为空间滞后回归(空间自回归)和空间误差自回归两种形式.目前的研究大都假定了因变量与自变量的关系为参数结构特别是线性形式,即线性空间面板数据模型.实际问题分析时因变量与自变量之间往往不仅仅是线性关系,而是更为复杂的形式.模型形式的错误设定会导致后面推断结果偏离实际情况.为了更好的探求因变量与自变量之间蕴含的复杂关系,提高模型的灵活性,多种非参数和半参数建模方法在近二十年来相继被提出,并被应用到各类复杂数据分析中.常见的半参数模型有部分线性模型、变系数模型、可加模型和单指标模型以及它们的混合形式等.[4-5]

最近,利用半参数建模方法分析空间面板数据开始得到关注,已经有多类半参数空间面板数据模型被提出.HU等[6]提出了一类部分线性空间误差自回归固定效应面板数据模型,ZHANG和SUN[7]还有AI和ZHANG[8]分别研究了两类部分线性空间滞后回归固定效应面板数据模型,BAI等[9]研究了一类部分线性变系数空间误差自回归面板数据模型,ZHANG和SHEN[10]则提出了部分线性变系数空间滞后随机效应面板数据模型.上面几篇文献都是基于级数(样条)方法构造了模型的估计.陈建宝等[11]将变系数模型结构和空间自回归面板数据模型结合起来,研究了一类变系数空间自回归固定效应面板数据模型,采用基于局部线性方法的profile似然方法估计其中的未知空间自回归系数和系数函数,并给出了所提估计量的渐近性质.

对于半参数空间面板数据模型来说.回归系数的显著性检验,固定效应或随机效应的检验以及误差序列相关或异方差问题的检验都非常重要.除了这些检验问题之外,对于空间效应是否存在的检验更是一个核心问题.本文将基于陈建宝等[11]讨论的变系数空间自回归固定效应面板数据模型研究这一问题,该模型可记为如下形式

针对模型(1.1),空间效应的检验记为如下的假设检验问题

对于空间自回归系数的检验问题,经典线性空间自回归面板数据模型大都采用的是拉格朗日乘子检验方法(Rao’s Score方法),因为这种方法在构造检验统计量时只需要模型在原假设成立时的估计,避免了备择假设下复杂的极大似然估计计算.[16-19]然而,对于模型(1.1)的检验问题(1.2),由于非参数系数函数的存在,我们无法直接构造拉格朗日乘子检验统计量.对于这一问题,LI和MEI[20]以及GUO和WEI[21]将FAN等[22]提出的广义似然比检验方法用到了截面数据下部分线性空间自回归模型以及变系数空间自回归模型的检验问题上.本文将该方法推广到面板数据模型(1.1)上.

2.Profile极大似然估计

为了构造检验统计量,下面先介绍模型(1.1)的估计,采用的是文[11,23]中的估计方法.

定义如下的矩阵形式

3.Profile广义似然比检验

在备择假设H1下,可以得到profile对数似然函数为

4.数值模拟

下面将通过数值模拟来验证所提检验方法的有效性,同时也一起考察第二节所用估计方法的有效性.

假定研究区域是边长为m-1个距离单位的正方形,n个空间观测单元正好在m×m个格子点上,权重矩阵W设定为Rook矩阵和Queen矩阵两种形式.考虑如下变系数空间自回归固定效应面板数据模型的估计和检验

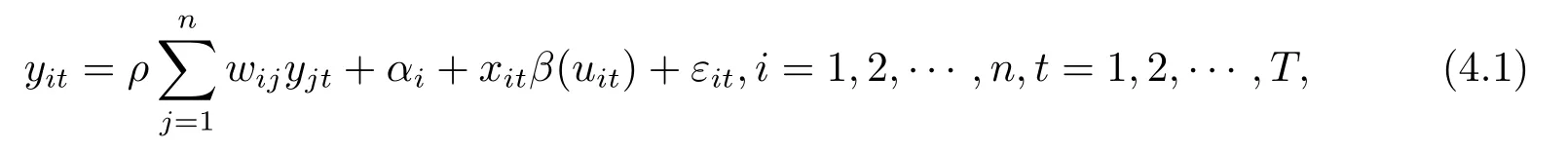
其中设定n=m2,xit～N(1,1),uit～U(0,1),固定效应αi～U(0,1),i=2,···,n.系数函数β(uit)=2*sin(2πuit)-1.权重矩阵分别采用Rook矩阵和Queen矩阵.

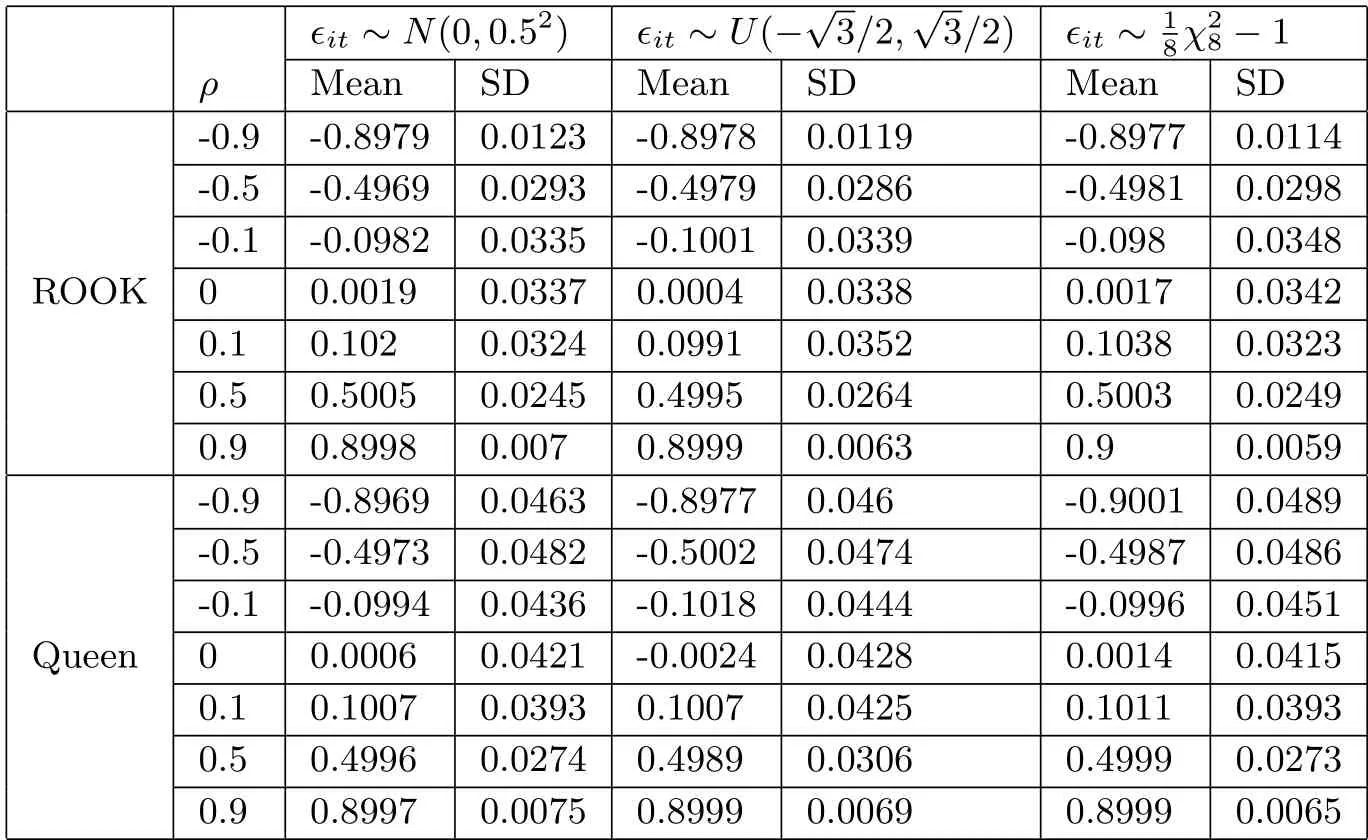
表4.1 n=64时ρ的估计

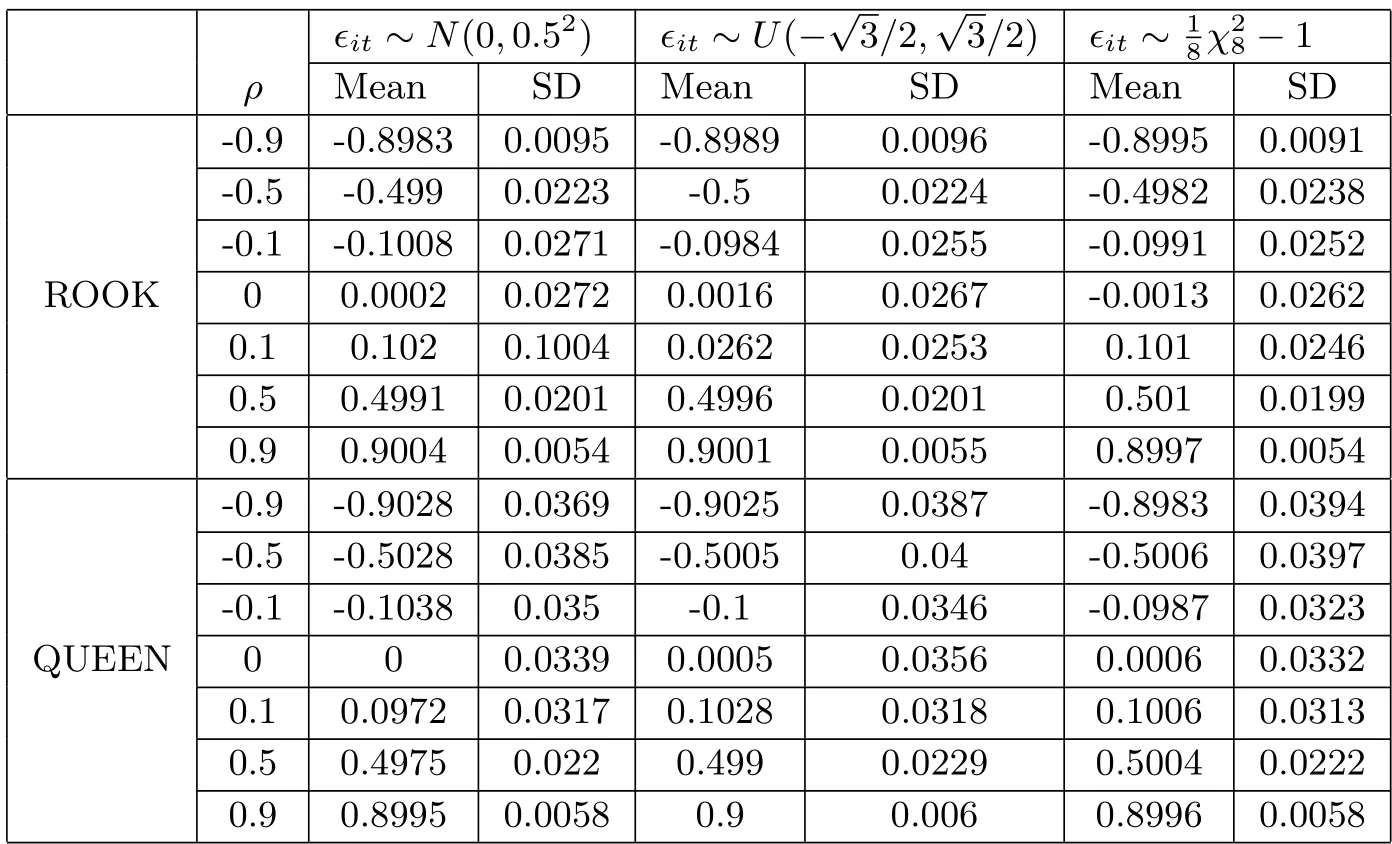
表4.2 n=100时ρ的估计

为了考察不同残差分布设定对模型估计效果的影响,我们对误差项的分步作如下设定,且满足均值为0,方差为0.25,即1)εit～N(0,0.52);2)εit～-1.在模拟中,选择高斯核函数K(z)=窗宽h取su(nT)-1/5,其中su是u11,u12,···,unT的样本标准差.样本量分别取n=64,100,令时间维度T=3,ρ=±0.9,±0.5,±0.1,0,针对每种设定,模拟重复500次,每次都利用前面介绍的估计方法给出参数分量和非参数分量的估计.对于参数分量ρ,以MEAN和SD分别表示其500次估计值的均值和标准差,模拟结果见表4.1和表4.2.我们发现在误差项ε在均值为0、方差为0.25的相同条件下,无论模型误差ε服从何种分布,无论是Rook矩阵还是Queen矩阵,ρ的估计值都几乎等于真实值,且随着样本量n的增大,ρ的估计值越接近真实值,偏差和标准差也越小,且均小于0.01.

表4.3 n=64时系数函数的RASE

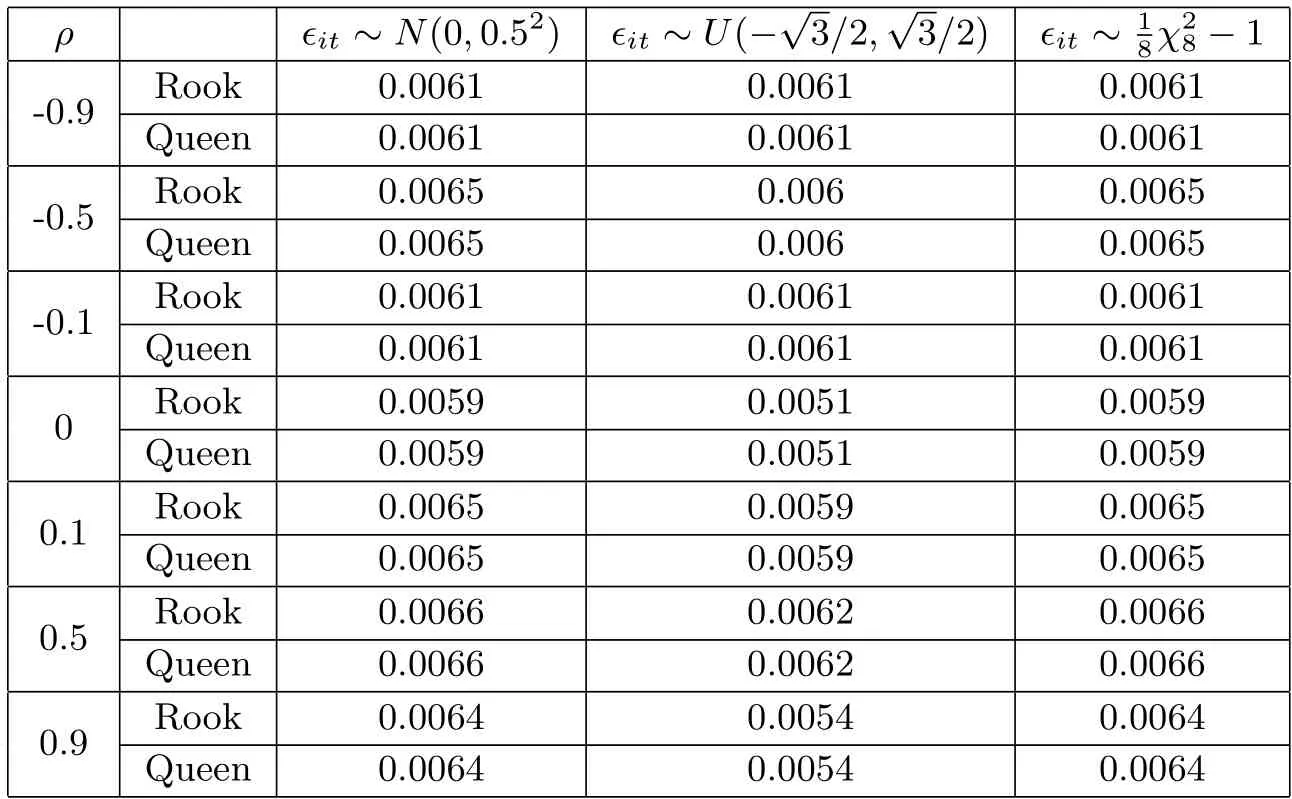
表4.4 n=100时系数函数的RASE

对于未知系数函数β(·),利用如下的根均方误差(RASE)考察其表现,

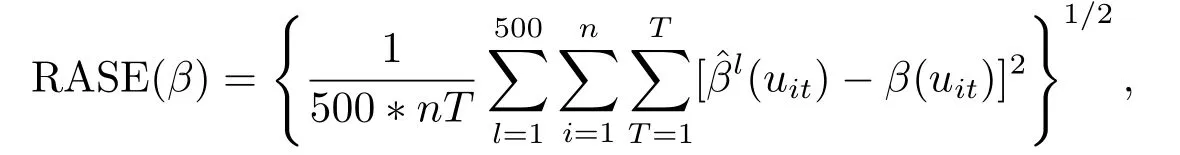
依据模型(4.1),设定循环次数N=500,T取3和5,样本量分别取64和100,ρ=±0.15,±0.1,±0.05,0.显著性水平α=0.05.设定m=500的bootstrap样本来计算p值,结果见表4.5和表4.6.通过模拟结果,可以得出如下结论：

1) 当零假设为真时(即ρ=0),无论样本量n为64还是100的情况下,拒绝率都非常接近显著性水平0.05.而当零假设不为真时即ρ/=0,即备则假设条件下,拒绝率随着越来越背离原假设而增大.

2) 在误差项ε的均值为0,方差为0.25情况下,无论误差向服从三种分布中的哪一种,Rook矩阵还是Queen矩阵,检验结果ρ值的总体情况并无太大差异.由此可见所用的Bootstrap对不同的误差分布有着稳健性.

表4.5 n=64时基于GLR检验的原假设拒绝频率

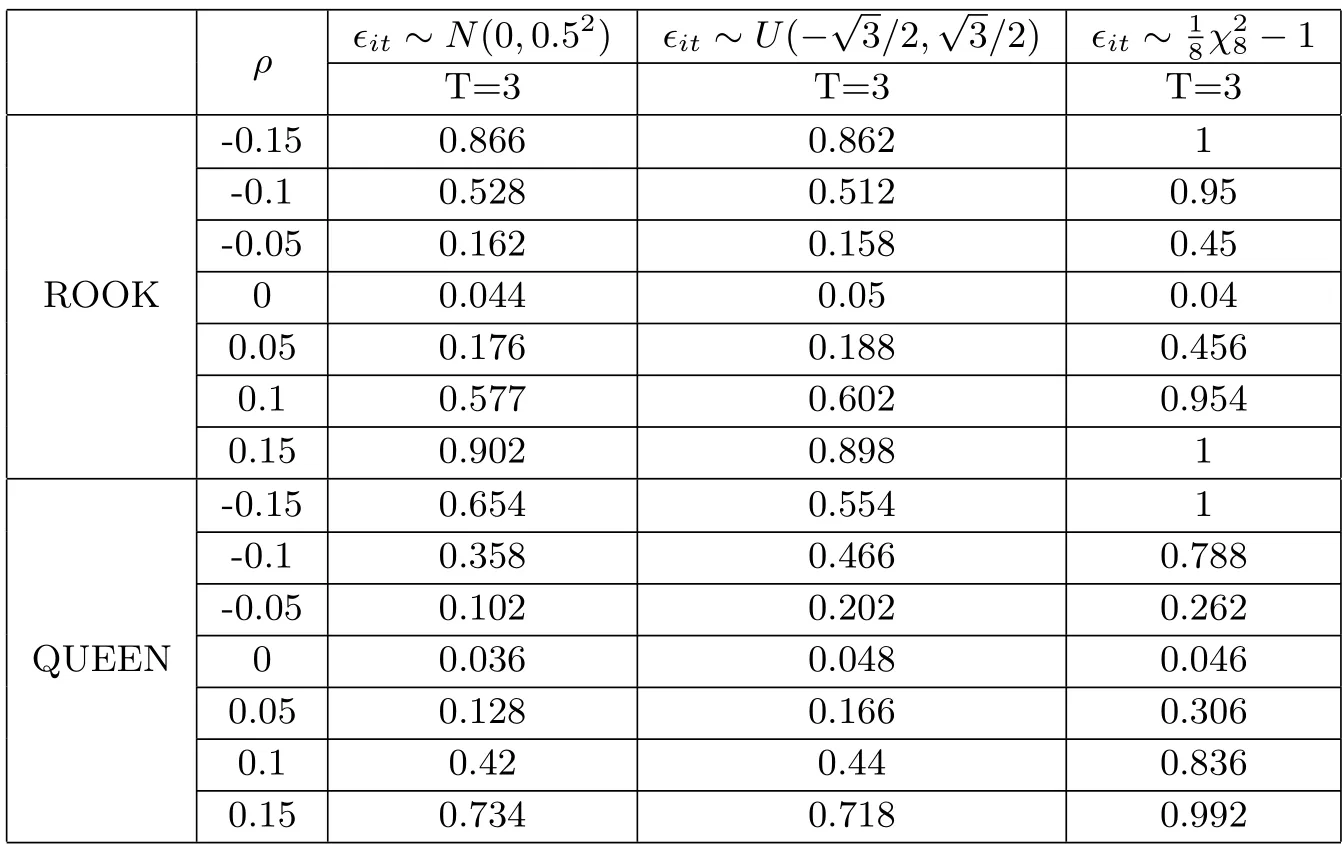
表4.6 n=100时基于GLR检验的原假设拒绝频率

5.结论

针对固定效应变系数空间自回归面板数据模型,本文主要研究了空间效应的检验问题,构造了广义似然比检验统计量,并利用bootstrap方法进行检验p值的计算,数值模拟结果验证了所提方法在有限样本下的有效性.该方法可以直接推广到其它类型的半参数面板数据模型上.由于模型本身的复杂性,论文没有给出所构造检验统计量的渐近分布,而是借助于bootstrap方法计算检验p值,这也是在半参数模型领域常用的做法.另外本文只是考虑了空间效应的检验,对于其他类型的检验问题,还需要进一步研究.