(1+1)维色散长波系统的留数对称和相互作用解

张开开,夏亚荣

(西安建筑科技大学理学院,陕西 西安 710055)

1.引言

非线性偏微分方程在物理学、力学以及各类工程技术科学等领域发挥着重要作用,尤其是在物理的各个分支领域受到越来越多学者们的关注,如流体力学、等离子体理论、非线性光学和量子场论等[1-2].对称分析在求解非线性偏微分系统中起着重要作用,利用经典或非经典的Lie群方法[3],可以获得微分方程的Lie点对称,并通过有限变换将已知解转化为新解,通过相似约化构造群不变解.近年来,楼森岳教授发现对于任意一个Painlev´e可积的非线性系统,在Painlev´e截断展开时,奇异流形的负一次幂的系数就是该系统的非局域对称,也被称为留数对称[4].由于非局域对称是无法直接求解的,楼等人[5]为解决该问题,提出将初始系统进行延拓的直接方法,通过引入新的辅助因变量使得初始系统局部化为Lie点对称,然后通过Lie第一基本定理得出封闭系统的有限对称变换群.另外,楼森岳教授对tanh函数展开法和Riccati方程展开法进行了推广,并构造出求解非线性系统的CRE方法和CTE方法[6-7],这对寻找更多非线性系统的可积性提供了可能.

文[8]基于Painlev´e截断展开研究了广义色散水波系统的留数对称、n阶B¨acklund变换,并运用CTE方法求解出孤子与共振波、周期波、有理函数波和误差函数波之间的相互作用解;文[9]基于标准的Painlev´e截断展开导出了(2+1)维色散长波系统的留数对称、B¨acklund变换,研究了该系统的CRE可解性、孤子-椭圆波解和守恒律;文[10]利用Painlev´e截断展开法构造了(2+1)维色散长波方程的非局域对称、B¨acklund变换,并从CRE方法出发研究了孤子-椭圆波相互作用解.本文主要考虑(1+1)维色散长波系统的留数对称、局部化、B¨acklund变换、CRE可解和相互作用解,具体方程组如下:

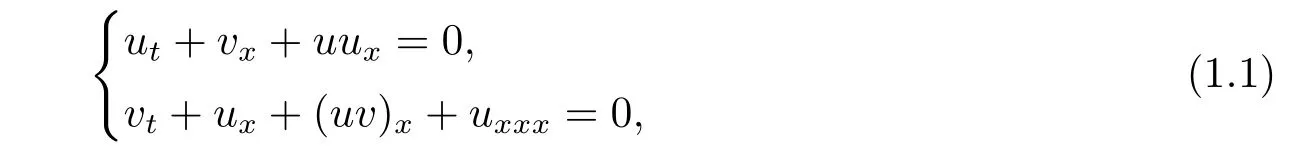
其中,沿x轴传播的水平速度u(x,t)和未受扰动水面上波的高度v(x,t)分别是x和t的可微函数.在文[11]中利用齐次平衡法得到系统(1.1)的多孤子解.

本文具体工作安排如下: 第二部分基于Painlev´e截断展开法解出(1+1)维色散长波系统的留数对称,并给出该系统对应的有限对称变换群;第三部分证明了(1+1)维色散长波系统是CRE可解的,并利用CRE方法的特殊形式CTE方法求出该系统的相互作用解,同时选取适当的参数对上述解作出图像模拟;第四部分是对本文的总结和讨论.

2.(1+1)维色散长波系统的留数对称

定义2.1给定一个非线性偏微分方程

若它的解u具有如下的洛朗展开式:

并满足

1)α是一个整数(领头项分析确定);

2)uj=uj(t,z1,z2···zn)(j=1,2,···)在流形φ(z1,z2···zn)的邻域内解析;

3)uj(j=1,2,···)满足方程自相容的解.则称非线性偏微分方程(2.1)具有Painlev´e性质.

对于任意一个具有Painlev´e性质的非线性偏微分方程(2.1)都可以做如下截断Painlev´e展开,

其中α是通过领头分析而确定的正整数.

而方程(2.1)的一个对称σ满足下面方程

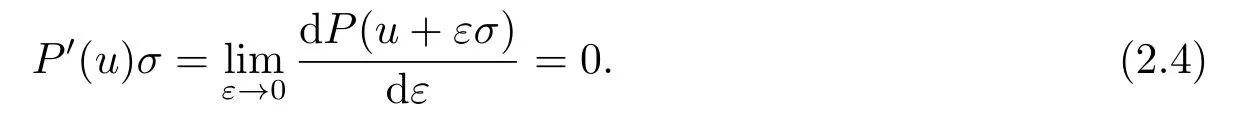
把展开式(2.3)代入原方程(2.1)中,消去φ的各次幂的系数,我们可得如下定理.

定理2.1(留数对称定理)Painlev´e截断展开式(2.3)中奇异流形的留数uα-1关于原方程(2.1)的解uα是一个对称.

证将(2.3)代入原方程(2.1)中,我们有

分别消去φ0和φ-1可得

由对称定义可知uα是原始系统的解,奇异流行的留数

是关于解uα的一个对称,故定理2.1 得证.

对于一个Painlev´e可积的非线性偏微分方程(2.1),我们通过变换

可以把原方程(2.1)转化为它的Schwarzian形式

Schwarzian形式(2.10)在M¨obious变换

下是不变的,这意味着方程(2.10)具有三个对称σφ=d1,σφ=d2φ和

其中d1,d2和d3为任意常数.

根据以上讨论我们可以知道留数对称就是关于线性化方程(2.9)的M¨obious变换的对称(2.12),也就是说留数对称可以局部化为

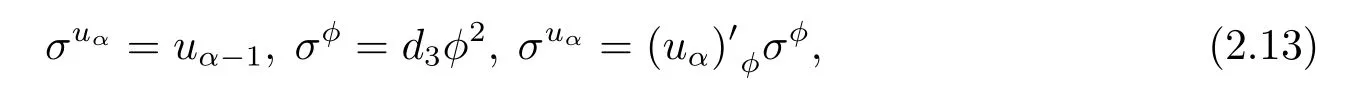
对于不同的模型,d3的取值不同.

现通过齐次平衡法平衡(1+1)维色散长波系统的最高阶导数项和非线性项,我们可以得到系统(1.1)的Painlev´e截断展开式为

其中u0,u1,v0,v1,v2和奇异流行φ都是关于x和t的函数.把(2.14)式代入(1.1)式中消去的各次幂的系数可以得到

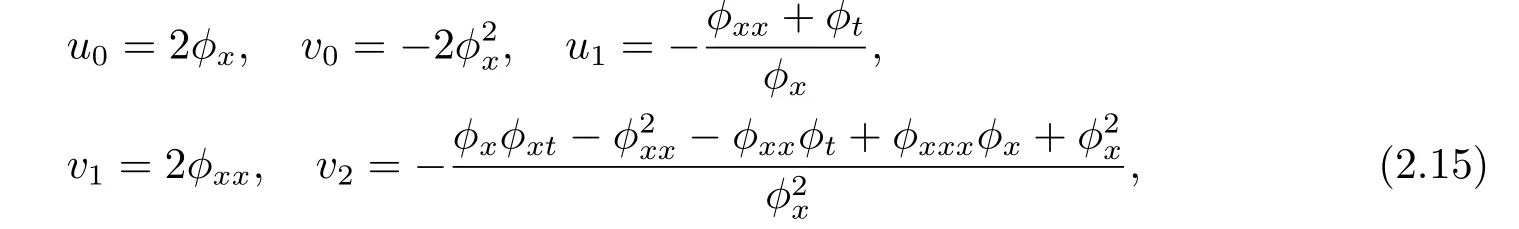
并且φ满足系统(1.1)的Schwarzian方程

把(2.14)式和(2.15)式代入系统(1.1)中我们可以得到如下的非自B¨acklund变换.

定理2.2如果φ是Schwarzian方程(2.16)的解,那么

是系统(1.1)的解.

定理2.3(1+1)维色散长波方程组系统(1.1)的留数对称为:

证方程组(1.1)对应的线性化方程为:

利用(2.16)把(2.17)和(2.18)代入(2.19)中,则(2.19)俩端恒成立,故该定理得证.

系统(1.1)的留数对称σu=2φx,σv=2φxx对应的初值问题为:

这里ε为无穷小参数.由于函数φ和φ的导数的存在,导致系统(1.1)的留数对称(2.18)不是一个封闭系统,即留数对称是非局部对称,因此对应的初值问题是无法求解的,所以我们需引入俩个新的辅助因变量

使得非局域对称局部化为下列Lie点对称

从方程(2.22)可以看出,在由(1.1)、(2.16)和(2.21)构成的延拓系统中,非局部的留数对称已转化为了局部对称,且方程(2.22)的Lie点对称的向量场表示为:

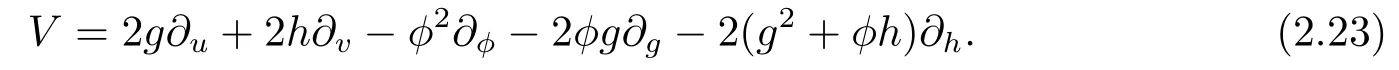
根据Lie第一基本定理,求解以下初值问题:

通过求解上述初值问题,可以得到如下的有限对称变换定理:

定理2.4(自B¨acklund变换定理) 若{u,v,φ,g,h}是延拓系统(1.1)、(2.16)和(2.21)的一个解,则也是该延拓系统的一个解,其中,

注2.4由定理2.4我们可以知道,通过Painlev´e截断展开得到的留数对称σu=2φx,σv=2φxx正好是群(2.25)的无穷小形式.因为奇异流行系统(1.1)、(2.16)和(2.21)在变换1+εφ →φ(εg →φx,εh →φxx)下是保持不变的.因此以上的群变换实际上等价于把表达式(2.15)代入(2.14)后的Painlev´e截断展开式.

3.(1+1)维色散长波系统的CRE可解性和相互作用解

由于留数对称得到的解是一个特殊的群不变解[12],为了找到初始系统(1.1)更一般的解,我们将留数对称方法进一步推广到CRE方法,并证明系统(1.1)是CRE可解的.其次,通过CRE方法的特殊形式CTE方法得到孤子-椭圆余弦波的相互作用解.

Ⅰ CRE可解

对于一个给定的非线性偏微分方程

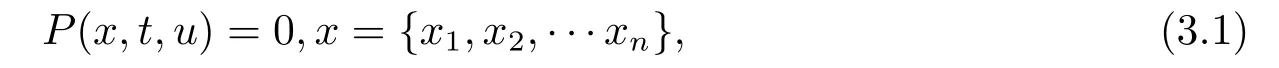
我们的目的是寻找如下截断展开形式的解,

其中u,w是x,t的函数,n是通过平衡方程(3.1)的非线性项和最高阶导数项而确定的正整数,R(w)满足如下的Riccati方程

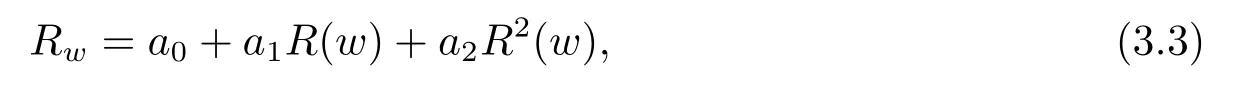
其中a0,a1和a2是常数.将(3.2)及(3.3)代入(3.1)中得到关于R(w)的方程,令R(w)的各次幂的系数为零,则可解出ui的关系式.

定义3.1对于非线性方程(3.1),若将表达式(3.2)及(3.3)代入(3.1)后,通过消去R(w)各次幂的系数得到的ui和w的方程是相容的,不是超定的,我们则称表达式(3.2)是相容的Riccati展式(CRE),且非线性系统(3.1)是CRE可解的.

基于CRE方法,(1+1)维色散长波系统(1.1)的解可以表示为

其中u0,u1,v0,v1,v2是x,t的函数,且R(w)为Riccati方程(3.3)的解.

把(3.3)式与(3.4)式代入系统(1.1)中,消去R(w)各次幂的系数可得

且函数w满足系统(1.1)的Schwarzian方程

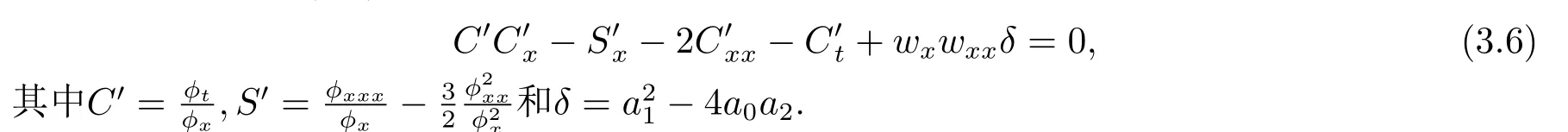
综上所述,(1+1)维色散长波系统(1.1)具有一个相容Riccati展式,故系统(1.1)是CRE可解的.系统(1.1)的相容Riccati展式如下:

其中u0,v0满足方程(3.5).

Ⅱ (1+1)维色散长波系统的CTE可解性和相互作用解

当a0,a1,a2分别为1,0,-1时,Riccati方程(3.3)具有一个特殊解R(w)=tanh(w),此时,CRE 可解为CTE可解,并且系统(1.1)的相容tanh函数展开式为:

其中a0=1,a1=0,a2=-1,u0,v0分别由方程(3.5)给出.

为了求解系统(1.1)与其它非线性波之间的相互作用解,我们只需要找到w方程(3.6)的解,而刻画孤子和椭圆波的相互作用解w具有如下特殊形式：

其中S=sn(h2x+k2t,m),D=dn(h2x+k2t,m),T=tanh(h1x+k1t+cEllipticF(S,m)),R=cosh(h1x+k1t+cEllipticF(S,m)).

现在取参数{h1=0.8,k1=0.8,h2=1.5,k2=2.4,c=1.58,m=0.8},则u和v的图像模拟分别如图1(a)-1(c)和图2(a)-2(c)所示.

图1 (a) u(x,0)沿x轴的波形图

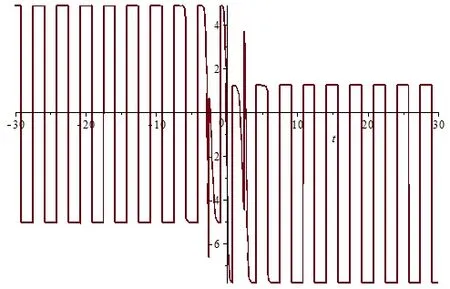
图1 (b) u(0,t)沿t轴的波形图

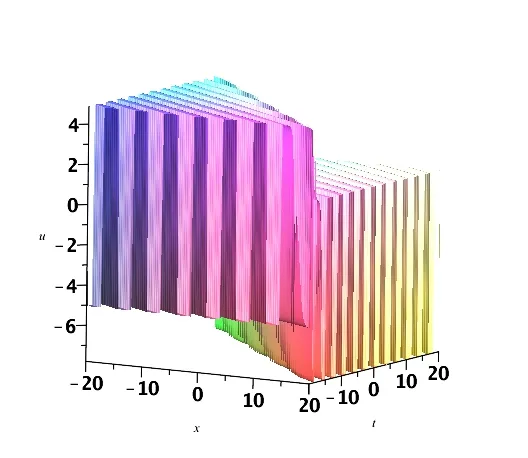
图1 (c) u(x,t)的三维波形图

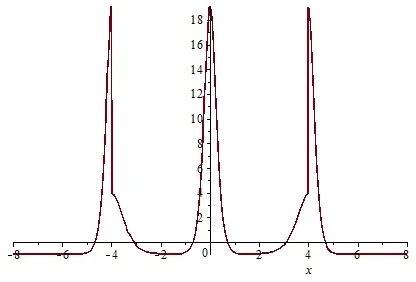
图2 (a) v(x,0)沿x轴的波形图

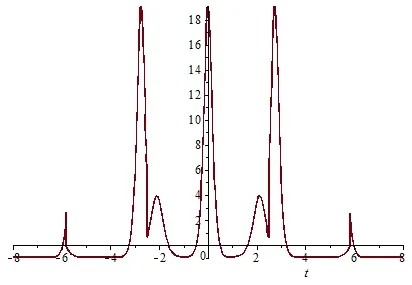
图2 (b) v(0,t)沿t轴的波形图

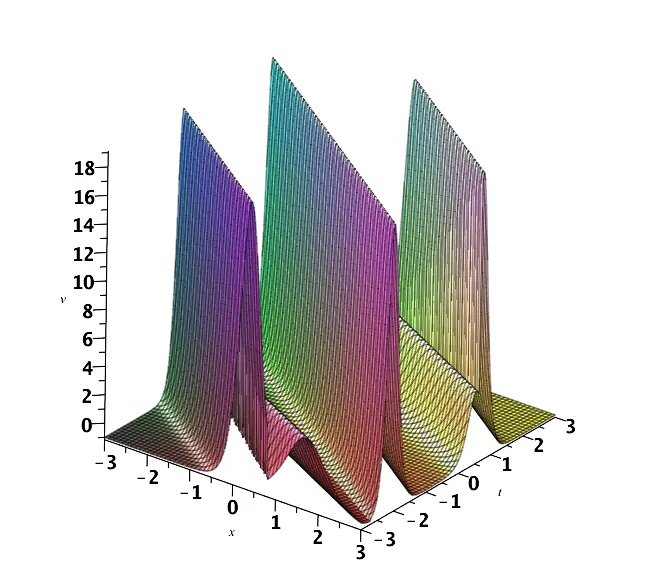
图2 (c) v(x,t)的三维波形图

把(3.14)或(3.15)代入(3.12)中可得

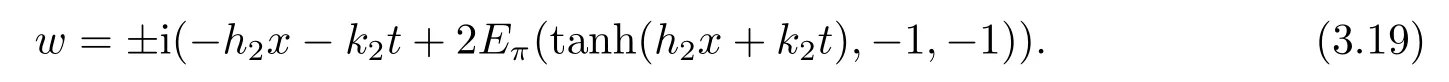
把(3.19)和(3.5)代入(3.8)中可得孤子-椭圆余弦波解u和v分别为

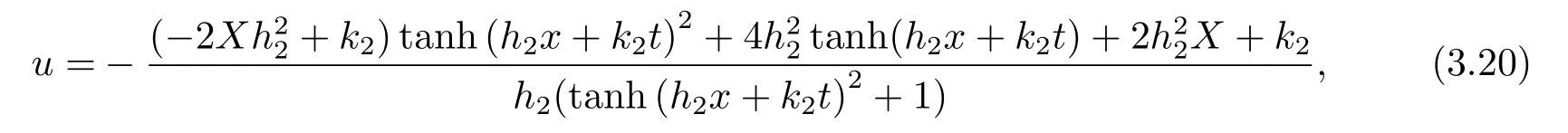
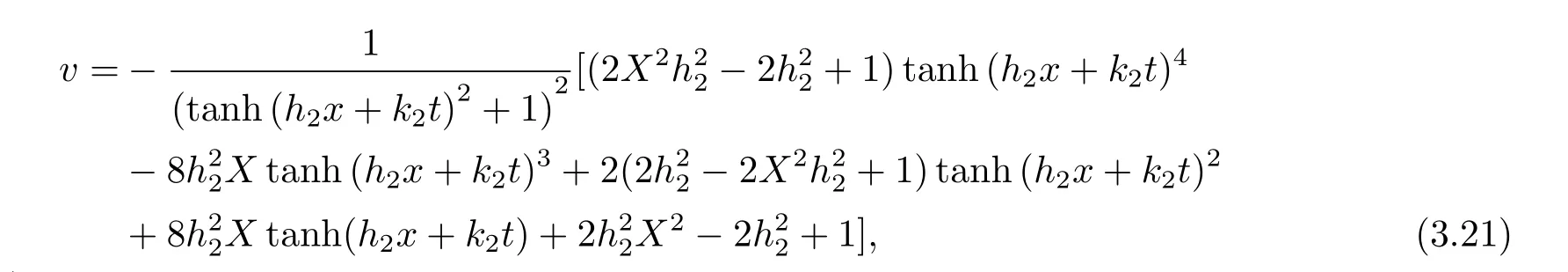
其中X=tan(h2x+k2t-2Eπ(tanh(h2x+k2t),-1,1)).

在(3.20)式和(3.21)式中取参数{h2=0.000005,k2=0.000004},则u和v的图像模拟分别如图3(a)-3(c)和图4(a)-4(c)所示.

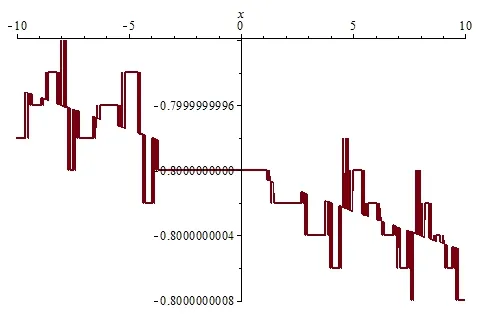
图3 (a) u(x,0)沿x轴的波形图

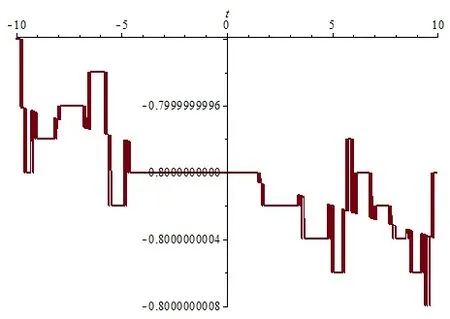
图3 (b) u(0,t)沿t轴的波形图

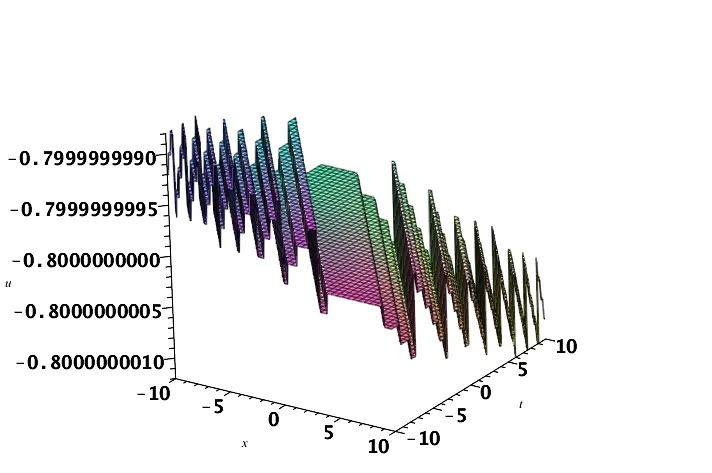
图3 (c) u(x,t)的三维波形图

图4 (a) v(x,0)沿x轴的波形图

图4 (b) v(0,t)沿t轴的波形图

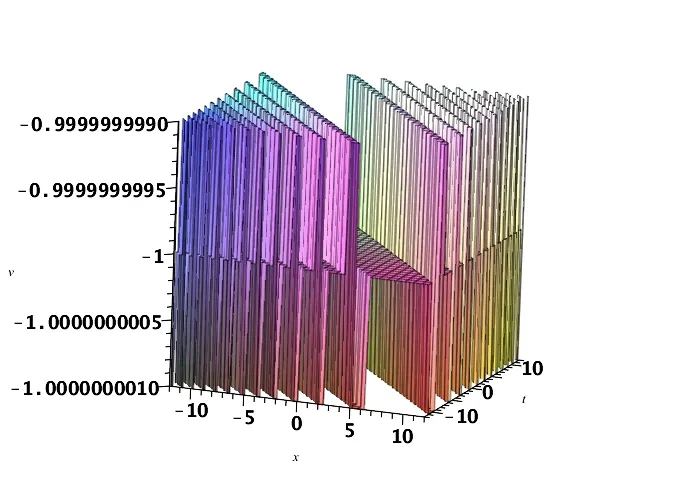
图4 (c) v(x,t)的三维波形图

现在另取方程(3.6)的第二类孤子-椭圆波的相互作用解w的形式为:

其中sn(z,m)为雅克比椭圆正弦函数.

把(3.22)式代入(3.6)式中可得

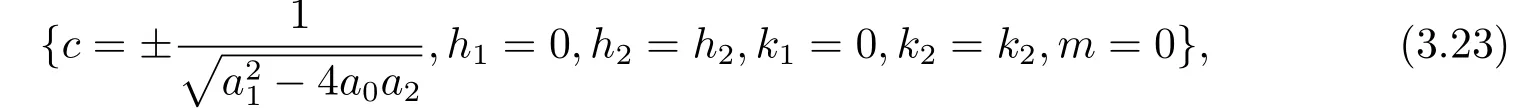
其中h2和k2为任意常数.

把(3.23)式代入(3.22)式中,其结果如下:

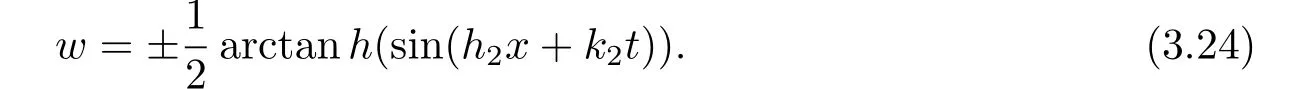
把(3.24)和(3.5)代入(3.8)式中可得系统(1.1)的孤子-椭圆余弦波解u和v分别为

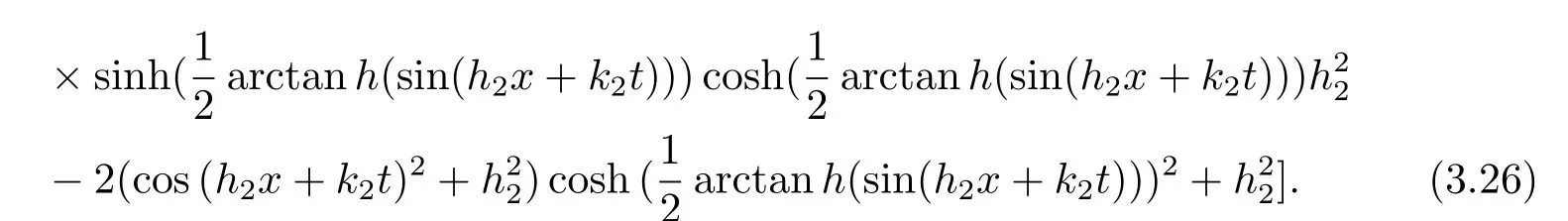
现对(3.25)式和(3.26)式选取参数{h2=0.000000005,k2=0.000000005},则u和v的图像模拟分别如图5(a)-5(c)和图6(a)-6(c)所示.

图5 (a) u(x,0)沿x轴的波形图

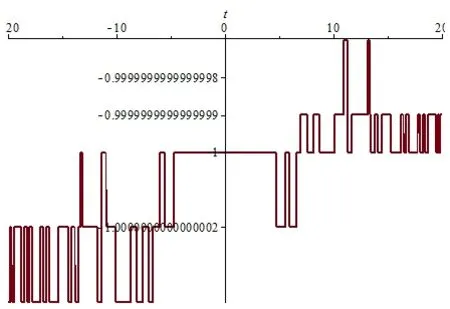
图5 (b) u(0,t)沿t轴的波形图

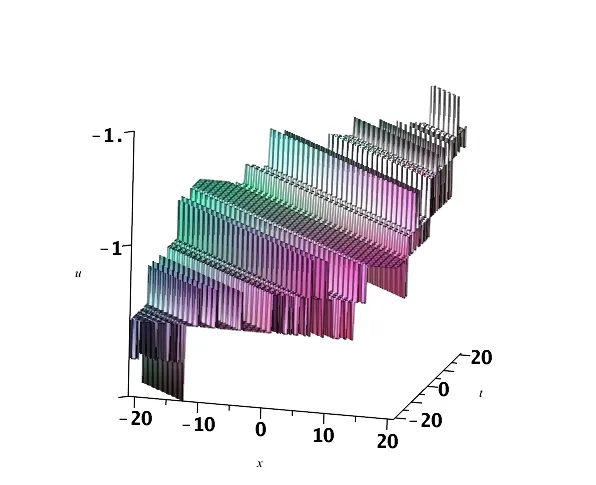
图5 (c) u(x,t)的三维波形图

图6 (a) v(x,0)沿x轴的波形图

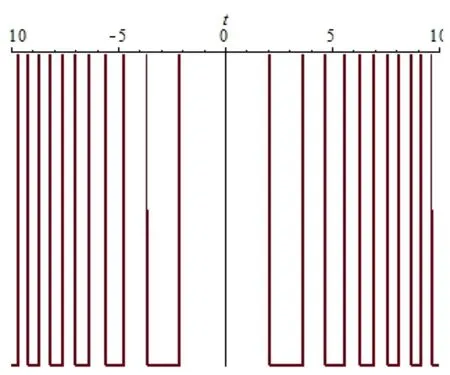
图6 (b) v(0,t)沿t轴的波形图

图6 (c) v(x,t)的三维波形图

4.总结和讨论

本文研究了(1+1)维色散长波系统的留数对称和孤子-椭圆周期波之间的相互作用解.基于Painlev´e截断展开得到初始系统的留数对称,然后通过引入辅助因变量将留数对称局部化为Lie点对称,并由Lie第一基本定理给出封闭系统的有限对称变换.此外,利用Riccati方程证明了(1+1)维色散长波系统是CRE可解的,并运用CRE方法的特殊形式CTE方法解出孤子-椭圆周期波之间的相互作用解.由于留数对称是线性函数,且Schwarzian方有无穷多解,因此该系统的无穷多个留数对称和n阶B¨acklund变换值得我们进一步研究.更多类型的数学物理方程的可积性和相互作用解有待我们进一步发现.