Trudinger-Moser Inequality Involving the Anisotropic Norm with Logarithmic Weights in Dimension Two
ZHU Maochun(朱茂春),CHEN Wenhuan(陈文欢)
(School of Mathematical Sciences,Jiangsu University,Zhenjiang 212013,China)
Abstract:In this paper,we investigate the Trudinger-Moser inequality which involves the anisotropic Dirichlet norm for radial Sobolev spaces with logarithmic weights in dimension two.By establishing a critical radial lemma and the famous Leckband functional equality,we find that the precise Trudinger-Moser growths depend on the logarithmic terms,and we determine the corresponding sharp Moser type exponents.In a particular case,we observe a critical Trudinger-Moser growth of double exponential type in the limiting case β=1.The optimal of best constant of the Trudinger-Moser inequality with logarithmic weights is proved by constructing suitable test functions sequence.
Key words:Anisotropic;Radial;Logarithmic weight;Trudinger-Moser inequality
1.Introduction
LetΩdenote a bounded domain in R2,and denote(Ω)the standard first order Sobolev space given by


In this paper,we organize the paper as follows.In Section 2,we prove an important Radial Lemma.In Section 3,we convert the two-dimensional problems into one-dimensional by using the radial lemma,and finish the proof of Theorem 1.1 by the famous Leckband’s inequality.Furthermore,we also show that the functions inare bounded whenβ >1.In Section 4,we discuss the limiting caseβ=1 and obtain a critical growth of double exponential type,that is,Theorem 1.2.
Throughout this paper,the lettercalways denotes some positive constant which may vary from line to line.
2.An Important Lemma-Radial Lemma
We first collect some important properties of the functionF(x) and its polarF0(x) in[23] which will be used in the following:
Lemma 2.1[23]The functionF(x) and its polarF0(x) satisfy:


3.Trudinger-Moser Inequality Involving the Anisotropic Norm with Logarithmic Weights in the Case β∈[0,1)
In this section,we prove the Trudinger-Moser inequality involving the anisotropic norm with logarithmic weights.
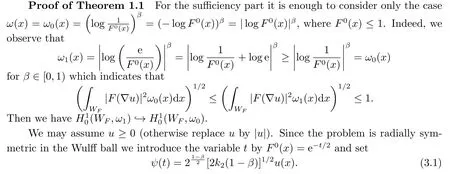




4.Trudinger-Moser Inequality Involving the Anisotropic Norm in the Limiting Case β=1
In this section we discuss the limiting caseβ=1,i.e.,weights of the form log.As stated in Theorem 1.2 we obtain a critical growth of double exponential type.
Proof of Theorem 1.2(a) can be proved with the same argument used in the first part of Theorem 1.1.

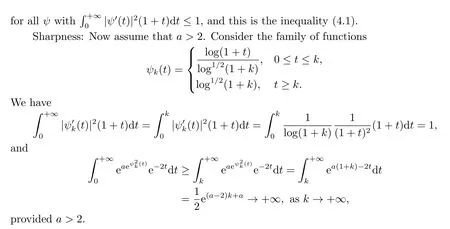
- 应用数学的其它文章
- 一类线性离散时间系统的预见控制器设计
- Global Boundedness to a Quasilinear Attraction-repulsion with Nonlinear Diffusion
- 关于非齐次树指标m重马氏信源的一个强极限定理
- 相依风险结构下弹性ò休c金产品价Š风险比较
- Superconvergence Analysis of Anisotropic Linear Triangular Finite Element for Multi-term Time Fractional Diffusion Equations with Variable Coefficient
- Infinitely Many Sign-changing Solutions for a Quasilinear Choquard Equation

