关于非齐次树指标m重马氏信源的一个强极限定理
2022-10-31 12:39金少华田雪然
应用数学 2022年4期
金少华,田雪然
(河北工业大学理学院,天津 300401)
1.引言
树指标随机过程已成为近年来发展起来的概率论的研究方向之一.强极限定理一直是国际概率论界研究的重要课题.杨等人在文[1]中给出了关于树指标非齐次马氏链的广义熵遍历定理.ZHONG等在文[2]中通过引入树指标马尔科夫链的概念,证明了Cayley树指标下马尔科夫链关于二元函数延迟和的一个强极限定理.ZHONG等在文[3]中首先引入渐近对数似然比作为二叉树上任意随机场与分叉马尔科夫链之间偏差的度量,然后通过构造一个非负鞅,建立了二叉树指标马尔科夫链的一类强偏差定理.WANG等在文[4]中给出了连续状态非齐次马氏链滑动平均的强大数定律.李世林等人在文[5]中研究了在有限状态空间取值的二叉树上非齐次马氏链转移概率调和平均的极限性值.金少华等人在文[6]中给出了非齐次树上马氏双链转移矩阵的一个强极限定理.本文通过引入相对熵密度偏差的概念和构造非负鞅,研究给出了关于非齐次树指标m重马氏信源的一个强极限定理.
2.基本概念
设T是一个具有根顶点o的无限树,{Nn,n ≥1}是一列正整数集,如果T的第n(n ≥0)层上的每个顶点均与第n+1层上的Nn+1个顶点相邻,则称T为广义Bethe树或广义Cayley树.特别地,若对非负整数集N,用模m的同余关系对其分类得到如下模m的剩余类
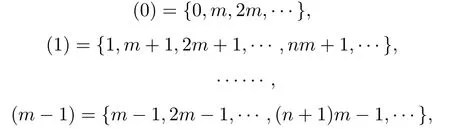

3.强极限定理




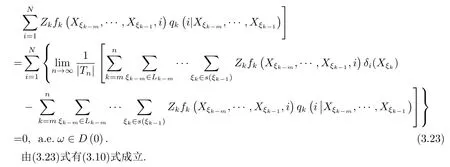
猜你喜欢
电子制作(2022年16期)2022-09-23
数学物理学报(2022年2期)2022-04-26
数学物理学报(2021年3期)2021-07-19
现代计算机(2021年14期)2021-07-09
计算机与数字工程(2020年8期)2020-10-14
杂文月刊(2019年14期)2019-08-03
——基于二叉树的图像加密
数字通信世界(2019年4期)2019-06-03
名作欣赏(2017年32期)2017-11-28
杂文月刊(2017年18期)2017-11-12
领导文萃(2016年6期)2016-12-26
- 应用数学的其它文章
- 一类线性离散时间系统的预见控制器设计
- Global Boundedness to a Quasilinear Attraction-repulsion with Nonlinear Diffusion
- Trudinger-Moser Inequality Involving the Anisotropic Norm with Logarithmic Weights in Dimension Two
- 相依风险结构下弹性ò休c金产品价Š风险比较
- Superconvergence Analysis of Anisotropic Linear Triangular Finite Element for Multi-term Time Fractional Diffusion Equations with Variable Coefficient
- Infinitely Many Sign-changing Solutions for a Quasilinear Choquard Equation

