浅论函数奇偶性的判断方法

335500 江西省万年县万年中学 徐 广

335500 江西省万年县万年一中 李 敏

函数的奇偶性是函数的重要性质，也是高考的重点与热点，更是广大高中生的易错点．学好函数的奇偶性一直是广大高中生的诉求，要掌握好函数奇偶性的判断方法，可以从以下三个方面入手．

一、 关于函数奇偶性的定义

北师大版高中数学教材中关于函数奇偶性的定义简述如下.

设函数y=f(x)，x∈I，且对任意x∈I，恒有-x∈I(即定义域要关于原点对称)，(1)若f(-x)=-f(x)，则称y=f(x)为奇函数；(2)若f(-x)=f(x)，则称y=f(x)为偶函数．

上述定义从理论上说明，定义域关于原点对称是函数具有奇偶性的一个前提．相当一部分学生常常忽视所给函数的定义域，直接用函数奇偶性的判别式确定其奇偶性，很容易得出错误的结论．

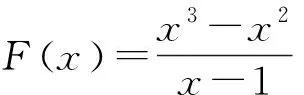
错解：由题意可得F(x)=x2，从而有F(-x)=F(x)，所以y=F(x)为偶函数．

评析：上述解答没有求出函数的定义域，忽视了判断函数的定义域是否关于原点对称．

正解：因为y=F(x)的定义域为(-∞,1)∪(1,+∞)，不关于原点对称，所以y=F(x) 不具有奇偶性．

因此，教师在讲授新课时，一定要强调定义域关于原点对称的重要性与先决性．

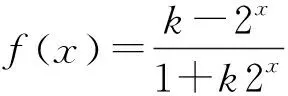
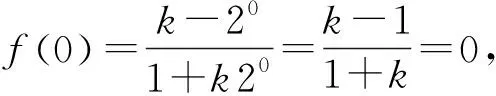
评析：上述解法没有考虑0是否属于f(x)的定义域，而是默认f(x)在x=0处有定义．

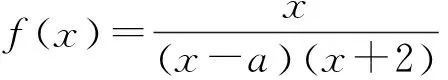
解析：注意到函数的定义域要关于原点对称，已知x≠-2且x≠a，所以要保证定义域对称，则a=2，这是f(x)为奇函数的必要条件，经验证，符合题意．

二、 函数奇偶性的四则运算合成

在掌握了初等函数的奇偶性后，对于给定的复杂函数的奇偶性，往往不需要直接用定义方法来证明或判断，而是用合成方法处理．

设在公共定义域内，函数f(x)和f0(x)为奇函数，而g(x)与g0(x)为偶函数，k，c为常数，则有如下结论.

(1)当k≠0时，y=kf(x)为奇函数，y=kg(x)为偶函数．特别地，当k=0时，y=kf(x)和y=kg(x)既是奇函数也是偶函数．

(2)当c≠0时，y=f(x)+c不是奇函数,y=g(x)+c为偶函数．

(3)y=f(x)±f0(x)为奇函数，y=g(x)±g0(x)为偶函数．

(5)y=f(x)f0(x)为偶函数，y=g(x)g0(x)为偶函数．

(6)y=f(x)g(x)为奇函数．

(7)设h(x)=kf(x)+cg(x)(其中f(x)不为偶函数，g(x)不为奇函数),若h(x)为奇函数，则c=0；若h(x)为偶函数，则k=0.

例4判断下列函数的奇偶性．

例5设F(x)=x3+(t-1)x2为R上的奇函数，求实数t的值．

解：由题意可得t-1=0，即t=1．

这里可以直接省去用F(-1)=-F(1)计算得出结果，或者由计算稍微复杂的F(-x)+F(x)=0推导得到结果．

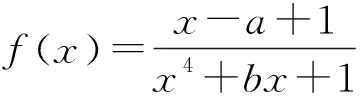
分析：因为f(x)在x=0处有定义，所以f(0)=0，可得a=1，所以分子为x，是奇函数，而f(x)为奇函数，所以分母x4+bx+1必须为偶函数，即有b=0．

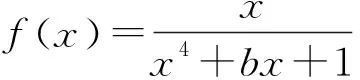
这里主要应用了函数y=0既是奇函数也是偶函数的性质，在判断加减复合的过程中，将“杂项”变换为常数0，消除它的影响．

三、 复合函数的奇偶性

对于复合函数的奇偶性，也可以用复合法则进行判断．

设函数y=f(t)与t=g(x)分别为复合函数y=f[g(x)]的外层函数(简称外函数)和内层函数(简称内函数)，则y=f[g(x)]的奇偶性如表1所示.

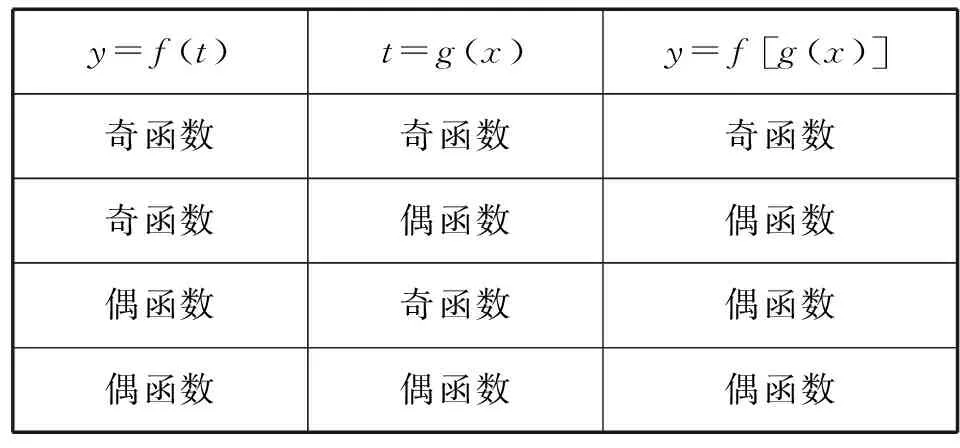
表1

由奇函数和偶函数的性质，可知奇函数中自变量带有负号可以向外提出，而偶函数自变量中的负号不能向外提出，即可内消．

因此，可以归纳出判断复合函数奇偶性的方法.首先，判断定义域是否关于原点对称；其次，不论是几层复合函数，一旦有一层为偶函数，则复合函数为偶函数，否则为奇函数．

例7判断下列函数的奇偶性．

(1)f(x)=sin(x3-x)；(2)g(x)=cos(x3+x)；(3)h(x)=|tanx|．

这种方法方便学生在审题时确定函数的奇偶性，但在处理具体问题时，一定要确认其定义域关于原点的对称性．

四、 函数的局部奇偶性

对于奇(偶)函数平移后得到的新函数，在此将其称为具有局部奇偶性函数，常用分离方法处理这类问题．

例8设函数f(x)=asinx-bx3+1，且f(3)=5，求f(-3)的值．

分析：对于函数f(x)=asinx-bx3+1，其中asinx-bx3为奇函数，y=f(x)的图像可由g(x)=asinx-bx3的图像向上平移1个单位得到．要求f(-3)，关键要求出g(-3)的值，而g(-3)=-g(3)．显然，g(3)=f(3)-1．

解：设g(x)=asinx-bx3，则f(x)=g(x)+1，所以f(3)=g(3)+1=5．

从而，g(3)=4，g(-3)=-g(3)=-4，则f(-3)=g(-3)+1=-3．

综上可知，要熟练掌握函数的奇偶性，不但要深刻理解奇偶性的定义，而且要能领会奇偶函数的本质特征．