垂直管气液两相流中压力降Orkiszewski预测模型的改进

董勇，罗雅琴，罗威，廖锐全，李梦霞

1.长江大学信息与数学学院，湖北 荆州 434023 2.气举试验基地多相流研究室(长江大学)，湖北 武汉 430100 3.长江大学石油工程学院，湖北 武汉 430100 4.长江大学计算机科学学院，湖北 荆州 434023

多相管流压力梯度的有效预测是油气井设计和分析的重要理论基础，一直是多相流研究的重点之一[1-4]。Orkiszewski模型是代表性的基于流型划分的垂直管多相流压力梯度预测模型，该模型是针对多个模型进行优选组合得到的。Orkiszewski对实际148口井测试数据的计算表明，其平均误差为-0.8%[5]，该模型得到了广泛的应用[6-13]。近年来，AKINSETE等[6]指出Orkiszewski模型是十分流行的模型，应用广泛；DANIEL等[7]指出Orkiszewski模型尤其适用于气液比波动范围大的情况，例如气举过程；FAHAD等[8]指出Orkiszewski模型仍然是重要且被广泛接受的压力降预测公式；KIRILL等[9,10]将Orkiszewski模型作为其求解算法的一部分；LUO等[11]、CHAARI等[12]指出Orkiszewski模型中含有大量参数，建议不要超过使用范围。总之，Orkiszewski模型是得到广泛认可的常用压力降预测模型。前述文献，或者直接使用模型，或者指出该模型具有一定的预测误差，没有量化考虑Orkiszewski模型的预测误差。PAULO等[13]基于实验数据对多种预测模型的预测误差进行了对比，表明Orkiszewski模型在部分数据上的预测相对误差超过了50%。笔者基于实验测试数据的计算结果也表明，Orkiszewski模型预测的压力梯度与实测压力梯度的平均相对误差为63.62%，对于油相连续的段塞流型，其平均相对误差达到76.17%。因此，有必要进一步研究Orkiszewski模型，提高压力梯度的预测精度。首先给出了实验数据的获取过程，对Orkiszewski模型进行了参数敏感性分析，指出液体分布系数模型中的阈值是最敏感的参数。同时分析了Orkiszewski模型的组成结构，提出了一种新的液体分布系数计算方法，得到了一种新模型。

1 实验数据获取

实验数据来自于多相流实验平台，平台设备的组成如图1所示。垂直管内径 75mm，液流量 10、15、20、30、40、50m3/d(含水率 0%)，气液比 50、100、150、200、300m3/m3，测试温度 27～29℃，介质是空气、5#白油，试验组数 30 组，粗糙度取 0.0002mm。

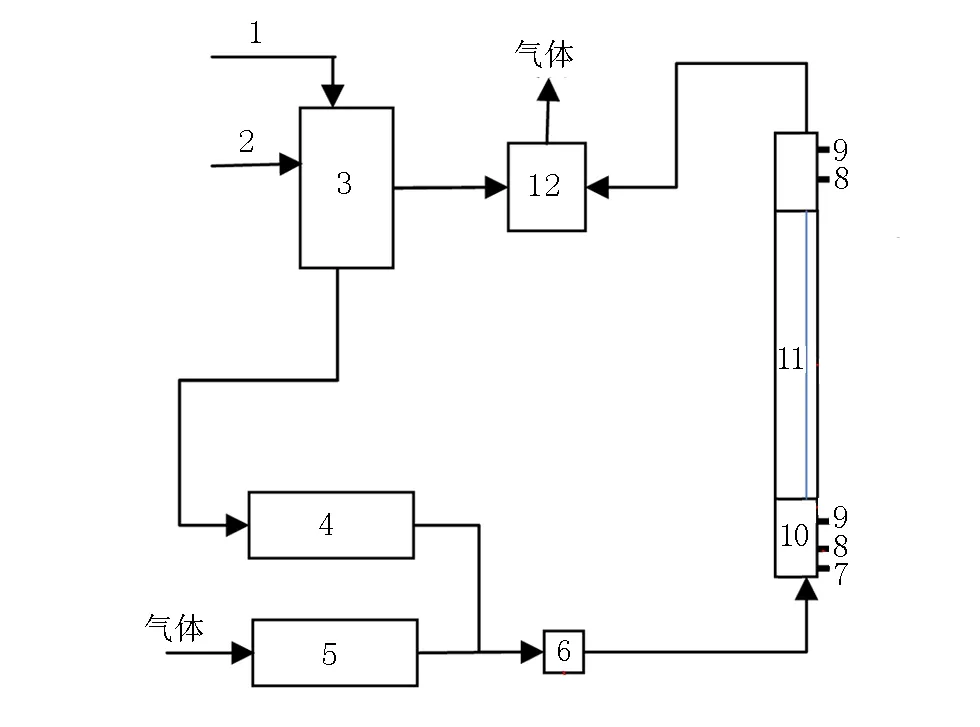
注：1-油入口，2-水入口，3-油水混合箱，4-液油水稳流系统，5-气稳流系统，6-气液混合器，7-排泄管，8-快速关断阀，9-传感器，10-不锈钢筒部分，11-玻璃钢筒观察段，12-气液分离器。图1 系统结构图Fig.1 System structure diagram

实验时首先按照实验设计方案，控制气流量和液流量尽可能接近设计值，待系统运行较为平稳时，记录流型(肉眼识别)，关闭快速关断阀，将管道放平，静置直到油气界面稳定，从玻璃钢筒观察段记录液相高度，换算出含水率数据。从监测仪器记录文件中提取流量、压力等参数。 所记录的数据包括：液流量、含水率、气流量、温度、压力差、流型。

2.Orkiszewski模型分析

Orkiszewski模型预测压力梯度[5,14,15]，其流程如图2所示。

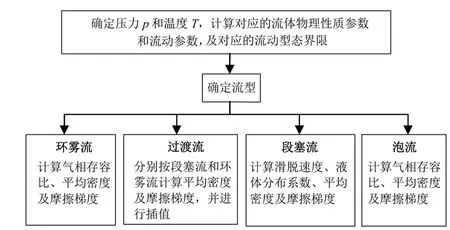
图2 Orkiszewski模型预测流程Fig.2 The prediction process of Orkiszewski model

根据流型规则，按流型将数据分类，如图3所示，实验中未出现泡流流型，出现了段塞流、过渡流、环雾流3种流型；图3中对角线上的点对应的预测压力降与实测压力降相等，数据点越接近对角线，预测误差越小。显然，环雾流流型对应的数据点分布在对角线附近，表明压力降预测误差较小，而段塞流流型和过渡流流型对应的压力降预测误差偏大。过渡流流型的压力降预测模型是由段塞流流型的预测模型和环雾流流型的预测模型加权平均得到的。因此，提高段塞流流型的压力降预测精度十分关键，需要进行参数的敏感性分析。

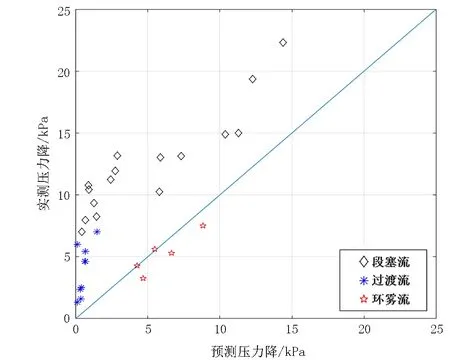
图3 实测压力降与预测压力降的对比Fig.3 Comparison between measured pressure drop andpredicted pressure drop

2.1 参数敏感性分析

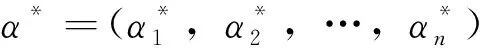
单因素敏感性分析的前提是建立系统模型，即确定输出Sout与影响因素α=(α1,α2,…,αn)之间的关联关系Sout=F(α1,α2,…,αn)，这种关联关系应尽可能写出具体的函数表达式。对部分复杂系统，也可以用有限体积法、函数拟合法等数值方法建立模型。有些系统甚至于只有一个离散数据集来反映系统输出和影响因素间的关联，建立的模型与实际系统符合度越高，则参数敏感性分析越有效。

基于系统模型，需要确定参考态对应的参数值(称为基准参数值)，而基准参数是依赖于问题本身的。例如要分析多相流压力降预测模型中液相黏度参数的敏感性，则黏度的实测值或常用黏度预测公式的计算值都可以取为基准参数值。基准参数值选定后，就可以进行参数的敏感性分析。在分析第k个参数对的范围内变化，系统输出Sout可以看作是关于参数αk的一元函数:

(1)

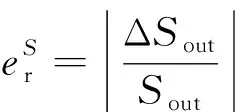
(2)

当Sk为影响因素αk变化1%时，系统输出Sout相应变化的百分比。

若Sout=f(αk)关于αk可导，令Δαk趋于0，由式(2)可得：

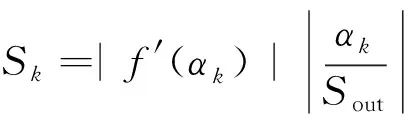
(3)

对所有的Sk(其中k=1，2，…，n)，Sk的值越大，系统输出Sout对因素αk越敏感。根据Sk的值，对比系统对各个因素的敏感性强弱，可以确定出重要因素。

定义相对误差：

(4)

式中：mv为测量值；pv为预测值。

实验数据点的相对误差的平均值就是平均相对误差，记为Mer。

(5)

式中：eri为第i个数据点的相对误差；N为数据点的总数目。

表2 敏感性分析结果Table 2 Sensitivity analysis results

从表2可知，Orkiszewski模型对阈值t2最为敏感，对油相相对密度γo也较为敏感，而对空气密度和液相黏度的敏感性较弱。敏感性分析结果表明，针对实验数据而言，阈值t2是最重要的参数，需要重点分析Mer关于t2的敏感性系数，Mer的变化方向表明可以尝试通过减小阈值t2来减小平均相对误差，如图4所示。在阈值t2减少15%时敏感系数曲线的取值达到最大，超过160%，在图示范围内敏感系数取值在70%以上，这表明了阈值t2的重要性。从平均相对误差曲线可以看出，当阈值t2减少50%时，平均相对误差达到最小，为39.48%。

图4 敏感系数曲线与平均相对误差曲线 Fig.4 Sensitivity coefficient curve and mean relative error curve

阈值因素出现在液体分布系数的计算过程中，而液体分布系数是段塞流流型压力降预测模型的一个参数。实际上段塞流流型压力降预测模型中，液体分布系数的计算过程最为复杂，其计算过程如图5所示。

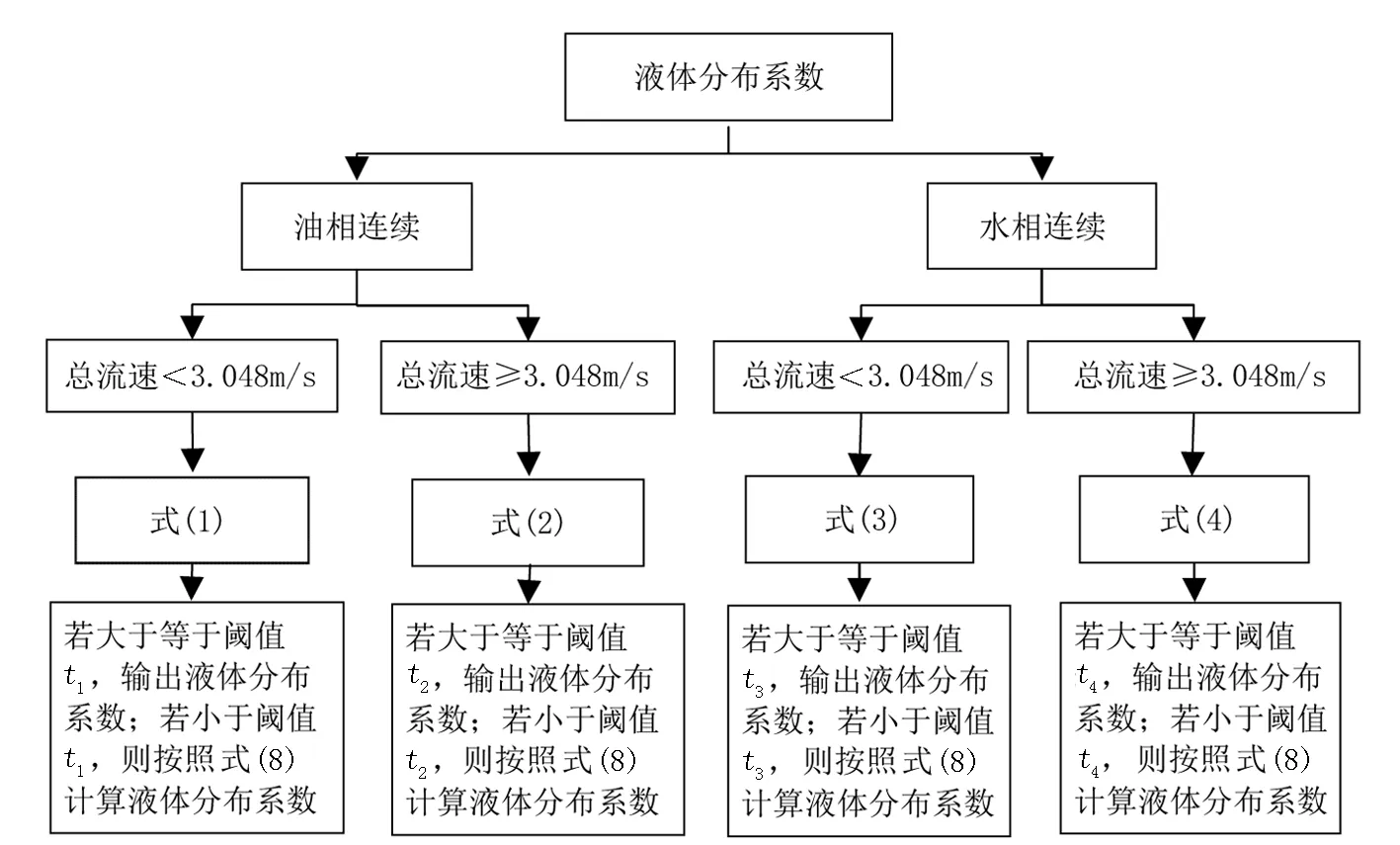
图5 液体分布系数计算流程Fig.5 Calculation process of liquid distribution coefficient

计算过程的复杂性表明了液体分布系数的重要性。因此，可以尝试从液体分布系数的角度改进预测模型。

文献[5]中对Orkiszewski模型预测效果的评价指标是平均预测误差，既不是预测平均绝对误差，也不是预测的平均相对误差，这实际上意味着该模型的预测误差可能较大，实际上文献[13]的结果也表明了这一点，如图6(根据文献[13]中图10修改得到)所示。

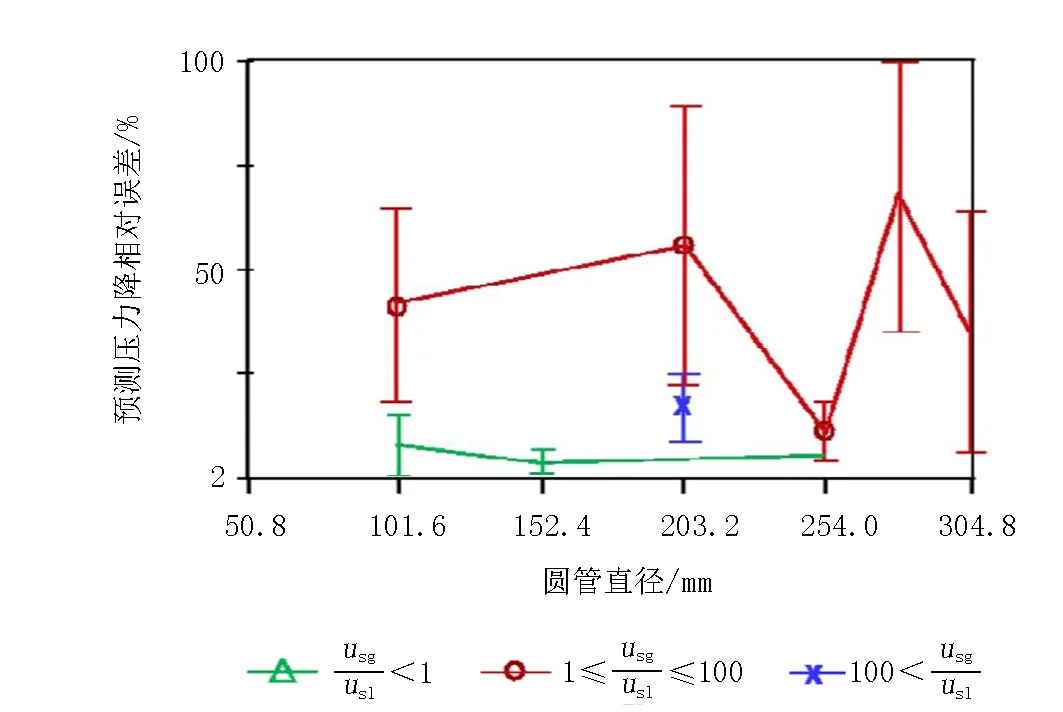
注：usg是表观气速，m/s；usl是表观液速，m/s。 图6 表观气速与表观液速不同比值范围内相对误差的平均值及标准差Fig.6 Mean and standard deviation of relative errors indifferent ratios of apparent gas velocity andapparent liquid velocity

当表观气速与表观液速的比值小于1时(绿色数据点)，在不同管径下Orkiszewski模型预测相对误差的平均值在10%以内，标准差小于5%；当表观气速与表观液速的比值大于100时(蓝色数据点)，Orkiszewski模型预测相对误差的平均值约为15%，标准差小于5%；当表观气速与表观液速的比值介于1和100之间时，Orkiszewski模型预测相对误差的平均值随管径的变化波动很大，低至约12%，最高超过70%，相应的标准差超过25%。

一方面，实验数据对应的管径是75mm，表观气速与表观液速的比值大于1，Orkiszewski模型的平均相对预测误差为63.26%，与图6中数据的分布规律具有一致性。另一方面，30个实验数据中，有1个数据点将观测的段塞流识别为过渡流，有3个数据点将观测的过渡流识别为环雾流，其余26个数据点肉眼观测的流型和算法识别的流型是一致的，符合比率高达86.67%。表明 Orkiszewski采用的流型界限[18,19]的可信度较高，模型预测误差的主要原因不在于流型界限不准。观察图3中不同数据点的整体分布规律，Orkiszewski模型对段塞流流型及过渡流流型的预测值整体偏大，表明对Orkiszewski模型的改进方向应该放在算法的段塞流流型及过渡流流型部分。综上所述，选取改进段塞流流型及过渡流流型中的液体分布系数是合适的。

3 液体分布系数的改进及验证

实验数据中，液相流体中含水率为0%，属于油相连续，对于Orkiszewski模型识别出的段塞流流型数据，容易计算出有12个点对应的总流速大于或等于3.048m/s。因此，本研究对Orkiszewski模型段塞流流型压力降预测模型的改进主要针对液体分布系数阈值t2。

Orkiszewski模型中，段塞流流型，油相连续、总流速大于或等于3.048m/s时，液体分布系数C0的计算公式如下：

C0=[0.00537×lg10(1000μl+1)]/D1.371+0.455+0.569×lg10D-(lg10vt+0.516)

{[0.0016×lg10(1000μl+1)]/D1.571+0.722+0.63lg10D}

(6)

式中：μl为液体黏度，Pa·s；D为管道内径，m；vt为气液混合物平均速度，m/s。

阈值t2如式(7)所示：

(7)

式中：vs为滑脱速度，m/s；A为管道截面积，m2；Q为总的体积流量，m3/s；ρm为两相流体混合密度，kg/m3；ρl为液相密度，kg/m3。

改进如下：

(8)

式中：k为系数。

图7展示了改进阈值后，不同k值对应的段塞流流型的预测压力降和平均相对误差，以及所有实验数据点对应的预测压力降和平均相对误差。

图7中，当k=1时，对应于原始的Orkiszewski模型。图7(a)、(c)、(e)中的数据点对应的总流速大于等于3.048m/s，且均为段塞流流型；当k=0.3时，新模型对预测压力降的改善最大，平均相对误差减小到17.21%，图7(e)相对于图7(a)平均相对误差下降了约59%。图7(b)、(d)、(f)为不同取值时，所有测试数据点新模型的预测效果对比图。当k=0.5时，平均相对预测误差最小，为34.98%，图7(f)相对于图7(b)平均相对误差下降了约29%。

图7(a)、(c)、(e)对应的最优值k=0.3，与图7(b)、(d)、(f)对应的最优值k=0.5不一致，原因在于过渡流流型下的Orkiszewski模型使用了段塞流流型的预测公式，针对段塞流流型改进的流体分布系数，会影响到过渡流流型的压力降预测。

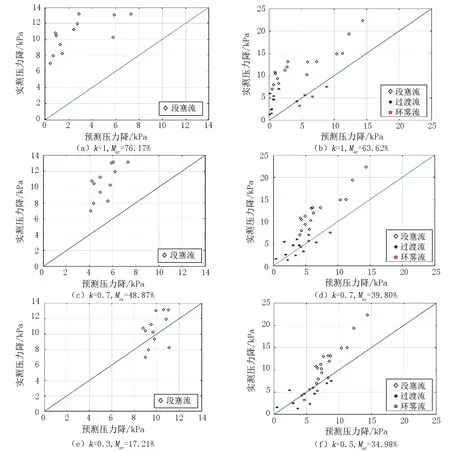
图7 不同的k值对应的预测效果图 Fig.7 Predicted results corresponding to different k values

4 液体分布系数的另一种改进方式

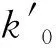
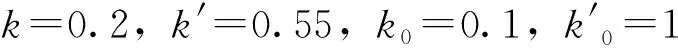
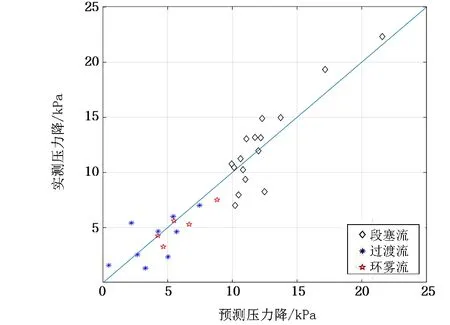
图8 多系数改进模型预测效果图(Mer=25.99%) Fig.8 Predicted results of multi-coefficient improved model(Mer=25.99%)

5 结论

1)针对垂直多相管流压力降预测问题，基于实验数据，采用敏感性系数的概念，分析了模型输出对影响因素的敏感性，指出的Orkiszewski模型中段塞流流型中液体分布系数的阈值是敏感性最大的因素。

2)针对实验数据的计算结果表明了模型改进方法的可行性，第一种改进模型的预测平均相对误差为34.98%，第二种改进模型的预测平均相对误差为25.99%，而原始模型的预测平均相对误差为63.62%。

3)限于实验数据仅含有油相连续情形，仅针对Orkiszewski模型中的油相连续部分，通过引入比例系数改进了液体分布系数阈值。若能获取水相连续的实验数据，可以对Orkiszewski模型中的水相连续部分进行类似改进，有望得到更高的压力降预测精度。