六自由度协作机器人绝对定位精度标定研究

冯利民，俞经虎*，王延玉，朱行飞，刘佳怡

(1.江南大学 机械工程学院，无锡 214122；2.江苏省食品先进制造装备技术重点实验室，无锡 214122；3.长广溪智能制造（无锡）有限公司，无锡 214000)

0 引言

机器人的定位精度是衡量机器人性能的重要指标。然而由于加工、装配等原因，机器人的绝对定位精度远低于某些应用要求，因此提升机器人的绝对定位精度已成为国内外机器人研究人员重点关注的问题[1]。机器人的绝对定位精度主要受几何因素与非几何因素的影响，其中几何因素主要包括装配误差、制造误差、磨损等，其引起的误差占对总误差的80%[2]。因此在提高机器人定位精度研究中，大多数研究者主要研究几何因素，对机器人运动学参数进行精确标定。

目前运动学参数标定方法一般分为四步：误差建模、误差测量、参数辨识和误差补偿[3]。对于机器人运动学参数标定，通常重点在于误差建模与参数辨识。文献[4]建立了基于微分变换的误差模型，并将其运用到运动学参数标定；文献[5，6]对工业机器人建立了完整的串联机器人微分误差模型，通过最小二乘法进行辨识，试验验证了误差模型的有效性；文献[7]运用Lavenberg-Marquardt算法对最小二乘法进行改进，有效提升了工业机器人的定位精度。上述文献表明，运用微分变换方法对误差建模、使用最小二乘法进行参数辨识能有效对机器人运动学参数进行标定。

本文为实现精确标定机器人运动学参数，简化标定过程，推导了基于微分变换的末端位姿线性误差模型，并且采用激光跟踪仪测量计算位置误差，并且将其代入该方程用于离线参数辨识，最后在Lavenberg-Marquardt算法改进的最小二乘法基础上，再次对Lavenberg-Marquardt算法进行改进求解参数误差，对机器人的运动学参数完成补偿修正。

1 机器人运动学模型

本文所研究的对象为长广溪智能制造公司新研发的六自由度协作机器人，其由六个旋转关节构成，各关节采用模块化设计，具有碰撞检测、拖动示教等功能，相对传统的工业机器人具有较好的安全性，可较好的实现人机协作功能。

首先采用DH法建立机器人运动学模型，其原理是通过建立机器人的连杆坐标系，得到各个关节之间的坐标关系，通过各坐标系变换矩阵相乘来描述机器人末端相对基座的位姿关系。根据DH参数建立规则与协作机器人的自身机械结构，可得到协作机器人的连杆坐标系（如图1所示）与DH参数表，如表1所示。

图1 协作机器人本体模型

表1 协作机器人DH参数表

图2 六自由度协作机器人连杆坐标系

运用机器人的正运动学可在已知机器人结构参数与各关节转角情况下，推导出机器人运动时关节i相对于关节i-1的理论位置与姿态，此时可得到关节i与关节i-1之间的转换矩阵T：

式(1)中，c为cos的缩写形式，s为sin的缩写形式。

2 运动学误差模型

2.1 单连杆误差模型的建立

由式(1)可知，当连杆参数ai-1、αi-1、di、θi存在一定误差，且误差足够小时可用微分方程表示误差方程，此时单个连杆运动产生dTi的变量误差，连杆坐标系由理论位姿Ti变为Ti+dTi，根据微分变换[8]，dTi与各连杆参数间的线性关系式为：

式(3)中，Δai、Δαi、Δdi、Δθi分别为连杆长度ai、连杆扭角αi、连杆偏置di、关节转角θi的误差量。

2.2 多连杆运动学误差模型的建立

当机器人有n个自由度时，结合上述单连杆的误差方程，将机器人多个连杆的微分变换的误差方程联立分析。设机器人末端相对于基座标系的位姿变换矩阵为TN，其误差矩阵为dTN，则此时实际位姿可由式(7)所示：

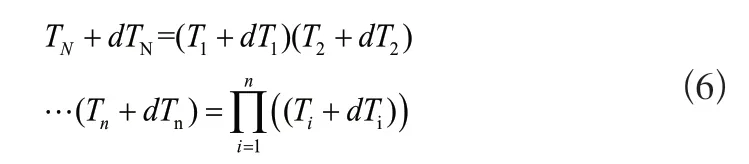
当误差量较小时，二阶以上微分误差项忽略不计[14]，此时可得到：

根据式(7)可得到：

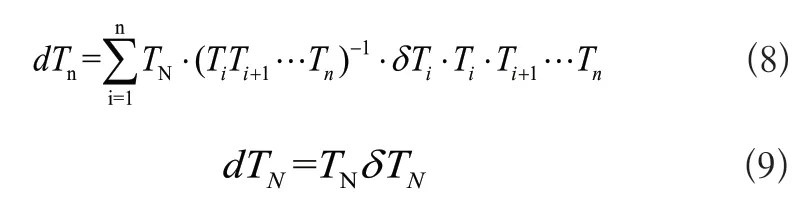
为简化式(8)，将机器人末端坐标系相对于关节i的转换矩阵用Ni表示：

将式(8)、式(9)、式(10)联立，此时可得到n自由度关节末端的误差矩阵模型：

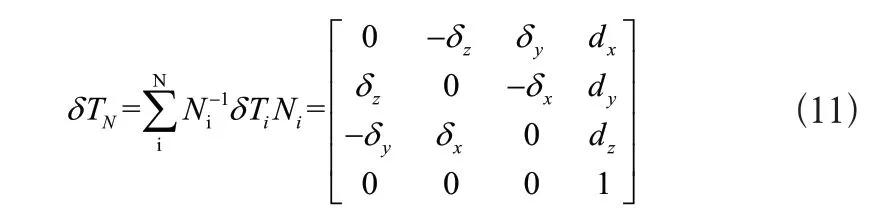
由式(11)可得到位姿误差一般形式[9]：

最终可将误差模型简化表示为：

最终，将机器人末端相对于基座的误差表示为待辨识的雅克比矩阵J与DH的参数误差矩阵u的乘积。本文研究对象为6自由度协作型机器人，测量关节角组数为30组时，在式(12)中，Δe是一个180×1的矩阵，表示理论位姿与实际位姿的差值；J是一个180×24的矩阵，表示基于误差的雅克比矩阵；u是一个24×1的矩阵，表示DH参数误差。

2.3 参数辨识

在建立机器人末端相对于基座坐标系的误差模型后，需要对模型求解得到DH参数误差。由于DH模型有4个参数，即对于n连杆串联机器人有4n个运动学参数，一组误差参数有着6个参数dx、dy、dz、δx、δy、δz，只能列出6个方程，若要解出所有参数，则需要取大于4n/6的整数组数据。对试验得到的多组数据处理，可得到一个超定的线性方程组。求解DH参数误差时通常采用最小二乘法，然而当雅克比矩阵的列之间存在线性关系时，采用普通的最小二乘法求解会出现奇异现象，进而影响计算结果，因此常见的解决办法采用式(13)所示的Lavenberg-Marquardt算法对最小二乘法进行改进[10]，其求解方程为：

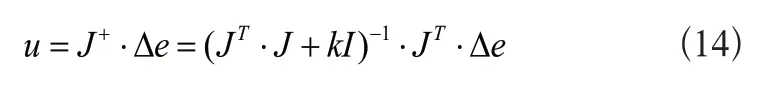
式(14)中，I表示单位矩；k表示组合系数，初值为0.01。

本文考虑到迭代的收敛速度以及参数辨识精度，将组合系数k与迭代前后位姿误差相结合，提升其辨识精度，在Lavenberg-Marquardt算法（L-MA）的基础上，再次对辨识算法进行改进，其组合系数如式(15)所示：

式(15)中，v表示调节因子，本文取10；Δei与Δei+1分别表示迭代第i次与第i+1次的平均位置误差。

将组合系数代入式(14)，最终得到改进的迭代L-MA辨识算法的求解公式：

当标定后的位置误差满足本次标定机器人精度要求时，迭代停止，输出此次辨识的运动学参数误差。标定过程流程如图3所示。

图3 标定算法流程图

3 机器人标定试验与分析

3.1 仿真分析

为验证本文的线性误差模型，首先预设一组较小的运动学参数误差如表2所示，设置机器人空间可变姿态范围内的30组关节角，用MATLAB仿真分析计算得到实际的机器人末端位置与理论位置，进而得到标定前的位置误差，将其代入式(13)求解运动学误差参数；再次将计算后的运动学误差参数代入运动学方程求解标定后的修正位姿，与其理论位姿进行比较分析。

表2 运动学参数误差预设值

本文中位置误差标定前后的位置误差由式(16)计算得到：

式(17)中，xr、yr、zr表示机器人末端实际的位置，xn、yn、zn表示机器人末端理论的位置；

经过计算，得到仿真条件下标定前后的定位误差，其结果如图4所示。应用本文建立的辨识算法，标定后的平均误差降低了0.250mm，较标定前降低43.2%；标定后的最大误差降低了0.604mm，较标定前降低60.3%；标定后的RMS误差降低了0.28mm，较标定前降低44.9%。相比普通的L-MA算法，标定后精度提升更加显著。该仿真试验表明本文建立的误差模型与辨识算法相对相比普通的标定效果更好，下文将通过试验进行验证分析。

图4 仿真标定前后位置误差

3.2 标定试验分析

仿真试验验证了本文误差模型与辨识算法的有效性，标定现场试验采用本文的误差模型与辨识算法进行验证。本文标定试验的测量系统为T-Mac装置与Leica AT960激光跟踪仪，试验测量系统如图4所示。此测量系统测量范围广，位置测量精度达到15um±6um/m，具有精度高、操作简便、实时性高等优点。

图5 标定试验现场

标定试验流程可简单概括为：

1）综合考虑机器人结构与激光跟踪仪工作范围，随机选择机器人可变姿态范围内30组关节角；

2）利用激光跟踪仪测量机械臂工具末端相对于激光跟踪仪的位姿及工具相对于机械臂六轴末端的对应关系；

3）采用正运动学方程求出30组关节角下末端工具相对于基座坐标系理论位姿与实际位姿的差值Δe，代入误差模型求解出DH参数误差；

4）将修正的DH参数写入控制器中，并取30组不同关节角进行精度验证分析。

对试验测量的位姿误差进行求解计算，并基于上文建立的误差模型，采用改进L-MA参数辨识算法，并对标定试验测得的参数误差进行辨识计算，最终其辨识结果如表4所示。

表3 DH参数误差

将表中的DH运动学参数误差补偿进控制器，并对关节零位角进行补偿，重新选取30组不同的关节角进行验证分析，得到标定前后的末端位姿，采用式(24)计算位置误差，通过计算得到标定前后30个末端位置误差如图6所示。

对标定前后位置误差进行处理，求得标定前后的位置与姿态的误差最大值，平均值，均方根值如表所示。由表5可知，六自由度协作机器人经过标定后，误差最大值，标准差值，均方根（RMS）值得到了显著降低，其中位置定位误差最大值减小了42.8%，位置定位误差平均值减小了61.9%，位置定位误差RMS值减小了59.3%，协作机器人定位精度得到了显著提升。

表5 标定前后位置误差

4 结语

本文以新研发的六自由度协作机器人为研究对象，采用微分法建立了协作机器人的误差模型，并采用改进的Lavenberg-Marquardt算法用于求解运动学误差方程。采用激光跟踪仪进行标定试验，试验结果表明，采用本文的辨识算法进行标定，位置定位误差最大值减小了42.8%，位置定位误差平均值减小了61.9%，位置定位误差RMS值减小了59.3%，绝对定位精度得到了有效提升，验证了本文提出标定方法的有效性。