抗落石冲击被动柔性防护网的设计选型
刘成清,张华鑫
(西南交通大学土木工程学院,四川 成都 610031)
落石灾害作为常见的自然灾害之一, 若不加以控制,可能会造成基础设施的损坏和人员伤亡。 柔性防护系统因其安全适用、布置灵活、经济美观、环境友好等优势而被广泛地应用于边坡落石灾害的防治[1-4]。柔性防护系统根据作用机理、适用范围、防治功能又分为主动柔性防系统和被动柔性防护系统。
目前,国内外的许多学者已经针对被动柔性防护系统及边坡稳定问题开展了大量的研究。 Hambleton 等[5]建立了用于确定金属柔性网临界能量的数值分析模型,并提出“子弹效应”的概念,即金属柔性网的临界能量随着落石尺寸的减小而减小的现象;Koo 等[6]研究了水平和垂直方向的被动柔性防护网在落石冲击作用下的动力响应,发现了欧洲规程ETAG27 中用于评估防护网系统的结构性能的布置方式并不一定是最不利工况;Albaba 等[7]提出了一种考虑干颗粒流影响的离散元模型,并对被动柔性防护系统在颗粒流作用下的动力响应进行了模拟分析;Tan 等[8]进行了被动柔性防护网的足尺冲击试验,对比分析了作用在柔性环网和支撑结构上的冲击力,并提出了一种用于估算落石冲击载荷的简便方法;Zhu 等[9]提出了一种用于模拟落石冲击被动柔性防护网的新型离散元模型, 通过与足尺试验数据的对比, 验证了该离散元模型的准确性和有效性;Mentani 等[10]提出了一种利用壳单元建立等效连续体模型的方法来模拟金属柔性网在落石冲击下的动力响应,为被动柔性防护系统的建模提供了参考;汪敏等[11-12]推导了单个ROCCO 圆环的等效半径计算公式和能量耗散计算公式,研究了不同组合形式、不同约束条件下的环形网受落石冲击作用时的耗能性能, 为环形网耗能性能的评价及工程应用提供了理论依据;崔廉明等[13]研究了环形网在不同直径落石冲击作用下的耗能性能;刘成清等[14]考虑了不同连接方式对于被动防护网各构件受力性能的影响, 并通过数值模拟研究了不同连接方式下被动防护网中各构件的受力情况,为提高被动柔性防护网的防护能级,建议在工程中优先采用钢柱与钢丝绳网两点连接、钢柱与基础间铰接连接的方式;孙波等[15]对落石冲击被动防护系统时的能量衰减规律进行了数值模拟分析;丁心香等[16]提出了一种用于求解边坡下限解的理论计算方法,通过与有限元解比较,验证了该方法的准确性。
综上所述,目前大多研究主要针对被动柔性防护结构的力学性能和耗能性能进行,而对其变形性能的研究相对较少, 尤其是以 “落石缓冲距离”和“残余拦截高度” 为被动防护结构变形性能的重要指标的相关研究更是鲜有见闻。 “容许缓冲距离”和“残余拦截高度”的示意图,如图1 所示。
图1(a)为落石缓冲距离立面图;图1(b),图1(c),图1(d)分别表示无支撑,单支撑以及双支撑环形网的残余拦截高度平面图。 L 和B 分别为长方形环形网模型的长度及宽度,m。虚线部分为落石冲击区域内环形网四周支撑绳偏离原始位置的变形图。
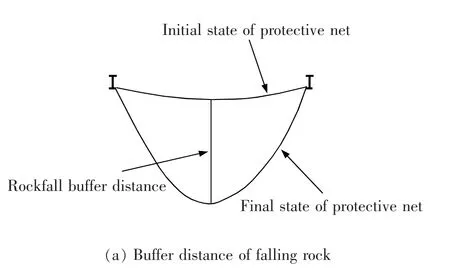

图1 缓冲距离与残余拦截高度示意图Fig.1 Buffer distance and residual intercept height
“落石缓冲距离”指标直接反应了被防护对象与被动柔性防护系统之间的距离,可以为工程设计和产品选型提供一定的参考依据。 同时,该指标也限制了被动防护结构的变形不宜过大,减少“落石虽拦截成功却对被防护对象造成损害”的风险;“残余拦截高度” 是指金属柔性网遭受落石冲击后,未移去所拦截落石前冲击断面内上下支撑绳间顺钢柱方向的距离。 本文提出一种通过增加竖向支撑改变被动防护结构变形性能的新型环形网,采用ANSYS/LS-DYNA 对其耗能性能及变形性能展开研究,以期为被动柔性防护系统的设计选型提供一定的参考依据。
1 被动柔性防护系统的组成及工作原理
被动柔性防护系统主要由钢柱、耗能器(此处为减压环)、支撑绳、拉锚绳以及金属丝网等构件按照 《铁路沿线斜坡柔性安全防护网》(TB/T 3089—2004)提出的安装方法组合而成,如图2 所示,图2(a)为安装在边坡上的被动柔性防护系统的组成剖面图,图2(b)从上至下分别是该系统对应的平面图以及立面图,通过对落石等运动物体的拦截将其限定在预定的保护区域外以达到对构筑物的保护和保障道路交通安全的目的。

图2 被动柔性防护系统的组成Fig.2 Composition of passive flexible protection system
金属丝网和减压环是整个系统的主要耗能构件和系统柔性的主要来源。 当受到落石冲击时,首先金属丝网通过自身材料的弹塑性变形耗散了落石的大部分冲击能量,少部分落石的动能则通过钢柱和拉锚绳传递至基础;但是,当被动柔性防护系统受到的落石冲击动能较大时(达到减压环启动时的阈值),由钢丝绳、铝套筒和钢管组成的减压环通过摩擦耗能和变形耗能继续耗散落石的能量[17],起到过载保护的作用, 降低了金属丝网被落石击穿的风险。 钢柱、支撑绳、拉锚绳等构件主要起到支撑和锚固作用。
2 有限元分析模型与假设
2.1 有限元模型
选取工程中常用的长方形环形网模型,模型的尺寸:长度L 为10 m,宽度B 为5 m。为改善环形网的变形性能,本文提出了一种增加竖向支撑的方案。 同时,为了更好地与传统形式的环形网进行比较分析,分别建立了无支撑,单支撑,双支撑3 种形式的环形网模型平面图,如图3 所示。

图3 3 种形式的环形网Fig.3 Three forms of ring net
选取了2 种工况以及具有代表性的落石冲击位置进行数值模拟,从环形网的耗能性能和变形性能对这3 种模型进行比较分析。 耗能性能指标选取为环形网在当前工况下的最大耗能;变形性能指标通过环形网的“残余拦截高度”以及“落石缓冲距离”反映。 2 种工况分别是:工况1 为其中一种模型率先达到临界破坏状态(此时对应于落石的极限速度),而另外两种模型未达到临界破坏,取达到临界破坏状态下的环形网模型所对应的落石临界速度作为模拟落石冲击这3 种环形网模型过程中的共同速度;工况2 为3 种模型均达到各自的临界破坏状态,取此时3 种环形网模型对应的落石临界速度分别作为模拟落石冲击这3 种模型过程中的极限速度。 代表性的落石冲击位置的有4 个:落石冲击位置1 为双支撑环形网模型Ⅰ区的几何中心;落石冲击位置2 为单支撑环形网Ⅰ区的几何中心;位置3 为双支撑环形网左侧竖向支撑的几何中心; 位置4 为环形网的几何中心。 4 个典型的落石冲击位置的平面图如图4 所示,其中d 为落石冲击环形网时接触区域的中心与最左侧支撑绳之间的距离,m;阴影区域代表落石;Ⅰ、Ⅱ、Ⅲ代表增加竖向支撑后长方形环形网被划分成的子环形网。
2.2 单元选取与材料参数
采用ANSYS/LS-DYNA 软件对落石冲击环形网的过程进行数值模拟, 分析中所选取的单元:环形网和卡扣均采用Beam161 单元,主要考虑其在拉伸变形过程中还需承受一定的弯矩; 支撑绳采用Link160 单元,该模型只考虑构件受到轴力作用,不能承受弯矩作用;选用Solid164 单元对落石进行模拟。 分析时间取为0.3 s。 落石与环形网采用自动梁面接触,支撑绳、环形网与卡扣之间采用通用自接触,以此考虑不同材料模型之间计算的协调性。
各种材料的力学性能指标见表1 所示。 在数值模拟时采用的材料模型: 落石采用刚性体模型,同时假定落石为球体,为减小“子弹效应”发生的概率,落石直径取为1.2 m;由于不考虑卡扣的破坏效应,卡扣采用线弹性模型;考虑到单元失效和破坏效应,环形网、支撑绳均采用塑性随动模型,通过Cowper-Symonds 模型来考虑材料的塑性应变效应。用与应变率有关的因数表示屈服应力

表1 材料力学性能指标Tab.1 The mechanical properties of the materials

式中:σy为考虑应变率影响的屈服应力,σ0为初始屈服应力,MPa;ε 和εpeff分别为应变和有效塑性应变;Ep为塑性硬化模量,GPa;β 为硬化参数,在0 到1 之间取值;C 和P 为应变参数,对于钢材可分别取C=40,P=5。
2.3 条件假定
由于环形网在落石冲击作用下的变形较大,能量转换关系较复杂,为简化计算模型,提出如下条件假设:
1) 在有限元建模时为简化计算和提高计算效率,落石冲击过程中仅考虑落石的平动速度,而忽略落石转动速度的影响, 且不考虑落石破碎的情况;
2) 落石缓冲距离是指落石从开始与环形网接触到速度降为0 这一过程中所运动的距离;
3) 落石极限速度的确定[11]:在数值计算中,假设落石速度为vlim时,模型未发生破坏,而当落石速度为(vlim+1)时,环形网发生破坏,vlim即为环形网发生临界破坏时对应的落石极限速度。
3 环形网在落石冲击作用下的变形性能对比分析
为提高环形网的残余拦截高度和减少落石缓冲距离,在保证环形网尺寸不变的情况下,通过增加竖向支撑的方式建立了无支撑、单支撑、双支撑3种形式的环形网模型, 设置2 种工况进行落石冲击作用下环形网的变形性能分析。
3.1 残余拦截高度
由图5 可见,2 种工况下的环形网模型的残余拦截高度随落石冲击位置的变化规律基本上一致,且在同一冲击位置时,双支撑环形模型的残余拦截高度均大于单支撑环形网模型,主要原因是双支撑环形网模型的整体刚度更大,在落石冲击作用下结构的变形有所减小。 然而在落石冲击位置时,单支撑环形网模型的残余高度比双支撑环形网更高,这是因为单支撑的布设位置恰好位于此处,导致该位置的约束作用加强,环形网的竖向变形减小。 在工况1 时,除落石冲击位置在时单支撑环形网模型率先达到临界破坏,其余冲击位置均为双支撑环形网模型先达到临界破坏。 这说明当落石冲击环形网中大多数位置时,在既保证环形网处于正常工作状态又可以提高其残余拦截高度的前提下,相比于无支撑环形网,单支撑环形网模型的性能优于双支撑环形网。

图5 2 种工况下不同环形网的残余高度Fig.5 Residual heights of different ring nets under two conditions
3.2 落石缓冲距离
图6 给出了2 种工况下不同环形网模型的落石缓冲距离。

图6 两种工况下不同环形网的落石缓冲距离Fig.6 Rockfall buffer distances of different ring nets under two conditions
由图6 可知,2 种工况下的落石缓冲距离随着冲击位置的变化规律基本上一致。 无支撑和单支撑环形网模型的落石缓冲距离随着冲击位置的变化总体上呈现出下降的趋势, 且在落石冲击位置时,落石缓冲距离最大,所以在科学研究中通常选取落石冲击环形网平面的几何中心为最不利工况;而在同一冲击位置时,双支撑环形网模型较单支撑环形网模型对于减小落石的缓冲距离效果更加明显,但随冲击位置的变化,落石缓冲距离变化较大并表现出明显的跳跃性(波动性),相比而言,单支撑环形网模型可以有效减小落石的缓冲距离且平稳性好。此外,在冲击位置时,单支撑环形网模型在减小落石缓冲距离方面的效果与双支撑环形网模型接近甚至更优。 综合考虑减小落石缓冲距离的效果及稳定性,建议在环形网设计选型时宜优先选用单支撑形式的环形网。
4 环形网在落石冲击作用下的耗能性能对比分析
由于增加支撑后的环形网结构的整体刚度增加,其依靠环形网变形所消耗的落石冲击能量必定会相应的降低,所以需要对环形网在落石冲击作用下的耗能性能进行研究。 2 种工况下不同环形网的最大耗能,如图7 所示。

图7 2 种工况下不同环形网的最大耗能Fig.7 Maximum energy consumptions of different ring nets under two conditions
首先,在工况1 时,为了描述瞬时冲击作用下环形网对于落石能量耗散的程度,引入“最大耗能占比”的概念,即在设定的数值模拟分析时间内环形网的最大耗能与落石初始冲击动能的比值


式中:m 为落石质量,kg;v 为当前工况下落石接触防护网时的线速度,m/s。
根据图7 可知,两种工况下不同环形网的最大耗能差异较大。 当工况1 时,除落石冲击位置d/L=1/2 外, 其余冲击位置的落石冲击动能的变化规律相似且单支撑和双支撑环形网的最大耗能相差不大, 但是均明显高于无支撑环形网的最大耗能,该结论也可以在图8 中得到验证;然而在d/L=1/4 处,3 种形式的环形网的耗能性能均最差; 在d/L=1/2处,由于3 种形式的环形网模型中对环形网平面几何中心位置的约束程度不同,使得该位置的最大耗能产生了显著的差异,其中单支撑环形网最大耗能较双支撑显著降低,这是因为当落石冲击环形平面几何中心位置时,单支撑环形网的竖向支撑首先消耗了一部分落石的能量,导致这一过程中冲击位置周围参与耗能的网环数目相对较少。 当工况2 时,带支撑(单支撑和双支撑)环形网的最大耗能较无支撑环形网的最大耗能有所降低,但双支撑环形网模型降低的幅度更为明显,尤其是当冲击位置d/L=1/4 时, 双支撑环形网的最大耗能接近是无支撑环形网最大耗能的一半(见表5)。
表2, 表3 分别给出了工况1 时落石的速度和工况2 时落石的极限速度,相应的冲击动能如表4、表5 所示。

表2 工况1 时落石的速度Tab.2 Velocity of falling rocks under condition 1m/s

表3 工况2 时落石的极限速度Tab.3 Limiting velocity of falling rocks under Condition 2 m/s
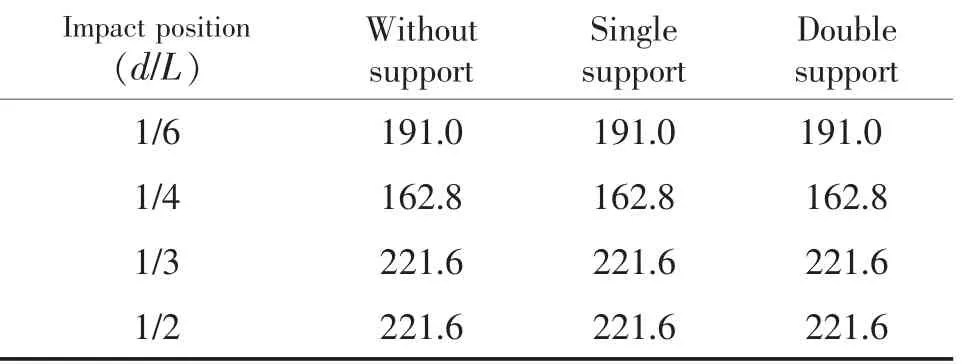
表4 工况1 时落石的冲击动能Tab.4 Impact kinetic energy of falling rocks under condition 1kJ

表5 工况2 时落石的极限冲击动能Tab.5 Limiting impact kinetic energy of falling rocks under condition 2kJ
由表2 可知,当其中一种环形网模型率先达到临界破坏状态(此时对应于落石的极限速度),而另外两种模型均未达到临界破坏时,大多数落石冲击位置均是双支撑环形网率先达到临界破坏状态,表明此形式的环形网承受落石冲击荷载的能力有限,工程应用存在一定的局限性。 表中*表示在当前冲击位置率先达到临界破坏时的环形网模型对应的落石极限速度。
从表3 中可以看出,3 种形式的环形网达到各自临界破坏状态时对应的落石极限速度随冲击位置的变化相差不大,在冲击位置d/L=1/2 时,落石的极限速度基本上大于其他冲击位置,说明科学研究中取环形网的几何中心作为落石冲击位置相对不安全;但是同一冲击位置,相比于无支撑环形网,带支撑环形网的落石极限速度均有不同程度的下降,但单支撑环形网降低的幅度更为明显,为方便应用于工程中,可通过适当增加网环的缠绕圈数以提高环形网的整体承载能力。
图8 给出了不同环形网的最大耗能占比P 随落石冲击位置d/L 的变化规律曲线。

图8 不同环形网的最大耗能占比Fig.8 Maximum energy consumption ratios of different ring nets
从图8 中可以看出,在瞬时(0.3 s)冲击作用下, 单支撑环形网和双支撑环形网在除d/L=1/2 位置外的其余冲击位置,两种形式的环形网的最大耗能占比均达到了90%以上并且相差不大,说明带支撑环形网具有迅速衰减落石能量的功能;相比于双支撑环形网,单支撑环形网的稳定性好,更适用于二次防护。当d/L=1/2 时,单支撑环形网的最大耗能占比明显低于双支撑环形网,主要原因是落石冲击该位置时,单支撑环形网的竖向支撑在为发生断裂前,主要承担了一部分落石的冲击能量,致使冲击位置附近参与耗能的网环数量较少,该处的耗能较低;而当竖向支撑发生断裂后,陆续有更多的网环参与耗能,最终单支撑环形网的最大耗能明显高于双支撑环形网(图7(b))。
综合以上对比分析可以看出,带支撑环形网可以有效地提高环形网的残余拦截高度并降低落石的缓冲距离;但是与无支撑环形网相比,带支撑环形网的最大耗能均有不同程度的下降,尤其是双支撑环形网的最大耗能下降幅度更为明显,主要原因是:增加竖向支撑后,单支撑和双支撑环形网结构存在一定的“尺寸效应”。 “尺寸效应”是指结构整体或局部尺寸的微小化引起结构性能变化的现象。 竖向支撑将长方形环形网划分成几个相同的子环形网区域(图3),当落石冲击其中一块子环形网区域时,致使带支撑环形网实际参与耗能的网环数量较无支撑环形网均有不同程度的减小,且双支撑环形网的减小幅度更为明显。 与此同时,带支撑环形网在瞬时冲击作用下的最大耗能占比很高,具有迅速衰减落石能量的功能。
与双支撑环形网相比,单支撑环形网具有如下优势:能有效的提高环形网的残余拦截高度,降低落石缓冲距离且稳定性好;最大耗能占比与双支撑环形网相近且工况2 时的最大耗能相对于无支撑环形网的下降幅度较小,可以通过适当增加网环的缠绕圈数以提高结构的最大耗能。 为降低“落石虽拦截成功但是却对被防护对象造成损害”的侵限风险,建议在防护网铺设位置距离道路较近的边坡或者陡峭边坡中的防护网水平铺设时,应优先选用单支撑环形网。
此外, 虽然落石冲击1/3 和1/2 位置竖向支撑绳断裂破坏,但是柔性防护网设计中考虑了在距离环形网下部一定距离的位置设置有负责用于拦截小直径落石的钢丝格栅网,因此断裂的钢丝绳不会对下部通行车辆的安全造成威胁。
5 结论
1) 带竖向支撑的环形网可以有效降低落石的缓冲距离并提高环形网的残余拦截高度,但环形网的最大耗能均有不同程度的下降,可以通过适当地增加网环的缠绕圈数弥补。
2) 当其中一种环形网模型率先达到临界破坏状态(此时对应于落石的极限速度),而另外两种环形网模型未发生破坏时, 除落石冲击位置在d/L=1/3 时单支撑环形网模型率先达到临界破坏, 其余冲击位置均为双支撑环形网模型先达到临界破坏。这说明当落石冲击环形网中大多数位置时,在既保证环形网处于正常工作状态又可以提高其残余拦截高度的前提下,相比于无支撑环形网,单支撑环形网模型的性能优于双支撑环形网; 与此同时,带支撑环形网的最大耗能占比均达到了90%以上,说明该结构在瞬时冲击作用下具有迅速衰减落石能量的功能且落石缓冲距离小;而与双支撑环形网相比,单支撑环形网的落石缓冲距离随冲击位置变化的平稳性好,适用于二次防护。
3) 对于需要考虑被动柔性防护系统变形距离的实际工程,如:防护网铺设位置距离道路较近的边坡或者陡峭边坡中的防护网水平铺设等落石防护工程,建议优先选用单支撑环形网。

