一种低输入纹波电流的反激变换器

袁义生，刘 伟，刘文钦，张执钦

（华东交通大学电气与自动化工程学院，江西 南昌 330013）

随着高速铁路的飞速发展，列车安全运行的问题日益突出， 铁路机车内部诸如辅助开关电源、模块电源等车载电子设备的可靠工作是列车可靠运行的技术保证[1-3]。 然而，随着开关电源高频化和小型化的发展趋势， 开关速度提高，PCB 布局更加紧凑，由开关变换器开关动作产生的固有纹波电流带来的电磁干扰问题愈发严重，引发降低电路瞬态响应、缩短输入源的寿命、削弱电能质量等诸多问题。

为了抑制固有纹波电流，采用电容滤波是成本最低、结构最简单的方法，但其使用寿命低及易老化的缺点容易导致系统故障[4]；因此可以结合电感组成LC 滤波器来避免该问题[5-6]，进而实现纹波电流的抑制， 但是串联在功率线上的LC 滤波器带来的损耗问题严重[7-8]。 目前抑制纹波电流主要措施分为有源方案和无源方案两种。

有源方案普遍采用有源控制电路结合小容量无源器件的结构，因具有体积小、便于集成的特点而得到应用[9-12]。 Lai 等[9]针对典型的单相boost PFC整流器输入电流纹波大的问题， 提出一种开关管和电容组合的有源电路，实现了输入侧的纹波电流的抑制，但其缺点是控制方法复杂、抑制效率低、系统的稳定性不高。 Mao 等[10]提出一种基于半桥电路的DC-DC 拓扑，通过构建有源纹波电流补偿支路并结合控制方式，有效地抑制了拓扑输出端的纹波电流，但该方法仅能处理连续纹波电流，且补偿支路要求和主电路对称，应用具有局限性。有源方案虽在开关电源高频小型化方面具有优势，但其弊病是电路成本高、损耗较大、系统稳定性差，难以在全负载范围内工作且仅适合工作在小功率范围。

无源方案是一种利用变压器、电感、电容等无源器件构造补偿支路，补偿纹波电流的方法，因具有结构简单、损耗小、易于模块化的特点而得到了广泛应用[13-15]。 Chen 等[13]针对反激变换器输入侧固有的断续纹波电流，采用耦合电感构造了纹波补偿电路，其优点是工作范围宽，但其纹波抑制效果易受磁性器件的耦合系数所制约，且补偿电路与主电路之间通过磁性器件相互影响， 降低了系统稳定性。 为此针对这些问题，以典型的反激变换器为例，提出了一种无源纹波补偿电路， 通过利用变压器、二极管、电解电容，构造了同样工作在反激状态下的补偿支路，产生了补偿电流，极大地补偿了主支路上的断续纹波电流。 且其具有易于集成和模块化、设计简单、损耗小、不受耦合系数的影响、与反激变换器的工作互不影响的优点。

1 拓扑结构及工作原理

1.1 拓扑结构

所提出的低输入纹波电流的反激变换器如图1所示，由无源纹波补偿电路和传统反激电路两部分组成。 其中，无源纹波补偿电路由电解电容C2、变压器T2、二极管D2、高频理想变压器T3、电解电容C3构成；反激电路由主变压器T1、开关管Q1、二极管D1、输 出 滤 波 电 容C1构 成；Lm1，Lk1，Lm2，Lk2分 别 为T1，T2的励磁电感与漏感。

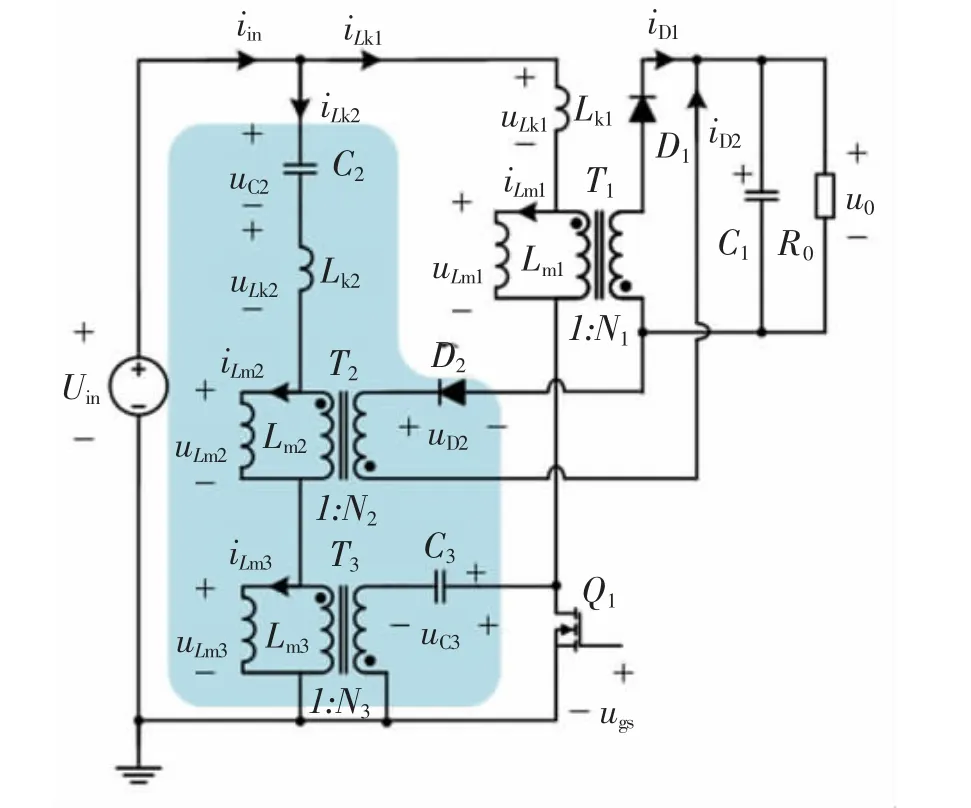
图1 提出的低输入纹波电流的反激变换器Fig.1 The proposed flyback converter with low input ripple current

1.2 工作原理

开关管Q1采用PWM 工作模式，变换器工作在连续模式， 一个开关周期内经历两个工作状态，主要工作波形如图2 所示。 由上到下依次为：驱动电压ugs；主变压器T1的励磁电感电压uLm1、流过漏感Lk1的电流iLk1、励磁电流iLm1；分别流过功率二极管D1，D2的电流iD1，iD2；变压器T2上的励磁电感上的电压uLm2、流过漏感Lk2的电流iLk2、励磁电流iLm2；输入电流iin。

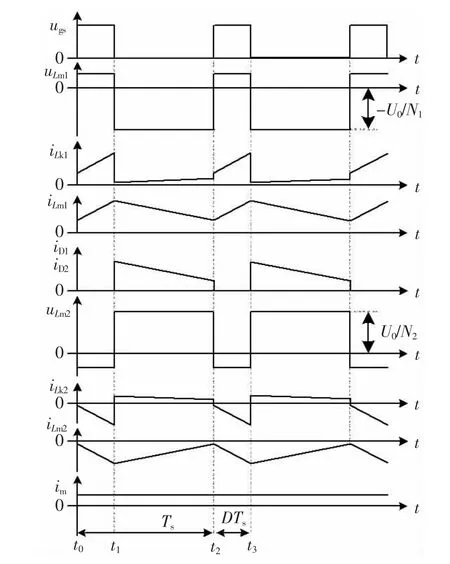
图2 主要波形Fig.2 Main waveforms

为简化分析，假设除变压器T1与T2外，其余均为理想器件， 开关管的开关状态转换时间为零，输出电压uo恒定为平均值Uo，C2与C3的电压恒为Uin，各变压器的漏感电流等效为各支路上的电流。

1.2.1 工作状态1[t0-t1] -Q1导通

变换器各个器件的工作状态如图3（a）所示，to时刻开关管Q1导通，二极管D1，D2关断。变压器T1，T2原边绕组储能，电容C1向负载Ro释放能量，此时励磁电 流iLm1，iLm2分 别 与 漏 感 电 流iLk1，iLk2相 等，主变压器T1的漏感电压uLk1表示为

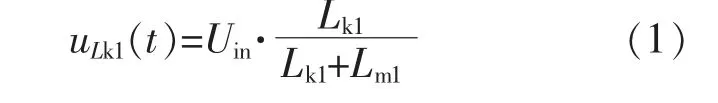
可知uLk1的值为正，变压器T1原边绕组电流iLk1正向线性增长，励磁电感Lm1储能增加。

与此同时， 电容C3给变压器T3的副边绕组充能，uLm3表示为uC3/N3，根据基尔霍夫电压定律，纹波补偿支路上变压器T2的漏感电压uLk2表示为

由于C2与C3的电压恒为Uin， 所以式中uLk2为负，结合变压器T3的原副边电流的关系，电流iLk2反向上升，对纹波电流iLk1进行补偿。

变压器T2的工作状态与主变压器T1类似， 励磁电感Lm2储存能量，可以得到二极管D2的端电压为uD2

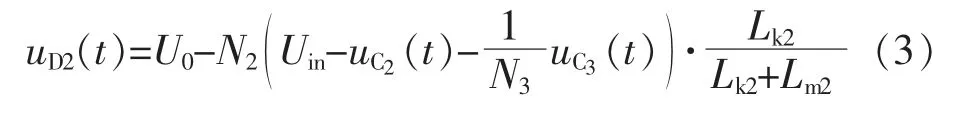
可知上式的值为正，此时二极管D2处于断态。

1.2.2 工作状态2 [t1-t2] -Q1关断

变换器各个器件的工作状态如图3（b）所示，t1时刻开关管Q1关断，二极管D1，D2导通。 储存在T1的励磁电感Lm1中的磁场能量经过二极管D1向负载Ro释放，励磁电感电压uLm1被箝位为-uo/N1，励磁电流iLm1正向线性下降。 同时，储存在T2的励磁电感Lm2中的磁场能量通过二极管D2向负载Ro释放，励磁电感电压uLm2被箝位为uo/N2，励磁电流iLm2反向线性下降。 与传统反激电路不同，由于电容C3的存在，当开关管Q1关断后，储存在漏感Lk1中的能量通过T3的副边绕组向电容C3释放， 开关管两端被电容C3和变压器T3副边电压所箝位。 该工作状态下漏感电压uLk1，uLk2可分别表示为

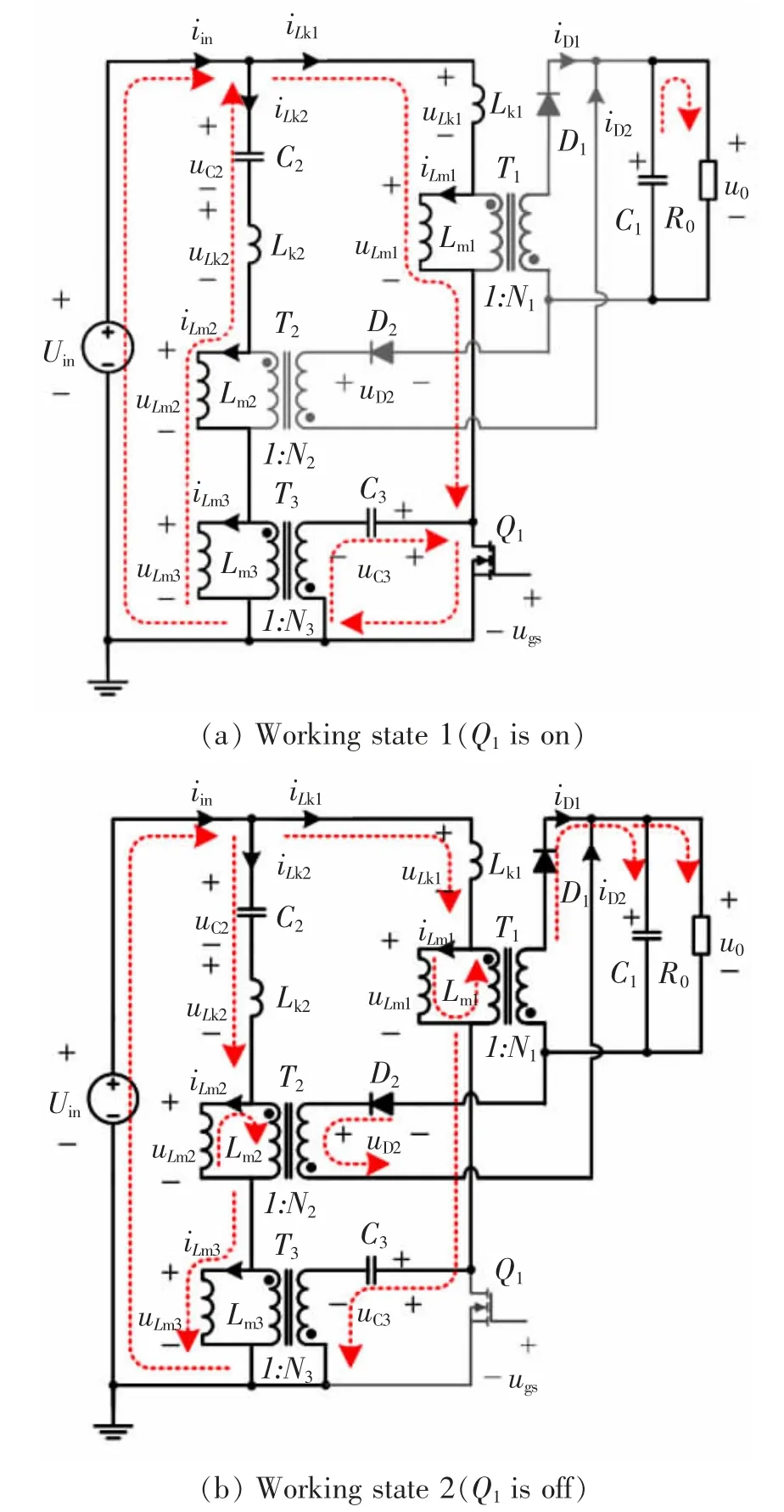
图3 两个工作状态Fig.3 Two working states

根据假设条件，可知此时uLk2为负，电流iLk2正向线性下降。而uLk1及iLk1的变化由各变压器的变比决定，将在波抑制条件推导中讨论。

2 增益分析

根据稳态下电感电压的周期平均值为零的原则，针对T1的励磁电感Lm1，有

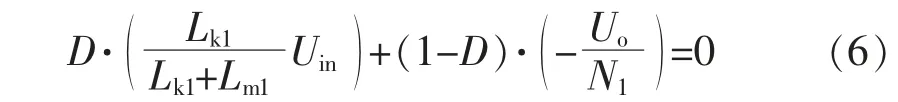
由于漏感Lk1很小，忽略不计，得到输入、输出电压关于开关占空比的表达式

可以看出其与传统反激变换器的电压增益一致，即证明无源纹波补偿电路与反激变换器的工作互不影响。

3 纹波电流抑制条件分析

参考图3（a），对工作状态1 下的变换器列出回路方程式

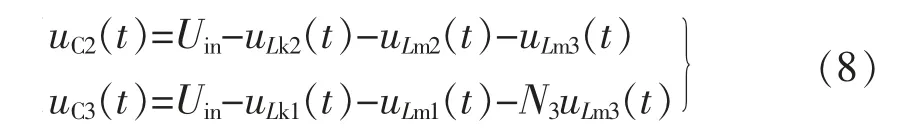
对上式左右两边同时取平均值，并根据电感伏秒平衡定理，化简得到

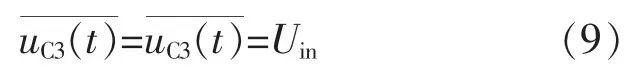
由于电容电压不能突变， 实际情况下变化很小，在时域分析时可采用平均电压Uin等效。

无源纹波补偿电路实现纹波电流抑制的最终目的是将传统反激变换器的输入电流iin补偿为恒定的直流，即要求其变化率为0，也即

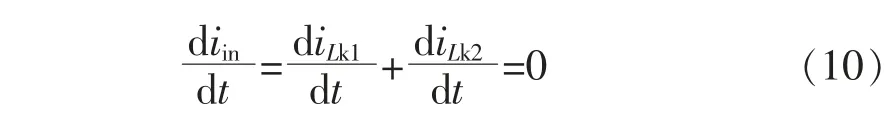
根据式（1）、式（2）、式（8），在工作状态1 下要求

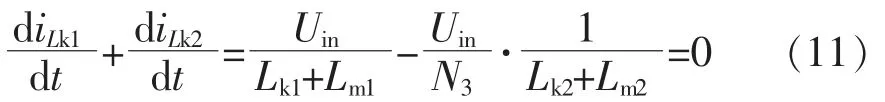
根据式（4）、式（5）、式（8），在工作状态2 下，要求加在漏感Lk1上的电压uLk1为正，使iLk1的变化率diLk1/dt 为正，以便实现电流iLk2的负变化率对iLk1的正变化率进行补偿，即要求

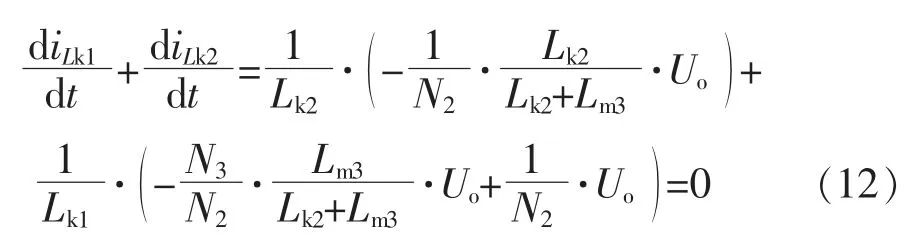
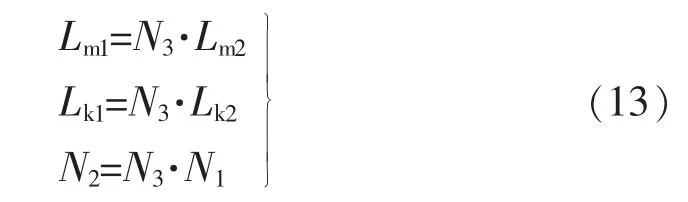
化简式（11）、式（12），得到无源纹波补偿电路的设计原则，也即纹波电流抑制的充要条件为

4 相关变量的参数计算

从图2 可看出，无源纹波补偿电路在反激变换器中的应用，改造了电流iLk1和iD1的波形，创造了电流iLk2和iD2， 它们对变压器和二极管的设计至关重要，需要进行计算。

图4 为变压器T1的原边绕组漏感电流iLk1及副边二极管电流iD1的直观图。 ILk1，on，ILk1，off分别表示电流iLk1在工作状态1（Ton）、工作状态2（Toff）内的平均值，ΔiLk1，on，ΔiLk1，off分别表示电流iLk1在Ton，Toff内的变化量，ID1，off，ΔiD1，off分别表示电流iD1在Toff内的平均值和变化量，t1,on，t1,off，t2，on，t2,off分别表示不同的时刻。td，on和td,off表示开关状态转换的时间，为方便下文计算，将其理想化为零。

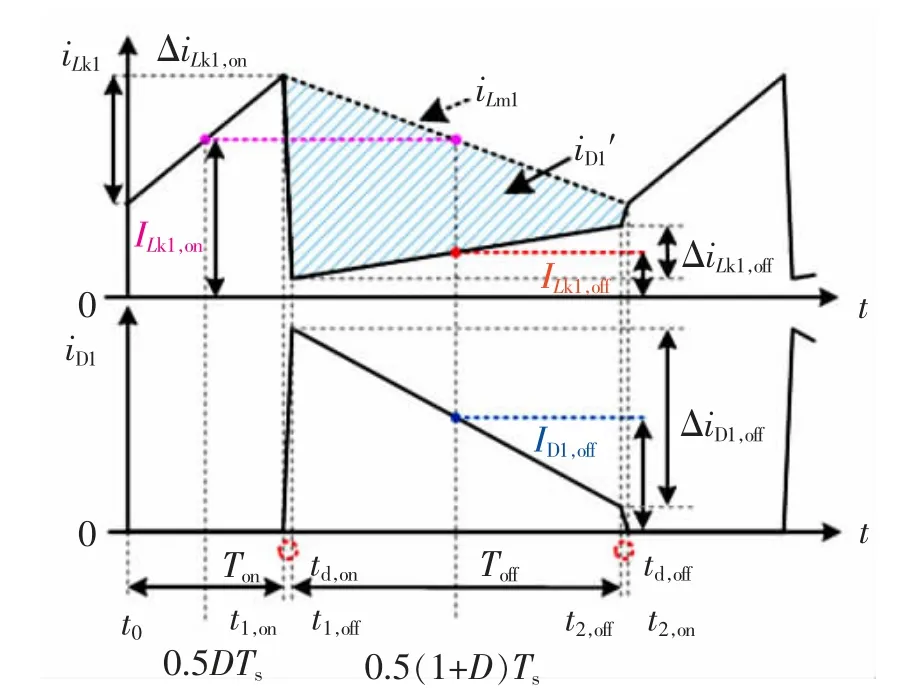
图4 变压器T1 相关电流的直观图Fig.4 Visual diagram of related current of transformer T1

图5 为变压器T1在Toff内的T 型等效电路，其中R1表示一次侧绕组的电阻，Rm表示铁耗等效电阻，R′，Lk′，iD1′分别表示二次侧绕组折算到一次侧的等效电阻、等效漏感以及等效电流。 此时，原边漏感电流iLk1与副边等效电流iD1′同时流经励磁电感Lm1，与图4 中阴影部分所描绘的iD1′一致，可列出关系式如下

图5 变压器T1 的T 型等效电路（Toff）Fig.5 T-type equivalent circuit diagram of transformer T1（Toff）

根据前节所述， 变压器T2工作在反激状态，在符合纹波电流抑制条件下， 可知在Toff内二极管电流iD1与iD2相等，结合图4、图5，针对二极管D1，有如下表达式

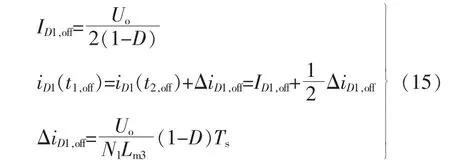
同理，针对Toff内的漏感Lk1，根据图4，结合式（4）、式（7）、式（13），有

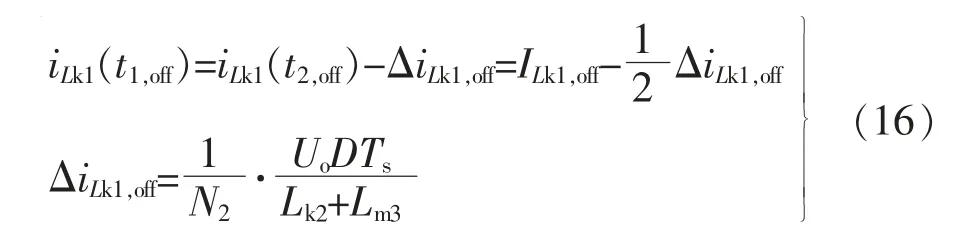
针对励磁电感Lm1， 可知励磁电流iLm1在周期T内的平均值与漏感电流iLk1在Ton阶段内的平均值相等，即

根据输入电流的平均值Iin与ILk1,on，ILk1,off，ID1，off之间的关系，结合式（14）～式（16），得到

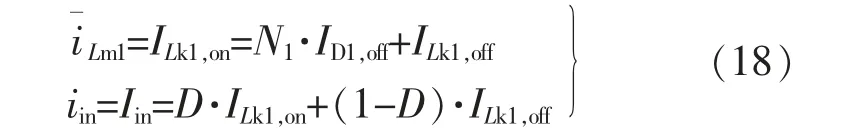
解上式得到

再结合式（1），得到iLk1在Ton内的变化量为

参照式（15）、式（16）、式（19）、式（20），依次可 以 计 算 出ID1，off，ΔiD1ϖoff，ΔiLk1，off，ILk1，on，ILk1，off，ΔiLk1，on的值，并进一步求得iLk1，iD1，iLk2，iD2分别在不同的时 刻t1，on，t1，off，t2，on，t2，off下的值，如表1 所示，指导样机设计及器件选型。

表1 若干变量的表达式Tab.1 Expressions of several variables

5 实验验证

为了验证所提电路工作原理的正确性，根据前节的设计方法， 制作了一台功率为65 W 的实验样机，样机参数如表2 所示。

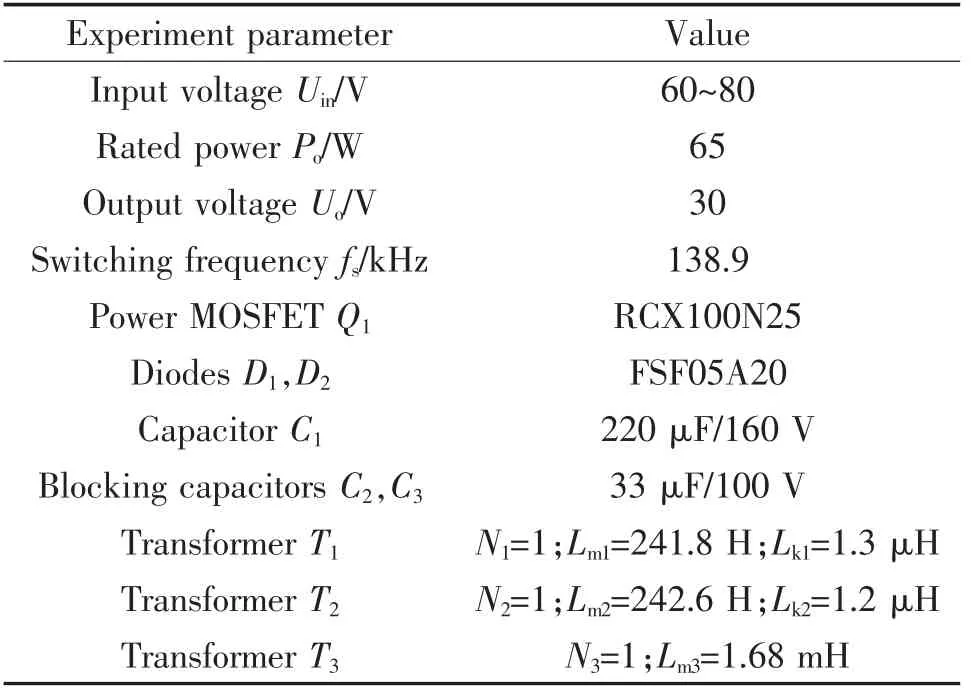
表2 样机参数Tab.2 Parameters of prototype

图6 为所提低输入纹波电流的反激变换器在额定输出状态下，输入电压为70 V 时的稳态工作波形。

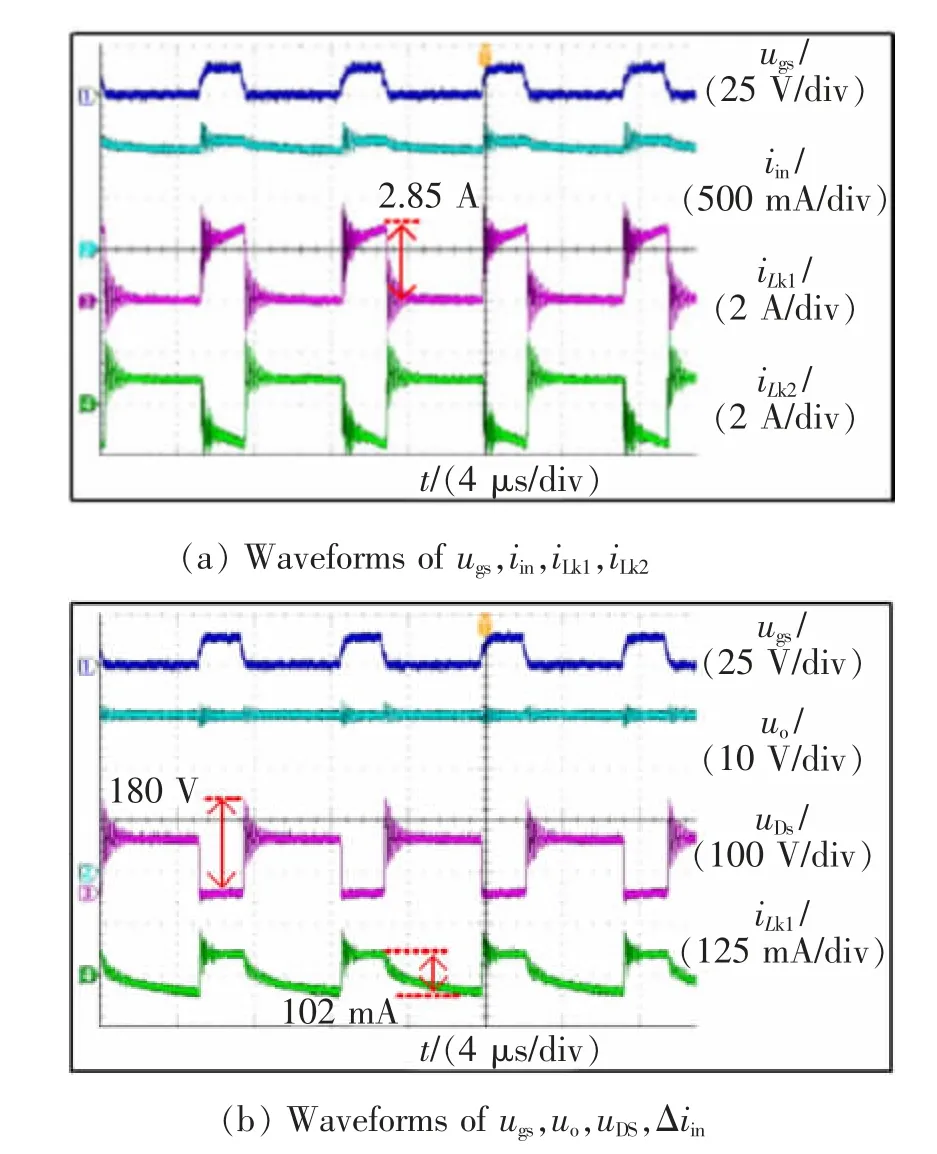
图6 带无源纹波补偿电路的反激变换器的主要工作波形Fig.6 Main working waveforms of flyback converter with passive ripple compensation circuit

此时输入电流iin的平均值约为1.02 A、纹波约为102 mA， 漏感电流iLk1的峰值约为2.85 A，uDS的尖峰约为180 V，符合参数设计。 可以看出，在每个工作状态下，iLk2的斜率与iLk1的斜率几乎互为相反数，说明无源纹波补偿电路产生的漏感电流iLk2对主支路漏感电流iLk1有较好的补偿效果，大大降低了输入侧的干扰。

图7 为在相同条件下，传统反激变换器的稳态工作波形。 分别为开关管Q1的驱动电压ugs、输出电压Uo、Q1的端电压uDs、漏感电流iLk1。 此时漏感电流iLk1的峰值约为3.7 A，uDS的尖峰约为300 V。

图7 传统反激变换器的工作波形Fig.7 Working waveforms of traditional flyback converter

对比图6 与图7， 在传统反激变换器中加入无源纹波补偿电路前后， 输入电流iin由峰值为3.7A的断续纹波电流变为峰值仅102 mA 的近乎直流电流，纹波电流抑制率（γ=1－Δiin′/Δiin）达到了97.2%，这表明无源纹波补偿电路具有极好的纹波抑制效果，验证了理论分析的正确性。 此外，开关管Q1的尖峰由300 V 降至180 V， 表明无源纹波补偿电路的工作特性能够有效抑制开关电压尖峰，减小开关电压应力，减小开关损耗。

图8 为在输入电压70 V、额定输出电压30 V、额定输出功率65 W 的情况下， 加入无源纹波补偿电路前后，输入电流iin的频谱特性对比图，频率为9～30 kHz。 观察可知，加入无源纹波补偿电路后，在整个传导干扰频率范围内，iin的干扰幅值均大幅下降， 其中开关频率fs处的干扰值下降了约30 dB，证明了所提电路对纹波电流抑制的有效性。

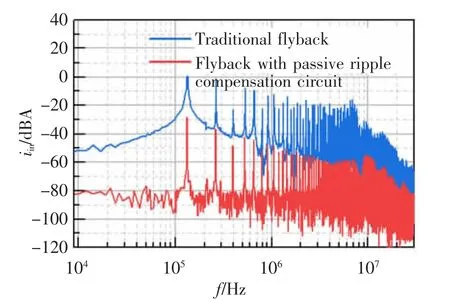
图8 iin 的频谱特性对比图Fig.8 Comparison diagram of spectrum characteristics of iin

图9 为输入电压70 V、输出电压额定情况下，在反激变换器中应用无源纹波补偿电路的前后，系统的效率对比图。 可以看出，加入无源纹波补偿电路后，系统在轻载下（＜27 W）的效率略有降低，但在其它负载范围内的效率大大提高， 满载时的效率由88.4%提升到90.6%，说明无源纹波补偿电路通过抑制开关电压尖峰减小了开关损耗， 提升了整机效率。

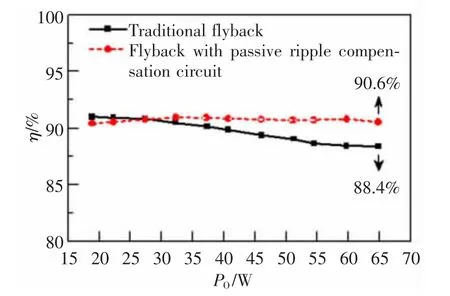
图9 效率对比图Fig.9 Comparison diagram of efficiency

6 结论

以反激变换器为例，针对输入侧固有的断续纹波电流， 提出一种无源纹波补偿电路并进行了研究，得出以下结论。

1）分析了补偿原理，采用时域分析法得到了系统增益和纹波电流抑制条件，给出了变量的计算方法。

2） 实验结果证明不仅纹波电流抑制效果好，而且可以抑制开关管关断电压尖峰，重负载情况下可提高变换器的效率。

3） 其优点为系统稳定、 易于集成和模块化、设计简单、损耗小、与反激变换器的工作互不影响。