K-means 聚类算法研究综述

王 森，刘 琛，邢帅杰

（华东交通大学理学院，江西 南昌 330013）

随着计算机和网络技术的日益成熟， 大数据时代快速发展，每时每刻都在产生大量的数据信息，并且越来越复杂。 而聚类分析是数据挖掘中数据划分和数据分组的重要方法， 一直以来受到众多研究者的关注，在生物学和医学[1-4]、市场营销[5-6]、文本分类[7]、机器学习[8-11]等各个领域得到广泛应用。

聚类算法是一种区别于分类的无监督学习算法，即对无标签的样本点根据数据及数据间的信息关系，对数据对象进行分组。 聚类的最终目的使组内的对象之间相似，不同组中的对象之间有区别[12]。组内的样本点相似性越大，组间相似性越小，则聚类效果越好。 目前广泛研究的聚类算法大致可以分为以下几类：基于层次的聚类，基于密度的聚类，基于原型的聚类，基于划分的聚类。

划分聚类是将数据集划分成不重叠的子簇，使得最终每个数据点恰好位于一个子簇中，而且各个子簇的并恰是整个数据集，经典算法有K-means 算法，AP 算法。 层次聚类是嵌套簇的集族，组织成一棵树。 除去叶节点外，树中每一个结点（簇）都是其子簇的并，树根则是包含所有对象的簇，其中聚类树的构建分为凝聚的层次聚类和分裂的层次聚类，经典算法有AGNES 算法，DIANA 算法。基于密度的聚类则是通过寻找被低密度区域所分离的高密度区域的方法而进行的聚类， 算法有DBSCAN 算法，DPC 算法。

K-means 算法最早是由Mac[13]于1967 年提出，是非常经典的算法，目前仍是非常流行的“十大算法”之一。 该算法由于其原理简单、效率高而被人们广泛使用， 但是聚类结果也易受其他因素的影响，例如K 值的确定，离群点，初始聚类中心的选取，随意选取不同的点作为初始聚类中心将会导致不同的聚类结果，甚至可能陷入局部最优。

首先， 概述K-means 算法的基本思想原理；其次， 分别对关于初始聚类中心的选取、K 值的确定和离群点三方面的改进算法进行基于密度和距离方面的分类总结，分析各个改进算法的优缺点；最后，展望K-means 算法在未来的研究方向和发展趋势。

1 传统K-means 聚类算法

1.1 K-means 算法基本思想

K-means 聚类算法是一种简单的迭代性聚类算法， 是对一个n 维向量的数据点集D={xi|i=1，···，N}进行聚类，其中xi表示第i 个数据点，最终将集合D 划分成k 个类簇。分组的依据主要是“紧密度”或者“相似度”，组内对象越相似、组间差距越大越好[14]。 距离的度量有欧几里得距离、曼哈顿距离和切比雪夫距离， 聚类算法通常用欧氏距离作为相似性度量， 以误差平方和 （sum of squared error, SSE）作为度量聚类质量的目标函数，通过最小化目标函数， 将数据点按照距离聚类中心的远近分成k 个簇。

定义1数据点之间的欧几里得距离

定义2数据点与聚类中心ci间的欧几里得距离公式

式中：ci为第i 个类簇的聚类中心；x 为数据集D 中的数据对象。

定义3误差平方和SSE 计算公式

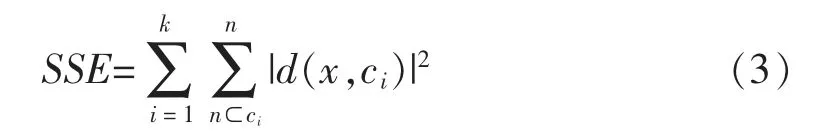
式中：Ci为第i 个类簇；ci为簇Ci的聚类中心；x 为数据集D 中的数据对象；k 为类簇数目。

K-means 聚类算法是一种动态聚类算法，需要进行不断重复迭代。 该算法的基本思想原理是：选择K 个数据作初始聚类中心，其中K 为用户指定的类簇个数。 计算数据点到各个初始聚类中心的距离，将数据点就近分配到各个初始聚类中心所在的集合中形成一个簇。 根据簇中的各个点，更新每个簇的中心。 重复分配和更新的步骤，直到簇不在发生变化，或者目标函数满足条件即可。

2 K-means 算法的改进

2.1 初始聚类中心的选取

K-means 算法中， 初始聚类中心点的选取对聚类结果的影响非常大， 对于不同的初始聚类中心，最终的聚类的结果往往不同，所以K-means 聚类算法的稳定性较差， 并且聚类中心的选择会导致出现聚类结果陷入局部最优的问题。 目前针对初始聚类中心的选择的改进研究主要从密度和距离两个方面入手。

2.1.1 基于密度

目前众多学者提出基于密度的K-means 算法改进方案，主要依据数据集中数据点的密度分布来选取， 避免由于随机选取的初始聚类中心过于密集，导致聚类陷入局部最优的情况。

蔡宇浩等[15]提出了WLV-K-means 算法，通过对局部方差进行加权来优化初始聚类中心。 方差表示了数据的离散程度，方差越小则离散程度越小，密度越大。该算法首先计算样本数据的邻域半径θ和邻域内部的样本数据到样本中心的方差， 以加权的局部方差为新的密度度量。 再对各个样本的加权局部方差进行排序， 将加权局部方差最小即密度最大的数据点作为第一个初始聚类中心。 最后利用改进的最大最小法， 即对加权局部方差作倒数作为密度系数对最大最小值进行加权， 进而找到各个初始聚类中心。WLV-K-means 算法的优点在于引入加权局部方差，提升了计算的准确性，减少了噪声点对聚类效果的影响， 但同时增加了算法时间复杂度和空间复杂度， 针对数据集中样本的数目和分布不同，对应的最优半径调节参数θ也不同，需要多次调节寻找合适的调节参数值。 薛印玺等[16]提出基于样本密度的全局优化K 均值聚类算法KMS-GOSD 算法，该算法通过高斯模型得到迭代初始所有聚类中心的预估计密度， 在更新聚类中心迭代过程中加入偏移操作， 引入衰减因子Ra=（m-1）/m，其中m 为最大的迭代次数，以此逐步降低预估计密度，加速偏移收敛，通过比较实际密度和逐渐减小的预估计密度， 得到密度较高的聚类中心。 KMS-GOSD 算法极大地避免了质心作为聚类中心时陷入局部最优的可能， 降低了算法复杂度， 并且增强了聚类中心点对全局的探索能力，具有较高的准确率和稳定性。

2.1.2 基于距离

目前， 有学者基于欧氏距离提出相异度概念，通过构造相异度矩阵进而判断数据样本点之间的差异，并借此判断数据样本点能否作为初始聚类中心。 孟子健等[17]定义了两个数据点间的第k 个属性的相异度且对数据进行了标准化处理

式中：xik和xjk分别为数据点xi和xj的第k 个属性值；xRk为D 中所有数据点的第k 个属性的所有取值。 并由此给出了两数据点间的相异度公式

式中：N 为数据的维数。

进而构造相异度矩阵

又定义了样本的平均相异度

对于给定的数据点x0，通过计算点x0的相异度参数N（x0，）即以x0为中心，以为半径的区域内点的个数

数据点x0的相异度参数N（x0，r）越大，数据点x0的邻域内的点越多，则x0更有可能为某一簇的初始聚类中心。

计算数据集D 中的每个数据点的相异度参数，并组成一相异度参数集合M，从集合M 中找出最大的参数所对应的数据点作为第一个初始聚类中心，并将该数据点和与该数据点的相异度小于r 的所有数据点从集合M 中删去，重复计算剩下数据点的相异度参数，直到找出K 个初始聚类中心为止。 该算法消除了聚类对初始聚类中心的敏感性，提高了聚类的准确率。 但是该算法的缺点是当最大相异度参数所对应的点不唯一时，不能够合理地选取初始聚类中心。董秋仙等[18]对算法此缺陷进行改进，找出最大的相异度参数值对应的所有样本点xi计算

式中：rij≤，j=1，2，…，p，且构成集合sum，若sum(i)=min sum， 则第i 个样本点即为第一个初始聚类中心。 通过此算法，可在相异度参数最大值不唯一时，找到合适的第一个初始聚类中心，实验表明，此改进算法比原算法具有更高的准确率，同时减少了迭代次数。 廖纪勇等[19]利用欧氏距离定义了数据点间的相异性，均值相异性和总体相异性，构造相异性矩阵，提出了IK-DM 算法。 均值相异性反映了数据点在数据集D 中的分布情况，值越大，则数据点xi的密度越低，与其他点距离越远。 IK-DM 算法通过计算，选取均值相异性最大的点作为第一个初始聚类中心，选择均值相异性第二大的点作为临时第二个初始聚类中心， 通过计算该点与已有初始聚类中心间的相异性，若大于总体相异性，则该点确立为第二个初始聚类中心， 否则找均值相异性次大的点进行判断，依次找出所有的初始聚类中心。 该算法降低了离群点对聚类结果的影响， 有效地选择数据集D 中相异性较大的数据点作为初始聚类中心，避免选择的中心点过于密集，显著提高了算法的稳定性和准确率， 但算法的执行速度较为缓慢，耗时略长。

2.2 K 值的选择

K 值的选取极大地影响了K－means 聚类结果，而聚类算法中K 值的选择往往需要事先指定，且多数是根据历史经验或者多次尝试中得到的。 Rezaee等[20]根据实验证明，最佳K 值位于区间[1，n]中。 为了得到更准确的类簇数目，学界尝试从各个方面对聚类算法进行深入研究，提出了多种改进算法。

2.2.1 基于密度

贾瑞玉等[21]首先通过计算样本密度选出初始聚类中心，在此基础上计算对应不同的K 值时，优化传统聚类有效性指标BWP 为IBWP 指标， 更好地反应了单个数据点的聚类效果，IBWP 指标值越大，聚类效果越好，以此求得最佳聚类数目K。 该算法改进了聚类有效性指标，具有较好的准确性和稳定性，但增加了算法的时间复杂度，运行时间过长。 贾瑞玉等[22]提出CNACS－K－means 算法，该算法重新定义数据点的局部密度， 构造数据集D 的决策图，通过残差分析自动确定类簇数目和初始聚类中心。实验表明，CNACS－K－means 算法在二维和高维数据集上具有较高的准确性，能自动确定聚类类簇数目，该算法的缺点是不同数据集的数据分布会对聚类效果造成一定的影响，对于分布比较稀疏的数据集聚类效果不理想。

2.2.2 基于距离

众多学者基于欧氏距离与误差平方和SSE 来确定聚类数目K，随着K 值增大，则聚类数目越多，类内差距会越来越小且SSE 会逐渐减小。当K 值小于真实聚类数时，随着K 值增大，SSE 下降幅度大，当K 值等于真实聚类数时，再增加K 值，则斜率会迅速增大，随着K 值增大，折线图趋于平缓；因此拐点处对应的K 值多数为最佳K 值。 但是，对于某些数据集来说，“拐点”并不明显，而得到的是一个“拐点区间”， 则无法确定准确K 值， 导致实验出现偏差。 王建仁等[23]改进“手肘法”为ET－SSE 算法，针对“手肘法”中的“肘点”不明确问题进行改进。 改进算法利用指数函数的指数爆炸性质，引入偏执项提高聚类误差较大簇的SSE 的比重，引入权重θ 进行放缩调节使得该算法能更快更准地确定K 值。该算法有效地解决了“肘点不明确”的问题，提高准确率的同时，降低时间复杂度，缺点是权重θ 的调节需要根据实验进行调整， 无法根据最佳权重进行实验。 王子龙等[24]对欧氏距离进行维度加权的改进，并且引入样本点的权重wi和参数τi， 通过改进后的欧氏距离计算样本的密度和权重， 选取密度最大的样本点作为第一个初始中心点， 再利用样本点的权重和参数τi以此得到下一个初始中心点。该算法明显改进了正常数据点与离群数据点到聚类中心的距离， 使得离群数据点到聚类中心之间的距离变大，放大差异，同时，权重的引入避免选取噪声点作为聚类中心，避免聚类陷入局部最优。在中小型数据上，该算法提高了运行速度，减少了算法的迭代次数，但针对大型数据，提高了算法的时间复杂度，耗时较长。

2.3 离群点筛选

聚类过程中，离群点的存在一定程度上影响了初始聚类中心的选取，导致离群点可能成为初始聚类中心，增加了迭代次数，降低了算法效率。 目前对于离群点的研究也成为一个热门方向，众多研究者尝试通过多种方法对数据进行预处理来降低离群点对聚类的影响，以此提升算法效率。

2.3.1 基于密度

唐东凯等[25]提出了OFMMK－means 算法，通过使用LOF 算法——基于密度的离群点检测算法来排除离群点的影响， 再根据最大最小法选取初始聚类中心，进行聚类。 该聚类算法首先对数据集D进行离群点检测， 计算出每个数据点的离群因子值。 数据点的离群因子值分布体现了该点是离群点的概率，值越大，则该点为离群点的概率越大。再根据离群因子值的大小对数据集D 中的数据点进行升序排列，取前αn（0＜α≤1，n=|D|）个数据点作为初始聚类中心的候选集。 最后根据最大最小法[26]在初始聚类中心的候选集上选取距离尽可能远的数据点作为初始聚类中心， 再进行K-means聚类。 OFMMK-means 算法提高了算法的稳定性，具有较高的聚类准确率， 同时， 相较于传统Kmeans 算法，聚类平均迭代次数也较小，但参数α的取值需要依据实验确定，无法得到最佳准确值。杨红等[27]利用LOF 算法进行离群点检测，对数据集进行数据预处理， 得到密集点数据集iris-1 和离群点数据集iris-2， 接着对iris-1 数据集进行K-means 聚类，根据准则函数得到各个簇，其中准则函数作了改进

最后，把离群点数据集中的点根据距离最近原则分配到各个簇中。 该算法主要针对传统准则函数仅仅考虑类内相似性的缺点进行改进，改进准则函数更考虑到类间差异性，放大了聚类效果，进一步优化了聚类结果。 刘凤等[28]利用局部密度离群值检测方法检测并去除数据集D 中离群值，对剩余点进行K-means 聚类，通过DB 指标、Dunn 指标、Sihouette 指标进行有效性评价， 以此评估数据集聚类结果，提高了聚类稳定性。

2.3.2 基于距离

基于距离的离群点检测方法计算简单，可以用于任何可以计算数据点的数据集中，且与数据集的分布无关。 冷泳林等[29]利用基于距离的离群点检测首先随机选一数据点，计算该数据点与其他数据点间的欧氏距离，如果距离大于d 的数据点的比例大于参数p，则认为该点为离群点，依次测验数据集中D 中的数据点，找出所有离群点。 接着，在非离群点中随机选取K 个初始聚类中心， 对非离群点进行K-means 聚类，最后将离群点按照距离最近原则分配到各个簇中。 该算法降低了离群点对与聚类的影响，提高了聚类精度和稳定性，但对于高维数据集来说，聚类效果并不十分明显。 Milos 等[30]研究了基于距离法的高维数据集的离群点检测，发现基于距离的方法可在高维数据中产生更具对比性的异常值分数，通过比较异常值分数进而得到离群点。 此改进算法解决了高维数据集之中基于距离法检测离群点的问题。

3 K-means 改进算法对比分析

表1、 表2 和表3 分别给出选取初始聚类中心的改进算法对比、确定K 值的改进算法对比以及筛选离群点的改进算法对比。

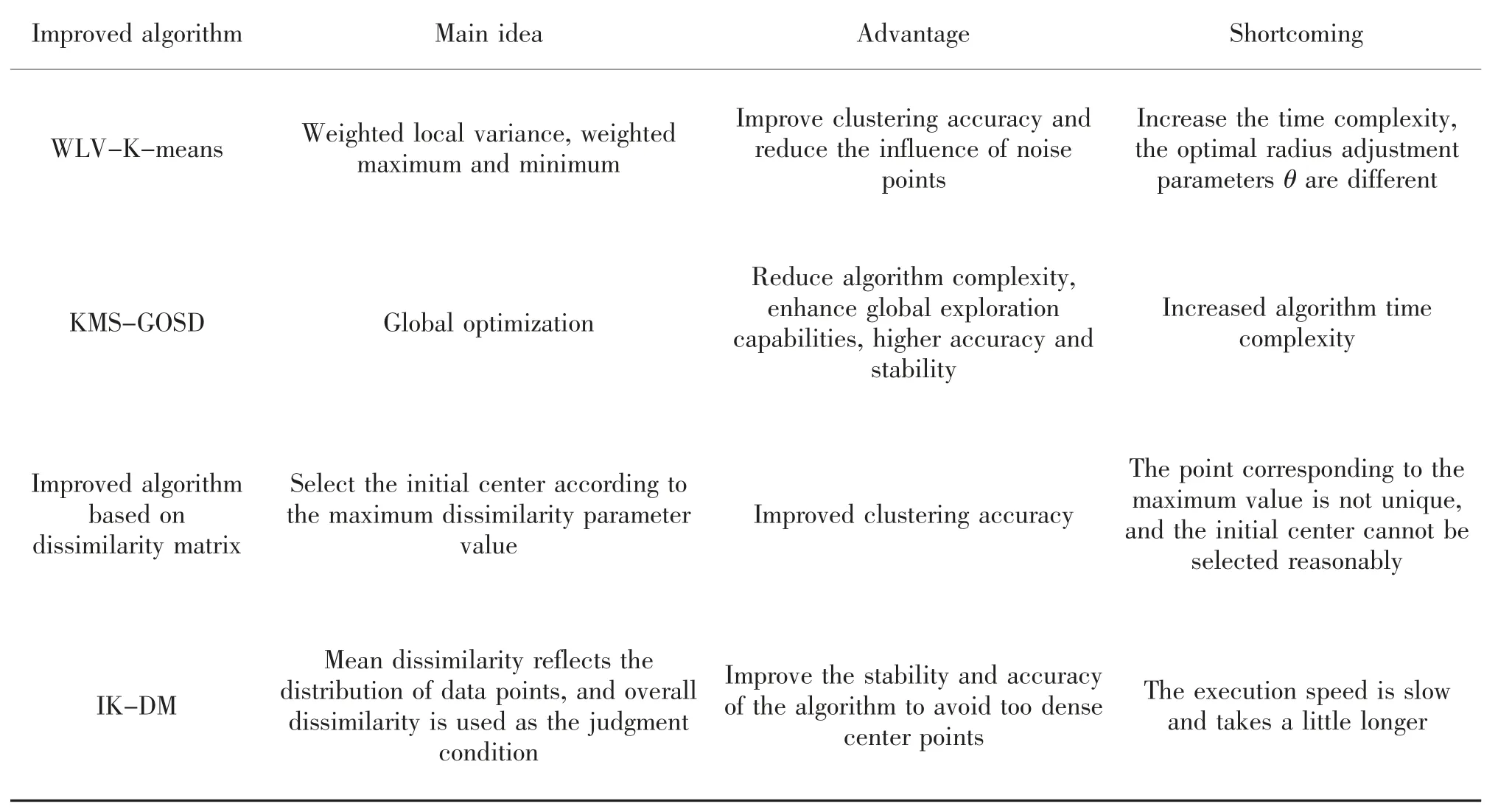
表1 初始聚类中心选取的改进算法对比Tab.1 Comparison of improved algorithms for selecting initial cluster centers

表2 K 值确定的改进算法对比Tab.2 Comparison of improved algorithms for determining K value

表3 筛选离群点的改进算法对比Tab.3 Comparison of improved algorithms for screening outliers

4 结论

K-means 算法是一个极其经典的聚类算法，自提出以来，以其思想简单、聚类速度快、结果良好而得到广泛应用。 但该算法也存在缺陷，本文主要对初始聚类中心的选取、K 值的选择、 离群点的筛选问题进行论述，并且对各个缺陷分别基于密度和距离两个方面进行详细阐述，分析各个改进算法的优缺点。

随着近年来K-means 算法应用领域的逐渐拓宽，学术界对算法进行的改进也逐渐增多，但多数改进算法聚类效果的提高多是以增加时间复杂度作为代价，对于多维数据应用时，算法有效性尚不显著，在后继优化研究中，可以考虑从以下几个方面入手。

1） 在提升聚类效果的同时降低时间复杂度。

2） 考虑提升算法处理高维数据集的能力，随着时代快速发展，各种数据信息繁冗复杂，能够利用K-means 算法快速高效地处理多维数据也是未来重要的研究方向。

3） 目前，越来越多的K-means 改进算法中，多数改进算法会引入参数，但对于参数值的确定需要依据实验经验调试，无法确定准确参数值，这需要进一步研究。