基于自相关分析的交通流预测输入步长研究

王 爽，黄海超，石宝存，陈景雅

（河海大学土木与交通学院，江苏 南京 210024）

随着城市的发展，汽车保有量急剧增加，现有的城市道路交通难以满足日益增长的交通需求，两者之间的供需不平衡导致了交通拥堵、 环境污染、交通事故等一系列问题， 为了解决这些交通问题，智能交通系统（intelligent transportation system，ITS）应运而生[1]。 交通流预测作为ITS 的核心内容，通过计算机技术、大数据挖掘等提前对城市道路交通流及其状态进行预测，从而有助于交通管理者进行车流的合理规划，达到缓解交通拥堵和提高道路通行能力等目的。

目前的交通流时间序列预测模型主要分为基于数理统计的传统预测模型和基于机器学习的预测模型，通过对历史时间序列进行建模以及特征学习，预测未来时刻的交通流量。 自回归积分滑动模型 （autoregressive integrated moving average model,ARIMA）[2]作为典型的基于数理统计的交通流预测模型，在线性数据处理上具有优势，但在大规模非线性的交通数据处理上存在不足。Lu 等[3]将ARIMA模型与LSTM（long short-term memory，LSTM）相结合， 分别利用ARIMA 处理线性数据的优势以及LSTM 处理非线性数据的优势进行交通流预测，验证了该组合模型的多功能性。 随着人工智能和大数据的发展，机器学习模型在处理非线性交通数据上的能力，使其逐渐成为研究者们青睐的交通流预测模型。 机器学习模型中，常用的交通流预测模型有支持向量机（support vector machines，SVM）[4]、随机森林（random forests，RF）[5]、人工神经网络（artificial neural network，ANN）[6]。 SVM 模 型 在1995 年 被Cortes 和Vapnik 首次提出，童林等[7]，闫贺等[8]对SVM 进行改进，提高了短时交通流预测的精度。 针对SVM 求解二次规划问题时训练时间过长等问题，Suyken 等提出了最小二乘支持向量机（least square SVM, LSSVM），有效地减短了运行时长。 谷远利等[9]通过免疫算法优化了LSSVM 的超参数，优化模型训练速度的同时，提高了预测精度。 戴丽珍等[10]通过灰狼算法对LSSVM 的参数进行优化，增强了模型的泛化能力。 Hamner[11]，熊亭等[12]采用了RF进行交通流预测并取得了良好的效果。 LSTM 具有捕捉非线性数据中长期依赖的能力，常被广泛运用在交通流时间序列预测中。 2015 年，Ma 等[13]使用LSTM 对速度进行了预测，并证明了相比较于RNN，SVM，ARIMA 模型，LSTM 在捕捉交通流数据非线性特征以及长时间依赖的优势。

交通流预测的研究主要集中于模型优化，针对输入步长的讨论较少。 林培群等[14]在进行高速公路的行程时间预测时， 选择12 步步长作为不同预测模型的输入，研究预测步长增加后不同模型的预测性能。 王博文等[15]针对LSTM 预测步长增加误差迅速累积的问题对模型进行改进，选取了8 步作为模型输入对未来的1～12 步的时刻进行预测。 Huang等[16]为了验证提出的时间序列分解方法和相应混合预测模型的有效性， 选用12 步作为输入步长进行了多步的交通流预测。 高华睿等[17]在双向长短时记忆网络预测交通流时，采用了滑动窗口模型，以15 步步长作为滑动窗口长度对交通流数据进行重采样， 学习交通流数据随时间变化的趋势变化特征。 金玮[18]利用傅里叶级数提取交通流量的周期性分量特征，分离残差项，选取1、3、6、9、12 作为输入步长分别进行预测， 分析预测结果用来判断模型基于周期性分量的预测效果。 熊亭等[19]将扩散卷积算子应用于GRU（gate recurrent unit）模型进行交通流预测，通过分析1～8 步输入步长对MAPE值的影响， 选择5步输入步长进行特征学习和模型训练。

综上所述，在选择输入步长的方法方面研究较少， 大多直接选择较小的固定步长作为模型的输入， 也有研究通过一些递减的规律来选择输入步长，但这种方法仍依赖于人为的选择。 为了能够自适应地选取输入步长，研究基于交通流时间序列的自相关分析， 将输入步长与本身的数据特征相结合， 采用机器学习模型中常用的LSSVM，RF，LSTM 3 种模型， 探究自相关系数与最佳输入步长之间的关系，最终提出一种基于时间序列分析能够自适应选取最佳输入步长的方法。

1 相关理论

1.1 自相关分析

在时间序列分析中， 自相关函数常用来分析时间序列与其自身k 阶滞后序列之间的相关关系，以此度量历史数据对t 时刻产生的影响。 在交通流数据的自相关分析中， 可以有效地识别时间序列中的周期性特征， 也可以通过相关程度粗略的判断输入数据与预测数据之间的关系[20]。 其中，以k=0，1，2，…，n 表示时间序列的滞后阶数，给定目标预测路段的时间序列{yt}及滞后序列{yt+k},自相关函数定义[21]如下

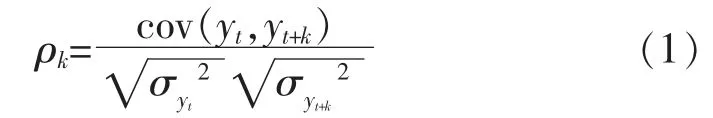
式中：k 为滞后步长；cov（yt，yt+k）为yt与yt+k的协方差；σyt为yt的均方差。

1.2 最小二乘支持向量机

最小二乘支持向量机作为支持向量机的改进模型，不仅可以有效的处理强非线性数据，而且通过简化求解二次规划问题减少了训练时间，极大地增强了LSSVM 的适用性。 与SVM 相同，LSSVM 将交通流数据通过非线性变换映射到高维空间[22-23]

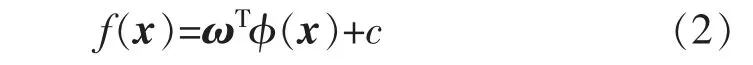
式中：ω 为超平面的权值；c 为常数；φ（·）为空间转换函数。

最小二乘支持向量机的目标函数定义如下

式中：ei为误差；γ 为惩罚因子。

构造拉格朗日函数如下

式中：ai为拉格朗日乘子。 根据KKT 条件可得

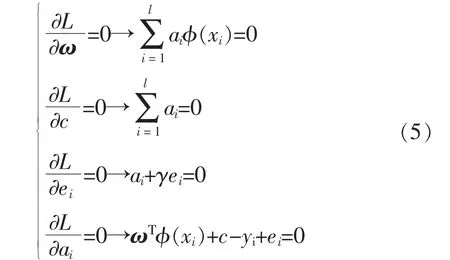
求解式（5），可得LSSVM 数学模型

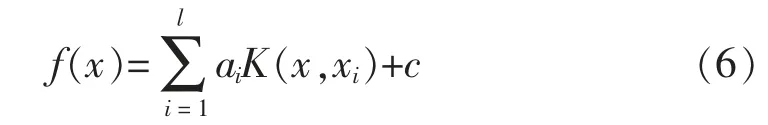
式中：K（·）为模型核函数，通常采用RBF 核函数，即

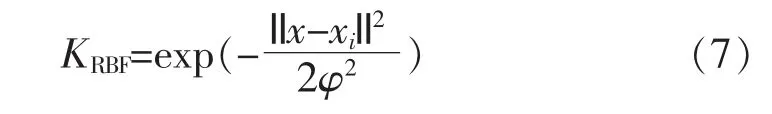
式中：φ 为核函数参数。

1.3 随机森林

随机森林是一种有监督的Bagging（bootstrap aggregating）类集成学习方法，具有强大的数据挖掘和学习能力，在众多领域均有广泛的应用。 在交通流预测研究中， 主要采用随机森林的回归算法，由Bootstrap 法重采样随机形成决策树，大量相互独立的决策树组成森林，将多个决策树预测结果取平均值得到最终的结果，收敛速度快并且具有较高的精确性。 而且随机森林能很好的处理交通流数据中的噪声和异常值，数据随机以及特征随机的特点能够避免训练数据出现过拟合的现象，在大规模的交通流数据中依然可以有效地运行[24]。

1.4 长短记忆神经网络

长短记忆神经网络是一种递归神经网络结构，作为循环神经网络（recurrent neural network，RNN）的一个重要变体[25]，它解决了RNN 中存在的长期依赖和梯度弥散的问题， 通过记忆细胞长时间记忆某个值， 可以更好地捕捉长时间步中时间序列中的规律。典型的LSTM 在RNN 的基础上引入了输入门、遗忘门、输出门来控制信息传递与丢弃。其中，输入门获取输入数据并对其进行更新， 遗忘门给记忆细胞选择权是否维持旧的值，输出门计算并输出结果。

本文将输入时间序列表示为X=[x1，x2，…，xn]，对输入t 时刻数据进行更新

通过更新门和遗忘门对记忆细胞中存储的值进行更新为

输出门输出结果为

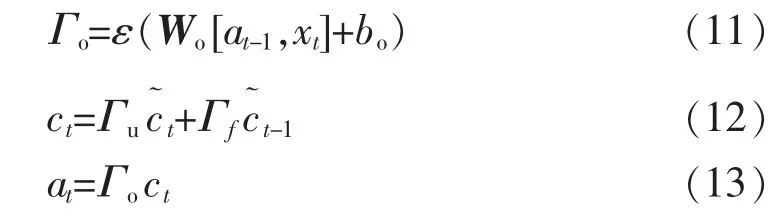
式中：xt为t 时刻的输入； c～t为t 时刻的候选记忆细胞；ct为t 时刻记忆细胞； at-1为t-1 时刻的隐藏状态；Γu，Γf，Γo分别为t 时刻的更新门、遗忘门、输出门的输出；Wc，Wu，Wf，Wo分别为各门的权重参数；bc，bu，bf，bo为偏置参数；tan h，ε 为激活函数。

1.5 交通流预测方法

LSSVM，RF，LSTM 分别作为机器学习模型中二分类、集成学习、神经网络中常用的预测模型，选用这3 种模型研究通过自相关分析选取最佳输入步长的方法。 将车流量时间序列作为预测模型的输入，以不同的输入步长分别进行训练，预测未来15 min 的车流量，取5 次预测误差的均值作为最终的预测结果进行分析。

输入步长的长度以n 来表示，交通流预测的整体流程图如图1 所示。

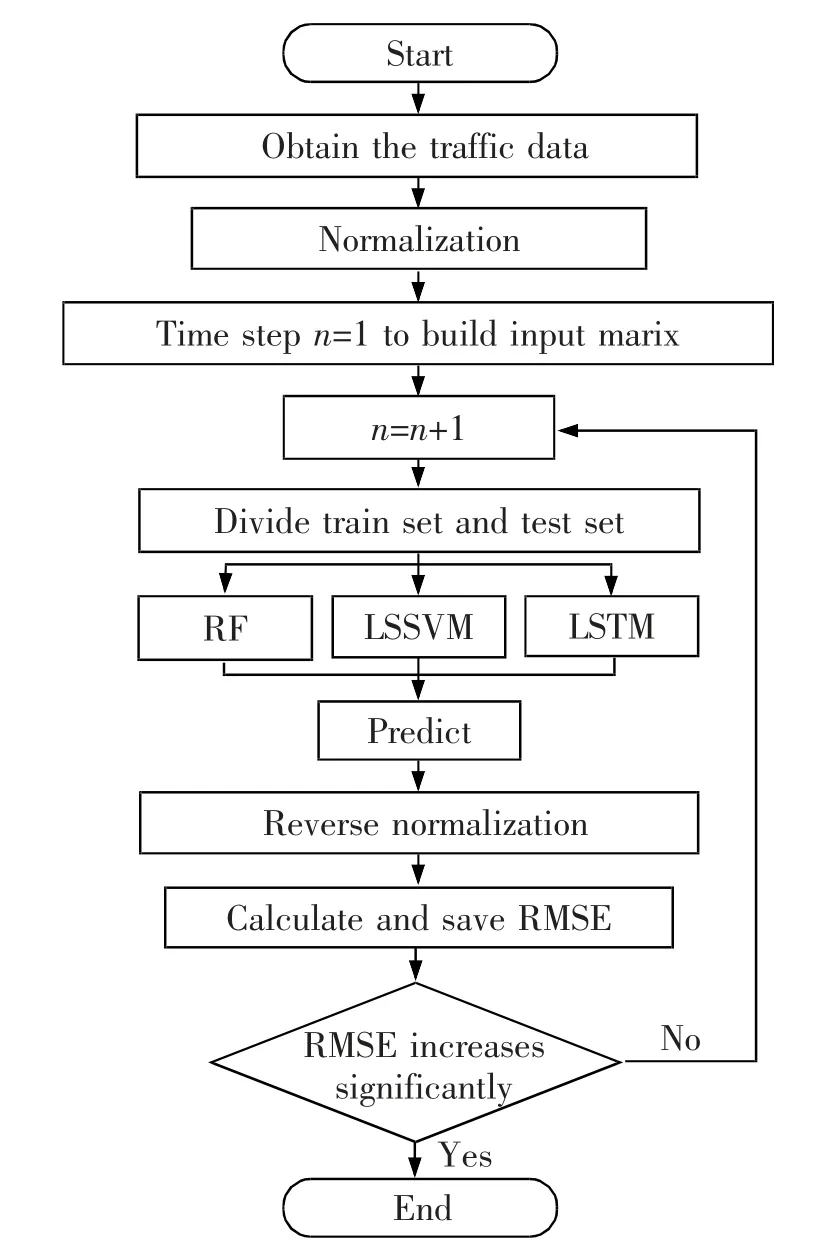
图1 交通流预测流程图Fig.1 Flow chart of traffic flow prediction

2 实例应用

2.1 数据来源及预处理

数据集来源于英国曼彻斯特郡的某个路段的车流量数据， 选取编号为A9094、B26053、B9117、A9116、A9070、A5103 的6 个观测点作为研究对象，为了方便说明，将6 个观测点的编号分别简化为序号1～6。 每个观测点数据集的时间跨度为2020 年1月6 日—2020 年2 月9 日，共35 d，每组数据的采样时间间隔为15 min，样本总量为20 160。

为了能够获得较好的拟合效果，提高模型的收敛速度，本文采用Min-Max 函数对数据进行归一化处理。 按8∶2 的比例划分训练集和测试集， 其中2020 年1 月6 日—2020 年2 月2 日共28 d 作为训练集，2020 年2 月3 日—2020 年2 月9 日共7 d 的数据为测试集。

2.2 模型参数设置及评价指标选取

参数寻优过程保存在网站https://github.com/Team-Cheng/ACF-parameter-optimization-.git 中，寻找各模型的局部最优参数，具体设置如下。 LSSVM模型选用RBF 核函数，模型的性能主要取决于γ 和σ 两个参数， 每个观测点的γ 和σ 分别设置为10、0.1。RF 模型中主要确定最佳叶子数以及树数，在模型训练中每个观测点设置了200 棵决策树，每棵决策树的最佳叶子数为20。 LSTM 模型采用2 层LSTM结构，2 层隐藏层的节点数分别设为32 和16， 添加了Dropout 层来增加模型的泛化能力，设置丢弃概率为0.1。 选用ReLU 作为激活函数， 优化函数选用Adam 优化函数，初始学习率设置为0.005，进行100轮迭代训练，梯度阈值设置为1 以防止梯度爆炸。

采用均方根误差（root mean square error,RMSE）作为指标对预测结果的精确度进行评价，它通过计算预测值和真实值之间的标准差来反映预测结果的准确性，计算式为

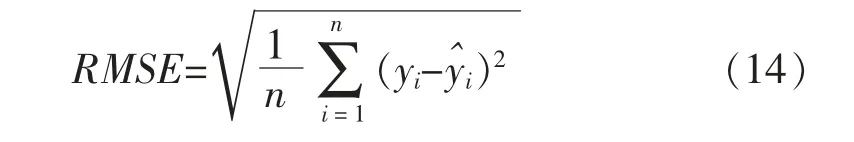
式中：yi为目标预测路段的实际交通流量值；y^i为目标预测路段的预测交通流量值。

2.3 实验结果与分析

首先，确定3 个交通流预测模型输入步长的阈值。 随机选取一个观测点，以输入步长n=1，2，3，…，i 分别进行预测， 观察RMSE 值的趋势变化。 3个模型不同输入步长的RMSE 值如图2 所示。 从对RMSE 进行拟合的曲线图中可以看出， 随着输入步长的增加，LSSVM 模型的预测误差呈现出先减小后逐渐增大的趋势；LSTM 预测结果波动较大，但总体而言，呈逐渐增加的趋势，在48 步之后，有明显增加的趋势； 而RF 模型的RMSE 值随着输入步长的增加呈逐渐降低的趋势。综合LSSVM 以及LSTM 模型的预测结果分析，选择48 步输入步长作为上限。

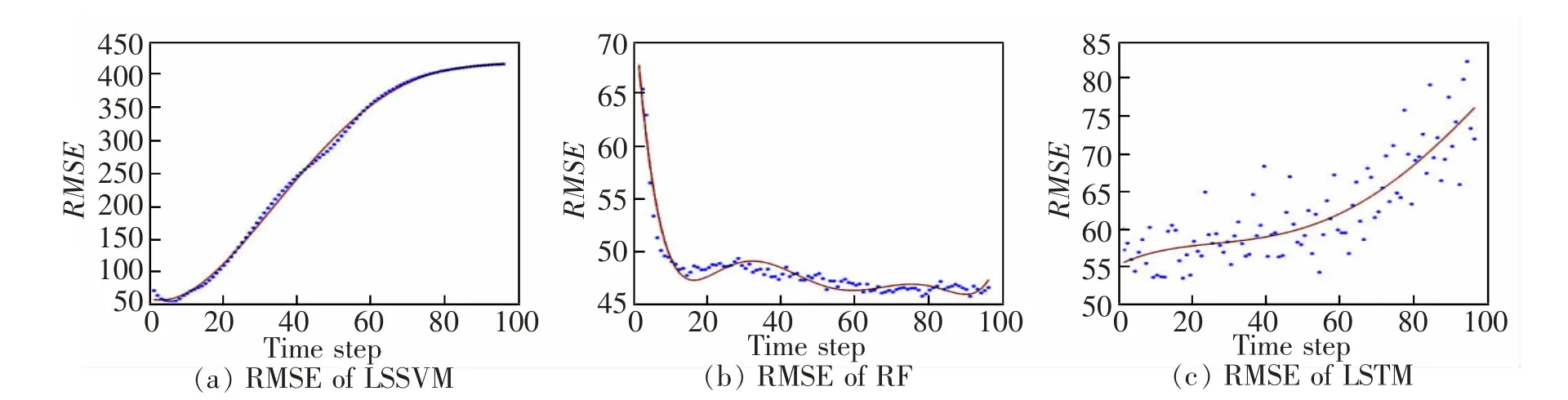
图2 各模型不同输入步长的RMSEFig.2 RMSE of different time step of each model

2.3.1 LSSVM 预测结果

不同输入步长下LSSVM 的预测误差以及自相关系数值如图3 所示。 从对RMSE 进行拟合的曲线图中可以看出， 随着输入步长的增加，LSSVM 的预测误差呈先减小后增大的趋势，当输入步长超过10步后，RMSE 值增加迅速， 输入步长对LSSVM 模型的预测结果影响较大。 结合6 个观测点交通流时间序列的自相关分析，当输入步长的自相关系数值在0.80～0.91 时，LSSVM 会有最小的RMSE 值。

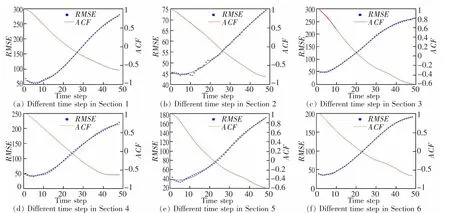
图3 LSSVM 不同输入步长RMSE 及ACFFig.3 RMSE and ACF of different time step of LSSVM

2.3.2 RF 预测结果

不同输入步长下RF 模型的RMSE 值以及自相关系数值如图4 所示。 从对RMSE 进行拟合的曲线图可以看出， 随着输入步长的增加，RF 模型的RMSE 值逐渐减小，有可能存在最小的预测误差，也有可能随着输入步长的增加误差继续减小。 原因可能是RF 模型在训练过程中，输入步长跨度内的交通流数据作为RF 中特征的一部分， 可能受到特征随机性选择或者特征数量对模型预测的影响。 而综合6 个观测点交通流数据的自相关分析， 难以找到相同的规律，通过时间序列的自相关分析寻找预测误差较小的输入步长的方法可能并不适用于RF 模型。

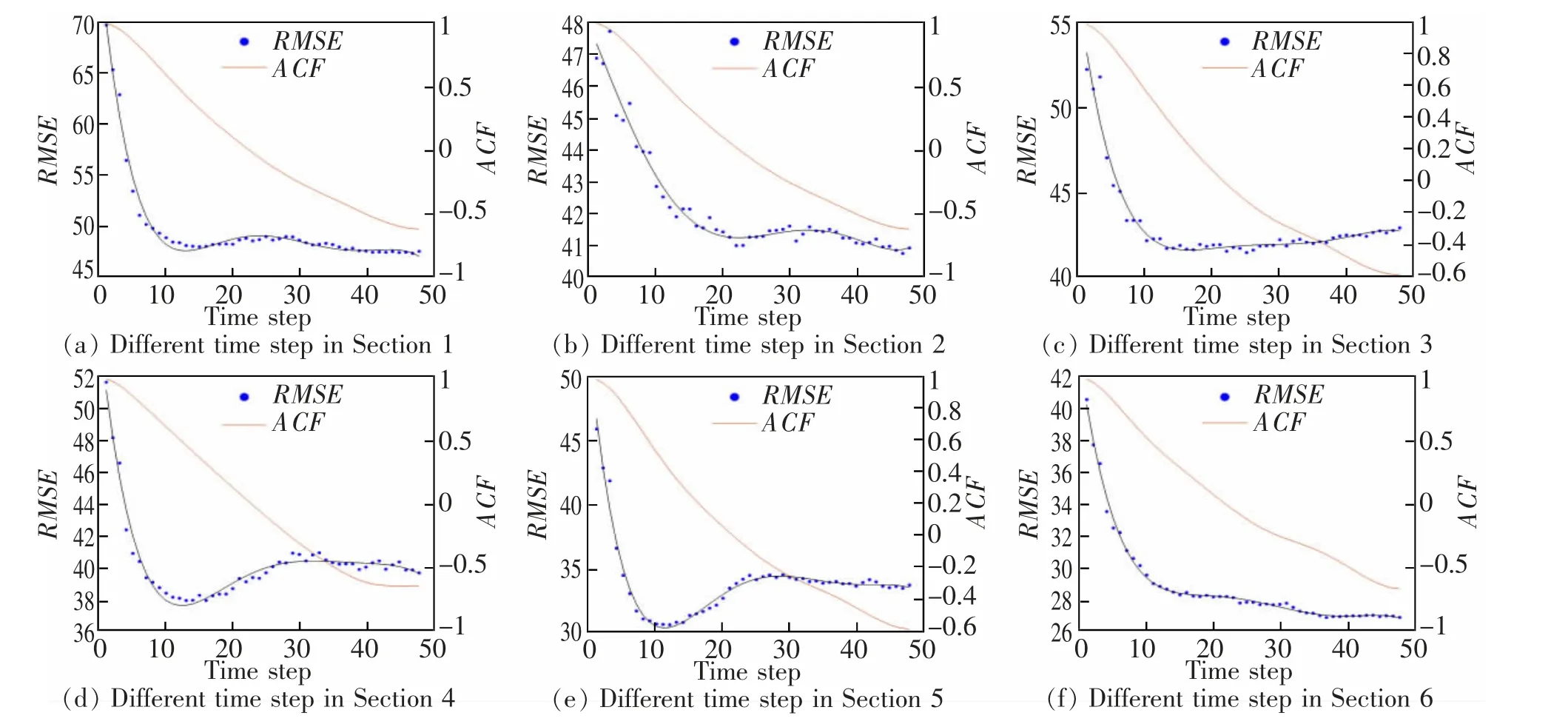
图4 RF 不同输入步长RMSE 及ACFFig.4 RMSE and ACF of different time step of RF

2.3.3 LSTM 预测结果

基于6 个观测点的车流量数据，对各观测点从1 步到48 步的不同输入步长分别进行预测，取5 次RMSE 平均值进行结果分析。LSTM 模型各观测点不同输入步长RMSE 以及相应的自相关系数值如图5所示。 从对RMSE 进行拟合的曲线图可以看出，LSTM模型的预测结果相比较于LSSVM 以及RF 模型，波动程度较大。 但从RMSE 值曲线整体而言，LSTM 预测模型的误差会先呈下降趋势，之后随着步长的增加，RMSE 值呈增加趋势。综合观察6 个观测点达到最小误差的输入步长及相应的自相关系数值，可以发现， 当输入步长的自相关系数在0.47～0.51 之间时，LSTM 可以获得较好的拟合效果和较好的精度。

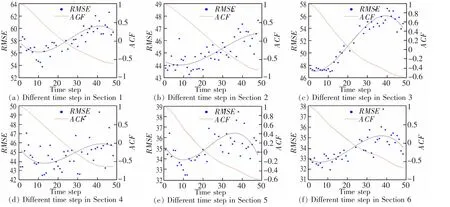
图5 LSTM 不同输入步长RMSE 及ACFFig.5 RMSE and ACF of different time step of LSTM

2.3.4 结果分析

通过对交通流时间序列进行自相关分析，结合3 种模型不同输入步长的预测结果，3 种模型最佳输入步长的自相关系数值如表1 所示。 其中，LSSVM 以及LSTM 最佳输入步长的自相关系数有一定的规律， 通过时间序列的自相关分析，LSSVM可以选取自相关系数在0.80～0.91 的输入步长，LSTM 则可以选取自相关系数在0.47～0.51 的输入步长， 而RF 预测模型中精度较好的输入步长与其相应的自相关系数之间的规律难以找到，数据自相关分析的方法可能并不适用。

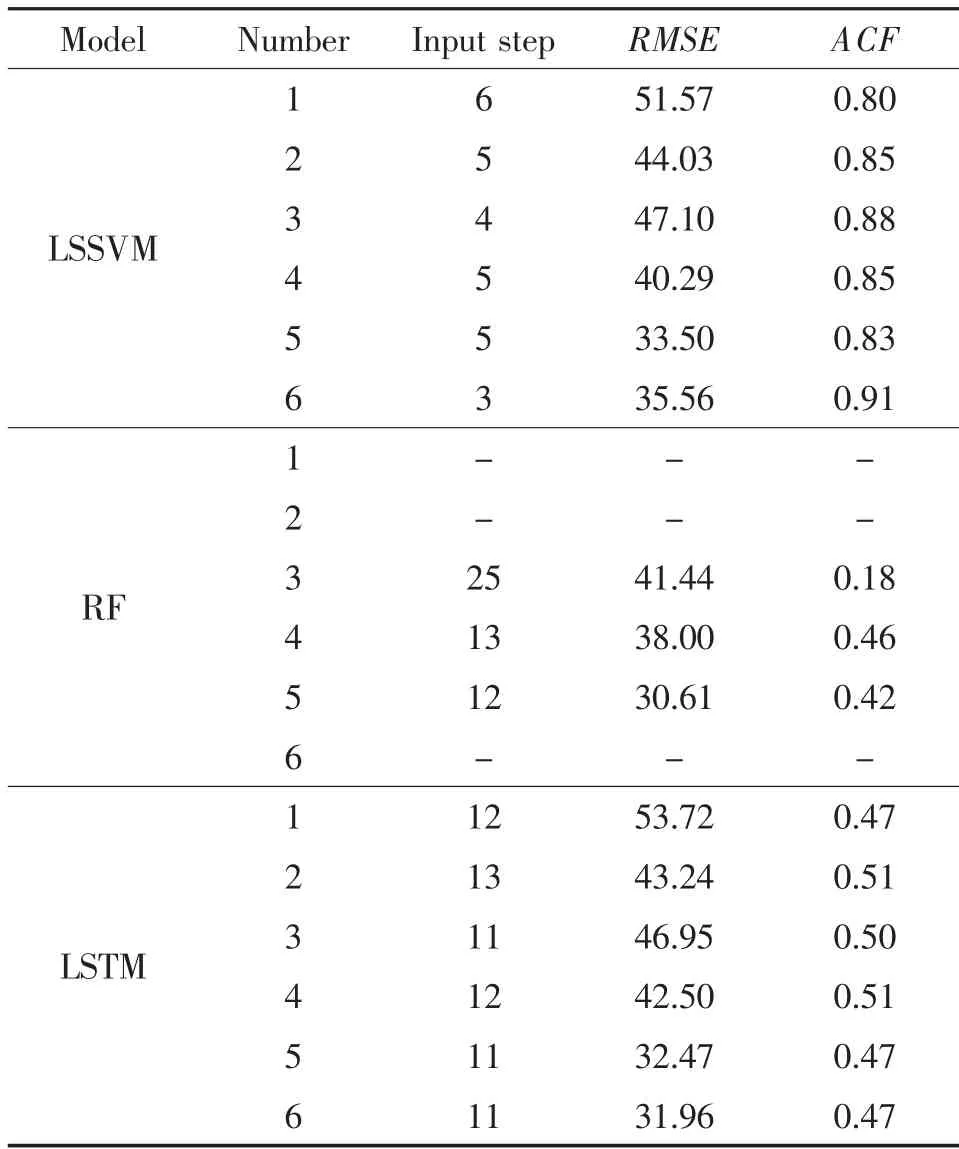
表1 各模型最佳输入步长及自相关系数值Tab.1 Optimal time step and autocorrelation coefficient of each model

3 结论

基于交通流时间序列的自相关分析，选用机器学习中常用的LSSVM、RF、LSTM 模型进行预测，提出一种自适应选取最佳输入步长的方法。

1） 当采用LSSVM 模型时， 建议选用自相关系数值在0.80～0.91 的输入步长，RMSE 值可能有最小值，预测精度较高。

2） 采用LSTM 模型进行交通流预测时，可以选取自相关系数值在0.47～0.51 的输入步长， 预测误差较低。

3） 选用RF 模型进行交通流预测时，预测误差最小的输入步长较大或者自相关程度较低，通过时间序列的自相关分析选择输入步长的方法可能并不适用， 针对RF 模型的最佳输入步长选择方法需要进一步的研究。