基于环境成本的公铁货物运输方式选择研究

叶玉玲，刘 楷，刘佳林

（1. 同济大学交通运输工程学院，上海 201804; 2. 同济大学道路与交通工程教育部重点实验室，上海 201804；3. 上海市铁路智能调度指挥系统工程研究中心，上海 200071；4. 中铁上海设计院集团有限公司，上海 200070；5. 上海市隧道工程轨道交通设计研究院，上海 200235）

“公转铁”实际上是运输结构的调整，最终表现为运输市场上公路与铁路运输方式的货运份额变化。 在运输方式选择行为方面，货主总是选择效用最大的运输方式[1-2]，将运输费用、时间、可靠性、准时性、安全性和便捷性[3-4]作为货物运输方式选择的效用集，并对这些定性属性进行定量化处理[5-6]。 然而这些模型缺乏对路段容量限制、运到时限等约束的考虑，同时在货物单位时间价值的取值上较为随意，与实际情况差距较大。

还有部分学者将不同运输方式组合为综合运输网络进行货流分配，即从整个运输网络的角度，研究在一定供给和需求水平下网络具体弧段的流量，得到交通网络的具体状态[7-8]。 刘杰等[9]以网络运营费用最小化为目标构建多商品网络流模型。Steadieseifi 等[10]和刘星材等[11]则以货流运输费用、扩建和新建费用最小化为目标。 王伟等[12]，杨龙海等[13]综合量化了路径效用值以及货主和承运人运输选择倾向， 构建了适用性更高的货流分配规划模型。 但这些研究对不同品类货运需求特征差异性考虑较少。

交通运输绿色低碳的发展方向使得更多的学者投入到基于环境成本的货流路径选择模型研究中去。 在公铁联运方面，货物运输全程可划分为公路运输、货流转移和铁路运输3 个阶段[14-16]，并将碳排放量转化为相应的碳税成本[17-18]。 Kelle 等[19]则构建了铁路、公路和水路3 种方式并存的多式联运仿真模型，比较考虑环境成本与不考虑环境成本两种情形下运输方式运量的变化。

针对铁路运输而言，部分学者研究了运输参与者在温室气体排放、运输成本和运输时间等方面的利益平衡[20]。然而这些研究仅针对CO2一种气体，并未考虑其他污染气体的环境成本，同时缺少在污染物排放系数和成本因子方面的探讨[21]。

本文从社会总成本的角度出发， 将降低污染气体排放量这一目标转化为降低运输过程中的环境成本， 定量研究环境成本系数不同取值下公铁两网货物运输变化情况， 比较环境成本对运输方式和路径决策带来的变化，对于调整运输结构、控制大气污染、 提升交通运输绿色发展水平具有重要意义。

1 陆路运输环境成本核算

运输环境成本是指运输活动造成环境污染而使环境服务功能质量下降的代价。 运输过程产生的气体污染物主要有SO2、NOx、PM10和CO2，环境成本可以通过各污染物的排放量和污染物成本因子的乘积来测算，计算公式如下

式中：Cp为环境污染成本；R 为能源消耗量；Pi为能源燃烧产生第i 类污染物的排放系数；ci为第i 类污染物成本因子。

1） 能源消耗量。 根据《2019 年中国国家铁路集团有限公司统计公报》和《2019 年交通运输行业发展统计公报》， 铁路单位运输工作量综合能耗3.94吨标准煤/百万换算吨公里，公路专业货运企业消耗1.7 kg/100 t·km 标准煤。

2） 污染物排放系数。污染物排放系数指燃烧单位数量的燃料或其他单位强度的行为过程排放到环境中的某种污染物的数量。 污染物排放量计算按照我国火电行业通用计算标准，即工业锅炉每燃烧1 t 标准煤产生8.5 kg SO2，7.4 kg NOx，1 kg PM10和2 620 kg CO2。

3） 污染物成本因子。污染物成本因子指各种污染物导致的个人健康损害、建筑物损害或农作物减产等环境质量实质性影响的经济价值，衡量的方法可以采用污染当量法进行计算，计算公式如下

式中：Qi为第i 类污染物的排放量；Wi为第i 类污染物的污染当量值；ki为单位污染当量污染物的环境成本。 根据《中华人民共和国环境保护税法》，SO2、NOx和PM10污染当量值和环境成本取值见表1，CO2环境成本为50 元/t。

表1 不同污染物污染当量及环境成本取值Tab.1 Pollution equivalent and environmental cost of different pollutants

2 货物单位时间价值确定

对于货物运输而言，价格和运输时间是货主关心的主要因素，货物运输效益函数构建如下

为了确定货物单位时间价值，可以基于公路和铁路运输方案的费用、 时间消耗以及运量分担率，根据Logit 模型来对参数进行标定，具体公式如下

将式（3）代入式（4），并对等号两边取对数进行变换后有

通过将多组不同OD 货物的公铁运输分担率数据代入式（5），采用多元线性回归即可得到各品类货物θ（u）的取值。

3 货物运输方式选择建模

3.1 问题描述和假设条件

利用图论知识，将陆路运输方式和路径选择组合优化问题抽象为网络G=［V，E，W］，V 为网络中所有节点的集合，V＝｛1，2，3， ……，v｝；E 为网络中所有弧的集合；W 为弧权重集合，即弧段的距离。考虑环境成本的陆路运输方式和路径选择组合优化问题可以描述为：已知公路网和铁路网，将股已知货运量的货流从路网中的起点O 运送到终点D，运输过程中需要途径若干个节点。 已知各种运输方式的单位运输费用、单位时间成本、运输时间、运输能力和污染物排放系数，并已知各种污染物的成本因子。 在满足运输时限、运输能力限制等约束条件的前提下，确定每股货流在起终点间最佳的运输方式以及运输路径决策，使得所有货物的社会总成本之和最小。

假设条件如下：

1） 同一股货流运输过程中不能分割；

2） 任意两节点间公路和铁路的运输速度固定且已知，不考虑突发事件等不确定因素对运输时间的影响；

3）同一品类货物单位时间价值相同；

4）同一股货流只能选择一种运输方式。

3.2 模型建立

将运输费用、 时间成本和环境成本分别记为Z1、Z2和Z3，则其计算公式可以分别表示如下

式中：Fm为第m 股货流的货运量，m∈N，N 为所有货流的集合，N=｛1，2，3，…，n｝；为第m 股货流采用k 运输方式的单位运输成本，k∈A，A 为所有运输方式的集合，A=｛1，2｝ 分别为公路运输、 铁路运输；为节点i 和节点j 之间采用k 运输方式的运输距离，i，j∈V；vk为k 运输方式的平均运输速度；为k 运输方式s 污染物排放系数，s∈B，B 为所有污染物的集合，B=｛1，2，3，4｝ 分别为SO2、NOx、PM10和CO2；cs为s 污染物成本因子；为决策变量，=1为第m 股货流在节点i 和节点j 之间采用k 运输方式，否则=0。

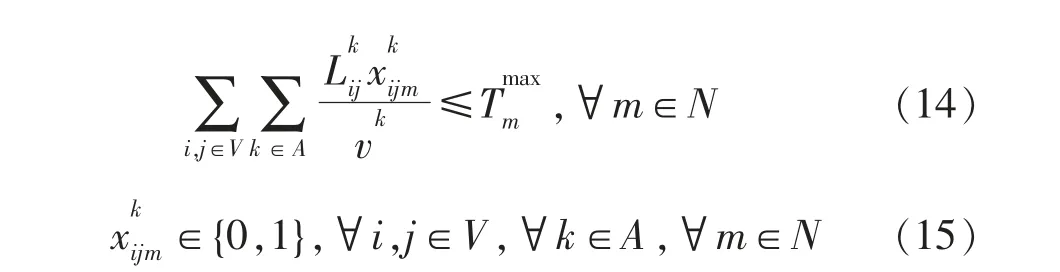
为了考虑环境成本对货流运输方式选择的影响，即比较环境成本系数不同取值下公铁两网货流量的变化情况， 将目标函数表示为min Z=Z1+Z2+αZ3， 可以通过调整环境成本系数α 的值改变环境成本的大小，α=0 即表示不考虑环境成本对货流分配的影响，α=1 即按照当前实际环境保护税征收标准下考虑环境成本对货流分配的影响。 模型的约束条件具体如下式（9）和式（10）表示对于任意站点，每股货流最多只能经过一次；式（11）表示对于某一股货流，运输过程中不发生中转；式（12）表示对于某一股货流，其运输路径的任意两个相邻节点之间最多只能采用一种运输方式；式（13）表示任意两个相邻节点之间某一种运输方式所承载的运量不大于其运能限制， 其中表示节点i 和节点j 之间采用k运输方式的运输能力限制；式（14）表示每股货流运输时间不得超过其最大容许运到时间， 其中表示第m 股货流的运到时限；式（15）为决策变量约束。

4 算例分析

4.1 算例描述

以山东省实际公路网和铁路网布局数据为原型，选取公路网中的高速公路和铁路网中的普速铁路，分别构建陆路运输系统中公路网和铁路网结构图，如图1 和图2 所示。 图中弧两侧数字表示两点间距离。

图1 实例路网中的公路网结构图（单位：km）Fig.1 Highway network structure diagram in the case（Unit：km）

图2 实例路网中的铁路网结构图（单位：km）Fig.2 Railway network structure diagram in the case（Unit：km）

所选案例共分为224 支货流，总运量145.6492 万t，货物品类分为6 类，每支货流均有其最大容许运到时间。 公路和铁路整车运输的单位成本计算公式如式（16）所示。 其中，公路和铁路不同运价号货物的c1、c2取值见表2。

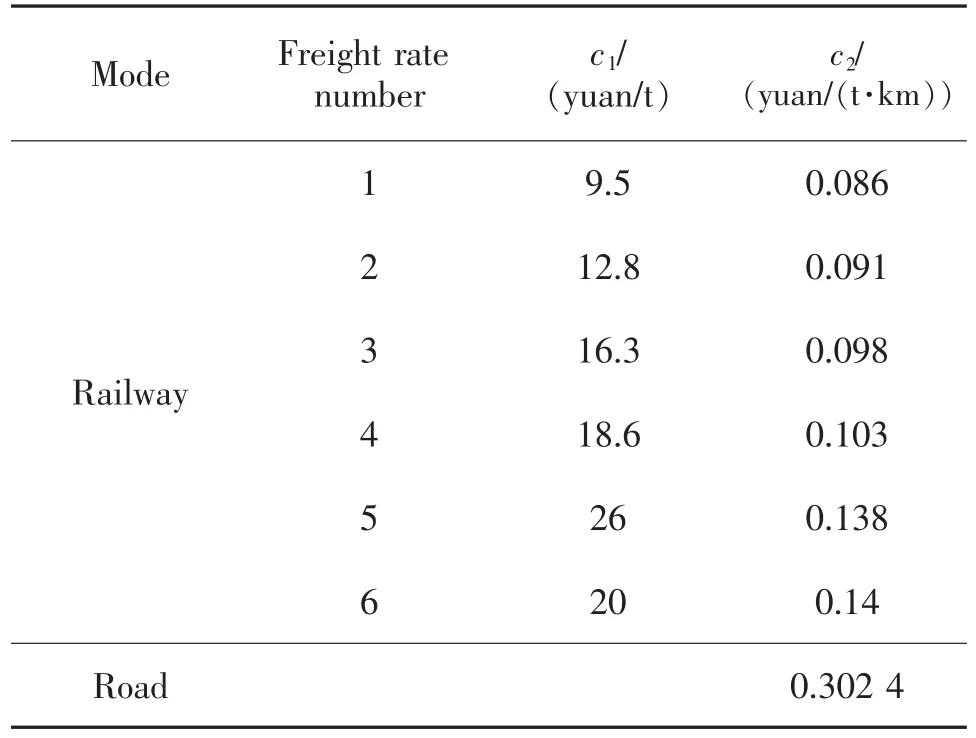
表2 公路和铁路单位成本系数取值Tab.2 Unit cost coefficient of highway and railway

公路运输速度取70 km/h， 铁路运输速度取33 km/h。 根据济南局管内非平行运行图货车使用能力近似得到铁路网各区段运输能力，由于所分析的货物品类仅为大宗货物，对该能力做相应扣除；根据高速公路通行能力近似得到公路网的运输能力，同样也对该能力做相应扣除。

4.2 实例求解及结果分析

利用遗传算法进行求解， 相关参数取值如下：种群大小为300，最大交叉概率为0.8，最小交叉概率为0.5， 最大变异概率为0.05， 最小变异概率为0.005，最大迭代次数设为3 000。

将不考虑环境成本的货流运输方式选择模型记为模型1，此时α=0，其目标函数为min Z=Z1+Z2。将考虑环境成本的货流运输方式选择模型记为模型2，此时α=1，其目标函数为min Z=Z1+Z2＋Z3。

1） 公铁货运情况对比分析。 通过对模型1 和模型2 得到的公路网和铁路网货运结果分析可知，公路网货运比重显著高于铁路网， 其原因主要在于本文选用实例数据中较大比例的货物是相邻城市间短途货运需求，对于运输时间要求较高，而公路运输速度较快，公路运输货运周转量远高于铁路。 模型1 和模型2 得到的公路网与铁路网具体货运情况见表3。

表3 货物运输方式选择情况Tab.3 Selection of cargo transportation mode

从表3 可以看出，在考虑环境成本后，铁路承担的货流数量、 货物运量及周转量均有一定程度的增加，其中公路货运周转量下降3.24%，铁路货运周转量上升36.31%，对运输结构起到一定的调整作用。

在公路货运比重显著高于铁路比重的背景下，当前环境成本占社会总成本比重较低，导致其对公转铁运输方式转移的影响有限。 为了比较环境成本变化对于货流运输方式选择的影响，调整环境成本系数的取值， 提高环境成本在社会总成本的比重，从而得到公路与铁路货运周转量随环境成本系数变化的情况（图3）。

图3 公路与铁路货运周转量变化情况Fig.3 Changes in road and railway freight turnover

根据图3 中曲线变化趋势可知，随着环境成本系数的增加，公路货运周转量不断下降，而铁路货运周转量则呈现增长趋势，公路运输相对于铁路运输竞争力开始减弱。 这主要归功于铁路运输较公路运输在污染气体排放方面的优势。

模型1 与模型2 分品类的224 支货流运输方式选择情况见表4。 计算结果显示，模型2 与模型1相比，1、2、4、6 号品类部分货流由公路转移至铁路，运价率最低的1、2 号品类货流转移效果更为显著。由于路段容量限制等原因，3、5 号品类部分货流由铁路转移至公路，以保证总成本的最低。 可以看出，在公路货物运价率相同的情况下，铁路运价率越低的货物，其公转铁转移效果越显著。

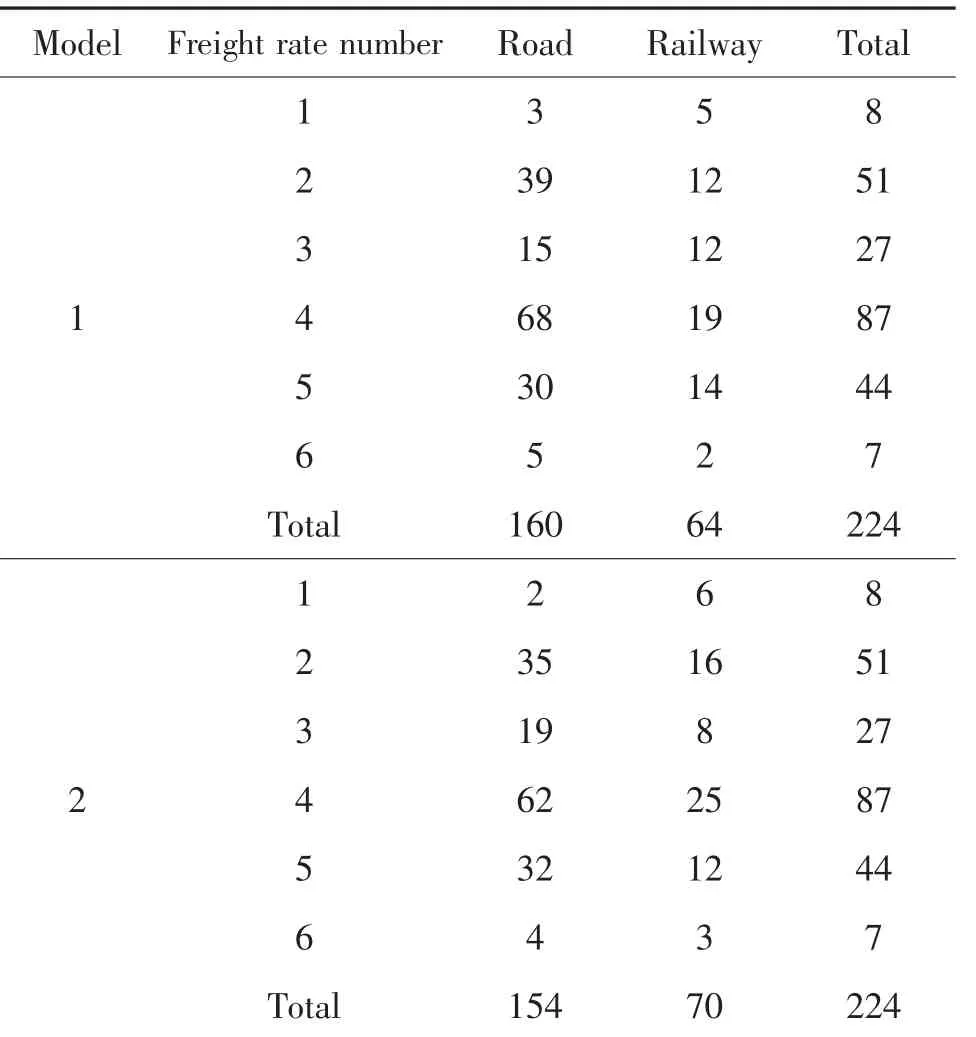
表4 分品类货流运输方式选择情况Tab.4 Mode selection of freight flow by rate number

2） 成本对比分析。虽然与模型1 最优解的目标函数值相比， 模型2 最优解的目标函数值增加了0.46%，但这只是目标函数值的对比，无法反映实际社会总成本的变化。 将模型1 中各类污染气体折合为相应的环境成本，并纳入总成本中，具体各类成本情况见表5。

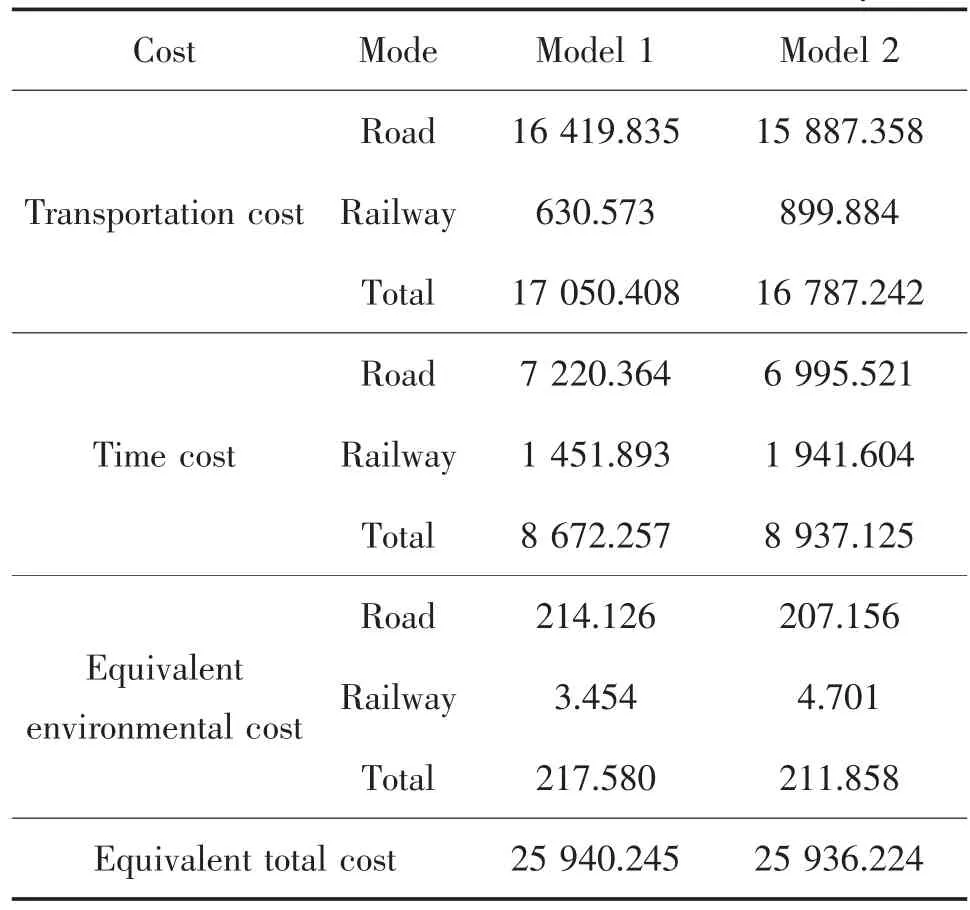
表5 模型1 与模型2 各类成本比较Tab.5 Costs comparison between Model 1 and Model 2×104 yuan

经统计分析，与模型1 相比，模型2 运输成本减少1.54%，时间成本上升3.05%，折合环境成本降低2.63%，最终导致折合总成本有一定程度的降低，从模型1 的25 940.245 万元降低为25 936.224 万元，降幅为0.016%。 即考虑环境成本能够降低社会总成本。 但由于环境成本在社会总成本中占比较低，所以对运输结构调整影响较低。

3） 污染物排放对比分析。模型1 与模型2 各污染气体排放情况见表6。

表6 模型1 与模型2 污染气体排放情况Tab.6 Pollutant gas emission of Model 1 and Model 2

计算结果显示，模型2 与模型1 相比，SO2，NOx，PM10和CO2排放量分别降低2.615%、2.614%、2.623%和2.615%，即考虑环境成本的货流运输方式选择具有一定的减排效果。 由于环境成本在社会总成本中占比较低，污染气体减排效果较微弱。

表7 为不同环境成本系数取值下各类污染气体的排放量对比，随着环境成本系数α 的提高，货主所需支付的环境费用不断增加，货流转移量逐渐加大，各类污染物排放量逐渐降低，产生一定减排效果。

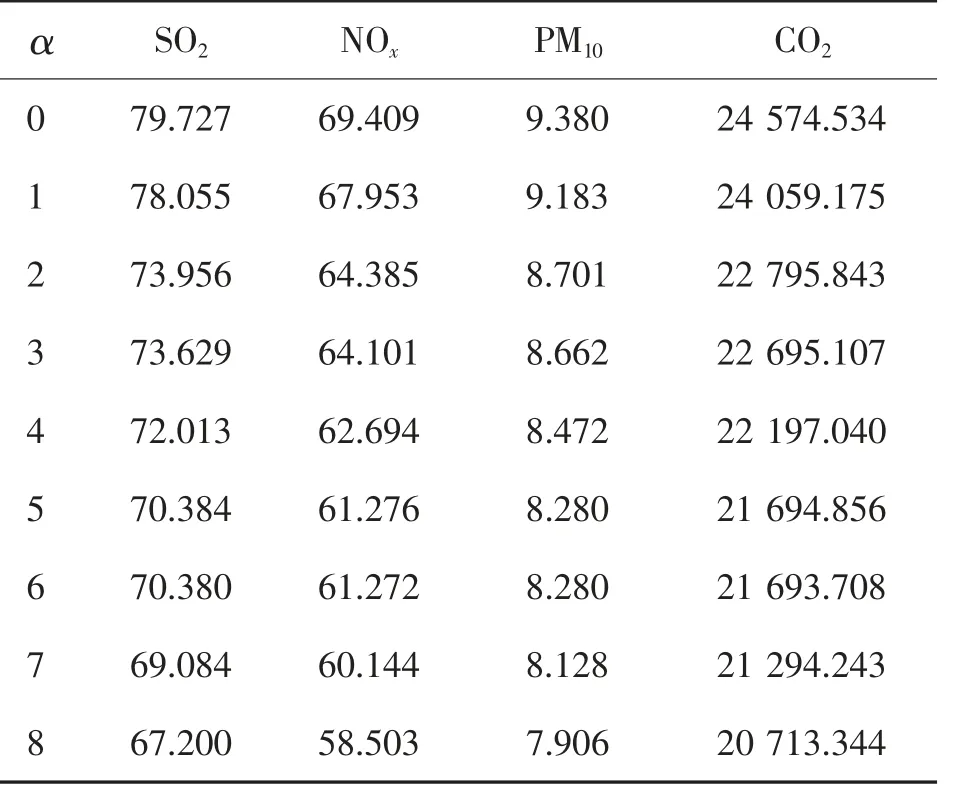
表7 不同环境成本系数污染气体排放情况Tab.7 Emission of pollutant gases with different environmental cost coefficients t

5 结论

1） 本文从社会总成本的角度出发，将降低污染物和温室气体排放量这一目标转化为降低运输过程中的环境成本，并据此对运输方式和路径选择组合优化模型的目标函数进行调整，运用运输方式和路径选择组合优化模型对这一转移量和影响进行了量化研究。 最后以山东地区公路网和铁路网货运数据为原型，研究不同环境成本参数取值下的陆路运输方式和路径选择决策， 将理论应用到实际，验证了优化模型的合理性与求解算法的可行性。

2） 通过对比可以发现，鉴于铁路运输在运输成本及环境成本方面的优势，随着环境成本系数的增加，部分货物会从公路转移至铁路运输，降低了整个运输系统的运输成本，各污染物的排放量都有一定程度的降低。 同时较低的环境成本费用也导致了货流转移效果较为微弱。

3） 未来，文中货主运输方式选择模型将在考虑运输费用、运输时间和环境影响因素外，进一步考虑运输安全、 便捷性和货物自身价值等其他因素，同时基于货主个体的异质性开展不同影响因素对货主方式选择的敏感性分析，深入探讨多式联运体系下各类货物运输方式的市场占有率。