基于联合特征参数的卫星单-混信号调制识别研究

杨洪娟 时统志 李 博* 赵 楠 王 钢

①(哈尔滨工业大学(威海)信息科学与工程学院 威海 264209)

②(大连理工大学电子信息与电气工程学部 大连 116024)

③(哈尔滨工业大学电子与信息工程学院 哈尔滨 150001)

1 引言

调制识别技术自电子侦察成为现代化战争中军事对抗的重要手段便引起了学者广泛而深入地研究。当关键情报信息被捕获后，作为非协作通信的第三方，调制类型的识别在一定程度上就决定了后续信号处理的信息质量[1,2]。因此，正确识别信号常用调制方式具有重要的应用价值。1998年，成对载波多址(Paired Carrier Multiple Access, PCMA)被首次提出[3]。在PCMA系统中，通信双方在同一频带上发送两路数字调制类型相同的上行信号，经卫星混合转发后，协作双方接收到相同的PCMA信号，从而节约了系统带宽，增强了信号的抗干扰截获能力和系统吞吐量[4]。

目前，单载波信号调制识别算法已经比较成熟，但基于PCMA的信号前端处理-调制识别却鲜有人研究。文献[5]提出了一种基于最大似然准则和高阶累积量的PCMA信号调制识别算法，充分考虑了混合信号的频偏影响，识别率良好但识别类型较少，局限性强。文献[6]在原有累积量的基础上引入信号瞬时特征统计量完成了对卫星单-混信号的调制识别，算法的运算时间得到了降低，但对个别信号识别处理的参数选取不当，识别率不佳。文献[7]在文献[5]的基础之上优化了特征参数并结合4次方谱线对混叠信号进行调制识别，拓宽了算法的应用范围，提高了识别率但选取参数仍然较多，识别要求很高。此外，近年来将深度学习模型引入调制识别的研究也逐步开展，相关模型有：卷积神经网络(Convolutional Neural Network, CNN)[8]、循环神经网络(Recurrent Neural Network, RNN)[9]以及一些混合模型[10]，整体算法的识别性能有所提高，但所需数据量及计算复杂度都相对较高。

针对目前识别算法存在的不足，本文利用高阶累积量和星座图聚类特性设计了一套简单可行的PCMA调制识别算法，单载波调制类型主要包括二进制相移键控(Binary Phase Shift Keying,BPSK)、正交相移键控(Quadrature Phase Shift Keying, QPSK)、8移相键控(8 Phase Shift Keying, 8PSK)、16正交幅度调制(16 Quadrature Amplitude Modulation, 16QAM)、64正交幅度调制(64 Quadrature Amplitude Modulation,64QAM)，PCMA信号由单载波调制混合而来。具体而言，通过构造4 个联合特征参数可以对{BPSK、BPSK混、QPSK、QPSK混、8PSK、8 P S K 混、1 6 Q A M、1 6 Q A M 混、6 4 Q A M、64QAM混}共10种调制信号进行较为准确地识别，仿真实验结果表明，调制方式为多进制相移键控(Multiple Phase Shift Keying, MPSK)、多进制正交幅度调制(Multiple Quadrature Amplitude Modulation, MQAM)的卫星单混信号在正常通信所需的信噪比(Signal-to-Noise Ratio, SNR)下能够维持高识别率。

2 信号模型

根据发射功率的不同，PCMA系统可分为对称模式(P1=P2)和非对称模式(P1̸=P2)[11]。通常PCMA系统工作在对称模式下，每一个通信终端发送一个功率相同的上行信号，经卫星中继进行混叠后转发给各个地面基站。其传输机制如图1所示。

在不考虑特殊信道的情况下，通信终端及侦听方接收的信号复基带一般模型为

3 特征参数选取

3.1 高阶累积量

高阶累积量具有表征含噪基带信号的星座点分布、抑制高阶高斯噪声的特性，因此被广泛应用于调制识别领域[12]。由于PCMA混合信号的高阶累积量与单载波信号相比有明显的差异，所以选取累积量作为识别的特征之一。

对于具有0均值的复平稳随机过程{X(t)}，其P阶混合矩为

其中，E表示数学期望，X*(t)为X(t)的共轭函数。

随机信号的高阶累积量与混合矩之间存在如式(6)的关系

对于特征参数F1,F2,F3，选取实验数据长度为5000个符号，信噪比SNR范围为[–5, 20]，对每一个信噪比进行1500次蒙特卡洛实验。特征参数F1对各参数的分离效果如图2所示。在图2(a)中，信噪比变化对高阶累积量的影响很小，各个参数的6阶累积量相对稳定并且相对差异较大，为了突出图2(a)中下半部分差异及确定划分阈值，特将其放大，如图2(b)所示。由于MQAM(混)高阶累积量比较接近，这里划为一类。分类阈值的选择方案是各调制方式理论推导值的算数平均值，综合图2可以准确地区分BPSK, {QPSK, 8PSK、BPSK混}、{16QAM, 64QAM}、{QPSK混、8PSK混}、{16QAM混、64QAM混}，其阈值分别为20, 6, 3, 1.5。

图3给出了特征参数F2对BPSK混与{QPSK,8PSK}两类信号的分离效果曲线图，从图3中可以看出，在较低信噪比下F2也能保持良好的分离性，通过F2可以非常容易区分两类调制方式。图4给出了特征参数F3对剩余调制类型的识别分离特性，特征参数F3可以将F1,F2识别过后未分离的{QPSK,8PSK}、{QPSK混、8PSK混}逐一识别，各分类阈值为2, 2, 1。

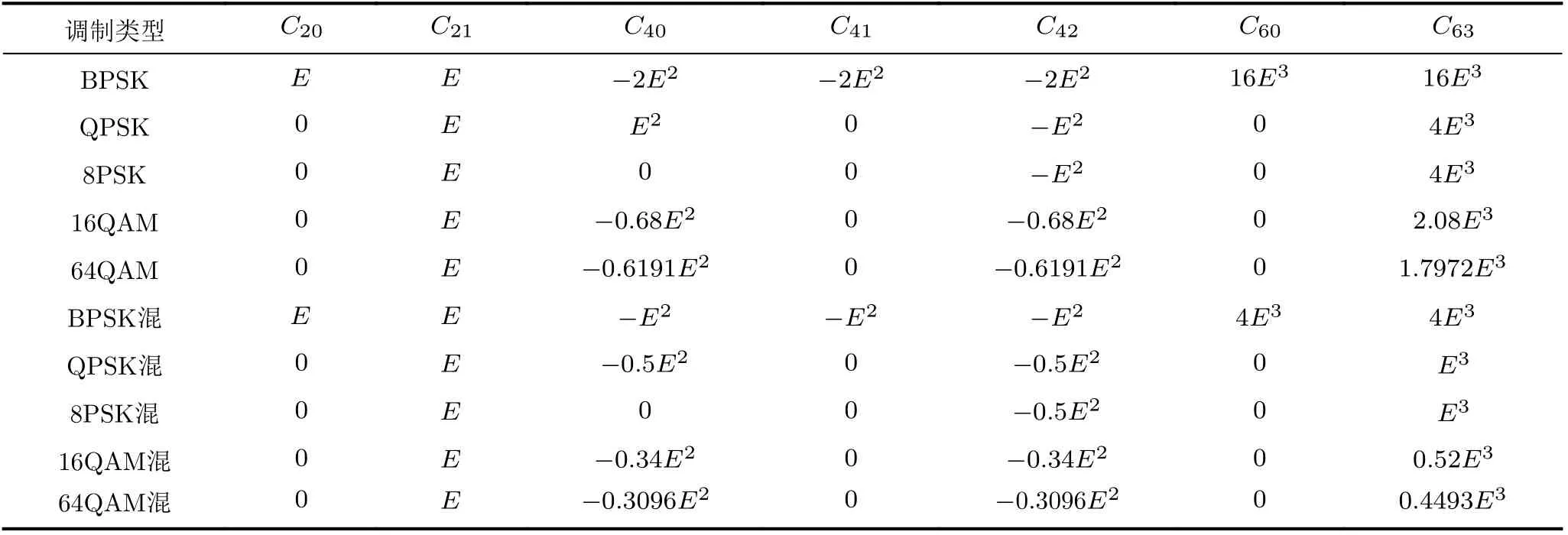
表1 单-混信号高阶累积量理论值

3.2 星座图聚类特性

对于MQAM调制信号，其星座图特性反映了信号的矢量端点的空间分布状态信息，图5、图6分别给出了方形16QAM(单-混)、64QAM(单-混)信号在理想状态下的星座图，由图可知，MQAM不同调制阶数之间的星座图差异明显，其中信号端点个数和端点间的距离等差异完全可以用于调制分类，需要特别注意的是，当随机数据量变化时，星座图会呈现簇状聚集。因此，MQAM信号进行聚类分析以及联合距离函数进行多参数判决对调制识别具有重要价值。

3.2.1 减法聚类算法

3.2.2 参数联合的聚类算法

根据理论计算可以得到标准R参数的值，对于方形MQAM单混信号，标准半径rmax,rmin以及Rs如表3所示。

表3 MQAM信号的rmax, rmin, Rs理论值

信号的数据长度决定了聚类算法的识别效果，为有效利用原有数据量，本文根据星座图的对称性，将星座图中的坐标点投影到原点所在的横坐标轴上，将星座图聚类分析转变成投影点聚类算法。以16QAM为例，投影后的示意图如图7所示，假设原有每时隙数据点为160，则投影后每处聚点数据量为160/4=40，为原有聚点160/16=10的4倍之多，随着MQAM调制阶数增大，数据量扩大成正比关系。同时考虑到投影带来的距离半径的变化，因最小半径和最大半径成比例变化，标准半径Rs未发生改变。综上，MQAM(混)信号的各理论值调整总结如表4所示。

表4 MQAM信号的rmin, Rs, Ns 理论值

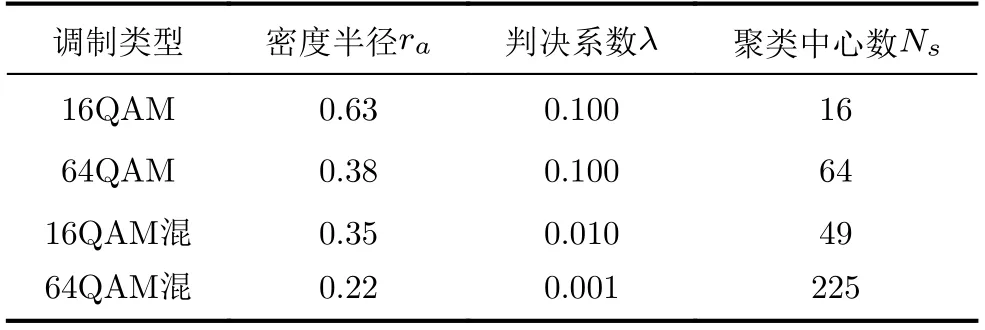
表2 MQAM单混调制信号聚类中心及相关系数

4 识别流程

使用随机产生的调制信号作为信号源，对接收到的信号进行必要的预处理，主要包括载波同步、相位同步、定时同步、信号过采样、下变频等。根据所设计的特征参数通过仿真来确定合适的分类阈值。具体分类实现步骤如下所示：

(1) 选取F1=2|C63|作为分类特征，用于区分BPSK,{QPSK, 8PSK、BPSK混}、{16QAM,64QAM}、{QPSK混、8PSK混}、{16QAM混、64QAM混}，选定阈值为20, 6, 3, 1.5；

(2) 选取F2=|C60|作为分类特征，用于区分{QPSK, 8PSK}和BPSK混，选定阈值为2；

(3) 选取F3=4|C40|作为分类特征，用于区分QPSK与8PSK、QPSK混与8PSK混，选定阈值为2,1；

(4) 选取改进的减法聚类星座图作为分类特征，用于区分16QAM与64QAM，16QAM混与64QAM混，判断依据为星座图阶数N以及与标准R 参数的联合评估函数E。对于{1 6 Q A M,64QAM}，当N ＜6且E1＞0.8时为16QAM；当N ＞6且E2＞0.8时为64QAM；对于{16QAM混、64QAM混}，当N ＜11且E3＞0.8时为16QAM混；当N ＞11且E4＞0.8时为64QAM混；

根据选取的分类特征和判定的阈值条件，构造的分类决策树如图8所示。

5 仿真实验及分析

根据由决策树建立的识别流程进行统一的仿真验证，设定信号源调制类型为{BPSK、BPSK混、QPSK、QPSK混、8PSK、8PSK混、16QAM、16QAM混、64QAM、64QAM混}。信源随机生成0,1序列，不同调制方式采用不同的串并变换，随机序列符号长度为5000，信源编码为格雷码，码长100。随机信号调制载波频率f1=f2=10 MHz，采样频率fs=60 MHz，过采样倍数为10，符号速率fb=2.5 Mbit/s。信道传输噪声为高斯白噪声，PCMA信号混合幅度比为1∶1，分量信号的归一化频偏Δf1=Δf2=1×10-4，相位偏移θ1=θ2=2π×10-4。

针对不同类型信号，信噪比取值范围[–5, 20]，步长1 dB。在每个SNR处进行1500次蒙特卡洛仿真实验。对得到的结果取平均值，不同调制方式的单混信号识别率随信噪比变化如图9所示。从图9可以看出，采用高阶累积量对卫星单-混信号的调制识别成功率在2 dB之后就达到95%以上，充分体现了其有效性。

为了验证改进的减法聚类算法对于MQAM单-混信号的识别效果，表5显示了本算法在相同初始条件下对PCMA等信号识别率的仿真结果。从表格的识别情况可以明显看出，采用改进的星座图聚类算法对MQAM调制的单-混信号在15 dB处识别率均达到95%以上。

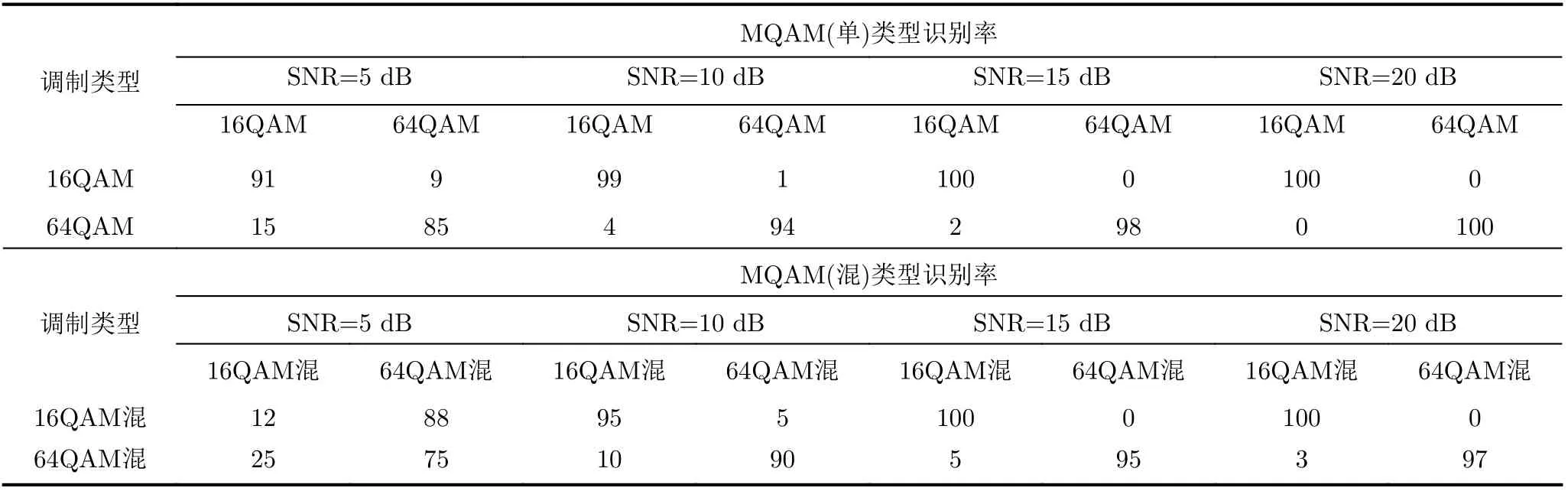
表5 星座图聚类算法下的MQAM信号识别率(%)

一般情况下，数据序列长度越长，信号调制方式的识别效果越好。我们在原有基础上限定信号信噪比为20 dB，针对不同调制信号仿真获取正确判定信号所需的最少数据序列长度，最少序列长度的判定标准是1000次实验中至少有950次可以正确识别信号类型。实验结果如图10所示。

图11给出了本文算法与已知算法的性能比较，相较于文献[14]所提出的星座图特征聚类(Clustering of Constellation Signature, CCS)算法，本文算法在低信噪比下与其识别率相当，但随着SNR的增加，本文算法普遍优于CCS算法；文献[15]提出的遗传编程-K最近邻(Genetic Programming-K Nearest Neighbor, GP-KNN)算法鲁棒性相对较好，低信噪比下的识别性能优于GP-KNN算法，但高SNR处识别效率远低于本文算法。此外，高阶累积量和聚类特性的结合也拓宽了两种不同信号的调制类型，提供了调制识别的新的实现方法。

6 结束语

本文利用高阶累积量和星座图聚类特性来识别卫星通信中单载波和PCMA信号的调制类型，将MPSK, MQAM类调制信号的4,6阶累积量和改进的星座图减法聚类结合成统一的识别算法。在未知通信双方内容的情况下，本算法为实现对单-混盲信号的调制识别提供一种实现方法，并在此基础上提升了识别效果，降低了复杂度，具有一定的应用价值。但是在本文中，只考虑了高斯信道中的分离效果性能，其他信道对系统的影响还有待继续研究。