基于密度泛函理论的团簇NiCo2S4异构化反应研究

曾鑫渔，方志刚，毛智龙，王 倩，朱依文，郑新喜

（辽宁科技大学 化学工程学院，辽宁 鞍山 114051）

化石燃料逐渐消耗导致环境污染问题日益严重，寻找高效、清洁和可持续能源以及开发新型能源存储设备来满足人类的日常需求成为当下的研究热点[1]。根据目前已有研究成果可知，氢气为具有高能量密度的无污染能源，是新能源的主要研究对象。获取高纯度氢最有效的方法之一是电催化析氢（HER）[2]，而该方法可以通过采用过渡金属催化剂来提高电解水效率，从而达到产生足量氢气的目的。超级电容器（SC）是新能源存储设备的主要研究对象，其具有高功率密度、长循环寿命和优异安全性等特性，可分为电双层电容器（EDLC）和赝电容器（FS）两类，前者在电极/电解质界面上分离电荷，后者依赖于在电极表面附近发生的法拉第氧化还原反应来进行电荷存储[3]。

设计FS机制的微结构以加快电荷转移速率和富集电活性位点，成为实现高功率和高能量密度的SC最可行的方案，该设计关键在于提高所使用的以过渡金属化合物材料为主组成的电极材料活性。因此，无论是HER的高效电催化剂，还是SC的先进电极材料都迫切需要开发出一种具有优质结构和电化学活性的材料[4]。二元过渡金属氧化物表现出丰富的氧化还原反应，可在多种组分间产生协同效应而备受关注，然而这些材料通常具有低电导率和比容量[5]，限制了其的进一步应用。因此具有相同优点且同时兼备高导电性和高功率密度的二元过渡金属硫化物进入科研人员的视线，成为极具潜力的催化剂和电极材料。其中Ni-Co-S体系因其具有比单金属硫化物更丰富的氧化还原反应和更优异的电化学活性而受到了广泛的关注[6]，如NiCo2S4

[7]。然而NiCo2S4自身的电化学性能还不能满足作为催化剂或电极材料所需[8]，许多科研工作者尝试去通过改变NiCo2S4结构来促进其催化或电化学性能，如HUI等[9]采用环氧树脂填充、炭化和水热生长NiCo2S4纳米棒的方法，制备出具有更优异电化学储能性能的电极材料；WANG等[10]将镍钴配位聚合物作为前驱体金属模板经过硫化、碳覆和烧结等步骤得到长循环、高稳定性的NiCo2S4杂化材料。

在已有文献中，对于Ni-Co-S体系的研究大多是以实验设计为主，缺乏基础理论上的研究，而理论可以为实际实验提供方向或避免不必要的失误，且材料的结构稳定是其发挥出优异性能的基础。因此本文将由拓扑学原理[11]构建团簇模型后，基于密度泛函理论[12-13]和过渡态理论对非晶态合金NiCo2S4的异构化反应进行分析，了解各构型间的相互转化关系，从而判断其局域结构稳定性，借此筛选出最稳定的优化构型，为进行相关实验的科研人员提供结构参考和理论支撑。

1 模型与计算方法

利用拓扑学原理，改变原子的位置并结合基本几何结构排列组合，设计了近50种团簇NiCo2S4的初始构型。B3LYP杂化泛函能够较为准确预测体系平衡结构、能量和频率等性质，尤其在过渡金属的优化计算占有优势，而且其用时较少，是目前运用最为广泛的泛函之一。Lanl2dz赝势基组是使用较为普遍的有效核势基组之一，常应用于包含过渡金属体系的计算。因此采用密度泛函理论中的B3LYP杂化和Lanl2dz赝势基组对初始构型进行结构优化和频率等参数运算，对Co、Ni和S原子使用ECP加double zeta优化[14]，并在S原子上添加极化函数ξS,d= 0.55[15]。化学动力学的主要理论基础为过渡态理论，因此对反应过渡态（TS）使用二次收敛自洽场（SCF）近似法得到其总能量。

过渡态理论是以量子力学对反应过程中的能量变化的研究为依据，研究其中出现的较高活化络合物即过渡态的理论。QST2方法是常用的寻找过渡态的方法之一[16]，在计算过程中假设反应路径在势能面上是一条二次曲线，再以路径上的能量最大点作为过渡态。因此通过QST2方法和过渡态理论相结合对优化构型进行二次优化运算，排除没有虚频数及优化结果能量低于反应物或生成物的过渡态[17]。优化收敛条件均为最大作用力＜ 0.00045，均方根作用力＜ 0.0003，最大位移＜ 0.0018，均方根位移＜ 0.0012。所有计算均在计算机HP Z440中采用Gaussian 09软件完成，以此确定团簇NiCo2S4异构化反应过程中过渡态的空间结构。

2 结果与讨论

2.1 团簇NiCo2S4的优化构型及过渡态构型结构

团簇NiCo2S4的7种优化构型中，单重态有2种，三重态有3种，如图1所示。另外异构化反应中的过渡态构型有3种，如图2所示。以能量最低的构型 1(3)为参考零点（设其能量值为 0.000 kJ/mol），其中图1编号右上角括号内数字表示重态，编号后括号内的数字表示相对能量；图2中白键表示反应前后没有基本变化的键，绿键表示即将生成的键，虚键表示即将断开的键。5种优化构型的空间结构分别为五棱双锥型（1(3)、3(3)和 1(1)），单帽四棱双锥型（2(3)、2(1)）。

图1 团簇NiCo2S4优化构型Fig.1 Optimized configurations of cluster NiCo2S4

从图2可以看出，反应3(3)→2(3)成键5根（Ni1—S4、Co6—Co7、Co6—S2、Co7—S2 和Co7—S4），断键 3根（Ni1—Co7、Ni—S3 和Co7—S3）；反应1(1)→ 1(3)成键两根（Co2—S5 和Co3—S4），断键 1 根（Co2—Co3），反应 2(1)→ 1(1)成键 1 根（S4—S5），断键7根（Ni1—Co2、Ni—S5、Co2—S4、Co2—S5、Co2—S6、Co3—S6 和Co2—S7）。

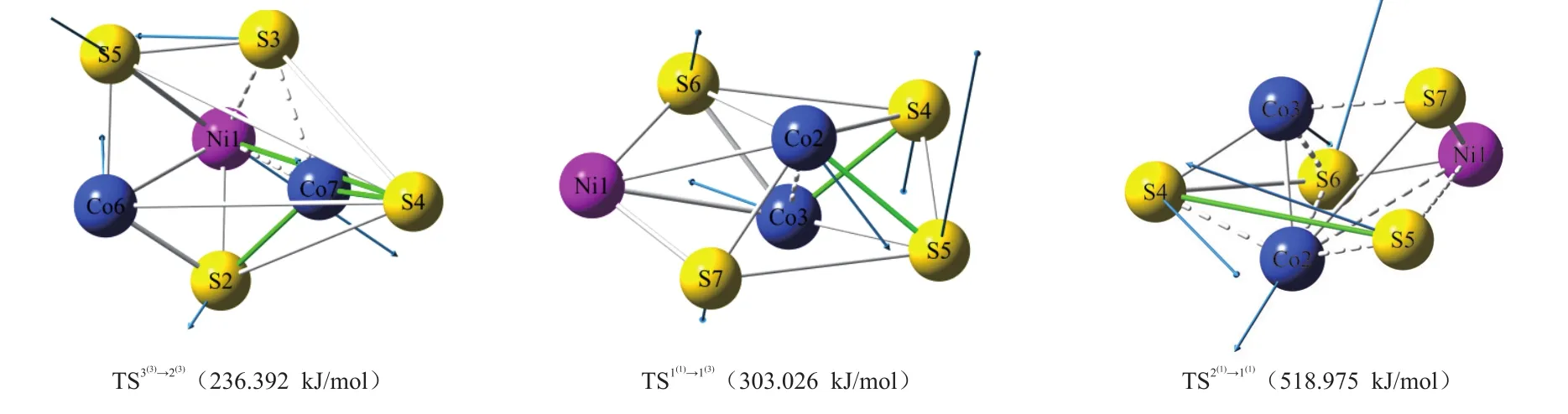
图2 团簇NiCo2S4过渡态构型Fig.2 Transition state configurations of cluster NiCo2S4

2.2 团簇NiCo2S4异构化反应的热力学研究

2.2.1 团簇NiCo2S4的优化构型热力学参数

团簇NiCo2S4异构化反应的本质是从相对不稳定的构型转化为相对稳定的构型，因此各优化构型的热力学性能决定了反应发生的可能性。假设团簇NiCo2S4的生成路线为Ni + 2Co + 4S → NiCo2S4，热力学参数的变化量计算公式如式(1)～式(3)所示。

式中，X代表热力学参数U、H、G和S；U为热力学能，kJ/mol；H为焓，kJ/mol；p为压力，kPa ；V为体积，m3；T为温度，K；G为吉布斯自由能，kJ/mol；S为熵，J/(K·mol)。

式(1)中括号内的计算如式(4) 所示。

式中，C为常数。

团簇NiCo2S4热力学参数变化量的变化趋势与其优化构型的对应初始值保持一致，故在后续分析中直接用X代表各项热力学参数数据，分析X变化趋势。将各优化构型的初始热力学参数如表1所示。从表1中可以看出，团簇NiCo2S4各优化构型的U、H和G变化趋势一致，从1(3)到2(1)，U、H和G均逐渐减小，说明随着生成团簇NiCo2S4时放出的热量逐渐减少，构型稳定性逐渐减弱，生成团簇的难度逐渐升高。

可推导出团簇生成反应的吉布斯自由能变与各优化构型的热力学参数之间的关系，如式(5)和式(6)所示。

结合表1 数据可计算出H-U= 2.478 kJ/mol（除构型 2(3)为 2.481 kJ/mol），说明ΔpV基本为常数，即在反应过程中团簇NiCo2S4的体积与压强之积基本不发生变化，表明在定温、定压条件下，ΔG由构型的U和S共同决定。由U和S数据可知，二者在不同重态间发生了较大变化，而在不同结构间的变化不太明显，说明构型自旋多重度是引起ΔG发生变化的主要因素之一。

表1 团簇NiCo2S4优化构型的U、H、G和STable 1 U, H, G and S of optimized configurations of cluster NiCo2S4

2.2.2 团簇NiCo2S4异构化反应限度和方向

由范特霍夫方程（Van，t Hoff equation）可得反应平衡常数K定义式如式(7)所示。

式中，R为摩尔气体常数，8.314 J/(mol·K)。

团簇异构化反应各项热力学参数如表2所示。在定温、定压条件下，吉布斯函数可作为判断反应是否自发的依据，ΔG＞ 0表明化学反应正反应自发；ΔG＜ 0 表示逆反应自发；ΔG= 0 表明产物与反应物处于平衡状态。由表2可知，ΔrGm均＞ 0，表明3个异构化反应均可正向自发进行。当K＞ 1时，反应正向进行限度大于逆向，且K越大反应进行越彻底，一般认为K＞ 105表明正反应较为完全。表2中K值大小排序为 1(1)→ 1(3)＞ 3(3)→ 2(3)＞ 2(1)→ 1(1)＞ 105，说明3个异构化反应正向进行反应限度大于逆向且均能正向进行较为完全。同时反应1(1)→1(3)的K值远大于另外两者，说明该反应进行最为彻底。

表2 团簇NiCo2S4异构化反应各项热力学参数Table 2 Thermodynamic parameters of isomerization reaction of cluster NiCo2S4

反应摩尔熵变ΔrSm表明反应前后熵值的变化情况，当ΔrSm＞ 0时，反应物结构有序性强于生成物。1(1)→ 1(3)和 2(1)→ 1(1)的ΔrSm＞ 0，表明上述反应中构型的结构有序性满足 2(1)＞ 1(1)＞ 1(3)；3(3)→ 2(3)的ΔrSm＜ 0，表明结构有序性 3(3)＜ 2(3)。

当ΔrHm＞ 0 时，反应吸热；ΔrHm＜ 0，反应放热。异构化反应的ΔrHm均＜ 0，即所有反应均是放热反应。由价键理论可知，3个异构化反应均是成键放出的热量多于断键吸收的热量。ΔrHm按照大小顺序为 2(1)→ 1(1)＞ 3(3)→ 2(3)＞ 1(1)→ 1(3)，即反应 2(1)→ 1(1)放出的热量最少，反应1(1)→1(3)放出的热量最多，结合上文分析的异构化反应成断键情况可知，3(3)→ 2(3)与 1(1)→ 1(3)的成键数大于断键数，2(1)→ 1(1)成键数少于断键数，说明单纯靠反应前后成断键数量不能决定最终吸放热情况，还需要结合具体成断键种类。综合上述分析和相关内容可知，反应 2(1)→ 1(1)中S4—S5键能大于7根键（Ni1—Co2、Ni1—S5、Co2—S4、Co2—S5、Co2—S6、Co3—S6 和Co2—S7）的键能，说明非金属成键强度强于金属键及金属与非金属键。根据式(8)可知，1(1)→1(3)和2(1)→1(1)在高温条件下更易自发进行且反应更为完全，而3(3)→2(3)在低温条件下更易自发进行且反应更为完全。

2.2.3 团簇NiCo2S4异构化反应相关预测

在上述公式和分析的基础上，可对其余异构化反应进行预测，因此将5个构型进行排列组合，遵循由不稳定构型到稳定构型的原则，在排除已有异构化反应后，对其进行计算处理，并将相关数据和计算结果列于表3。

表3 团簇NiCo2S4异构化反应热力学反应各项参数预测Table 3 Prediction of thermodynamic reaction parameters of isomerization reaction of cluster NiCo2S4

由ΔrGm可知所有异构化反应均能正向自发；2(3)→ 1(3)的K值处于 10-5～105之间，表明该反应不太彻底；除上述反应外其余异构化反应K值均＞ 105，表明这些反应进行较为完全；由ΔrHm均＜ 0可知，所有异构化反应均为放热反应；ΔrSm除反应3(3)→1(3)外其余反应均＞ 0可知，大部分异构化反应均为结构有序性提高的反应。

综合已有和预测的异构化反应的分析情况可得，团簇NiCo2S4异构化反应大都为在高温条件下放热且结构有序性增大的正向可自发反应，K值范围为 28.387～5.461 × 1051。

2.3 团簇NiCo2S4异构化反应的动力学研究

2.3.1 团簇NiCo2S4异构化反应能垒

因化学热力学只能讨论团簇NiCo2S4异构化反应过程的方向与限度，不能考虑反应的难易程度，故用化学动力学对团簇NiCo2S4异构转化进一步分析。同时为直观展现团簇NiCo2S4构型的转化情况，将所有过渡态及对应反应物种的能量值绘制出异构化反应能垒图，如图3所示。

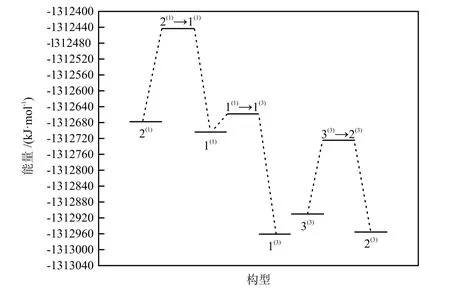
图3 团簇NiCo2S4异构化反应能垒图Fig.3 Energy barrier diagram of isomerization reaction of cluster NiCo2S4

基于过渡态理论，活化能越低，反应速率越大。从图示的3个异构化反应中反应物与过渡态的能量差，即活化能来看，1(1)→1(3)是最容易进行的，反应 2(1)→ 1(1)是最难进行的。在 1(1)→ 1(3)和 2(1)→ 1(1)中，由于构型1(1)分别充当反应物和生成物，因此可将构型1(1)作为为中间产物，使1(1)→1(3)和2(1)→1(1)整合化简成2(1)→1(3)。综合上述分析可知，该反应能否发生的关键在于构型2(1)能否跨越能垒到过渡态TS2(1)→1(1)，即反应 2(1)→ 1(1)是反应 2(1)→ 1(3)的决速步。

2.3.2 团簇NiCo2S4异构化反应各项活化参数

对过渡态与其反应物种的相关能量物理量经过二次处理后得到其反应各项活化值，包括活化能（ΔE≠，kJ/mol）、活化熵（ΔS≠，J/(K·mol)）、活化焓（ΔH≠，kJ/mol）和活化自由能变（ΔG≠，kJ/mol），相关数据如表4所示。正反应活化值（YaF）和逆反应活化值（YaB）计算公式分别如式(9)和式(10)所示。

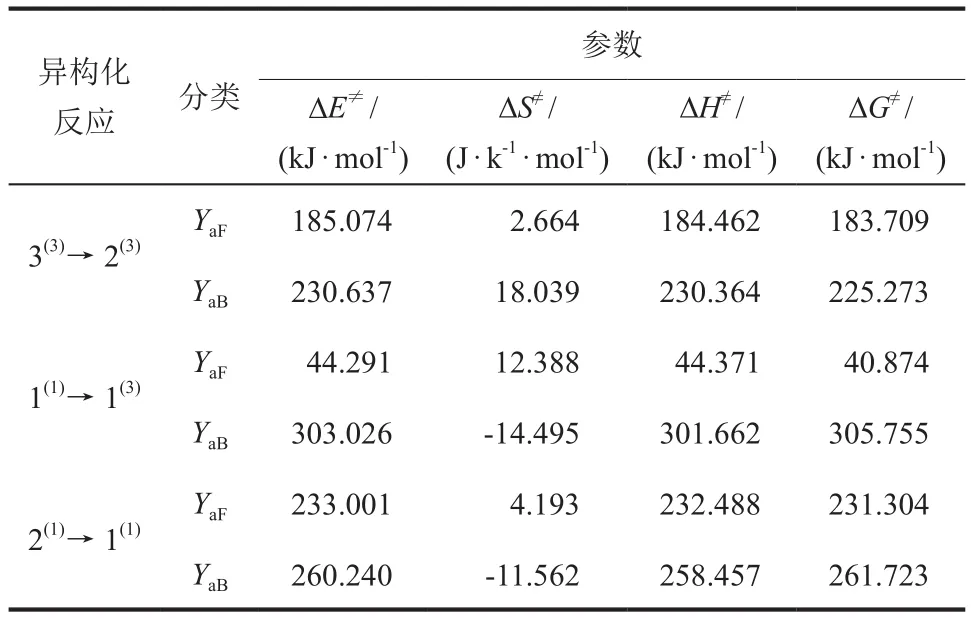
表4 团簇NiCo2S4异构化反应各项活化值Table 4 Activation values of isomerization reaction of cluster NiCo2S4

式中，Y= ΔE≠、ΔS≠、ΔH≠、ΔG≠。

ΔE≠的大小可以衡量反应进行的难易程度，ΔE≠越大，反应越难进行。因此将异构化正逆反应活化能从大到小排序可得：ΔE≠aB(1(1)→ 1(3)) ＞ΔE≠aB(2(1)→ 1(1)) ＞ ΔE≠aF(2(1)→ 1(1)) ＞ ΔE≠aB(3(3)→2(3))＞ ΔE≠aF(3(3)→ 2(3)) ＞ ΔE≠aF(1(1)→1(3))。据此不难发现正向进行的异构化反应中反应1(1)→1(3)最容易发生，反应2(1)→1(1)最难，并且对整体而言，各反应从正向进行比从逆向进行容易。

由过渡态理论和阿伦尼乌斯公式(11)可推导出指前因子A的公式，如式(12)所示。

式中，k为反应速率常数，mol/(L·s)；kB为玻耳兹曼常量，J/K；h为普朗克常数。

由式(12)可以发现A与ΔS≠的变化情况一致，ΔS≠的变化可以表征有关过渡态立体化学特征的相关情况，若ΔS≠＜ 0，则过渡态结构的有序性有所提高；若ΔS≠＞ 0，则有序性降低。1(1)→ 1(3)和 2(1)→ 1(1)的ΔS≠aF＞ 0，ΔS≠aB＜ 0，说明过渡态构型TS1(1)→1(3)和TS2(1)→1(1)的结构有序性高于反应物，但小于生成物。3(3)→ 2(3)的ΔS≠均＞ 0，表明TS1(1)→1(3)结构有序性在反应中最低。ΔH≠由ΔE≠决定，基于过渡态理论中过渡态是反应体系中能量最高的物质，可得ΔE≠＞ 0，反应物到过渡态总为吸热反应，即ΔH≠＞ 0均成立，与表4中的所有异构化反应的ΔH≠＞ 0结果一致。故ΔG≠是否＞ 0，即活化第一步反应是否自发由T和ΔS≠共同影响。当TΔS≠＜ 0时，活化反应一定不能自发进行；当TΔS≠＞ 0 时，根据T、ΔS≠和ΔH≠的相对大小最终确定。根据表4可初步确定常温（298.15 K）时正反应和逆反应的ΔG≠均＞ 0，故所有活化反应均不可自发。

2.3.2 团簇NiCo2S4异构化反应的反应速率常数

前文提及化学动力学中的过渡态理论可以分析反应进行的速率快慢，具体计算公式见式(13)和式(14)。

式中，k(T)为实际速率常数，L/(mol·s)；к(T)为魏格纳校正系数；kTST为理论速率常数，L/(mol·s)；kaF为正反应速率常数，mol/(L·s)；kaB为逆反应速率常数，mol/(L·s)。

由kaF、kaB和K可以计算，结果如表5所示。仅有1(1)→ 1(3)的kaF值＞ 1，其余两个反应kaF值都远远＜ 1，说明 1(1)→ 1(3)中构型 1(1)转化成过渡态的速率最快、所需时间最短，2(1)→ 1(1)中构型 2(1)和 3(3)→ 2(3)中构型3(3)转化速率不甚理想、所需时间很长，不利于实际生产应用； 3(3)→ 2(3)的kaB值最大，1(1)→ 1(3)的kaB值最小，表明 2(3)→ 3(3)进行最快，1(3)→ 1(1)进行最慢。对于平衡常数而言，K＞ 1时，反应实际正向进行速率大于逆向，据此可知所有异构化反应均是正向进行反应。1(1)→1(3)整体表现最为优异，kaF最大，kaB最小，说明反应能快速进行，即构型1(1)不能稳定存在，会迅速转化成稳定构型1(3)。2(1)→1(1)的K值＞ 1，但其数值并不大，可改变反应条件以使其kaF增大或kaB减小。

表5 团簇NiCo2S4异构化反应的反应速率常数Table 5 Reaction rate of isomerization reaction of cluster NiCo2S4

综上所述，对于已存在的3个异构化反应来说，在热力学上和动力学上均可常温下正向自发，具体应用根据实际情况调整反应条件可以使其正向反应自发且平衡速率大。

3 结论

通过采用密度泛函理论和过渡态理论对团簇NiCo2S4优化构型的异构化反应进行了优化计算，得到其过渡态，再结合化学热力学和化学动力学综合分析了优化构型的结构稳定性，得出以下结论。

（1）随着U、H和G的逐渐减小，构型稳定性逐渐降低，生成团簇NiCo2S4时，放出的热量逐渐减少，生成难度逐渐升高。其中构型自旋多重度是引起ΔG发生变化的主要因素之一。

（2）所有异构化反应除2(3)→1(3)外均能较为完全地进行正向反应且均是放热反应，大部分为结构有序性提高的反应。其中1(1)→1(3)反应限度最大，反应进行最为彻底。

（3）构型1(3)是热力学上最稳定的构型，同时在已存在的异构化反应中，构型1(1)可以直接转化为构型1(3)，构型2(1)可以通过转化为构型1(1)间接转化成构型1(3)，因此构型1(3)是团簇NiCo2S4中最稳定的构型，在相关实际实验模型构建中应优先考虑该构型。