基于PSO-SVM的天然气水合物生成条件预测

范 婕，许欣怡，周诗岽，周年勇

（常州大学 石油工程学院 江苏省油气储运技术重点实验室，江苏 常州 213164）

天然气水合物又称笼型水合物，是一种类冰状的结晶物质，由天然气（主要成分为甲烷）和一定量的水在低温高压的条件下形成[1]。作为一种清洁能源，天然气水合物的应用前景十分广阔[2]。然而在天然气集输管道中，天然气水合物的生成会影响输送管线的安全运行。大量生成的天然气水合物在流动过程中会集聚并堵塞管道，导致管内压差增大，严重时会损坏管道[3-4]。为确保天然气在管道中的流动安全，提高天然气水合物生成条件的预测精度是十分有必要的[5]。

在天然气水合物形成条件的预测方面，国内外学者取得了相对丰富的研究成果，形成了以vdW-P模型和Chen-Guo模型[6-7]为代表的热力学计算模型。但在实际过程中，影响天然气水合物生成的因素较为复杂，需要考虑的变量较多，计算复杂繁琐，这限制了纯理论模型的应用。为进一步拓展水合物生成条件的预测方法，REBAI等[8]提出了一种预测混合组分体系水合物生成压力的方法，使用人工神经网络（ANN），对基于vdW-P模型的热力学模型近似地补充了压力修正项，结果显示，压力的总体相对误差从23.75%显著降低到3.15%。SOROUSH等[9]建立了一种前馈式ANN用于预测糖类和酸性气体体系的水合物形成，该模型与其他关联式热力学模型相比，尤其是对混酸气体进行生成预测时，预测精度很高，总均方误差为0.349。MEHRIZADEN[10]采用ANN和自适应神经模糊干扰系统（ANFIS）来估算不同天然气系统的水合物生成压力，将预测结果与实验方程进行比较，结果表明，ANFIS模型在所有情况下都优于ANN模型，且ANFIS模型比经验公式的预测精度更高。郑秋海等[11]通过深度神经网络提取生产数据的网络特征，将提取的特征融合生产数据来增强数据区分度，使用非线性支持向量机（SVM）对融合数据进行水合物生成预测，实验表明深度神经网络结合支持向量机（FDNN-SVM）模型满足海底管线生产运行需求。彭炎等[12]采用支持向量回归方法进行天然气水合物成藏预测研究，结果表明，支持向量回归方法在冻土区天然气水合物生成预测方面的应用是有效的。徐小虎等[13]建立了基于粒子群算法（PSO）的最小二乘支持向量机（LSSVM）模型和误差反向传播（BP）神经网络，对含抑制剂体系下的天然气水合物生成进行了预测，结果表明，前者更为精准。可见，支持向量机能够结合不同的优化算法，对水合物生成预测领域进行研究。

本文针对天然气水合物样本数少这一问题，将粒子群算法结合SVM，选用预测效果好的核函数构建预测模型，预测纯水体系中，纯组分和多组分天然气水合物的生成条件。PSO-SVM模型的输入参数为天然气组分及温度，输出参数为压力。

1 模拟部分

1.1 PSO-SVM模型的算法原理

本文选用SVM和PSO算法建立天然气水合物生成预测模型，并借助MATLAB语言编程实现。实验中能够得到的天然气水合物生成数据并不多，支持小样本数据下的训练预测是SVM的特点之一，因此选用SVM构建天然气水合物生成预测模型。天然气水合物生成数据所绘制的温度压力图是近似平滑的曲线，SVM在曲线拟合方面也较为精准。PSO算法不需要额定的参数，灵活性强，与SVM相结合能解决SVM初始准确度不高和自身学习能力较弱的缺点。

1.1.1 支持向量机

SVM定义最优线性超平面，并把寻找最优线性超平面的算法归纳为求解一个凸规划问题[14]。基于Mercer核展开定理，通过非线性映射Φ，把样本空间映射到一个高维乃至无穷维的特征空间（Hilbert空间），使在特征空间中可以应用线性学习机的方法，解决样本空间中的高度非线性分类和预测等问题[15]。简而言之，就是先将问题升维，然后线性化。SVM是用于分类和回归的算法。天然气水合物生成条件预测是一个低维、非线性问题，本文将对天然气水合物生成条件构建SVM回归预测模型，使其变成能够被解决的高维、线性回归问题。

对于SVM的基本原理，给定训练样本D= {(xi,yi),i= 1, 2, …,N}，xi为自变量，yi为因变量，N为样本量，回归模型如下：

式中，f(x)为模型的输出变量；ω为特征空间权向量；x为输入变量；b为偏置向量。

SVM回归中所使用的结构风险函数表达式如下：

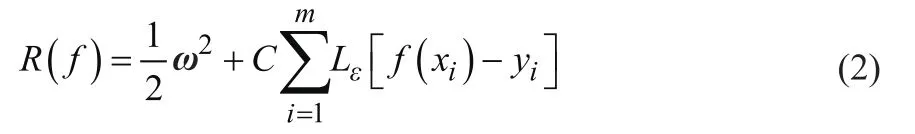
式中，C为惩罚因子；m为样本量；Lε为ε不敏感损失函数；ε为损失函数的损失因子。

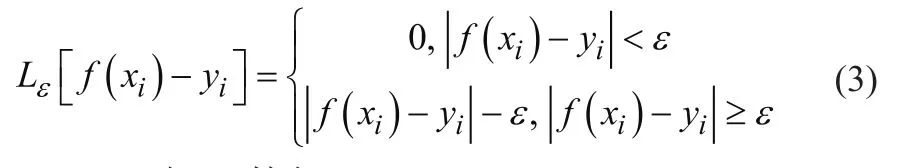
SVM回归函数如下：

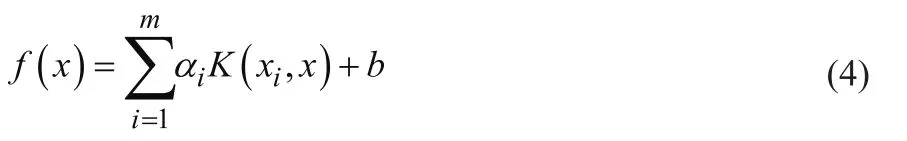
式中，αi为第i个样本的Lagrange乘子，K(xi,x)为内积，即核函数。

对于内积问题，一般会选用性能较好、应用较多的RBF核函数，其表达式如下：

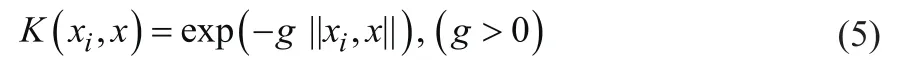
式中，g为核函数的宽度因子。

1.1.2 粒子群算法

PSO是一种进化计算技术[16]，具有容易实现和不需要许多参数调节的特点。这使得PSO能够被广泛地应用到函数优化、神经网络及其参数优化和模糊系统控制等应用领域[17-18]。PSO通过设计一种无质量的例子来模拟鸟群中的鸟，粒子仅具有速度和位置两个属性，用速度体现粒子移动的快慢，用位置体现粒子移动的方向。

粒子通过下式来更新自身的速度和位置：

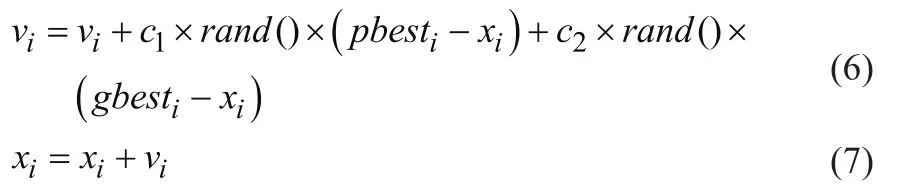
式中，i= 1, 2, …,N，N为此群中粒子的总数；vi为粒子的速度；rand()为介于(0, 1)之间的随机数；pbesti为每个粒子的个体最优值；gbesti为全局粒子的最优值；xi为粒子的当前位置；c1和c2为学习因子，通常取2；vi的最大值为Vmax（大于0），如果vi大于Vmax，则vi= Vmax。

1.1.3 PSO-SVM预测模型的实现方法

管线输送天然气的过程中，天然气中各气体组分含量（物质的量分数）、温度和压力等都是天然气水合物生成的影响因素。将天然气的组分含量、温度作为PSO-SVM模型的变量，将压力作为因变量。为了减少迭代时间，保证算法的高效性，需要对SVM中的惩罚因子C和核函数参数g进行优化。PSO中的个体最优对应SVM中的惩罚因子C，群体最优对应核函数参数g。

本文中PSO-SVM模型的训练过程如下：（1）导入原始数据，按比例随机划分训练集和测试集，同时对数据进行归一化处理；（2）对PSO进行初始化参数设置，将训练集代入到PSO中，结合SVM迭代运算，更新权值，得到两个最优参数惩罚因子C和核函数参数g；（3）将经过PSO计算后的最优参数代入SVM模型中，用测试集进行运算，对得到的数据反归一化；（4）计算实际值与预测值的误差。

1.2 模型的准备工作

1.2.1 实验数据准备及处理

通过调研现有文献[19-22]数据，得到纯水体系下水合物生成数据共132组。其中，纯组分天然气水合物生成数据69组，温度范围273.49～298.20 K，压力范围2.71～43.80 MPa；多组分天然气水合物生成数据 63组，温度范围 273.59～298.00 K，压力范围0.82～24.85 MPa，气体组分如表1。本研究以该数据，建立基于PSO-SVM模型的天然气水合物生成预测模型，并以8:2的比例随机划分训练集和测试集。

对数据进行训练之前，需要先对数据进行归一化处理，使得数据范围稳定，避免存在极端的最大最小值，同时避免数据中的异常值和极端值带来的影响。归一化的效果是将原数据规整到一个闭区间内，通过Mapminmax函数来实现。该程序选用的区间是[1, 2]，即yi∈[0, 1](i= 1, 2, 3, …,N)，这种归一化方式称为[1, 2]区间归一化。所用的归一化映射如下式：

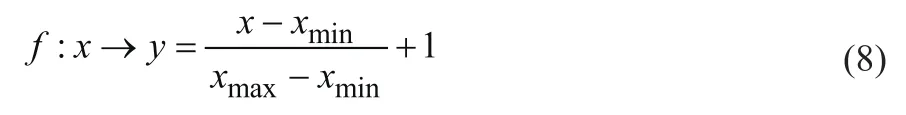
式中，x,y∈R；xmin= min(x)；xmax= max(x)。

1.2.2 SVM模型核函数选取

就SVM中无法处理的非线性可分问题而言，数据需要从低维向高维映射，核函数能够将特征映射到更高维的空间，而计算过程在低维中运行，实际效果表现在高维上，从而解决了维度爆炸的问题。常用的核函数有线性核函数、多项式核函数、Sigmoid核函数和径向基核函数[23]。本文在实际运算过程中，以PSO-SVM模型为基础进行了试算，计算结果见2。由表2可知，径向基核函数的结果最理想，训练集平均平方误差（MSE）和测试集MSE最小，因此选择径向基核函数。

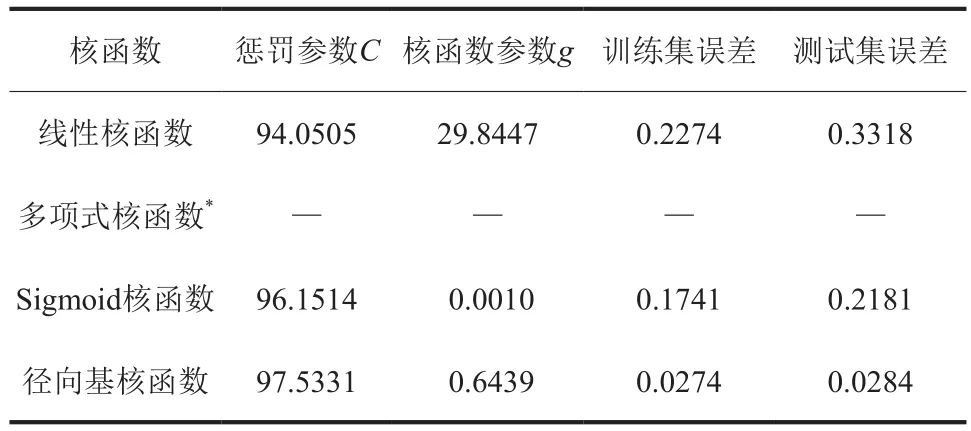
表2 不同核函数下PSO-SVM模型的参数及误差Table 2 Parameters and errors of PSO-SVM model with different kernel functions

1.2.3 运算参数

PSO参数设置对算法本身的运行有很大影响[24]。为进一步研究PSO-SVM模型在天然气水合物生成预测领域中的精准度，对PSO初始化参数进行了优化设计，见表3。PSO-SVM模型运算得到的最优惩罚因子C为97.5331，最优核函数参数g为0.6439。

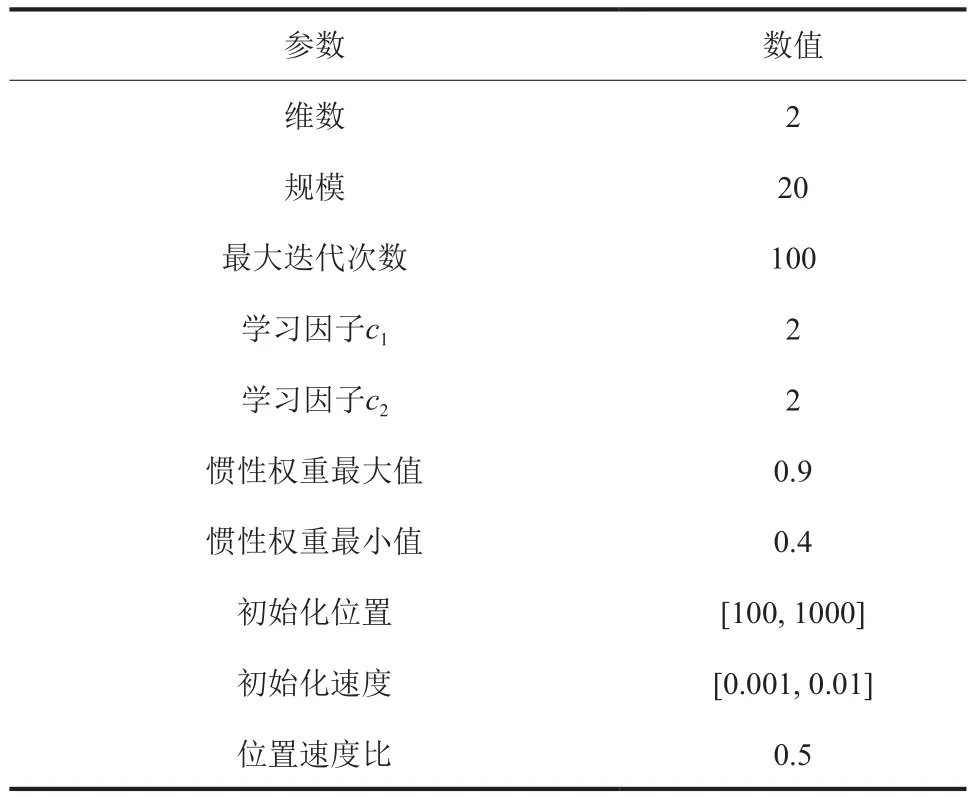
表3 PSO初始参数Table 3 Initial parameters of PSO

2 模拟结果及分析

2.1 不适应度

PSO-SVM模型模拟的适应度较高，所以在程序编写过程中，对适应度的倒数进行曲线描述，如图1所示。由图1可知，随着PSO迭代次数增加，适应度倒数的值越小，该值也指均方差均值，误差越小越好。说明PSO-SVM模型适用于天然气水合物的生成预测。

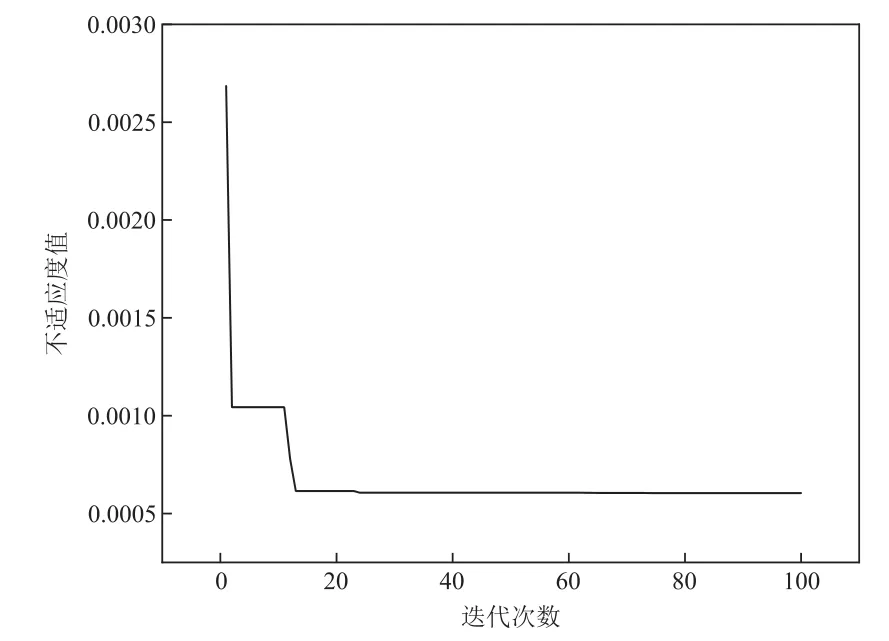
图1 适应度曲线Fig.1 Fitness curve

2.2 纯组分天然气水合物生成预测

通过PSO-SVM模型，对收集到的数据组进行训练预测。纯组分天然气水合物生成预测结果如图2所示。图2中方点代表天然气水合物生成的真实压力，圆点代表PSO-SVM模型计算得到的预测压力。从图2可知，两条曲线的数据点很接近，但在高于295 K后，预测压力误差较大。说明在 273.49～295.00 K之间，PSO-SVM模型预测的可靠性很高，模型相对误差的最大值为8.768%，最小值为0.015%。

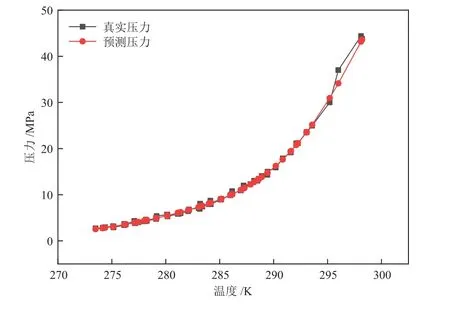
图2 纯组分天然气水合物生成预测Fig.2 Formation prediction of pure component natural gas hydrate

2.3 多组分天然气水合物生成预测

4个不同体系多组分天然气水合物生成预测结果如图3所示。由图3可知，体系1中，两条曲线的数据点基本吻合，个别预测值误差较大；体系2中，数据点在273.80～291.00 K之间的误差较小，但温度高于291 K后，数据的吻合度不高；体系3和体系4中，两条曲线的数据点大体吻合。总的看来，PSO-SVM模型对多组分天然气水合物生成预测的准确度也很高。

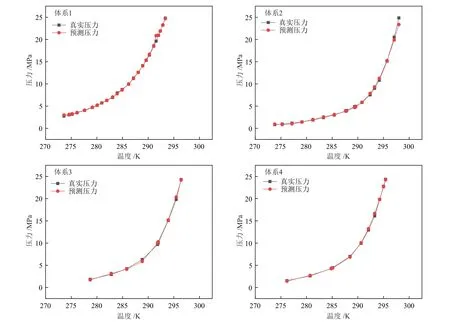
图3 多组分天然气水合物生成预测Fig.3 Formation prediction of multi-component gas hydrate

2.4 PSO-SVM模型误差验证

为进一步检验PSO-SVM模型预测的可行性和准确性，采用MSE、平方相关系数（R2）和平均绝对比例误差（MAPE）等指标进行评价。评价指标定义如下：

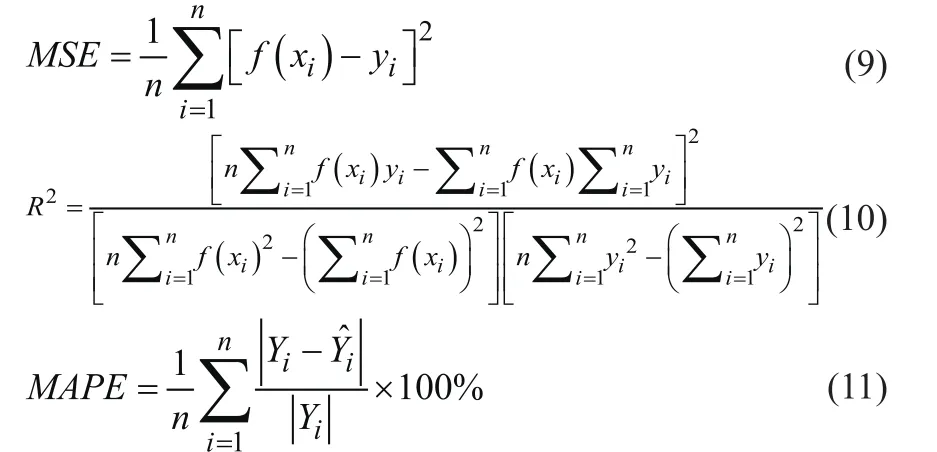
式中，n为样本数；Yi为实际值；为预测值。

MSE为所有样本的样本误差绝对值的均值，该值越接近0，模型越准确；R2为因变量的方差能被自变量解释的程度，该值越接近1，模型效果越好；MAPE为所有样本误差的绝对值占实际值的比值，该值越接近0，模型越准确。PSO-SVM模型对测试集预测的评价结果见表4。

表4 评价结果Table 4 Evaluation results

由表4可知，对于纯组分和多组分天然气水合物，模型的MSE和R2都很理想，并且MAPE也比较低。

3 结论

建立了预测纯组分和多组分天然气水合物生成条件的PSO-SVM模型，并对模型进行了分析与评价，得到如下结论。

（1）SVM的核函数是影响PSO-SVM模型预测结果的主要因素，其中径向基核函数的预测效果最优。预测天然气水合物生成条件，模型最优惩罚因子C为97.5331，最优核函数参数g为0.6439，训练集和测试集的MAPE分别为2.74%和2.84%。

（2）PSO-SVM模型中，纯组分和多组分天然气水合物的适用温度分别为273.49～295.00 K和273.59～298.00 K。

（3）PSO-SVM模型对纯水体系下，纯组分和多组分天然气水合物生成条件具有较好的预测精度，预测纯组分天然气水合物时，MSE、R2和MAPE分别为0.0003963、0.9996和2.84%；预测多组分天然气水合物时，MSE、R2和MAPE分别为 0.0006870、0.9983和2.74%。