基于遗传算法的天然气液化工艺PID控制器参数整定与优化

刘淼儿，单卫光，朱建鲁，刘金华，李恩道

（1.中海石油气电集团有限责任公司，北京 100028；2.中国市政工程华北设计研究总院有限公司合肥分公司，安徽 合肥 230061；3.中国石油大学（华东） 储运与建筑工程学院，山东 青岛 266580）

天然气工业因其清洁、高效和安全等特点在近几十年得到快速发展，开发、利用天然气已成为许多国家实施能源结构调整和可持续发展的重点战略。在近年来提出的“碳中和”目标下，天然气的优势尤为突出。天然气液化技术是液化天然气（LNG）产业链的重要环节，其能耗和控制对产业链的影响巨大，从液化工艺优化、液化装置设计与改进等多方面提高我国天然气领域的相关技术十分必要。而天然气液化工艺是一个多参数耦合的非线性复杂系统，操作运行的稳定性对产品的质量至关重要，因此需要在天然气液化工艺中设置一系列的比例、积分、微分（PID）控制器。

PID控制器逐渐趋向于智能化、自适应化和最优化，目前针对PID控制器的参数整定的主要方法有理论计算整定、工程整定和智能控制[1]。许多学者[2-4]在LNG工业中采用PID控制器控制温度和压力，以改善过程的不稳定性。作为如今工业过程中应用最广泛的控制器，PID控制器仍存在一些待改进的问题，其中最主要的问题是参数整定[5-6]，即确定PID控制器中各环节作用的强弱，如比例参数、积分参数和PID参数的大小，使其在组合后对具体过程有最好的控制效果。

传统PID参数整定通常采取试凑法与经验公式相结合的方式，这种参数整定方法应用于线性控制系统时表现较好，但是在非线性系统控制中的表现不尽人意。在天然气液化工艺中，天然气节流阀的控制器调节就存在控制参数整定困难的问题。随着计算机技术与智能算法的发展，人们开始将遗传算法与PID控制联系起来[7]，遗传算法具备良好的全局寻优能力，且利用遗传算法进行问题优化时，仅用适应度函数来评估个体就可以完成优化过程[8-10]。利用遗传算法的优化作用进行天然气液化动态模型的PID参数整定，目的是寻找PID控制器在具体工作环境下的最佳参数设置，改进控制效果。

本文在天然气液化工艺动态模拟的基础上，结合遗传算法，主要对节流温度串级控制、压缩机压力控制、分离器液位控制等关键控制器的PID参数进行整定和优化，目的是寻找PID控制器在具体工作环境下的最佳参数设置，改进控制效果。

1 遗传算法优化PID控制器参数的方法

1.1 参数整定流程建立

结合已有研究[11-12]，利用遗传算法优化进行PID控制器参数整定的流程如图1所示。其主要流程为：首先采用流程模拟软件和遗传算法工具箱联合的方式，实现天然气液化工艺中PID控制器的参数整定，建立液化工艺的动态模型，便于接下来进行不同PID参数下的动态模拟；其次建立模拟软件与Matlab连接，采用软件的组件对象模型（COM）接口进行调用，利用专用函数抓取工艺流程参数的数据，在天然气液化动态模型PID参数的优化中，将抓取动态模型从加入干扰至恢复稳定过程中的控制变量误差积分值作为适应度函数，并进行接下来的选择、交叉和变异等遗传操作；最后建立遗传算法。

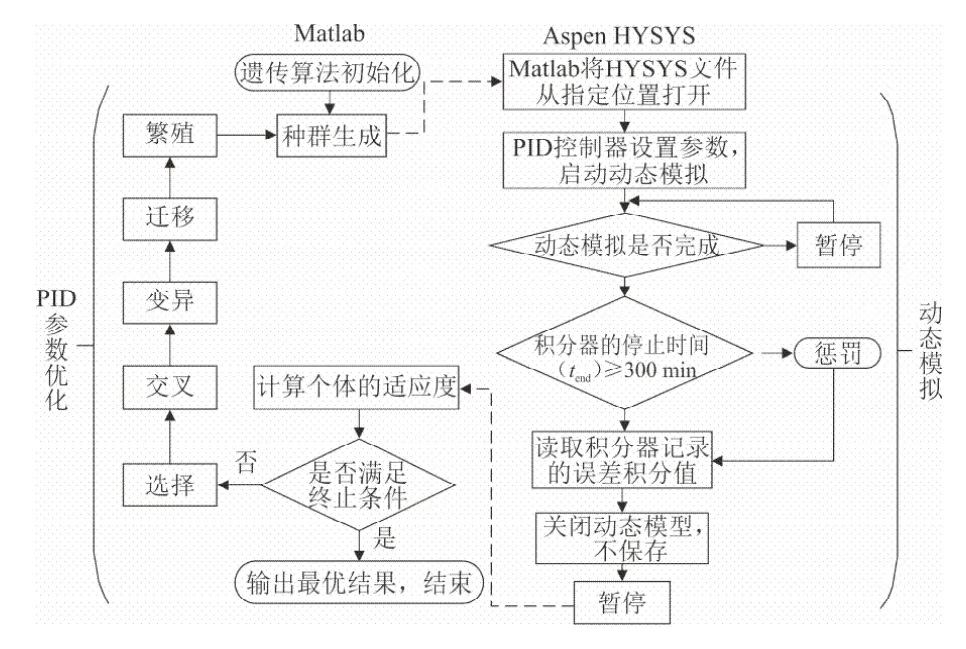
图1 遗传算法优化PID控制器参数的实现过程Fig.1 Realization process of optimizing PID controller parameters by genetic algorithm

1.2 适应度函数的确定

利用遗传算法进行具体问题的优化时，适应度函数的设计是最为关键的一环。优化PID控制器参数的目的是提高动态模型受到干扰后恢复稳定的能力，因此适宜的温度、压力和液位比例、积分和微分参数组合应使系统在受到外界干扰后，系统震荡幅度较小、恢复稳定更迅速。因此，本文采用控制变量的误差对时间的积分值作为评判个体好坏的适应度函数[13]，如式(1)所示。

式中，t1为系统加入扰动时的时间，min；t2为系统恢复至稳定时的时间，min；e(t)为被控变量当前值与设定值间的误差；t为当前时间，min。

偏差（E）的计算如式(2)所示。

式中，Bpv为测量值；Bsp为给定值。

在遗传算法的优化中，个体的适应度值越小，代表其对应的控制器参数的控制效果越好，适应度值小的个体将以更大的概率遗传到下一代[14]。

1.3 约束条件和惩罚函数的确定

为了确定个体的适应度值，需要向天然气液化工艺动态模型中加入干扰并展开动态模拟。在遗传算法的优化过程中，难免会产生控制效果较差的参数组合。当控制器的参数取值不当时，动态模拟有可能出现提前停止的情况，此时动态模拟中的积分器也将提前停止工作。因此，将动态模拟中积分器的停止时间作为约束。若动态模拟积分器的停止时间小于规定值，则对该PID控制器参数对应的种群个体进行惩罚。

在HYSYS的动态模拟中，当控制器参数选择不合理导致控制变量出现发散时，积分器可能提前停止工作，无法得到完整的控制变量响应曲线，因此将tend≥ 300 min作为约束条件。当不满足约束条件时，惩罚函数如式(3)所示。

2 液化装置及数学模型

2.1 液化装置介绍

混合制冷剂液化装置和流程如图2所示，包括制冷剂循环和原料气流程。在本工艺系统中，可以采用对节流温度串级控制、压缩机压力控制和分离器液位控制的控制方式，但是这些控制方式针对不同的适用条件和环境，当需要改变控制的设定值来对工艺系统进行调节时，控制的稳定性和响应速度对整个液化工艺有重大影响，所以需要对其进行动态仿真[15-19]。

图2 混合制冷剂液化装置和流程Fig.2 Liquefaction devices and flow of mixed refrigerant

预冷循环中，预冷制冷剂先进入入口缓冲罐，经两级压缩后进入出口缓冲罐，冷却后形成气液两相，均进入预冷换热器1中。液相的预冷制冷剂经过预冷换热器1冷却，节流后与回流的气相预冷制冷剂共同回流进入预冷换热器1中，作为冷源提供冷量。深冷循环中，深冷制冷剂先进入入口缓冲罐，经两级压缩后依次经过预冷换热器1和预冷换热器2，经预冷换热器2的深冷制冷剂经过气液分离器分为气液两相。液相的深冷制冷剂经过深冷换热器1冷却，节流后与回流的气相深冷制冷剂共同回流进入深冷换热器1中，作为冷源提供冷量。原料气流程中，原料气依次经过预冷换热器1、预冷换热器2和深冷换热器1、深冷换热器2，被降温、液化和过冷形成LNG。

液化装置的主要控制方案包括：压缩机控制、冷剂节流控制和LNG节流控制。压缩机控制为压缩机入口压力调节，通过调节压缩机旁通回流管线上的气动阀，调节压缩机入口压力，当入口压力过高时调小气动阀开度，压力下降，当入口压力过低时增大气动阀开度，压力升高。冷剂节流控制包括：（1）预冷冷剂一级节流，预冷压缩机后缓冲罐液位联锁控制，以预冷冷剂出换热器温度为主环，一级节流前流量为副环的串级控制；（2）预冷冷剂二级节流，以预冷冷剂二级节流前温度为主环，二级节流前流量为副环的串级控制；（3）深冷冷剂一级节流，以深冷分离器液位为主环，一级节流前流量为副环的串级控制；（4）深冷冷剂二级节流，以二级节流前温度为主环，二级节流前流量为副环的串级控制。LNG节流控制以节流前温度为主环，进冷箱原料气流量为副环的串级控制。

2.2 数学模型建立

压缩机是石油、天然气加工等化工行业中的重要设备，用于提高气相物流的压力，适用于处理量较大和压缩比较低的场景。相对于液化流程中其他设备，如换热器、储罐等，压缩机的动态响应比较迅速，因此可以按照稳态模型来近似处理来简化压缩机模型。天然气液化流程中，节流过程与外界的换热可以忽略不计。将板翅式换热器的动态模型简化为一维模型：流体在垂直于流动方向的性质均匀，每股流道内的换热系数不变，流道内的压降为流量的函数，两相流动过程中，气、液的流速相同，忽略换热器的热损失，忽略流体以及换热器隔板的纵向导热。设备的数学模型如表1所示。

表1 设备数学模型Table 1 Mathematical models of equipment

3 天然气液化工艺PID控制器参数优化

3.1 LNG节流温度的串级控制分析

在天然气液化工艺中，为了保证LNG的流量，采用串级控制方案调节节流前的天然气温度，该处的串级控制包括流量控制器和温度控制器。其中，LNG温度控制作为串级控制器的主环，原料气的流量控制作为串级控制的副环。温度控制器对节流前天然气的温度进行检测，然后对流量控制器的设定值进行调节，从而改变原料气的流量，两个控制器的共同作用使节流前的天然气温度保持稳定。天然气节流温度串级控制动态模拟如图2所示，为了对比PID控制器在经验整定与遗传算法优化整定下的控制效果，在稳定运行的天然气节流温度串级控制动态模型中加入原料气压力扰动，记录动态模型在不同控制器参数下的控制效果。动态模型稳定运行时，原料气压力为3900 kPa，节流前的天然气温度稳定在设定值-157.6 ℃。动态模拟开始后，原料气的压力随时间作正弦波动，如式(4)所示。

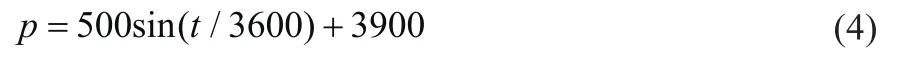
设置优化变量及其上、下限，天然气节流温度串级控制中有温度和流量两个控制器，在HYSYS的动态模拟中，天然气节流温度的控制效果主要取决于控制器的增益和积分时间常数，而微分时间常数的加入不能有效改善控制效果。因此，本文分别将温度控制器和流量控制器的增益和积分时间常数作为优化变量，并利用遗传算法寻优，变量的优化范围如表2所示。

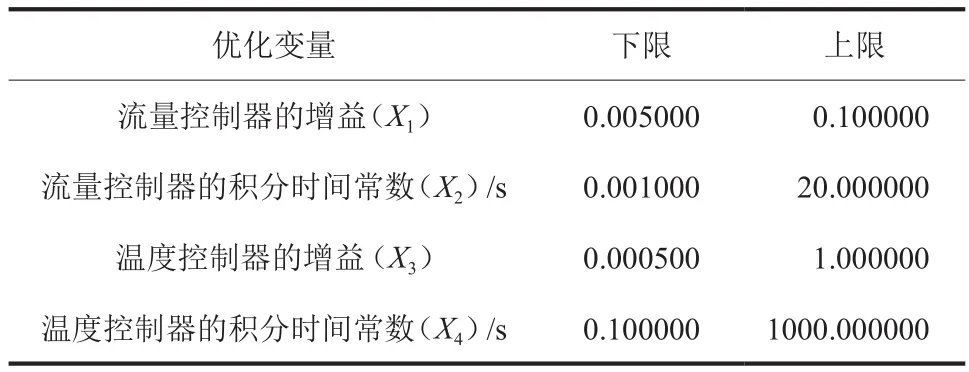
表2 变量的优化范围Table 2 Optimization range of variables

使用式(1)作为适应度函数进行遗传算法优化求解，遗传算法优化迭代曲线如图3(a)所示。优化进行到第118代时结束，得出最优个体对应的变量值。根据优化结果设置控制器参数，进行动态模拟，并与经验整定的参数进行控制效果对比，结果如图3(b)所示。

图3 LNG节流温度的串级控制结果Fig.3 Cascade control results of LNG throttling temperature

根据经验整定和遗传算法优化整定得到的LNG节流温度串级控制的控制器参数以及在动态模型恢复稳定的过程中，两种控制器参数对应的节流温度误差积分值如表3所示。改变原料气的压力后，由于换热过程的影响，节流前的天然气温度滞后约8 min开始升高。天然气节流温度控制动态模型的PID控制器参数在进行遗传算法优化后，温度控制过程累计误差降低了17.7%，控制效果得到了改善。

表3 不同方法下的控制器及温度误差积分参数Table 3 Controller and temperature error integral parameters under different methods

3.2 压缩机出口压力控制分析

二级压缩机出口压力控制动态模拟如图2所示，压力控制器通过控制节流阀的开度来调节气相制冷剂的回流流量，从而调节二级压缩机的出口压力。为了对比PID控制器在经验整定与遗传算法优化整定的控制效果，展开动态模拟对比，将进气缓冲罐入口的混合制冷剂压力作为扰动，记录动态模型在不同控制器参数下的压力控制效果。其中，进气缓冲罐入口的混合制冷剂压力随时间作正弦波动，如式(5)所示。未加入扰动前，进气缓冲罐入口的冷剂的压力为950 kPa，二级压缩机的出口压力稳定在设定值 1700 kPa。

在压缩机出口压力控制的HYSYS动态模拟中，压缩机出口压力的控制滞后性很小，控制效果主要取决于控制器的增益和积分时间常数，因此，将压力控制器增益（X5，上限和下限分别为5.000000和0.000000）和积分时间常数（X6，上限和下限分别为5.000000 s和 0.100000 s）作为优化变量。使用式(1)作为适应度函数进行遗传算法优化求解，得到的迭代曲线如图4(a)所示。经遗传算法优化迭代到第117代时，得到了最优个体，其代表的控制器参数具有在设定扰动下的最佳压缩机出口压力控制效果，两种方法对控制器参数的控制效果对比如图4(b)所示。

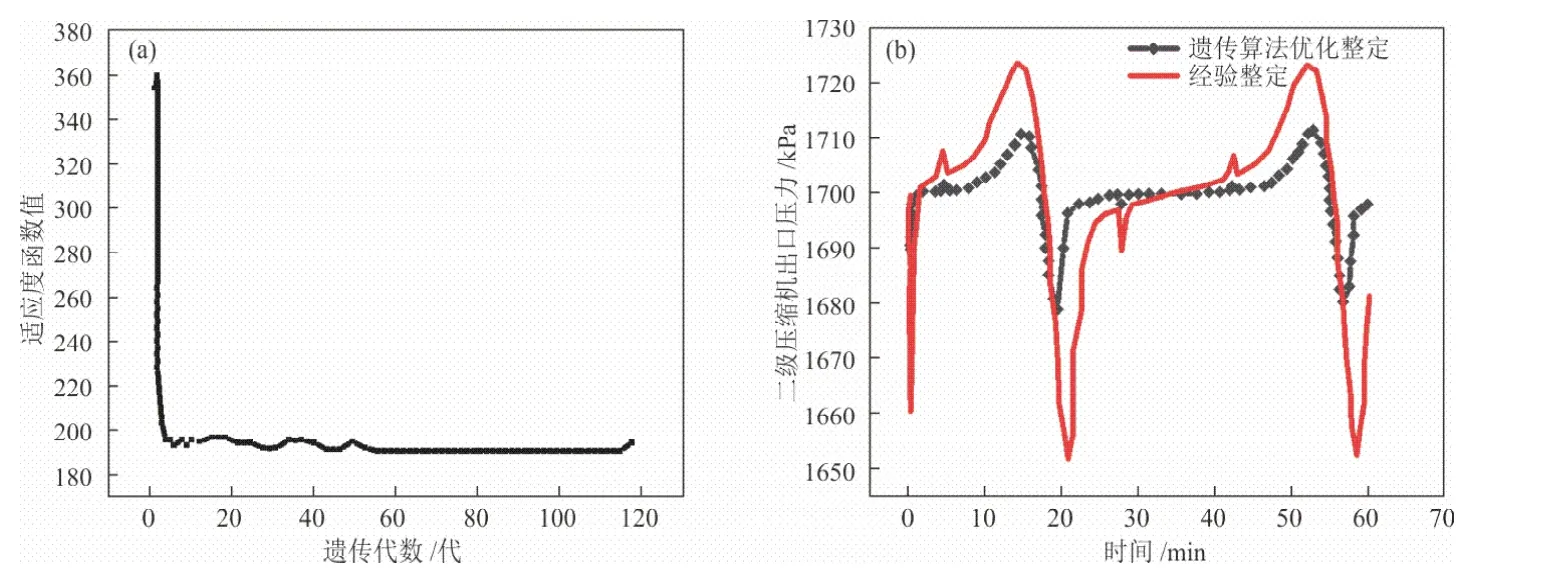
图4 压缩机出口压力控制结果Fig.4 Control results of compressor outlet pressure

根据经验整定和遗传算法优化整定得到的二级压缩机出口压力控制器参数以及压力控制过程中，两种控制器参数整定方案对应的压力误差积分值如表4所示。二级压缩机出口压力控制动态模型的PID控制器参数在进行遗传算法优化后，压力控制累计误差降低了71.4%，控制效果得到了改善。

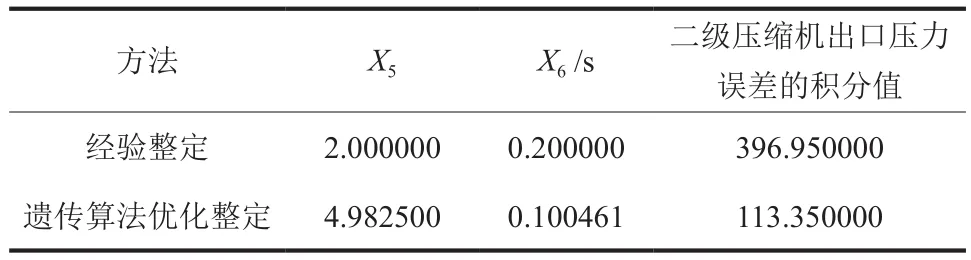
表4 不同方法下的控制器及压力误差积分参数Table 4 Controller and pressure error integral parameters under different methods

3.3 混合制冷剂液位控制分析

混合制冷剂液位控制动态模拟如图2所示，液位控制器检测分离器中的液位，通过调节液相制冷剂回路中的节流阀开度来调节液相制冷剂的流量，从而使分离器中的液位稳定在设定液位上。为了对比PID控制器在经验整定与遗传算法优化整定下的控制效果，展开动态模拟对比，将分离器入口的混合制冷剂压力作为扰动，记录动态模型在不同控制器参数下的压力控制效果。其中，分离器入口的混合制冷剂压力随时间作正弦波动，如式(7)所示，未加入扰动前，分离器入口的混合制冷剂压力为2000 kPa，分离器中的液位稳定在设定值的50%。在HYSYS的动态模拟中，分离器液位控制的控制效果主要取决于液位控制器的增益和积分时间常数，因此，将液位控制器的增益（X7，上限和下限分别为10.000000和 1.000000）和积分时间常数（X8，上限和下限分别为 100.000000 s和 1.000000 s）作为优化变量，进行遗传算法寻优。

使用式(1)作为适应度函数进行遗传算法优化求解，得到的迭代曲线如图5(a)所示。经遗传算法优化迭代到第105代时，得到了最优个体，对应的最优变量值即为遗传算法优化后的增益与积分时间常数。对比两种参数，展开动态模拟，两种控制器参数整定方案对应的液位控制效果如图5(b)所示。

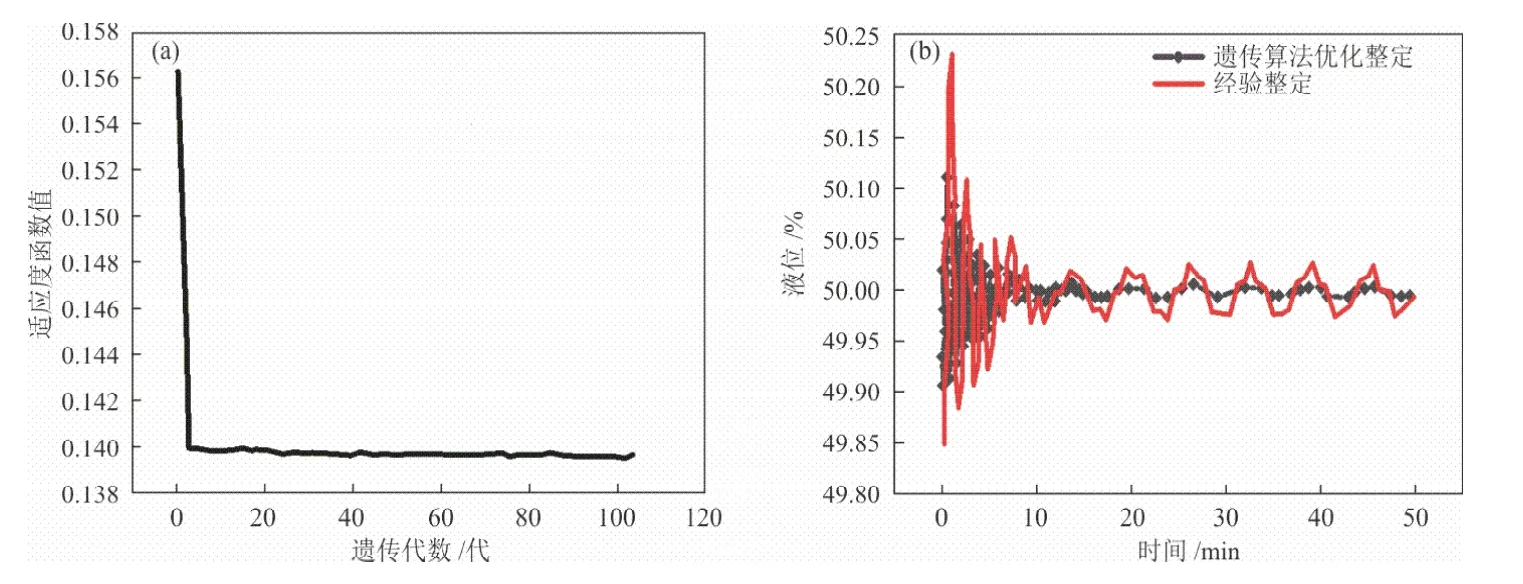
图5 混合制冷剂液位控制结果Fig.5 Control results of mixed refrigerant liquid level

经验整定和遗传算法优化整定下的分离器液位控制器参数设置以及在液位控制动态模型恢复稳定的过程中，两种控制器参数对应的液位误差积分值如表5所示。相对于经验整定，通过遗传算法优化得到的控制器参数改进了分离器液位控制的控制效果。混合制冷剂液位控制动态模型的PID控制器参数在进行遗传算法优化后，液位控制累计误差降低了92.9%，控制效果得到了改善。

表5 不同方法下的控制器及液位误差积分参数Table 5 Controller and liquid level error integral parameters under different methods

4 结论

本文针对天然气液化工艺控制问题，建立了液化装置与数学模型，将动态模拟中积分器的停止时间作为约束，以累计误差作为目标，对基于遗传算法理论的PID控制器参数整定的方法进行了研究，得到以下结论。

（1）采用串级控制方案调节节流前的温度，利用遗传算法进行了天然气节流温度控制，优化整定积分时间常数和温度控制器增益，优化后的结果分别为 11.990380 s和 908.078200 ，温度控制过程累计误差降低了17.7%。

（2）对压缩机出口压力分析，将进气缓冲罐入口的混合制冷剂压力作为扰动，利用遗传算法优化整定积分时间常数和压力控制器增益，优化后的结果分别为0.100461 s和4.982500，与经验整定方法控制效果相比，压缩机出口压力累计误差降低了71.4%。

（3）对混合制冷剂液位控制分析，将分离器入口的混合制冷剂压力作为扰动，利用遗传算法优化整定积分时间常数和液位控制器增益，优化后的结果分别为1.031654 s和9.998923，与经验整定方法控制效果相比，优化后混合制冷剂液位控制累计误差降低了92.9%。

本文的研究方法可以为实际天然气液化装置的稳定运行提供指导，提高控制精度、缩短稳定时间，同时在设计阶段，通过天然气液化工艺的动态仿真，开展不同工况的运行校核，可提前模拟并预测控制系统的可靠性，为设计参数选择和余量确定提供依据。